一种刚柔耦合变径操作臂的建模和性能分析

姜晓勇 , 黄朗月, 彭孟乐, 李忠义

(1.浙江科技学院 机械与能源工程学院,杭州 310023,E-mail:119082@zust.edu.cn;2.浙江省智能运维机器人重点实验室 ,杭州 311100)

近年来,机械臂在各种工业领域应用越来越广泛,现代工程应用型连续操作机械臂多以关节串联衍生出来。连续性操作机械臂的灵感大多来自于如蛇,水蛭等无脊椎生物[1-3]。柔性连续体操作臂主要是由一些弹性材料构成其主要结构,按驱动方式主要可以分为软体气动型、线控型、记忆金属型和人工肌肉型。但随着操作臂的工作空间和作业方式越来越复杂,单一的柔性连续性操作臂已经不能满足需要,为了提高其工作性能,混合型的柔性操作臂逐渐出现,面向不同应用场景的柔性操作臂也越来越多样化。

范德堡大学的Nabil Simaan和徐凯等人提出了一种以杆型连续体结构为基础的喉部手术机器人[4],该机器人作为医疗手术机器人其结构尺寸精小,长度约为32 mm,直径为5 mm,四根弹性镍合金杆构成其主要结构,其主承受杆为固定长度的弹性中心杆件,另外可变长度的三杆均匀分布于中心杆的四周。弹性中心杆的变形由其他三杆约束,通过改变外围均匀分布的三根弹性杆的长度,该机器人可完成弯曲和旋转运动,并通过前端的微型金属钳进行手术操作[5-6]。

香港中文大学的李铮等人提出了球形关节结构的软索驱动连续体机器人[7-8]。该结构的灵感来自蛇的骨骼和章鱼触手,该机器人由三个相同结构的单段柔性连续体组成,每一单段由多个球形关节和中心弹性杆组成。每段连续体机器人由两组导线驱动,该设计将蛇形机器人的结构与连续机器人的驱动相结合。

德国汉诺威大学的Thien-Dang Nguyen等人提出了具有伸缩功能的弹性磁结构,并将自由度提升,形成可伸缩的柔性连续体机器人[9]。该机器人除了通过软索驱动进行弯曲外,可伸缩弹性杆还允许其在运动中调整各约束节片之间长度。因此,机器人整体的长度是可变的,弯曲半径的范围也可以随之扩大。该机器人的约束节片与一般的不同,每个约束节片带有交替磁极方向永磁体,利用磁体的排斥力,使柔性连续体机器人在任意长度上具有等距间距性。

英国诺丁汉大学的XinDong 等人将多段串联,形成更高自由度的连续体机器人[10]。随后改进使其拥有了更高的自由度,该机器人主要服务于工业狭窄环境的勘探和护理工作,如对飞机引擎的维护和修复工作。在进一步的研究中,其更高的自由度在带来更好的灵活性的同时,也使其控制难度加大。

研究发现,在柔性操作臂的研究中,线控相比于杆控的控制精度相对较低,杆控虽然精度较高但是其控制策略往往难于线控,而本研究将线控和杆控相结合,以线控作为主要的控制策略,杆控作为被动控制用于提高整个操作臂的精度,本研究中的新型刚柔耦合变径操作臂基于其变刚度、变直径,线控、杆控相结合的特征,结构轻便,能满足如四足机器人作为载体时搭载该操作臂进行作业的应用场景[11-13]。

1 操作器的功能原理

1.1 结构

本文中介绍的刚柔耦合变径操作臂其结构主要是由四个基本刚性伸缩骨架构成,由十字轴将四个单位骨架连接起来。如图1所示。

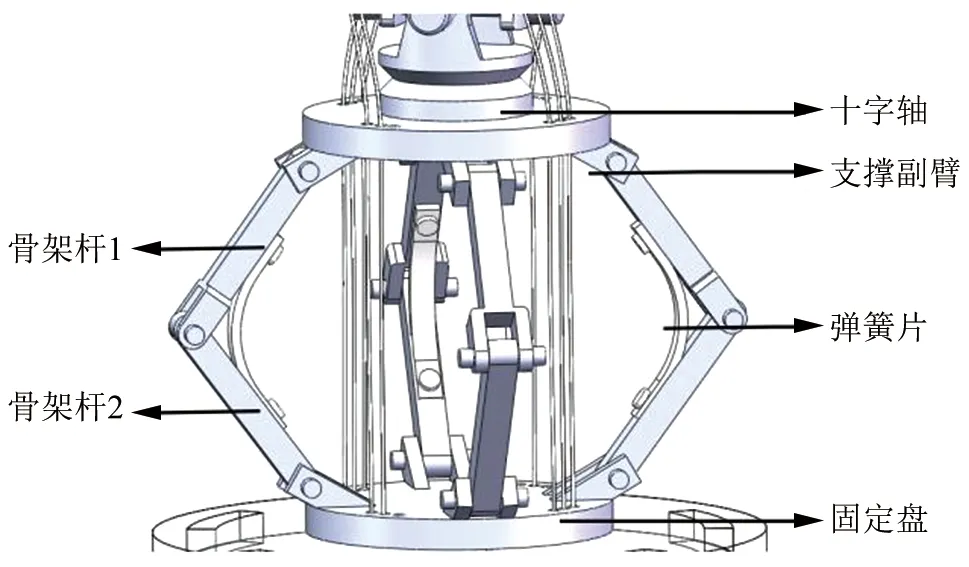
▲图1 单位骨架结构图

该变径操作臂的每一个单位骨架由4根骨架杆1和骨架杆2以及两个固定盘组成,每一个单位骨架是一个对称型结构,8根骨架杆分别位于两个固定盘上间隔90°对称铰接,在对称的两骨架杆之间的铰接处安装一个弹簧片作为骨架变直径支撑机构,一个单位骨架一共装有4个弹簧片。十字轴分别连接在第N个骨架和第N+1个骨架的首尾固定盘上,本研究中用3个十字轴将4个单位骨架连接在一起。每一个单位骨架的固定盘上有间隔均匀的四个小孔用于穿过钢丝绳对操作臂进行控制[14]。其中单位骨架作为新型刚柔耦合变径操作臂的主要结构,可改变操作臂的形状和直径大小。

刚柔耦合变径操作臂的固定盘的直径为50 mm,骨架杆长度为38 mm,两骨架杆之间的角度变化范围为53.13°～180°,其两杆之间的夹角范围可根据操作臂的作业环境和作业所需刚度进行改变。本文以此数据为例对操作臂进行设计和建模。

1.2 工作原理

▲图2 弯曲角度控制图

本文中,对刚柔耦合变径操作臂设计了控制策略,可以实现操作臂的弯曲,伸缩,变直径,变刚度等。操作臂的每一个单元体都可以实现不同角度的弯曲,这种不同角度的弯曲由不同位置的线控单元决定[15]。如图2所示,操作臂的弯曲由四个线控单元进行控制,根据上一节设计,四条钢丝绳均匀穿过每一个单元骨架体的支撑盘将四个单元骨架连接起来,当不同的线控单元被激活时,就会引起各单位骨架之间不同的弯曲角度。

操作臂的变直径运动由一个线控单元实现,两条钢丝绳间隔180°穿过各单位骨架的支撑盘,最终每个单位骨架的钢丝绳都由同一个交流电机进行控制以此实现每一个单位骨架具有相同直径。

在每一个单元骨架上均装有4个弹簧片,通过变径线控单元将各单位骨架拉伸到所需的直径,此时弹簧片被压缩,对于单位骨架而言弹簧片产生一个与线控单元相反的力,以此来保证各单位骨架的稳定性和刚度,进而实现单位骨架的伸缩以达到改变整个操作臂的直径、长度和刚度的目的。当各控制单元协同控制时,能使得各单位骨架组成的操作臂到达不同的工作位置。

2 建模分析

本文中所述的可变刚度的柔性操作臂能提供了Z轴方向移动的自由度,因此将整个操作臂的工作空间不再是二维曲面,而是三维空间。操作臂的姿态由固定盘上的五组线控单元决定,其中固定盘四周的四组线控单元是控制了操作臂X轴和Y轴上的转动,所以本文的分析将单位骨架之间的弹簧模型简化为十字轴模型[16]。传统的D-H系分析方法仅适用于刚性机械臂的分析,在本文中提出的D-H-Φ方法引入一个新的参数Φ,定义为操作臂每一个关节处的偏转方向。如图5示建立基架O-XYZ,将Φ定义为操作臂每一单位骨架中心轴线在平面XOY中投影线与Y轴在X轴正方向上的夹角。

2.1 变直径分析

本文中所研究的刚柔耦合变径操作臂是由单位骨架作为主体的,其中单位骨架的直径大小决定了整个操作臂的直径大小。以其中一个单位骨架为例,由于其单位骨架的对称性,所以在对其进行最大最小直径分析时将其简化为一个二维平面分析。简化模型图如图3所示,其中固定盘半径R1=25 mm,支撑副臂d=5 mm,骨架杆1和骨架杆2长l=32 mm,γ=60°,骨架杆厚度a=2.5 mm,α、β、h、Δ如图所示。

▲图3 变径分析模型简化图

由于操作臂的最小直径由单位骨架的骨架杆1和骨架杆2之间的铰接角度决定,根据本文中所述的刚柔耦合变径操作臂的结构设计,骨架杆1和骨架杆2之间的最大铰接角为120°,且单位骨架的轴长为h,此时单位骨架支撑盘的半径及其副臂所决定。在本文中,将操作臂的直径分析分为三个部分,分别为x1、x2、x3:

(1)

式中:β角随着操作比弯曲程度的变化而变化,通过对图3中模型的分析可得:

(2)

当β=60°时cosβ最小,当Δ=5mm时cosβ最大。

(3)

2.2 运动学分析

如图4所示,本研究中十字轴的尺寸为h1=18.22 mm。

根据图1单位骨架结构图可知单位骨架的轴长L表示为:

L=2(dcosγ+lsinβ)+h1

(4)

▲图4 十字轴

本文的研究中操作臂远端位姿可用参数ai、∂i、di、θi、Φ描述。如图5示建立基O-XYZ,以第一单位骨架的一个支撑盘的几何中心作为原点,以支撑盘的轴心线作为Z轴,X、Y轴方向如图5所示。

▲图5 基架简化图

由于在每一个单位骨架之间有十字轴连接,所以将模型近似简化为如上图4所示的空间基架简化图。因为每一个单位骨架与十字轴之间为刚性连接,所以十字轴的尺寸h1做为单位骨架的一部分,即将每一节单位骨架轴长由单位骨架本身的轴长和固定的刚性十字轴尺寸之和决定。将两个十字轴之间的距离定义为σ,根据操作臂三维建模尺寸可知σ趋向于零。建立运动学模型参数表1如下[17]:

表1 运动学模型参数表

在D-H系坐标中ai是连杆i的运动长度,即在xi-1方向上zi-1轴与zi轴之间的距离;∂i是连杆扭转角,即在xi-1轴方向上zi-1轴与zi轴之间的夹角;di是关节距离,即zi方向上xi-1轴与xi轴之间的距离;θi是在zi轴方向上xi-1轴与xi轴之间的夹角。

基于D-H-Φ分析法的规定,将相邻坐标系Bi变换至坐标系Bi-1的变换矩阵i-1Ti可以用连杆i和关节i的4个基本变换乘积表示,即:

i-1Ti=(DZi-1,di)(RZi-1,θi)(DXi-1,ai)(RXi-1,∂i)=

(5)

则从Bi(xi,yi,zi)变换到Bi-1(xi-1,yi-1,zi-1)的变换方程为:

(6)

由公式(5)可知:

(7)

(8)

(9)

(10)

(11)

(12)

在本文中,一共有6个相对坐标系,即产生6个相对变换矩阵,按照D-H系坐标分析方法,即操作臂最后的末端位置由上述6个相对变换矩阵决定:

0T6=0T1×1T2×2T3×3T4×4T5×5T6

(13)

即得到操作臂末端位置相对于基架O-XYZ坐标系的变换矩阵0T6。

由公式(6)可得:

(14)

综上所述,根据公式(14)可得到操作臂末端的位置,操作臂末端位置与单位骨架的单位轴长有关,还与每一个单位骨架之间的十字轴之间的运动角度有关。操作臂末端位置的集合就是操作臂的工作空间。

2.3 动力学分析

本文中对操作臂进行动力学分析主要是为了分析操作臂的末端位置随时间变化时末端加速度的变化,根据图5基架简化图对操作臂进行分析。

将操作臂放在坐标系i和i+1中进行分析,操作臂在坐标系i运动时,在坐标系i+1中会产生一个相对的牵连加速度,即坐标系i+1相对于坐标系i的速度i+1vi,i+1wi:

(15)

式中:ipi+1表示坐标系i+1相对于坐标系i的位置向量,iwi,ivi分别表示在坐标系i中操作臂的线速度和角速度,iRi+1表示相邻坐标系Bi+1变换至坐标系Bi的旋转矩阵。

则根据上一节的运动学分析可知旋转矩阵为:0R1、1R2、2R3、3R4、4R5、5R6,操作臂的初始状态为0w0=0,0v0=0,σ表示十字轴两轴之间的距离,所以σ→0则有:

将每一个坐标系的相对线速度和角速度表示如下:

(16)

综上,根据此迭代法最终迭代出6w6,6v6。

因为vi=0vi=0R11R2.....i-1Riivi,得出:

…………
v6=0R11R22R33R44R55R66v6

(17)

本文研究中对从操作臂的动力学分析采用牛顿法分析,即:

对杆件进行分析:

(18)

式中:F1是驱动第一臂所需动力,即为驱动器所需动力[18-19]。在动力学分析中,将操作臂的力与运动相结合,可以得出,驱动器所需力与操作臂的直径之间受Δ影响,根据此动力学模型即可得出操作臂的工作空间位置与驱动器所需力的关系。

3 技术性能分析

本研究中所建立的刚柔耦合变径操作臂具有7个输入变量,分别为:θ1、θ2、θ3、θ4、θ5、θ6、Δ。文中的刚柔耦合变径操作臂作为一个研究模型,其输入参数范围可根据不同的工作要求进行设计,以满足不同的应用场景。

由上一节中,L=2(dcosγ+lsinβ)+h1,Δ的取值范围在2.886 mm～5 mm,则L的取值范围为55.22 mm～78.644 mm。

在本研究中θ1、θ2、θ3、θ4、θ5、θ6、Δ作为输入变量,操作臂的末端位置为输出,操作臂的控制约束条件根据不同影响因子进行不同的分析,下面将操作臂的影响因子分为两大类型进行约束实验。本研究中操作臂受θi、Δ变量所影响,将对操作臂进行可达到工作空间的分析以及驱动操作臂所需力矩的分析。

3.1 工作空间分析

3.1.1θi对工作空间的影响

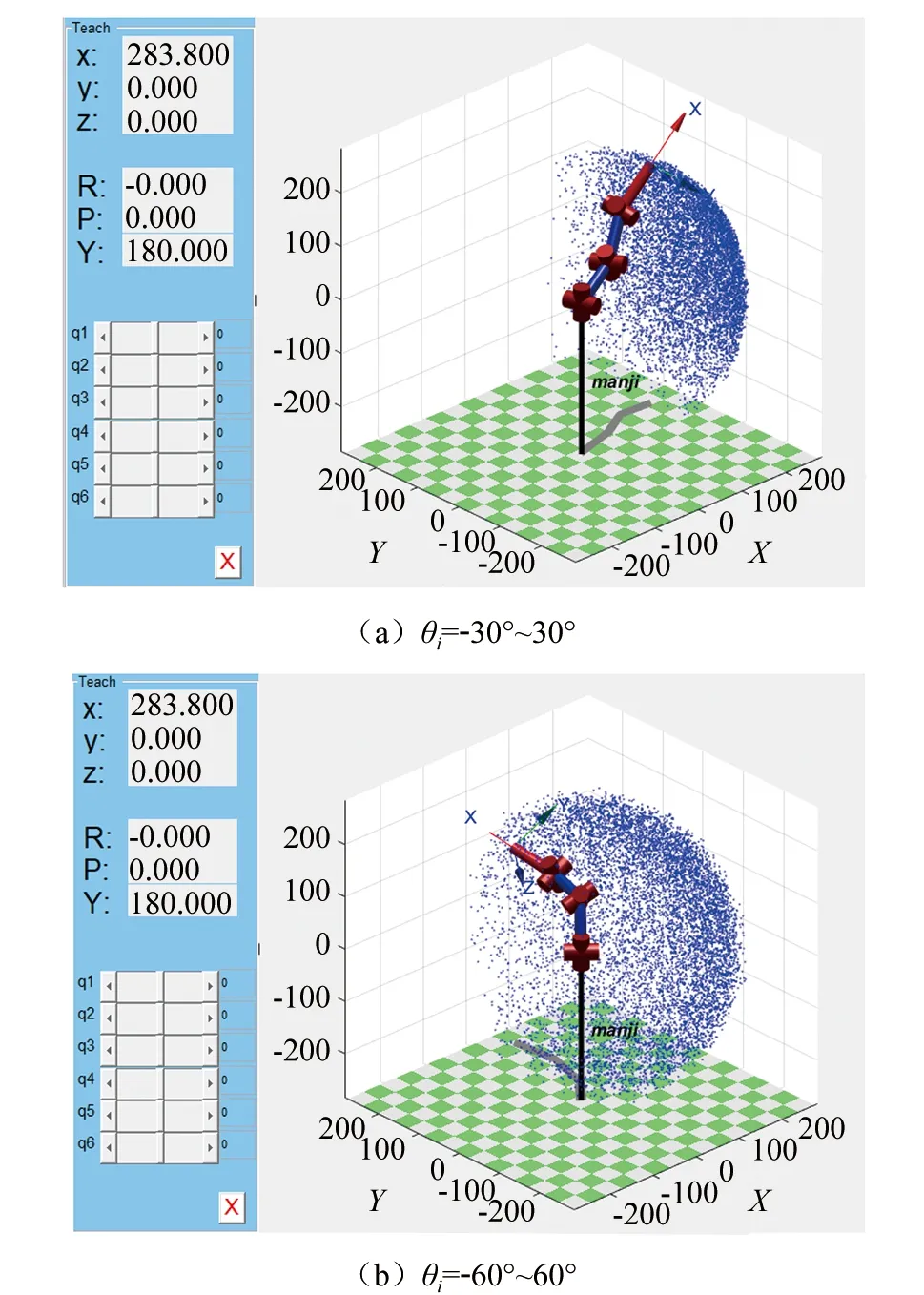
▲图6 工作空间中位置状态结果

其中空间点云图表示操作臂在空间中任意的位置点,将空间位置点图对应的空间位置坐标图在坐标系中,由于在本组实验中取Δ=0,L=82.22为定值,所以操作臂的长度为一定值,由于其工作空间时以原点为球心,操作臂长度为半径的球的弧面,所以θi的取值范围决定了操作臂的转动范围即决定工作空间弧面的大小。

根据此操作臂的结构可分析其运动性能,分析上述实验结果可得,当θi=-30°～30°、θi=-60°～60°其工作空间W的关系为>W-60°～60°>W-30°～30°,即θi的变化范围越大,操作臂的工作空间越大,θi与操作臂工作空间正相关。

3.1.2 Δ对工作空间的影响

其中空间点云图表示操作臂在空间中任意的位置点,将空间位置点图对应的空间位置坐标图在坐标系中,由于在本组实验中取θi=-30°～30°,所以操作臂的工作空间弧面大小一定。

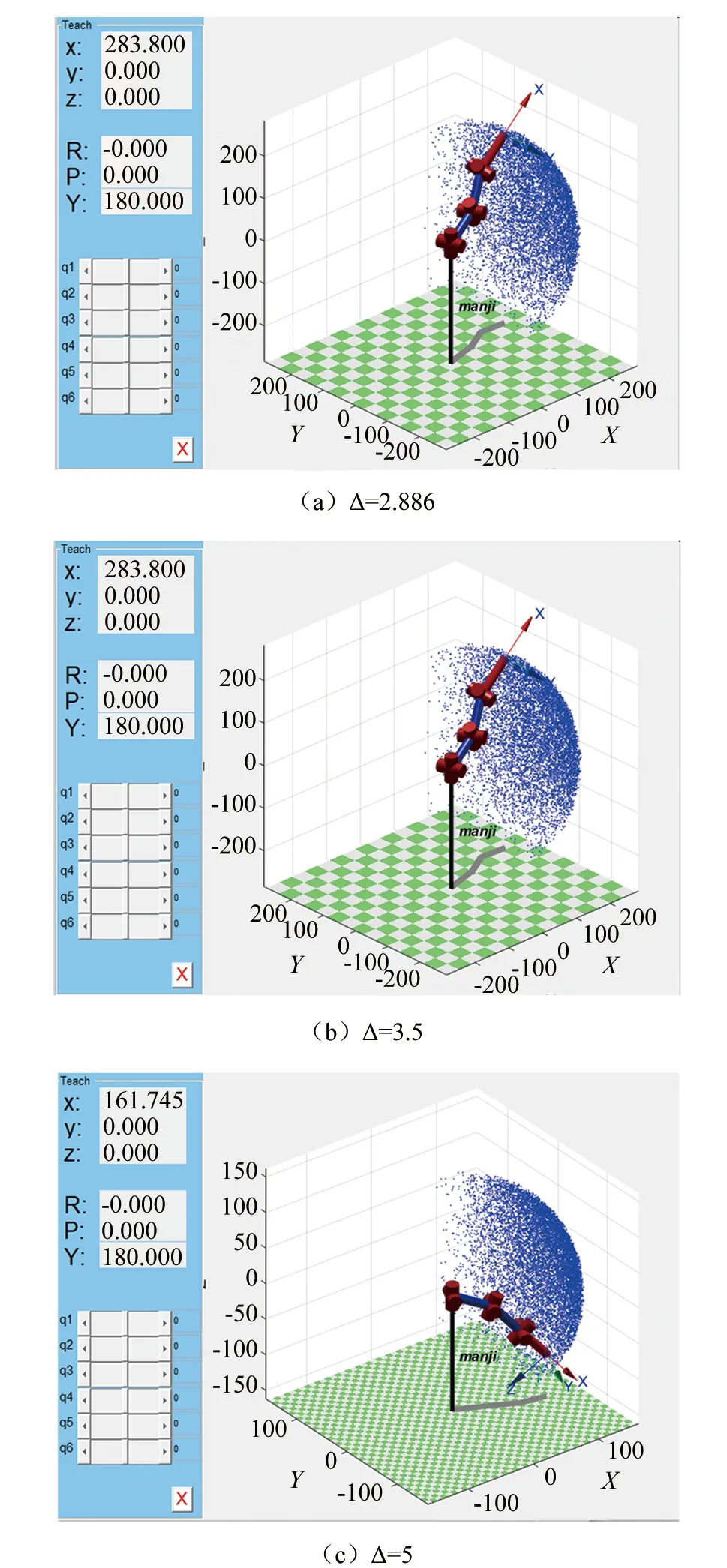
▲图7 工作空间中位置状态结果

根据此操作臂的结构可分析其运动性能,分析上述实验结果可得,当Δ=2.886、Δ=3.5、Δ=5时,其工作空间W的关系为W0>W2>W5,分析上述实验结果可得,当Δ取值越大,即L的范围越小时,操作臂的可工作空间越小,即Δ与操作臂工作空间负相关。

3.2 动力学仿真

建立实验简化模型。根据动力学模型分析,该操作臂所需驱动力由其到达末端位置的加速度定。θi=-30°～30°,L=2(dcosγ+lsinβ)+h1其中Δ=2.886mm～5 mm,为一取值范围内随机变量,Δ决定操作臂的长度。当操作臂在同一末端位置时,可对应多组不同的θi与Δ取值。实验通过给定操作臂末端位置,给定不同的Δ取值,来计算出操作臂相应的位置、速度、加速度。做Δ=2.886、Δ=5两组对比实验,其实验结果如图8所示。

▲图8 速度、加速度和位置关系图

根据动力学仿真计算出操作臂从起始点到末端点的位置状态与速度、加速度的变化。两组实验条件设置为初始位置和末端位置相同,初始位置为(83,0,0),末端位置为(85,93,0)初始关节角设置为[0 0 0 0 0 0]。

从实验结果可知,当在同一位置,且操作臂的关节角度变化范围相同。由图8(a)的速度、加速度图可知,当Δ=0时操作臂的最大速度差为5.67,最大加速度为18.56;由图8(b)的速度、加速度图可知,当Δ=5时操作臂的最大速度差为0.75,最大加速度为2.13;即Δ越小,操作臂末端的最大速度越大,操作臂稳定性越差,Δ与操作臂末端的稳定性为正相关。

4 结论

本文提出了一种刚柔耦合变径操作臂。该操作臂的特点是由一系列的刚性伸缩骨架组成,这种结构使得操作臂具有可伸缩改变自身直径的功能,同时能在保证自身刚度的情况下扩大其工作空间。本文分析了该操作臂可直径的范围并对可伸缩工作空间进行了分析,建立了该操作器的运动学模型和动力学模型,从操作臂的直径变化和单位骨架偏移角度变化研究其对于操作臂工作空间的影响,以及对操作臂稳定性的影响。

通过参数和工作空间试验,验证了刚柔耦合变径操作臂具有良好的运动性能。本研究将线控和杆控相结合,以线控作为主要的控制策略,杆控作为被动控制用于提高整个操作臂的精度。刚柔耦合变径操作臂基于其变刚度、变直径,线控、杆控相结合的特征,在变刚度作业,变直径作业以及高精度作业等方面具有很好的应用前景。另一方面,在实验中也发现刚柔耦合变径操作臂随着直径的变小其工作空间变大,其末端位置的误差趋势变大。在接下来的研究中将着重于研究该操作臂随着工作直径变小时的末端位置误差的补偿[20-21]。

未来,刚柔耦合操作臂拟应用于四足机器人作为载体的变电站巡检机器人上。