“玩转数学”与常规教学的融合实践

苏国东

摘 要：基于《义务教育数学课程标准（2022年版）》相关理念，笔者尝试将“玩转数学”綜合与实践活动和常规教学融合，设计出一节“填幻方”数学活动课.学生通过组队研究、合作展示、开拓创新，在真实情境中发现和提出问题，分析和解决问题，获得基本的数学活动经验，感悟数学的魅力与价值，逐步形成核心素养.

关键词：玩转数学；常规教学；数学活动；填幻方

“玩转数学”是我市面向初中生开展的一项综合与实践活动，活动主要包括学生组队研究、撰写报告、展示答辩三个环节.基于初中教材中的实验与探究、数学活动等栏目内容，融入“玩转数学”的活动形式，开发数学综合与实践活动课程，可以丰富和完善数学常规教学的内容与形式，提升学生的学习兴趣，积累数学活动经验.

1 教学实践

“填幻方”是人教版数学七年级上册第一章“有理数”中实验与探究栏目的选学内容.本节课是在学生学习完用字母表示数的相关知识后设计的一节数学活动课.学生组队开展研究，探讨了幻方中的数字填写方法以及用字母x来表示一般规律的全过程.

1.1 情境引入，问题启发

教师将教材内容扩充，设计出如下问题情境.

幻方是一种将数字安排在正方形格子中，使每行、每列和每条斜对角线上的数字和都相等的方法，也是一种中国传统游戏.三阶幻方（幻方的阶数是指幻方的行或列的数目）是平面幻方中最简单的幻方，已有两千五百多年的历史.相传大禹治水时，洛水中出现了一只“神龟”，其背上有美妙的图案，史称“洛书”，用现在的数字翻译出来，就是三阶幻方.还有人曾建议向火星发射三阶幻方图案，如果火星上有智能生物，那么他们可以从这种“数学语言”中了解到地球上也有智能生物（人类）.

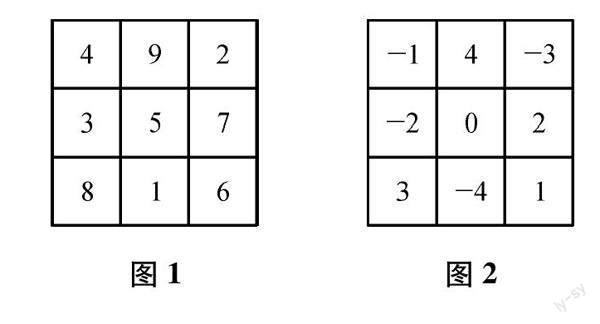
如图1，将1、2、3、4、5、6、7、8、9这9个数字分别填入9个空格中，便得到了三阶幻方的一种填法，每行、每列、每条斜对角线上三个数的和都等于15.

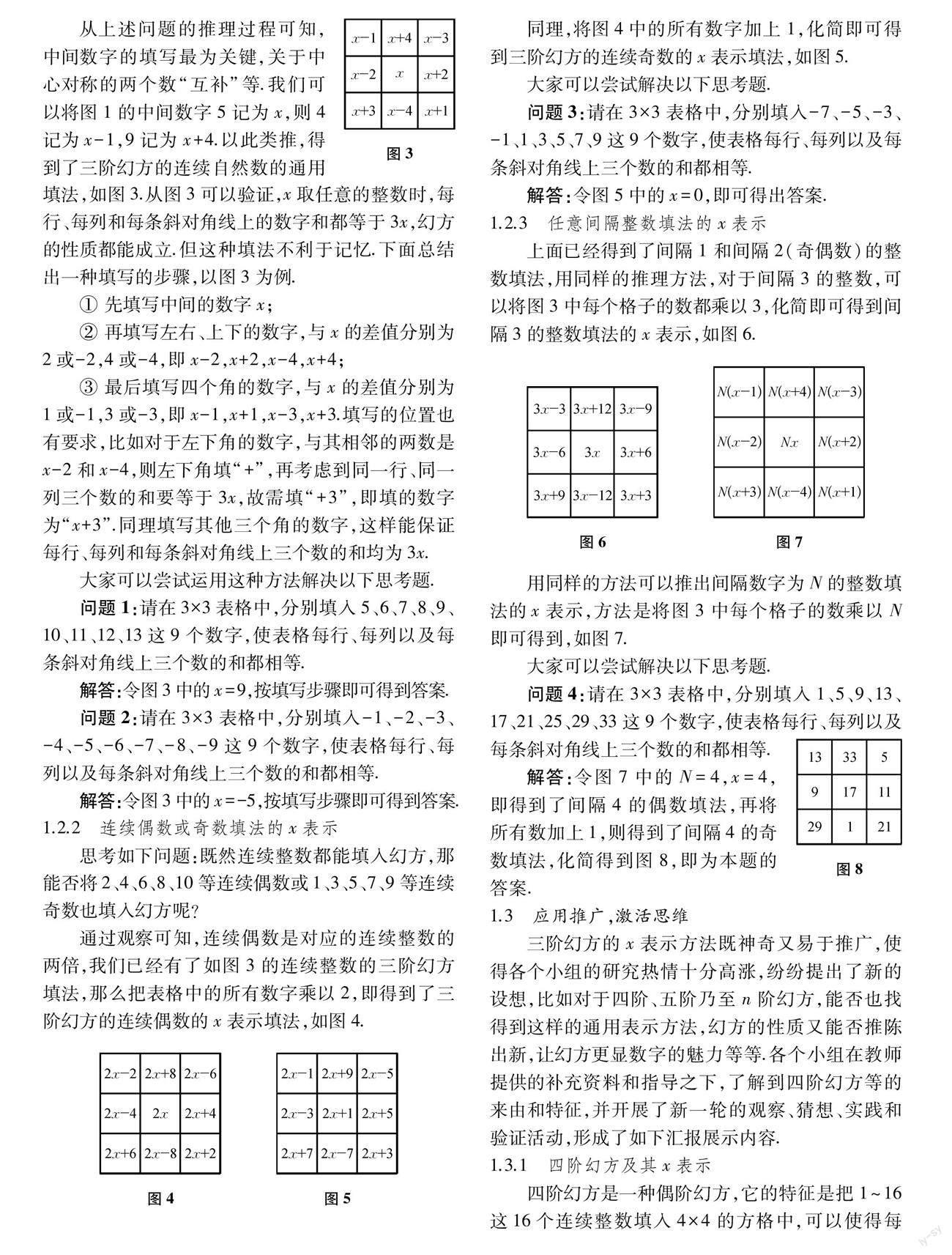
教师在此基础上提出新问题：同学们，你们能将-4、-3、-2、-1、0、1、2、3、4这9个数分别填入三阶幻方的9个空格中，使每行、每列、每条斜对角线上三个数的和都相等吗？你还能在此基础上作出进一步的研究吗？

学生通过不断尝试，探究三阶幻方中的数字规律，得到了不同的填写方法，如图2是其中一种填法.

1.2 组队研究，汇报展示

学生回顾推理过程，通过小组内的交流探讨，得到了快速填写幻方的规律和技巧.然后在教师的引导下，小组成员确定了研究方向，开始探索类似的连续整数的填写方法，并提出对偶数、奇数、任意间隔的整数能否找到填写规律等问题.以下是各个小组的研究思路和汇报展示片段.

1.2.1 连续整数填法的x表示

我们作出如下思考：第一，三阶幻方不容易填，要找到一套步骤才能快速填写；第二，换成其他数字需要重新思考填写方法，较为繁琐，有没有一种通用的填法呢？

通过学习，我们知道了用字母表示数的一般方法，下面探讨是否可以用含字母x的式子来表示各格子的数据，从而解决上述问题.

从上述问题的推理过程可知，中间数字的填写最为关键，关于中心对称的两个数“互补”等.我们可以将图1的中间数字5记为x，则4记为x-1，9记为x+4.以此类推，得到了三阶幻方的连续自然数的通用填法，如图3.从图3可以验证，x取任意的整数时，每行、每列和每条斜对角线上的数字和都等于3x，幻方的性质都能成立.但这种填法不利于记忆.下面总结出一种填写的步骤，以图3为例.

① 先填写中间的数字x；

② 再填写左右、上下的数字，与x的差值分别为2或-2，4或-4，即x-2，x+2，x-4，x+4；

③ 最后填写四个角的数字，与x的差值分别为1或-1，3或-3，即x-1，x+1，x-3，x+3.填写的位置也有要求，比如对于左下角的数字，与其相邻的两数是x-2和x-4，则左下角填“+”，再考虑到同一行、同一列三个数的和要等于3x，故需填“+3”，即填的数字为“x+3”.同理填写其他三个角的数字，这样能保证每行、每列和每条斜对角线上三个数的和均为3x.

大家可以尝试运用这种方法解决以下思考题.

问题1：请在3×3表格中，分别填入5、6、7、8、9、10、11、12、13这9个数字，使表格每行、每列以及每条斜对角线上三个数的和都相等.

解答：令图3中的x=9，按填写步骤即可得到答案.

问题2：请在3×3表格中，分别填入-1、-2、-3、-4、-5、-6、-7、-8、-9这9个数字，使表格每行、每列以及每条斜对角线上三个数的和都相等.

解答：令图3中的x=-5，按填写步骤即可得到答案.

1.2.2 连续偶数或奇数填法的x表示

思考如下问题：既然连续整数都能填入幻方，那能否将2、4、6、8、10等连续偶数或1、3、5、7、9等连续奇数也填入幻方呢？

通过观察可知，连续偶数是对应的连续整数的两倍，我们已经有了如图3的连续整数的三阶幻方填法，那么把表格中的所有数字乘以2，即得到了三阶幻方的连续偶数的x表示填法，如图4.

同理，将图4中的所有数字加上1，化简即可得到三阶幻方的连续奇数的x表示填法，如图5.

大家可以尝试解决以下思考题.

问题3：请在3×3表格中，分别填入-7、-5、-3、-1、1、3、5、7、9这9个数字，使表格每行、每列以及每条斜对角线上三个数的和都相等.

解答：令图5中的x=0，即可得出答案.

1.2.3 任意间隔整数填法的x表示

上面已经得到了间隔1和间隔2（奇偶数）的整数填法，用同样的推理方法，对于间隔3的整数，可以将图3中每个格子的数都乘以3，化简即可得到间隔3的整数填法的x表示，如图6.

用同样的方法可以推出间隔数字为N的整数填法的x表示，方法是将图3中每个格子的数乘以N即可得到，如圖7.

大家可以尝试解决以下思考题.

问题4：请在3×3表格中，分别填入1、5、9、13、17、21、25、29、33这9个数字，使表格每行、每列以及每条斜对角线上三个数的和都相等.

解答：令图7中的N=4，x=4，即得到了间隔4的偶数填法，再将所有数加上1，则得到了间隔4的奇数填法，化简得到图8，即为本题的答案.

1.3 应用推广，激活思维

三阶幻方的x表示方法既神奇又易于推广，使得各个小组的研究热情十分高涨，纷纷提出了新的设想，比如对于四阶、五阶乃至n阶幻方，能否也找得到这样的通用表示方法，幻方的性质又能否推陈出新，让幻方更显数字的魅力等等.各个小组在教师提供的补充资料和指导之下，了解到四阶幻方等的来由和特征，并开展了新一轮的观察、猜想、实践和验证活动，形成了如下汇报展示内容.

1.3.1 四阶幻方及其x表示

四阶幻方是一种偶阶幻方，它的特征是把1～16这16个连续整数填入4×4的方格中，可以使得每行、每列以及两条斜对角线上四个数的和都相等.目前我们要研究的是怎样用含x的式子表达四阶幻方，其次推导出四阶幻方的一些新的性质.

我们先把连续整数1～16填入4×4的方格中组成一个四阶幻方，如图9是其中一种填法.

为了揭示填幻方问题的本质，我们尝试用上面三阶幻方的方法来推出四阶幻方的x表示.把图9中的3记为x，以此类推，可以得出四阶幻方的一种通用的x表示方法，如图10.

1.3.2 推导四阶幻方的新性质

为了方便表示，我们用a1，a2，a3等记号来表示图10中的数字，如图11.利用图10的x表示方法可以方便快捷地得到四阶幻方的一些新的性质.

例如，猜想其具有如下新性质：b2+b3=d1+d4，下面作出证明.

证明：因为b2+b3=x-2+x+12=2x+10，d1+d4=x+10+x=2x+10，

所以，b2+b3=d1+d4成立.

同理，b1+b4=d2+d3，这四个数字所在位置形状类似梯形，故可形象地称之为：

性质（1）：b2+b3=d1+d4；b1+b4=d2+d3（梯形）.

类似的，还可得到如下的一些新性质.

性质（2）：a1+a2+a3+a4=b1+b2+b3+b4=c1+c2+c3+c4=d1+d2+d3+d4.

性质（3）：a1+a3=d2+d4；a2+a4=d1+d3（菱形）.

性质（4）：b1+b2=a4+a3；a1+a2=b4+b3（倒梯形）.

性质（5）：c1+c2=d4+d3；c3+c4=d1+d2（小梯形）.

借助图10的x表示均可验证以上性质.

大家可以综合运用以上知识解决以下思考题.

问题5：请在4×4表格中，分别填入1、3、5、7、9、11、13、15、17、19、21、23、25、27、29、31这16个数字，使表格每行、每列以及两条斜对角线上的数字之和都相等.

解答：把图10中的每个数乘以2，再加上1，即可得到四阶幻方的连续奇数填法，如图12.再令x=2，即得到问题的解答，如图13.

问题6：如图14，四阶幻方中已知部分数据，求a4，d1，d2，d3代表的数字.

解答：由（3）菱形性质：a1+a3=d2+d4，得14+8=d2+6，所以，d2=16.再由（5）小梯形性质：a2+a3=d2+d3，得28+8=16+d3，所以，d3=20.同理，由a1+a2=d1+d2，得14+28=d1+16，所以，d1=26；由a1+a4=d1+d4，得14+a4=26+6，所以，a4=18.

1.4 总结反思，开拓创新

根据上面的推导及所学知识，小组成员还尝试用上述方法展示出了五阶幻方的x表示，学生认为六阶、七阶乃至n阶幻方都可以用类似的方法表达，并据此可以进一步探究对应的连续奇偶数表示、间隔N的数字表示、小数填法等，以及推出n阶幻方的一些新的性质.

在课堂小结阶段，各个小组成员均表示，由于现有的知识还不够丰富，该问题并未得到解决.相信在将来经过不断地学习和经验的积累，他们能够用更多新知识和新工具去研究和解决这些问题，还可以创造各种新的变形幻方的填法，例如，3×4型、4×5型、错位补角型（台阶型）等等，他们对数学问题的学习和思考会不断向纵深方向发展.

2 结束语

在《义务教育数学课程标准（2022年版）》的理念引领下，本节课尝试将“玩转数学”活动融合到初中数学常规教学中，注重创设启发式的教学情境，激发学生学习的兴趣，鼓励学生积极思考、组队研究、合作展示、开拓创新.学生在真实情境中发现问题和提出问题，继而组队探索幻方填法的字母表示，通过观察、猜测、试验、计算、推理、验证等方式分析问题和解决问题，获得良好的数学活动经验，感悟数学的魅力和应用价值，逐步形成核心素养.

参考文献：

［1］ 伍晓焰.构建初中数学活动 促进师生共同发展——广州市初中“玩转数学”创新活动的开发与实践［J］.中国数学教育，2021（Z3）：49-58+68.

［2］ 顾广林.初中数学活动课教学策略［J］.教学与管理，2014（22）：64-66.

［3］ 于道洋，宁连华.试论墨家的理性精神及其对数学教育的启示［J］.数学教育学报，2021（5）：87-91.