“学科大概念”视域下单元复习课教学设计研究
2023-07-20陈海岚
陈海岚
摘 要:数学学科大概念提出“单元—课时教学”的教学模式,引导教师建构学科知识网络,促使课时与学科知识系统化、深入化,达成发展学生核心素养、立德树人的教育目标.单元复习是课时教学的最后一个环节,在教学中有巩固单元知识,深化单元思想的作用.本文以“函数的概念和性质”复习课为例,从单元知识、单元目标、单元思想、典例讲评四个环节反思如何设计一节符合学科大概念理念的单元复习课.
关键词:大概念函数单元复习;教学设计;核心素养
《普通高中数学课程标准(2017年版)》指出:“进一步精选学科内容,重视以学科大概念为核心,使课程内容结构化,以主题为引领,使课程内容情境化,促进学科核心素养的落实”.学科大概念为落实学科核心素养提供了重要的指引,为一线教学提供了有效的抓手.数学学科大概念能够促进学生对数学本质的理解;培养学生运用数学进行探究并解决问题的能力.
1 “学科大概念”的理解
大概念(Big Ideas),仅仅从字面上来看,可以理解为大观念、大思想、大想法.数学学科大概念不是指具体的数学知识,如数学概念、数学公式等,而是指反映数学学科本质、学科思想和解决问题的一般观念,具有抽象性、概括性、统摄性的特征,如:函数与数学模型,解析几何和坐标化等.
2 基于大概念的教学设计
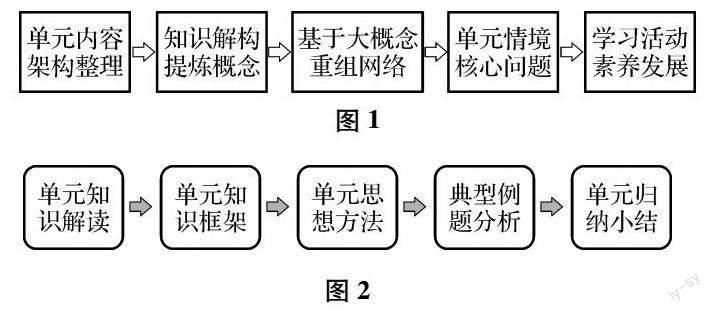
基于学科大概念的单元复习设计思路(如图1),以整理单元知识为主线,重视思想的领悟、方法的提炼,并设计符合单元情境的核心问题,供学生进行学习和探究,通过问题的解决让数学学科大概念落地生根,真正实现培养学生的数学核心素养.
3 “函数的概念和性质”单元复习课教学设计
“函数的概念和性质”的单元复习课的设计思路是:单元知识解读—单元知识框架—单元思想方法—典型例题分析—单元归纳小结(见图2).
3.1 单元知识解读
单元知识解读旨在解读单元知识的内容、思想、素养、地位与目标解读,给学生以“会当凌绝顶,一览众山小”之感.
3.1.1 单元架构和知识重组
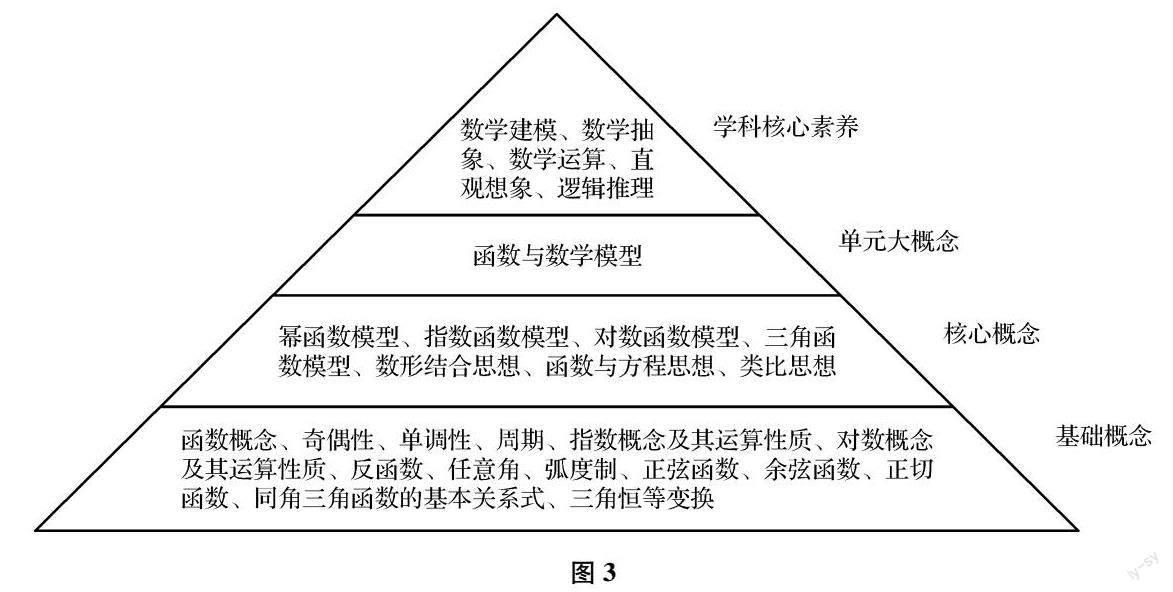
函数单元的大概念是“函数与数学模型”,基于此,设计出本单元的概念金字塔(见图3).
函数单元的教学的终极目标是发展学生的关键能力,落实学生的学科核心素养,因此金字塔的塔尖是學科核心素养;第二层是函数单元的大概念——“函数与数学模型”,单元大概念的获得可以通过对教材和课程标准的分析;第三层是函数单元的核心概念和重要数学思想方法;塔底是函数单元的基础概念和重要知识.
3.1.2 单元目标的确定
(1) 理解函数的概念,能够从变量之间的依赖关系、实数集合之间的对应关系、函数图象的几何直观等多个角度整体认识函数概念,体会集合语言与对应关系在描述函数概念中的作用;了解函数的三要素、函数的三种表示方法以及区间的概念.
(2) 掌握函数的性质,经历从“数学直观—文字语言—定性描述—定量刻画”的过程,认识到函数图象是研究函数性质的重要载体,从特殊到一般,抽象出用数学语言精准地描述函数的性质,发展学生的
数学抽象、数学推理核心素养.
(3) 按照“事实—概念、图象—图象特征—性质—应用”的基本流程研究幂函数,从数学背景或实际背景(事实)引出函数的形式(概念),列表描点作图(图象),然后观察图象特征,接着猜想结论并论证(性质),最后对性质加以应用.让学生体会从“形”和“数”两个角度研究函数的思想方法:“形”指的是图形直观,通过图形直观地发现函数的变化规律;“数”指的是代数运算,通过代数运算严格论证函数的解析式和函数的性质,从而发展学生的直观想象、数学抽象、逻辑推理素养.
(4) 函数应用,用具体的函数模型解决简单的实际问题和数学问题.通过对问题的分析、研究和解决,领悟函数是刻画客观事物变化规律的模型,从而构建“函数与数学模型”的大概念.
3.2 单元知识框架
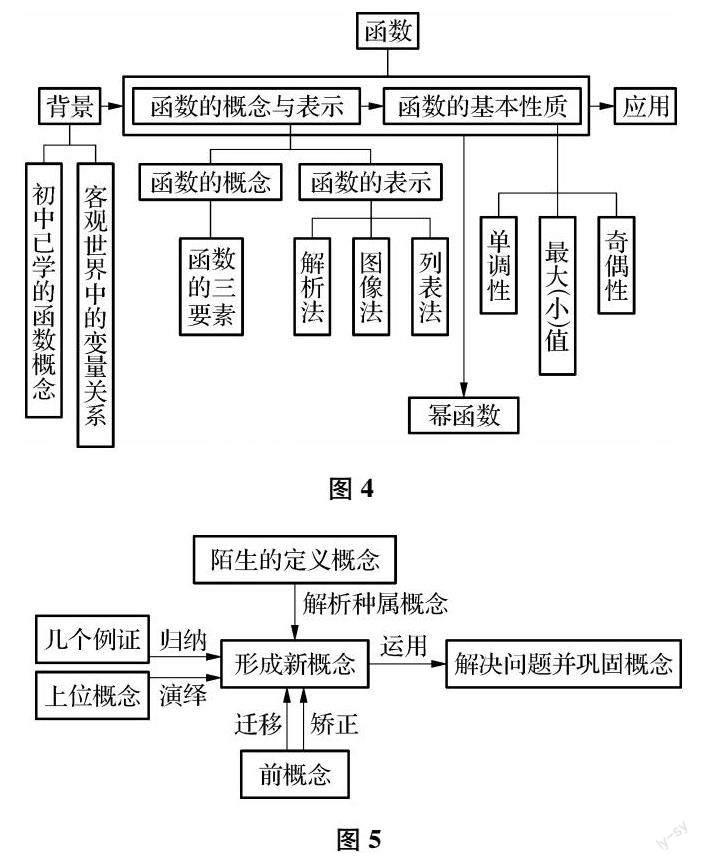
单元知识框架,简而言之就是本章内容的思维导图.知识框架的作用就是梳理单元知识内容、发展脉络,使单元知识间的关系更清晰,单元知识间的逻辑关系更明朗,帮助学生建立单元知识的认知结构图,促进学生基本知识基本技能的获得.“函数的概念和性质”这个课时单元的内容框图如图4所示.
3.3 单元思想方法
单元思想方法的复习,突出了数学知识的研究路径,有助于提升学生解决问题的能力,同时也是落实核心素养的关键环节.函数单元主要有两个研究路径:一是数学概念的发生发展过程(如图5);二是函数性质的研究思路,重要的思想是建立函数模型解决实际问题.
3.3.1 数学概念的发生发展路径
本章中第一个要建构的是以“集合—对应”说来表达的函数概念,遵循了数学概念生成的基本路径,按照“具体函数”—“类函数”—“变量说”—“集合对应说”的路线展开.在这个过程中渗透了特殊到一般思想,发展了学生的数学抽象、逻辑推理的核心素养,培养了学生用数学的眼光看待现实世界,用数学的语言表达现实世界.
3.3.2 函数性质的研究思路
本章呈现出函数性质的研究基本路径是:事实—概念、图象—图象特征—性质—应用.
函数具有“数”与“形”的双重特征,在借助函数图象探索函数的性质时便体现了学生的直观想象素养;通过数学运算,来归纳函数的概念,体现了数学中用“运算”表达规律的思想,培养了学生数学运算、逻辑推理的核心素养.
3.3.3 函数与“函数模型”
函数是刻画客观事物运动变化的模型,以具体函数为载体,“表达”客观现象的变化规律,通过研究函数的性质来研究客观事物的变化,认识函数在解决实际问题中的作用.
在构建函数模型的过程中,培养了学生的两个思想:一是通过函数模型,精确地表达客观事物中一个量是如何随着另一个量的变化而变化;二是通过代数运算、图象直观,研究函数的性质从而了解客观事物的变化规律,在这个过程中,培养了学生运用函数的思想和方法描述和解决实际问题的能力,有效提升了学生的运算素养、直观想象与数学建模核心素养.
3.4 典例讲评
典例讲评是单元复习课的重要一环,是教师在复习单元知识和思想方法之后,根据单元核心内容,所设计的适用于学生实战环节,能够有效地反馈出学生对单元知识和思想方法的理解和掌握程度,同时为学生解决单元核心问题积累活动经验,并再一次提炼了单元大概念.
在“函数的概念和性质”这一单元中,函数性质的研究过程体现了本单元主要思想和方法,因此与之相关的习题成为课堂选题的出发点.
教学设计中具体如下:引入:给出函数y=x+1x.
问题1:根据本章知识和思想,你能设计出这个函数的研究路径吗?
追问1:你要用什么方法研究这个函数?
追问2:你认为可以从哪些方面研究这个函数?
追问3:你想如何画出该函数的图象?
追问4:你想研究该函数的哪些性质?
追问5:你想如何研究该函数的值域?研究的依据是什么?
追问6:如何研究该函数的奇偶性和单调性?
追问7:奇偶性在研究函数性质的过程中能起到怎樣的作用?
追问8:通过刚才的研究,你能得出该函数的值域吗?
【设计意图】通过设计开放性的问题和一个问题串,引导学生层层递进地回顾本章的知识内容,复习研究函数的一般过程,思考函数的研究路径,提炼函数研究的一般方法,最后突出研究对象的一般化.值得一提的是,在这个过程中,引导学生思考函数性质研究的先后顺序安排,体现了“整体—局部—整体”的研究路径.
问题2:你能通过运算的角度研究这个函数吗?在这个角度下,你的研究对象和研究路径该如何确定呢?
【设计意图】通过“数学运算”研究函数,让学生感受基本初等函数复合形成新函数的过程,在这个过程中认识复合函数与基本初等函数之间整体与部分的关系,培养学生从多个角度思考问题的创新精神,更进一步落实学生“提出问题”的能力.
4 反思小结
学科大概念视域下的单元复习课,以获得数学概念为目标和指引,复习单元主干知识,构建知识网络,关注思想方法、一般概念的渗透,通过设计典型的、开放性、创新性的问题,激发学生对知识思考和思想方法的领悟,提升学生解决问题的能力,落实学生核心素养的发展.
参考文献:
[1] 章建跃.核心素养立意的高中数学课程教材教法研究:上卷[M].上海:华东师范大学出版社,2021.
[2] 黄炳锋.素养涵育:高中数学“片段教学”的理解与实践范式构建[J].福建基础教育研究,2020(7):4952.
[3] 冯维清.“题族”教学设计的探索:以《数列》的章末复习课为例[J].中学数学教学,2021(4):3335.
[4] 黄翔,童莉,李明振,等.从“四基”“四能”到“三会”[J].数学教育学报,2019(5):3740.
