兼顾经济与控制性能的过程分程控制系统结构设计
2023-07-19许锋沈慧刚刘尧东罗雄麟
许锋 沈慧刚 刘尧东 罗雄麟

摘 要 随着流程工业对于降低成本和提高收益等经济性能要求的不断提高,希望控制系统在操纵变量对被控变量实施控制的同时尽可能减小对操作费用的影响。对于非方胖系统,由于操纵变量维数多于被控变量维数,当被控变量偏差较小时期望采用对经济性能影响小的操纵变量进行控制,只有当被控变量偏差较大、无法满足控制要求时,才期望将对经济性能影响大、响应速度快的操纵变量投入控制。对此,传统的单回路控制结构不能满足过程控制问题的经济要求。因此,基于非方系统的相对能量增益阵列,对胖系统进行变量配对分析,提出一种胖系统分程控制系统结构设计方法。该方法兼顾经济与控制性能,实现一个被控变量和分别侧重经济性能与控制性能的两个操纵变量的配对。通过实例分析说明,胖系统的分程控制系统结构设计方法不仅能够得到合理的变量配对,满足控制性能要求,而且能够保持经济性能尽可能优化。
关键词 过程控制 经济优化 多变量系统 控制回路配对 分程控制
中图分类号 TP273 文献标识码 A 文章编号 1000?3932(2023)03?0291?08
基金项目:国家自然科学基金项目(21676295)。
作者简介:许锋(1976-),副教授,从事过程控制与系统工程方面的研究,xufeng@cup.edu.cn。
引用本文:许锋,沈慧刚,刘尧东,等.兼顾经济与控制性能的过程分程控制系统结构设计[J].化工自动化及仪表,2023,50(3):291-298.
随着工业过程生产规模的不断扩大,企业对于降低成本和提高收益等经济性能方面的要求越来越高。在工业过程中,为了实现经济效益最大化,在优化控制的同时需要寻求过程操作条件的最优,以减少能耗、保证产品质量和增加产品收益[1,2]。
然而在实际生产过程中,系统经济优化变量和控制优化变量可能存在寻优变化方向的不一致,从而造成在线优化结果不可实现的问题。因此为了满足在线优化结果在实际过程中的可实现性,文献[3]提出基于动态模型的变约束迭代优化方法,文献[4]把神经网络与在线优化进行了有机结合,文献[5~8]将实时优化与底层控制结合起来,文献[9~12]采用了反馈实时优化方法。文献[13]在优化控制层的目标函数中加入对操纵变量的控制限制,对于实时优化与优化控制分层周期不同的问题,提出两层优化控制策略,使得过程经济目标更好。所以,控制与优化的结合已经成为多变量系统控制结构设计的重要考虑方向。从上述文献可以看出,要实现过程经济效益最大化,需要协调和权衡过程经济目标和控制目标。
对于多变量系统,由于变量之间相互关联的影响,降低了闭环系统的控制性能[14],因此进行控制回路设计时首先要对系统进行关联分析以及变量配对,使得各回路间的相互作用降到最低。在多变量系统的关联分析和变量配对方法中,目前应用最广泛的就是BRISTOL E H提出的相对增益阵[15](Relative Gain Array,RGA)和由此发展的相关方法。由于RGA只是利用系统的稳态信息而忽略了系统的动态特性,因此在其基础上提出了各种基于动态信息的改进方法。叶凌箭等[16]、GAGNEPAIN J P等[17]和罗雄麟等[18]分别基于被控系统的开环单位阶跃响应进行时域分析,提出平均相对增益矩阵(Average Relative Gain Matrix,ARGM)、平均相对关联阵列(Average Relative Interaction Array,ARIA)和动态RGA,以此来衡量多变量系统变量之间的关联程度。MEEUSE F M等[19]、Mc AVOY F M等[20]分别提出了基于最优性能控制器定义和计算动态RGA的方法。XIONG Q等[21~24]提出了有效相对增益矩阵(Effective Relative Gain Array,ERGA),考虑了稳态增益和带宽这两个开环系统重要的动态特征,其计算相对简单且与控制器无关。HE M J等提出了归一化相对增益矩阵(Relative Normalized Gain Array,RNGA),利用过程的稳态增益确定稳态信息,而动态信息则采用误差积分指标进行评价,最终推出RNGA[25]。任丽红等[26]在RNGA的基础之上,根据误差平方积分准则定义了能量消耗矩阵,结合稳态增益定义了相对能量增益矩阵(Relative Energy Gain Array,REGA)。REGA通过结合过程的稳态信息和动态特性,对RNGA进行了改进,弥补了RNGA的不足并能快速而准确地得到配对方案。
随着流程工业的不断发展,生产过程越来越多地出现非方系统。CHANG J W和YU C C将RGA推广到非方系统中得到非方相对增益矩阵(Non?square Relative Gain Array,NRGA)[27],SKOGEST?AD S和POSTLETHWAITE I总结了NRGA的性质[28],任丽红等基于REGA提出了非方相对能量增益矩阵(Non?square Relative Energy Gain Array,NREGA)[29]方法。
目前,多变量系统通过RGA设计的控制回路一般采用单回路控制,在简单控制回路控制已经无法满足工业过程控制要求的前提下,必须利用RGA对系统进行复杂控制的分散常规控制设计。袁未未等通过对大系统进行输入/输出变量划分,根据工艺过程将被控变量划分为主要被控变量和次要被控变量,输入变量分为可调输入变量和非可调输入变量[30~32]。一般可调输入变量的个数多于主要被控變量,而不可调输入变量的个数少于被控变量,因此子系统中有瘦系统,也有胖系统。在复杂控制系统中,一个串级控制回路中包含一个副被控变量和一个主被控变量,因此可以解决一个输入变量和多个输出变量配对的问题;而前馈-反馈控制回路可以解决一个输出变量和多个输入变量配对的问题。
随着流程工业对于经济性能要求的不断提高,希望控制系统在操纵变量对被控变量实施控制的同时尽可能减小对操作费用的影响。因此,笔者基于非方相对能量增益矩阵,针对输入变量多于输出变量的非方胖系统,提出一种分程控制系统结构设计方法,这种方法可以实现两个操纵变量和一个被控变量的相互对应。当被控变量偏差较小时,将对经济性能影响小、响应速度慢的操纵变量投入控制;当被控变量偏差较大时,对经济性能影响小、响应速度慢的操纵变量已经达到极限,再无法满足控制要求,这时将对经济性能影响大、响应速度快的操纵变量投入控制,这种方案既可以实现对系统的控制,又能够保持经济性能尽可能优化,做到控制性能与经济性能的兼顾。最后利用实例进行了仿真分析和研究,说明本方案针对胖系统可以得到合理的分程控制的变量配对,并且协调系统的经济目标和控制目标。
1 NREGA
1.1 定义
假设非方多变量系统的传递函数矩阵为:
1.2 性质
NREGA基于REGA并针对非方系统,具有和REGA相似的性质,在利用NREGA进行分散控制系统设计时,在选择配对方案时应遵循以下规则:
a. 所有选择配对的NREGA元素必须是正数;
b. 被选择配对的NREGA元素必须接近于1;
c. 太大的NREGA元素应避免选择配对。
同时由于NREGA针对非方系统,计算得到的能量增益矩阵K是非方阵,所以存在以下两种情况:
a. 当K为行满秩时,则NREGA的每行元素和为1,每列元素和小于1;
b. 当K为列满秩时,则NREGA的每列元素和为1,每行元素和小于1。
2 兼顾经济与控制性能的分程控制系统结构设计
2.1 分程控制系统
分程控制系统广泛应用于石油、化工工业的过程控制中,主要用来满足特殊的工艺要求。分程控制的功能主要有两个:一是从改善调节系统品质的角度出发,用分程调节扩大调节阀的可调范围;二是用于控制两种不同的介质,以满足工艺生产要求。
在分程控制系统中,一个控制器的输出同时送往两个或多个执行器,而每个执行器的工作范围不同。其控制系统框图如图1所示,可以看出,分程控制系统有两个操纵变量和一个被控变量,属于典型的胖系统。通过分程控制,可以实现两个操纵变量和一个被控变量的相互对应,充分利用系统所有的输入信息,从而满足系统的控制要求。
2.2 胖系统的分程控制系统结构设计
对于输入变量多于输出变量的胖系统,如果仅仅设计单回路的简单控制系统,往往很难对所有输入变量进行有效利用,无法满足控制要求;同时,当多个操纵变量对同一被控变量产生影响时,对经济性能影响较小的操纵变量希望得到更多的应用,只有当被控变量偏差较大、无法满足控制要求时,才将对经济性能影响大、响应速度快的操纵变量投入控制。基于以上两点,传统的单回路控制既无法满足控制要求,也无法满足经济要求。而分程控制系统由于存在两个操纵变量和一个被控变量,这样通过这两个操纵变量协调系统的控制要求和经济要求,因此可以实现控制性能和经济性能的兼顾。
针对胖系统,根据NREGA的性质,笔者提出一种兼顾经济与控制性能的常规分散控制系统结构设计方法。
基于胖系统输入对输出的传递函数矩阵,由于其NREGA的列元素和小于1,所以将NREGA的列元素和从大到小排序,从中可以看出,列元素和越接近于1,说明这列向量所对应的输入对系统的动态调节响应速度越快。
对于系统经济性能指标,基于输入对经济性能指标的传递函数行向量,也可以求出对应的NREGA行向量,其列元素均小于1,将所有的列元素从大到小排序,列元素越接近于1,说明此列所对应的输入对系统的经济性能影响越大。
这样,通过比较系统的输入变量对输出变量的动态调节响应速度快慢和对经济性能指标的影响大小,找出具有对应相同被控变量的两个操纵变量进行分程控制结构设计。对经济性能影响大、响应速度快的操纵变量作为分程控制器输出高信号区间的控制变量;而对经济性能影响小、响应速度慢的操纵变量则作为分程控制器输出低信号区间的控制变量。
通过该设计方法,当被控变量偏差较小时,将对经济性能影响小、响应速度慢的操纵变量投入控制;当被控变量偏差较大时,对经济性能影响小、响应速度慢的操纵变量已经达到极限,无法再满足控制要求,这时将对经济性能影响大、响应速度快的操纵变量投入控制。这样,既可以满足对系统的控制要求,又能够实现经济性能尽量优化,做到控制性能与经济性能的兼顾。
然后选择Λ′中列元素和大的m个操纵变量,这m个变量即为兼顾动态响应速度和经济效益的操纵变量,对应分程控制的低信号区间,用于被控变量偏差较小的控制。将这m个操纵变量与所有被控变量组成系统G:
然后对G进行方系统的REGA计算,选择与被控变量相匹配的操纵变量。同时Λ′中列元素和最小的n-m个操纵变量所代表的就是对经济效益影响较大的操纵变量,但是也有可能出现对系统动态响应速度快、控制性能较好的操纵变量,所以将这n-m个操纵变量与所有被控变量组成一个m×(n-m)维的瘦系统G:
然后对G进行非方瘦系统的NREGA计算,选择与被控变量相匹配的操纵变量。这样所得到的操纵变量就是响应速度快,但是经济效益差的操纵变量,对应分程控制的高信号区间,用于被控变量偏差较大时的控制,实現对系统的快速控制。
这样当G和G配对完成后,对具有相同被控变量的两个操纵变量进行分程控制结构设计。第1步选择的操纵变量作为分程控制器输出低信号区间的控制变量;而第2步所得到的操纵变量作为分程控制器输出高信号区间的控制变量。
3 实例分析
本节将对输入变量维数多于输出变量维数的胖系统使用第2节中的方法进行常规控制系统的结构设计。
3.1 例1——Shell系统
以Shell公司的典型控制问题[33]为例,其三入两出系统的传递函数矩阵为:
系统传递函数矩阵的NREGA的列元素和为0.352 7、0.988 0、0.659 3,NREGA各行分别减去系统经济性能指标的NRGA值,然后进行比较,可以发现u是一个对经济性能影响大、响应也快的操纵变量。因此,将u、u与被控变量组成方系统,将u与被控变量组成瘦系统,分别求取REGA進行变量配对,配对结果为:{y~u,y~u},{y~u},因此,y~u组成单回路控制系统,而y~u~u组成分程控制系统,其中,u作为分程控制的低信号区间的控制变量,用于被控变量偏差较小时的控制,u作为分程控制的高信号区间的控制变量,当被控变量出现较大偏差时,可以实现对系统的快速控制。
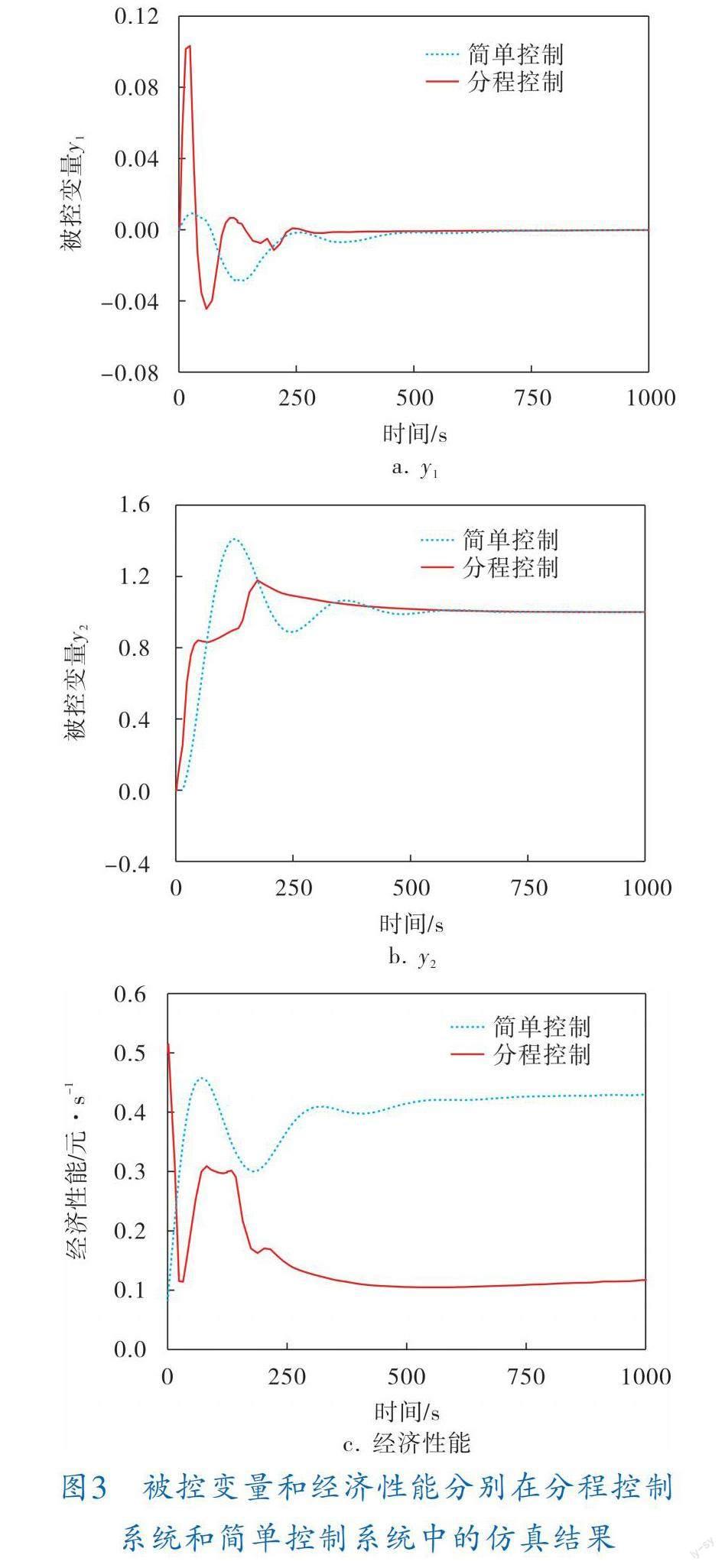
图2和表1是例1的仿真结果。由图2可以看出,多变量分程控制系统达到稳定的时间比简单控制系统达到稳定的时间要长,达到稳定之前具有较大的超调量,但是经过一段时间后依然可以达到稳定,且其在经济性能(操作费用)方面的表现要优于简单控制系统,分程控制系统的经济性能曲线在简单控制之下。由表1可以看出,分程控制结构设计方法相比较于简单控制,平方偏差积分控制性能指标较大,说明分程控制系统对于系统的控制性能有一定的影响,但是平均经济指标较小。所以通过本文方法在满足系统控制的同时,能够保证经济性能的尽可能优化,降低操作成本。
系统和简单控制系统中的仿真结果
3.2 例2——3×2的精馏过程
3×2精馏过程[34]三入两出系统的传递函数矩阵为:
系统传递函数矩阵的NREGA的列元素和为0.125 5、0.880 0、0.994 5,NREGA各行分别减去系统经济性能指标的NRGA值,然后进行比较,发现u是一个对经济性能影响大、响应也快的操纵变量。因此,将u、u与被控变量组成方系统,将u与被控变量组成瘦系统,分别求取REGA进行变量配对,配对结果为:{y~u,y~u},{y~u},因此,y~u组成单回路控制系统,y~u~u组成分程控制系统,其中,u作为分程控制的低信号区间的控制变量,用于被控变量偏差较小时的控制,u作为分程控制的高信号区间的控制变量,当被控变量出现较大偏差时,可以实现对系统的快速控制。
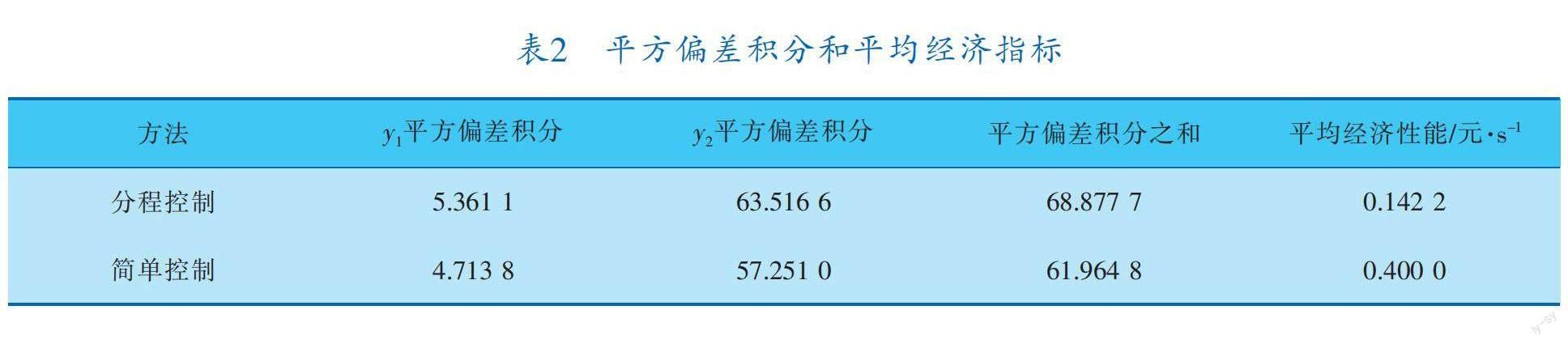
图3和表2是例2的仿真结果。由图3和表2可以看出,相较于简单控制,多变量分程控制系统达到稳定的时间较长,在达到稳定之前具有较大的波动,但这些波动都在可控制范围之内,系统平方偏差积分控制性能指标与简单控制相差不大,但是在经济性能方面,分程控制系统则具有明显的优势。
4 结束语
随着过程控制领域对于降低生产成本和提高经济收益等要求的日益重视,抛开已形成商业产品的多变量系统集中控制手段之外,对于常规控制而言,多变量系统的经济优化发展较为缓慢,如何在解决操纵变量对被控变量进行控制的同时减少操作成本成为考虑的重点。笔者针对系统本身,对输入变量多于输出变量的胖系统的控制结构设计提出了分程控制的方法。仿真结果表明:该方法不仅能够得到合理的变量配对,实现对系统的控制,而且能够使得经济性能尽可能优化,从而减少过程操作成本,做到控制性能和经济性能的兼顾,具有很强的实际意义。
参 考 文 献
[1] 万百五.大工业过程计算机在线稳态优化控制[M].北京:科学出版社,1998.
[2] 白金麟,石立宏,周培湘,等.化工过程实时优化技术现状与未来[J].数字石油和化工,2009(7):2-6.
[3] 杨斌,张其方,许锋,等.基于动态响应的变约束迭代优化及其在化工过程操作优化中的应用[J].计算机与应用化学,2011,28(12):1521-1526.
[4] SAFAVI A A, NOORAII A, ROMAGNOLI J A. A hybrid model formulation for a distillation column and the on?line optimisation study[J].Journal of Process Control,1999,9(2):125-134.
[5] ZANIN A C,GOUV?A M T D,ODLOAK D.Integrating real?time optimization into the model predictive contro?ller of the FCC system[J].Control Engineering Practi?ce,2002,10(8):819-831.
[6] ATSUSHI M,MARLIN T E,HRYMAK A N.Operations optimization and control design for a petroleum distill?ation process[J].Canadian Journal of Chemical Engin?eering,2010,73(6):896-907.
[7] CUTLER C R,PERRY R T.Real time optimization with multivariable control is required to maximize profits[J].Computers & Chemical Engineering,1983,7(5):663-667.
[8] GARCIA C E,MORARI M.Optimal operation of integr?ated processing systems:Part Ⅱ:Closed?loop on?line optimizing control[J].AIChE Journal,1984,30(2):226-234.
[9] VISSER E,SRINIVASAN B,PALANKI S,et al.A feed?back?based implementation scheme for batch process optimization[J].Journal of Process Control,1999,10(5):399-410.
[10] ENGELL S.Feedback control for optimal process ope?ration[J].Journal of Process Control,2007,17(3):203-219.
[11] EATON J W,RAWLINGS J B.Feedback control of chemical processes using on?line optimization techniques[J].Computers & Chemical Engineering,1990,14(4):469-479.
[12] MODAK J M,LIM H C.Feedback optimization of fed?batch fermentation[J].Biotechnology & Bioengineer?ing,1987,30(4):528-540.
[13] YING C M,JOSEPH B.Performance and stability ana?lysis of LP?MPC and QP?MPC cascade control syste?ms[J].AIChE Journal,1999,45(7):1521-1534.
[14] SKOGESTAD S,MORARI M.Implication of Large RGA Elements on Control Performance[J].Industrial Engineering Chemistry Research,1987,26(11):2323-2330.
[15] BRISTOL E H.On a new measure of interaction for multivariable process control[J].IEEE Transactions on Automatic Control,1966,11(1):133-134.
[16] 叶凌箭,宋执环.多变量控制系统的一种变量配对方法[J].控制与决策,2009,24(12):1795-1800.
[17] GAGNEPAIN J P,SEBORG D E.Analysis of process interactions with applications to multiloop control system design[J].Ind Eng Chem process Des Dev,1982,21(1):5-11.
[18] 罗雄麟,任丽红,周晓龙,等.常规控制系统配对设计的动态相对增益阵研究[J].化工自动化及仪表,2012,39(3):295-300.
[19] MEEUSE F M,HUESMAN A E M.Analyzing dynamic interaction of control loops in the time domain[J].Industrial & Engineering Chemistry Research,2002,41(18):4585-4590.
[20] Mc AVOY T M,ARKUN Y,CHEN R,et al.A new approach to defining a dynamic relative gain[J].Control Engineering Practice,2003,11(8):907-914.
[21] XIONG Q,CAI W J,HE M J.A practical loop pairing criterion for multivariable processes[J].Journal of Process Control,2005,15(7):741-747.
[22] XIONG Q,CAI W J,HE M J,et al.Decentralized control system design for multivariable processes:A novel method based on effective relative gain array[J].Industrial & Engineering Chemistry Research,2006,45(8):2769-2776.
[23] XIONG Q,CAI W J.Effective transfer function met?hod for decentralized control system design of multi?input multi?output processes[J].Journal of Process Control,2006,16(8):773-784.
[24] XIONG Q,CAI W J,HE M J.Equivalent transfer function method for PI/PID controller design of MIMO processes[J].Journal of Process Control,2007,17(8):665-673.
[25] HE M J,CAI W J,WEI N,et al.RNGA based control system configuration for multivariable processes[J].Journal of Process Control,2009,19(6):1036-1042.
[26] 任丽红,刘雨波,罗雄麟,等.多变量时滞系统的关联分析与变量配对[J].化工自动化及仪表,2012,39(6):743-746.
[27] CHANG J W,YU C C.The relative gain for non?square multivariable systems[J].Chemical Engineer?ing Science,1990,45(5):1309-1323.
[28] SKOGESTAD S,POSTLETHWAITE I.Multivariable Feedback Control:Analysis and Design[M].New York:John Wiley & Sons,1996.
[29] 任丽红,罗雄麟,刘雨波,等.一种新的变量配对方法及其在非方系统中的应用[J].控制与决策,2011,26(2):11-19.
[30] 袁未未,许锋,罗雄麟.过程块分散控制系统结构设计[J].计算机与应用化学,2016,33(10):1096-1102.
[31] 许锋,袁未未,罗雄麟.化工过程非方瘦系统的串级控制系统结构设计[J].化工学报,2017,68(7):2833-2843.
[32] 许锋,袁未未,罗雄麟.大系统的常规控制系统结构设计[J].计算机与应用化学,2017,34(9):661-668.
[33] CHEN D,SEBORG D E.Relative gain array analysis for uncertain process models[J].AIChE Journal,2002, 48(2):302-310.
[34] HUANG H P,OHSHIMA M,HASHIMOTO I.Dyna?mic interaction and multiloop control system design[J].Journal of Process Control,1994,4(1):15-27.
(收稿日期:2022-11-01,修回日期:2022-12-09)
Split?range Control Configuration Design ConsideringEconomic and Control Performance
XU Feng, SHEN Hui?gang, LIU Yao?dong, LUO Xiong?lin
(College of Information Science and Engineering, China University of Petroleum (Beijing))
Abstract The process industrys requirements for cost reducing and profit boosting rise continuously, including the hope for reducing the operating cost as far as possible when controlled variables are adjusted by manipulated variables. Regarding a non?square fat system, the dimension of manipulated variables is more than that of the controlled variables, so the manipulated variables with low influence on economic performance are hoped to be put into control when there are small errors on controlled variables. Only when there are large errors on controlled variables and control requirements cant be meet, the manipulated variables with high influence on economic performance and fast response will be put into control. In this regard, the traditional single?loop control system cant meet economic requirements of the process control. In this paper, the relative energy gain array of non?square system was used to implement interaction analysis, and a split?range control configuration design method was introduced for the fat multivariable system. This method considers both economic performance and control performance, and it realizes the pairing of one controlled variable to two manipulated variables which focusing on economic performance and control performance respectively. Finally, a case study illustrated that, the split?range control configuration design for fat multivariable system can get a reasonable variable pairing and meet the control performance requirement, as well as optimize the economic performance as much as possible.
Key words process control, economic optimization, multivariable system, control loop pairing, split?range control
