小学数学教学中学生解题错误归因及对策研究

摘 要：解题教学是小学数学教学的重要组成部分。目前小学生在解题时仍然存在解题过程混乱、结果不正确等问题。文章基于小学数学解题教学案例，梳理了学生解题错误的原因，同时指出教师可以从基础教学、思维培养教学、解题习惯培养教学三个角度出发开展解题教学工作，以期提高小学数学教学质量。

关键词：小学数学；解题错误；归因；对策

中图分类号：G427                                文献标识码：A                                       文章编号：2097-1737（2023）17-0071-03

引  言

在小学数学解题过程中，学生难免会因自身知识储备不够丰富、数学解题思维不够灵活等而出现错误。此外，一些学生会在相似的题目上重复犯错。为此，小学数学教师有必要探析学生解题错误的根本原因，同时基于根本原因采取相应的优化措施，从根本上解决学生解题错误的问题。

一、小学生解题错误归因

（一）基础不牢固造成解题错误

目前在数学解题过程中，小学生存在错误地判断问题考点、错误地应用数学概念、错误地套用数学公式等问题，最终导致答题错误。究其原因，在于小学生并未牢固掌握基础知识[1]。例如，在北师大版数学四年级（上册）“除法”一课的习题教学中，有问题如下：张老师带领21名学生游湖，每条船能够坐4人，要使学生全部坐上船，一共要租几条船？这一问题涉及除法算理、有余数的除法算法等基本知识点。然而，有的学生基础知识不牢固，不能明确总人数与船载人数之间的数量关系，无法列出正确的算式；有的学生由于对算理、算法掌握不牢，在列出算式后计算时出现错误答案。

（二）方法不灵活造成解题错误

小学数学内容丰富，题目形式变化多端[2]。小学生只有灵活应用不同的解题方法，才能够正确解决数学问题。但是，部分学生在解题时存在惯性思维的问题，如解题思路同质化，解题方法套路化等，不能以灵活的思维探究数学问题，最终出现解题错误。例如，

在北师大版数学四年级（上册）“运算律”一课的习题教学中，有问题如下：用简便算法计算98×32的结果。在解答这一问题时，很多学生将98拆分为90+8，将32拆分为4×8，但仍然难以进行简便计算，反而增加了计算量，容易造成计算错误。究其原因，在于这一算式并未以符合乘法交换律、乘法结合律、乘法分配律的一般形式出现。然而，部分学生习惯直接套用a×b×c=a×c×b、a×（b+c）=a×b+a×c等公式解决25×32×4、125×97×8等形式规范的数学问题，不能对另外形式的问题进行拓展思考，最终造成解题错误。

（三）做题不检查造成解题错误

小学阶段，不乏知识基础扎实、能力水平良好的学生[3]。但这类学生在解决数学问题时仍然会出现错误。例如，学生对三位数除以两位数的算理、算法掌握十分扎实，且能灵活应用试商方法，但由于计算时代错数值，忘记退位，最终导致解题错误。由此可以发现，

部分学生具备正确答题的能力，但由于自身马虎、不认真而未能正确计算，也未能自我纠查出错误。

二、避免小学生数学解题错误的教学对策

（一）筑牢基础，扫除解题障碍

1.趣味教学讲解知识，提升解题认知

数学知识具有一定的复杂性与抽象性。小学数学教师应根据小学生的认知发展特征合理优化教学方法，如采取情境、游戏等趣味教学方法，融入故事、视频等趣味教学元素，调动学生的理论学习积极性，使学生在主动学习的过程中理解知识，进一步提升学

生的认知水平，为学生正确分析问题、解答问题奠定基础。

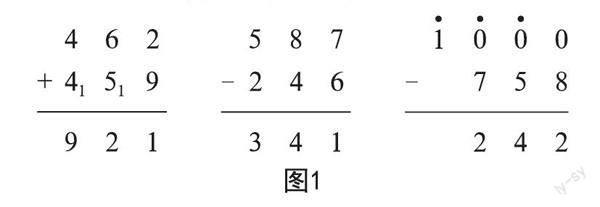
例如，在北师大版数学二年级（下册）“加与减”一课的解题教学中，为了让学生能夠明确462+459、587-246、1000-758等计算问题所考查的知识点，顺利运用正确知识解决问题，教师需要先让学生理解三位数加三位数（包括进位加）、三位数减两位数、三位数（包括退位减）的算理与算法，帮助学生奠定解题基础。但是，相关计算原理具有一定的抽象性，学生在计算时容易忘记进位或退位，造成计算错误。要想让学生快速理解相关知识，教师可以采取游戏教学法为学生讲解计算原理。例如，教师可以在课内组织“卡片游戏”：教师不断出示带有数学加减法问题的卡片，能快速说出答案的学生晋级，剩余学生淘汰。之后，教师依次出示700-200、500+400等几百加、减几百问题的卡片，700-50、150-70、300-150等几百几十加减几百几十的问题卡片，985-251、321+123、245-105等几百几十几加减几十或几百几十几的问题卡片，组织学生快速抢答。此外，教师还可针对淘汰学生组织“复活赛”，让他们翻阅教材、笔记，回想算理、算法，之后再为他们出示相应题卡，正确解决题卡问题最多的学生可以“复活”，继续参加比赛。所有学生均可在“卡片游戏”中思考相关算理、算法，巩固算数知识基础，

提高运算能力。完成游戏教学后，教师再对游戏结论进行总结：三位数加（减）三位数时，要保证被减数、减数相同数位对齐，不同位数分别相加减，并将得数落在相应数位上，如果有进位则加1，如果有退位则减1。在此基础上，教师再出题并引导学生应用具体算理、算法解决问题（如图1），有利于学生根据算理、算法正确列出竖式并计算出问题答案。

2.拓展教学，渗透数学思想，丰富解题内涵

将数学思想渗透进小学数学课程教学中，有利于拓宽学生的数学学习视野，丰富学生的解题思路。在完成基础知识教学后，教师可以围绕课程教学主题收集、整理相应的数学思想教学内容，之后通过例题呈现的方式为学生渗透数学思想，指导学生在解答例题、剖析例题的过程中感悟数学思想方法的奥妙，使学生学会应用不同的数学思想与方法解决问题。

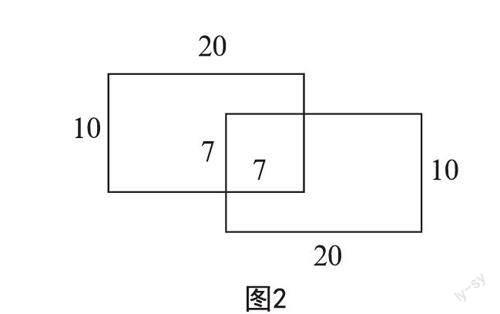
例如，在北师大版数学三年级（上册）“周长”一课的解题教学中，有一个比较复杂问题的如下：图中不规则图形是两个长方形组合在一起的，求这个图形的周长。

这其实是一道非常规的求图形周长的问题。学生多会按照普通方法求解问题，先求出不同部分线段的长度，之后将不同部分线段长度相加，不仅计算步骤烦琐，还容易在计算中出错。针对这一问题，在进行解题教学时，教师可以先为学生渗透转化思想：转化思想是化复杂为简单，化含糊为明朗的一种数学思想。在解决数学问题时，我们可以先观察题目特征，分析题目中的问题是否可以转化为更加直观、更加明朗的问题，之后用更加简单的方法解决问题。

说明转化思想的内涵后，教师可以指导学生应用转化思想解决此数学问题：“根据转化思想，我们可以使用移补的方法将复杂的不规则图形转化为标准图形，如三角形、正方形、平行四边形、长方形等。根据原题内容，我们可以应用转化思想将组合图形移补成新的标准图形——长方形。此长方形的长为20+20-7=33，宽为10+10-7=13。之后，我们可以使用求图形周长的计算公式求得移补后标准图形的周长：（33+13）×2=92。”

这样，教师通过拓展教学，渗透转化思想，可以让学生掌握化复杂为简单的解题方法，从而提高学生的解题效率。

（二）活跃思维，提升正确解题能力

机械套用数学公式、数学模型是导致学生错误解题的主要原因之一。学生之所以机械套用数学公式，是因为未能理解数学公式本质。为此，教师可以在小学数学教学中组织专项习题练习，通过一题多变、一题多解练习，加深学生对类型问题的理解，使学生明确数学公式、数学模型本质，掌握合理分析问题及合理应用数学公式、数学模型的要领，从而提升学生解题能力。

1.在练习中组织一题多变活动，提升分析能力

在小学数学解题教学中组织一题多变教学活动，可以让学生有更多迁移练习的机会，从而提升学生的数学分析、数学迁移、数学应用等能力。在具体练习中，

教师可以先围绕课程教学主题搜罗典型例题，之后围绕典型例题设计变式问题，组织学生在课上解答题组。

例如，在北师大版数学五年级（上册）“多边形的面积”一课的解题教学中，针对本课教学内容，教师可以搜罗以下应用例题。

例题：有一批圆木堆成梯形，最上面一层有3根，最下面一层有8根，相邻两层相差1根，一共堆了6层，这堆圆木共有多少根？

根据例题给出的信息，可以将求圆木根数的问题转化为求梯形面积的问题，之后套用计算公式S梯形=（上底+下底）×高÷2进行解答，得到这堆圆木共有33根的答案。

为了让学生进一步理解此类问题的内涵，教师还可以设计类似问题，供学生分析、思考、探究。

变式1：一堆钢管，最上层5根，最下层10根，每相邻两层差1根，一共有6层，这堆钢管一共有多少根？

变式2：一堆钢管，最上层1根，最下层11根，每相邻两层差2根，一共有6层，这堆钢管一共有多少根？

变式1仍可看作求梯形面积的问题，变式2可以看做求三角形面积的问题，可以分别应用面积求解公式S梯形=（上底+下底）×高÷2与S三角形=底×高÷2解决问题。完成变式问题教学后，教师可以让学生讨论不同问题的解题过程，让学生在讨论过程中进一步锻炼问题分析能力。

2.在练习中落实一题多解，发展多元思维能力

在实际教学中，教师可以分析本课教学内容与其他课程教学内容的关联，之后综合不同知识点的关联设计解题方法多样化的数学问题。教师可以组织学生应用不同的方法解决问题，并鼓励学生分享不同解法，使学生在思考、运算、分享的过程中认识到数学解题方法的不唯一性，从而发展多元解题思维能力。

例如，在北师大版数学六年级（上册）“比的认识”一课的解题教学中，教师可以综合本课教学内容、过去教学内容设计问题：如果有140个橘子，按照3∶2分应当怎样分？之后，组织学生以小组为单位讨论问题，让学生通过讨论发展多元解题思维能力。

生1：可以先将橘子平均分成5份，之后按照比例相乘，算出不同部分橘子数量，具体计算过程如下：140÷（3+2）＝28（个），28×3＝84（个），28×2＝56（个）。

生2：可以先将橘子平均分成5份，之后先计算出“3”比例份额的橘子数量，之后用总数量减去“3”

比例份额的橘子数量，得到“2”比例份额橘子数量，具体计算过程如下：3+2＝5，140÷5＝28（个），28×3＝84（个），140-84=56（个）。

生3：可以将比例问题转化为分数乘法问题，具体计算过程如下：3+2＝5，140×3/5=84（个），140×2/5=56（个）。

这样，教师先通过呈现具体问题激活学生的解题思维，之后组织学生围绕问题展开讨论，能使学生在思考问题、分析问题、讨论解法的过程中学会综合应用加、减、乘、除等多种方法解决问题，形成多元解题思维能力。

（三）培养习惯，培养纠错改正素养

教师应以平常心看待学生的解题错误，并采取恰当的方法培养学生纠错、集错的学习习惯，以此发挥

“错误”的育人价值，避免学生再次犯相同的错误。为此，教师应在小学数学解题教学中积极组织习题检查活动、习题纠错活动等教学活动。在活动中规范学生的解题行为，逐渐培养学生自我查错、自我纠错、自我改错的习惯，提升学生的正确解题素养。

结  语

综上所述，造成小学生数学解题错误频频的根本原因主要在于学生对基础知识的掌握不够充分、解题思维不够灵活、未养成检查的习惯。教师只有明确学生的根本错误原因，并基于此采取针对性的教学对策，才能有效矫正学生错误的思维习惯，提高学生审题、解题的准确率。为此，教师应不断提升自身专业教学素养，坚持问题导向，明确学生的根本错误原因，同时针对学生的错误原因采取有效的教学对策，弥补学生的学习漏洞，矫正学生错误的解题思维习惯，培养学生分析问题、解决问题的能力，提高小学数学教学质量。

[参考文献]

吴杨.小学数學高年级问题错因及矫正措施思考[J].小学生，2022（12）：49-51.

缪莉莉.以“错”为师 以正认知：小学数学课堂中的错题转化对策[J].教育界，2022（21）：56-58.

刘红红.小学高年级数学系统化错题教学环节分布策略[J].读写算，2022（31）：111-113.

作者简介：黄美珠（1978.12-），女，福建南安人，

任教于南安市梅山中心小学，一级教师，本科学历。