考虑故障弃风影响的海上风电场集群MTDC系统规划

秦少茜，瞿晟珉，宋明阳，王启国，黄玲玲

（1.上海电力大学电气工程学院，上海 200090；2.国网枣庄供电公司，山东枣庄 277000）

0 引言

近年来，随着海上风电技术与产业的发展与成熟，海上风电已成为我国实现清洁能源转型和“双碳”目标的重要内容[1]。海上风电场的建设与开发逐渐向规模化、集群化、深远海化的方向发展[2-3]，分布在深远海域的大容量风电功率如何经济、可靠地接入陆上电网已经成为大规模海上风电场集群开发需要解决的关键问题之一。

多端直流（Multi-terminal Direct Current，MTDC）输电技术由于具备直流输电在远距离、大容量风电功率传输中优良的经济性、可控性等优势，被认为是解决远距离大规模风电集群高效经济并网的有效手段之一。在拓扑结构方面，MTDC 主要有放射形、星形、环形和网状结构等典型拓扑[4]。文献[5]提出一种适用于可靠性要求较高的带中央环形的海上风电场放射形拓扑结构。文献[6]从经济性角度分析了MTDC 输电系统的陆上环形、海上环形、常规环形3种网络拓扑结构，通过算例分析发现常规环形的经济性最优。以往研究大多从可靠性和经济性角度对MTDC 系统拓扑结构进行方案比选，较少有学者针对海上风电场集群MTDC 系统的规划建模和优化方法开展深入研究。一方面，海上风电场集群MTDC 系统成本高昂，合理的规划能够有效降低系统建设的投资成本；另一方面，MTDC 系统规划涉及换流站选址定容、网络拓扑优化、直流海缆选型等多个优化问题，建模过程复杂。因此，有必要对海上风电场集群MTDC 系统的规划建模开展相关研究。

此外，不同于陆上风电场电气系统，海上风电场电气系统存在运行环境恶劣、可及性差、故障维护时间长等缺点，其发生故障带来的弃风损失远高于陆上风电场。现有海上风电并网工程在进行规划时一般按照额定容量进行设备选型，一旦并网系统发生故障将造成高昂的弃风损失。充裕的换流站功率设计和合理的直流网络拓扑设计，能够满足较大范围的风电功率波动需求，在故障情况下减少弃风。但系统冗余的增加也会导致系统投资成本相应增加。因此，大规模海上风电MTDC 系统规划设计，是一个需要兼顾投资成本与故障条件下弃风损失的综合优化问题。

因此，本文围绕大规模海上风电集群MTDC 系统的规划问题展开研究，主要讨论大规模海上风电的MTDC 并网系统在故障条件下的设备选型、直流拓扑选择与弃风损失之间的相关性，提出了一种考虑MTDC 网络拓扑变化的弃风率指标，并在此基础上，构建了一种包含MTDC 系统投资成本与系统故障弃风率指标的双目标优化规划模型。算例针对容量为2 000 MW 的海上风电场集群MTDC 接入方案进行优化与分析，结果表明本文构建的双目标优化模型，能够在保证投资经济性的条件下降低系统在故障情况下的弃风率，为工程设计提供参考。

1 MTDC系统弃风损失模型

一般来说，弃风率与陆上电网消纳能力和设备故障后系统功率传输能力等因素相关[7-9]。本文基于海上电气设备的故障概率统计数据，考虑海上换流站与直流电缆的故障，结合图论的图与子图概念，构建MTDC 系统故障条件下子拓扑网络，根据子拓扑网络发生的概率与子拓扑网络传输能力不足导致的弃风功率，提出了一种适用于MTDC 系统的弃风率计算模型，具体流程如图1 所示。

图1 系统故障条件下弃风率计算流程图Fig.1 Flow chart for calculation of wind power curtailment ratio under system fault conditions

1.1 MTDC系统最大输出功率计算

MTDC 系统的网络拓扑结构具有多样性[10-11]，为了直观地描述直流电缆与换流站之间的连接关系以及海上直流网络拓扑对海上风电经MTDC 系统并网规划方案的影响，定义一种MTDC 网络拓扑连接矩阵AT：

式中：m为直流电缆的数量；n为换流站数量；AT为m×n矩阵；αTlp为矩阵中元素。若αTlp=0，表示第l条线路与节点p不相连；若αTlp=1，表示第l条线路与节点p相连且支路电流方向为流出该节点；若αTlp=-1，表示第l条线路与节点p相连且支路电流方向为流入该节点。

对任意一个MTDC 系统网络拓扑AT来说，当系统中某一个换流站或者直流电缆退出运行后将剩余拓扑定义为子拓扑，因此，拓扑AT可以分为a个子拓扑（a为换流站与直流电缆数量之和），子拓扑对应的连接矩阵为ATt。

假设MTDC 系统中直流母线电压矩阵为Udc、直流母线电流矩阵为Idc、直流网络子拓扑连接矩阵为ATt。由此可以得到直流网络子拓扑的直流电缆额定功率矩阵Plineo，具体表达为：

式中:⊙为Hadamard product 矩阵运算符号；Y为导纳矩阵。

其 中，Plineo=[Plineo1，Plineo2，…Plineom]T，Udc=[Udc1，Udc2，…Udcn]，Idc=[Idc1,Idc2,…Idcm]。

MTDC 系统的控制策略主要有下垂控制和主从控制2 种。基于下垂控制策略的MTDC 系统，采用多个换流站共同承担功率平衡与直流电压控制的任务，可由多个基于下垂控制策略的换流站（下垂站）共同应对系统中各种功率不平衡状况，单个换流站的容量裕度小于主从控制策略下的主站，且在故障情况下仍然具有一定的功率与电压平衡控制能力，因此本文的MTDC 系统基于下垂控制策略展开研究。

由MTDC 系统的下垂控制特性可知，直流母线电流与下垂站有功功率的关系可表示为：

式中：Pref为换流站的有功功率参考值矩阵；Udcref为直流母线电压参考值矩阵；Kdroop为下垂系数矩阵，是一个对角矩阵；./为矩阵对应元素相除。

联立式（3）和式（4）即可得到直流电压和换流站功率的关系。由于该数学模型为一个隐式函数，因此将直流电压和换流站功率计算表示为：

式中：f1为直流电压和换流站功率的隐函数。

联立式（2）和式（5）可得到直流电缆额定功率与风电场集群输出功率的关系：

式中：Ptr为直流系统传输功率矩阵。

将直流电缆额定功率Pline带入式中，并利用智能算法求解即可得到子拓扑e的最大输送功率

1.2 故障情况下MTDC系统弃风率指标

通过式（6）可计算出MTDC 系统中每一个子拓扑的最大输送功率，而风电场集群额定功率与MTDC 系统子拓扑最大输送功率之差即表示该子拓扑的弃风量。因此，MTDC 系统子拓扑的弃风率可表示为：

式中：γe为第e个子拓扑弃风率；Pwf为海上风电集群总功率；pr,e为第e个子拓扑换流站或直流电缆的故障概率；Trep,e为第e个子拓扑换流站或直流电缆故障修复时间；Teq为风电场等效运行小时数。

根据式（7）可得到MTDC 系统故障情况下弃风率指标为：

式中：γ为弃风率。

2 考虑故障弃风影响的海上风电场集群MTDC系统优化模型

2.1 目标函数

以系统投资成本和弃风率最小为目标，构建海上风电集群经MTDC 系统接入陆上电网的双目标优化模型，并对MTDC 网络拓扑、换流站容量等变量进行优化，目标函数如式（9）所示：

式中：目标函数F为AT拓扑的综合目标；目标函数F1为拓扑AT下的海上MTDC 系统的投资成本，主要包括换流站成本Ccon、直流电缆成本Ccab；目标函数F2为拓扑AT下的弃风率；A为网络拓扑集合。

郭文安：教材编写往往被人看成是对学科基础知识的编排与阐述，对有关科研成果的概括和整理，因而不受重视，甚至不被看作是一种科学研究。教材编写与科学研究确有所区别，前者主要是在已有科研成果基础上进行的。但是，二者亦有共同点，教材编写同样具有探索、研究、整合与创新的属性，实质上也是一种科学研究。因为一本好的教材应有广博、坚实、精深的专业知识。它不应限于概括与整理已有的科研成果，在学科理论的简明化、系统化和体系化上都应有新的突破、发展与提高。它应兼具专业性、基础性、学术性和前瞻性。它可使广大师生及读者受益匪浅，获得进一步探究的依据与动力。可以说，一本好教材其价值并不亚于一本好专著。

2.1.1 换流站成本

换流站的成本主要考虑换流阀的设备成本、平台的建设安装成本以及换流站配套电气设备与控保装置等费用[12-15]。根据文献[16-17]，换流站成本以额定功率进行折算，因此换流站的成本可表示为：

2.1.2 考虑故障弃风的MTDC系统直流电缆成本模型

直流电缆成本取决于电缆的选型。对于MTDC系统直流电缆来说，不仅需要满足MTDC 系统正常运行时功率需求，还需要满足在系统故障情况下MTDC 系统功率传输需要。考虑系统故障弃风的直流电缆选型方法具体步骤如下所示：

1）根据陆上最优潮流计算确定陆上换流站最佳运行点，然后依据式（2）计算得到MTDC 系统正常运行时直流电缆h的传输功率Ptr,h。

2）当换流站发生故障后，MTDC 系统可分为n个子拓扑，每个拓扑对应的连接矩阵为{ATt1，ATt2，…ATtn}，并分别计算每个子拓扑中各个直流电缆的传输功率，此时直流电缆的传输功率为：

式中：Pline,h0为MTDC 系统正常运行时第h条直流电缆传输功率；Pline,h为MTDC 系统故障情况下第h条直流电缆传输功率。

若直流网络中第h条直流电缆传输功率大于直流电缆最大传输功率Pline,max时，则需要对第h条直流电缆输电容量进行限制，即第h条直流电缆选择电缆最大传输功率：

直流电缆成本主要取决于直流电缆的长度和额定功率，由式（2）计算可得到直流电缆额定功率，直流电缆长度则由网络拓扑矩阵确定，因此直流电缆成本可表示为：

式中：ldc,h为第h条直流电缆的长度；cdc,k,h(Pline)为传输功率为Pline的k型号h直流电缆单位成本。

2.2 约束条件

本文所提优化模型应满足以下约束条件。

1）功率约束。为保证系统正常运行，陆上换流站额定功率之和应大于海上换流站额定功率之和：

当直流组网采用下垂控制策略时，可由多个下垂站进行功率平衡。因此，对于陆上换流站来说，其功率需要满足在任意陆上换流站退出运行后，多个下垂站的功率裕度满足不平衡功率的需求，其功率约束如式（15）所示：

式中：为第g个陆上换流站额定功率。

2）节点电压约束为：式中：Uimin，Uimax为直流母线电压下、上限，i∈AT表示AT拓扑中的第i个直流母线节点。

3）换流站额定功率约束。换流站额定功率配置需满足陆上最优潮流的最佳运行点需求，即换流站额定功率下限，同时不应超过换流站额定功率上限，因此换流站额定功率约束表示为：

式中：为第g个换流站额定功率上限。换流站额定功率上限可由直流网络的输电功率确定，即换流站额定功率上限取决于与之相连的直流电缆的输电功率。因此根据计算的直流电缆功率确定换流站额定功率上限：

式中：Pline,g,h为与第g个换流站相连的第h条直流电缆的传输功率。

3 模型求解

考虑故障弃风影响的海上风电场集群MTDC 系统规划是一个具有多个复杂约束的双目标优化问题。目前，求解多目标优化算法主要分为传统优化算法和智能优化算法2 大类。本文采用非支配性遗传算法NSGAII[18-21]进行求解，是一种基于Pareto 最优解的多目标优化算法。该算法收敛速度更快，计算复杂度低，无需人为设置子目标的权重，但是无法有效处理带约束条件的多目标优化问题，因此本文引用文献[22]中基于优势可行解处理技术（Superiority of Feasible Solutions，SF）技术，解决目标函数的约束问题，改进NSGAⅡ算法中的支配关系，并对本文所提优化模型进行求解。计算流程如图2 所示。

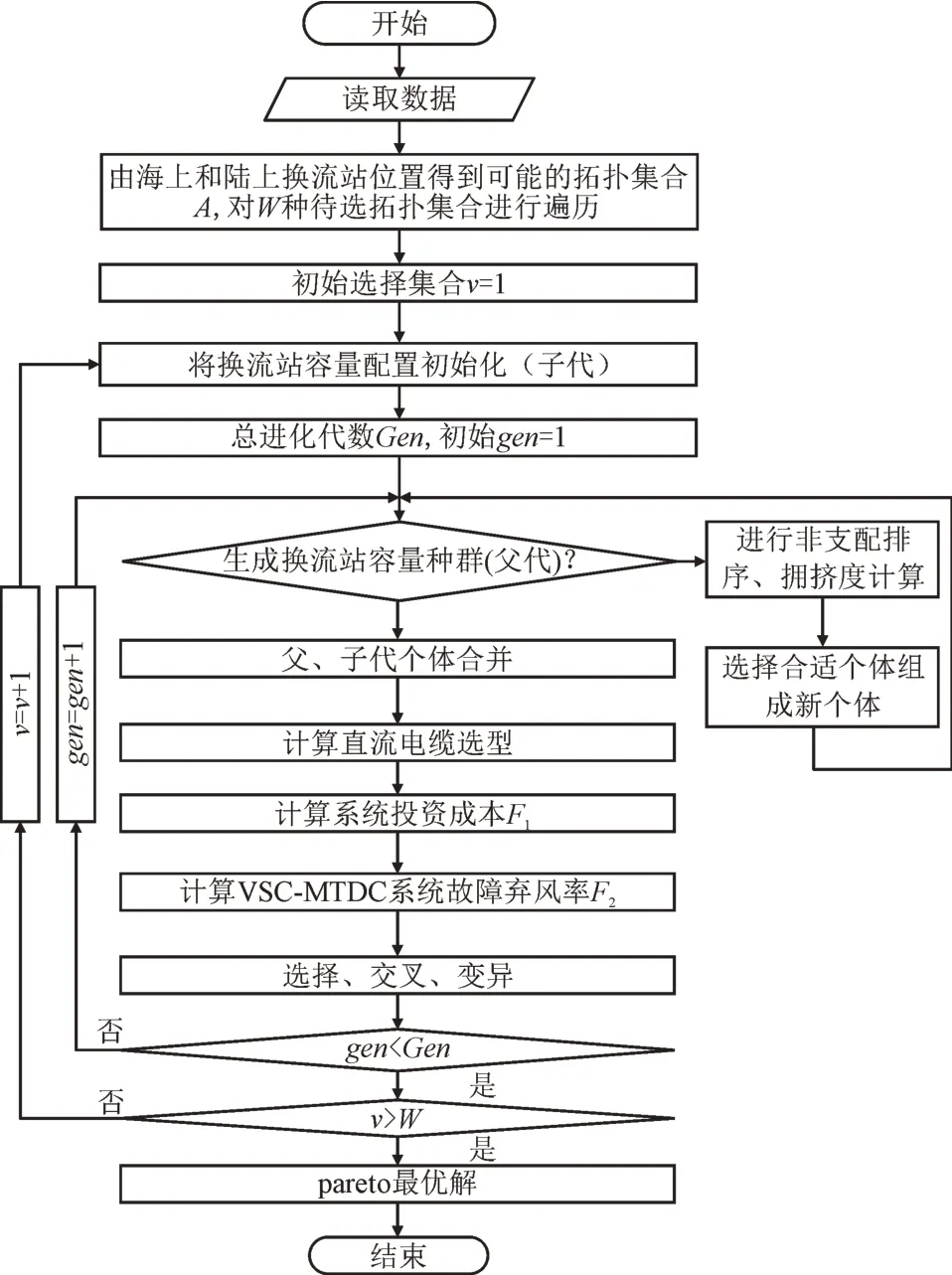
图2 计算流程Fig.2 Calculation process

4 算例分析

4.1 算例介绍

为了验证本文优化模型的有效性，构建了一个海上5 端直流输电系统，其中2 个海上换流站及3 个陆上换流站，2 个海上风电场的容量均为1 000 MW，并根据文献[23]确定海上换流站的位置及容量。陆上公共连接点（Point of Common Coupling，PCC）位置由设计院提供。本文中的设备成本数据使用文献[24-25]中的数据，根据参考文献[26-27]可知MTDC 系统的故障参数。

4.2 最优方案

根据本文优化模型与方法对算例进行优化求解，得到最优规划方案（PT2），MTDC 系统及其与陆上交流电网的连接拓扑如图3 所示。其中，WF1,WF2 分别为2 个海上风电场，黑色阿拉伯数字为线路编号，红色带G 圆圈表示陆上电网。其中换流站最优容量配置如表1 所示，直流电缆最优选型如表2 所示。

表1 换流站最优容量配置Table 1 Optimal capacity allocation of converter stations

表2 直流电缆最优选型Table 2 Optimal selection of DC cables

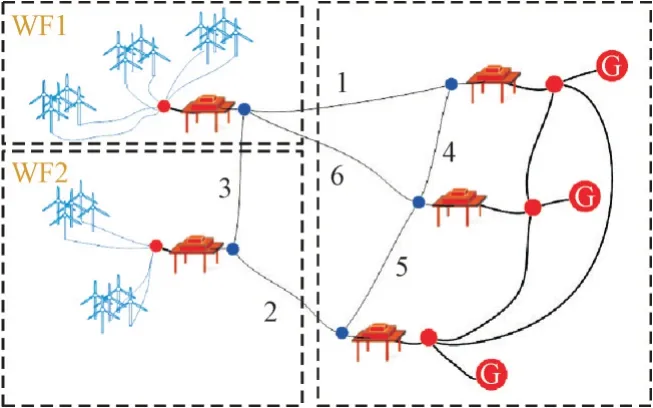
图3 最优规划方案PT2Fig.3 Optimal planning scheme PT2

4.3 结果分析

从MTDC 系统网络拓扑对规划方案选择的影响角度展开分析，根据图论理论中最小连通图的定义，即对于M个节点的连通图，其最小连通图的度为M-1，可知具有N个换流站的MTDC 系统形成最小连通图的直流海缆数量为N-1。当MTDC 系统的直流海缆数量大于N-1 时，则产生拓扑冗余。因此，从直流海缆数量冗余角度定义MTDC 系统的冗余度：

式中：r为拓扑冗余度；Nc为直流海缆数量。

从拓扑对弃风率和投资成本的影响角度展开分析，选取与最优方案拓扑PT2相似但拓扑冗余度不同的2 种拓扑PT1和PT3，并与PT2进行对比论证分析，如图4 所示。根据拓扑冗余度计算，3 种拓扑冗余度大小关系有：r(PT3)>r(PT2)>r(PT1)。

图4 MTDC系统网络拓扑Fig.4 MTDC system network topology

4.3.1 拓扑冗余度对弃风率的影响分析

为了详细说明MTDC 系统网络拓扑对弃风率的影响，分别计算了图4 中3 种拓扑的相对投资成本（以PT3为基准的相对值）及弃风率，如图5 所示。

图5 不同拓扑的投资成本与弃风率Fig.5 Investment cost and wind power curtailment ratio of different topologies

由图5 可以看出：（1）拓扑PT2与PT3弃风率水平相当，皆明显低于PT1；（2）拓扑PT2与PT3较PT1直流电缆的数量更多，投资成本小幅度增加。这是因为，直流电缆选型和换流站容量配置的限制，当规划方案的子拓扑最大输电容量小于风电场集群容量时，增加直流线路可提升网络的输电能力，明显降低弃风率，当子拓扑的最大输电容量大于风电场集群容量时，增加直流电缆将不会影响弃风率。

4.3.2 故障弃风对直流电缆选型的影响分析

为了详细说明考虑故障弃风对直流电缆选型的影响，设计了2 种方案：考虑系统故障弃风（方案A）和不考虑系统故障弃风（方案B），计算了2 种方案的弃风率及系统投资成本如图6 所示。

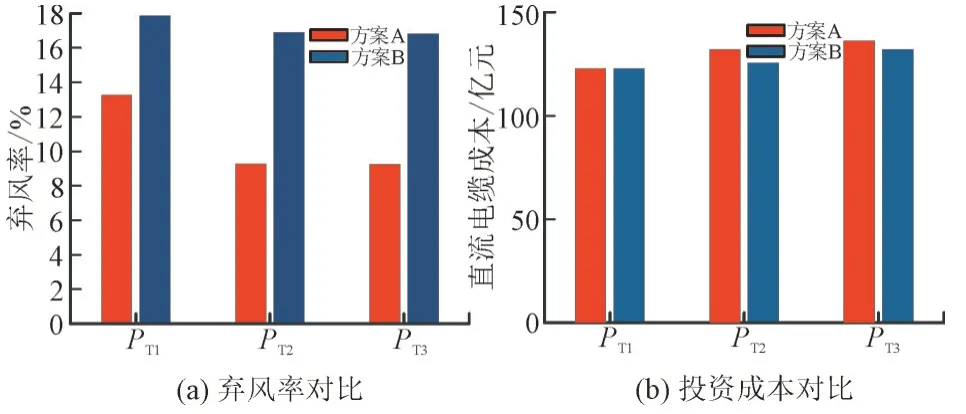
图6 方案A与方案B的弃风率和投资成本对比Fig.6 Comparison of wind power curtailment ratio and investment cost between scheme A and scheme B

由图6 可知：（1）方案A 的投资成本相较于方案B 小幅增加；（2）方案A 的弃风率相比方案B 明显降低。这是因为，方案A 相比方案B 提升了单回直流线路的最大传输功率，因此，方案A 发生故障时形成的子拓扑的最大输电容量更大，从而降低了弃风率。

4.3.3 海上风电场集群容量对投资成本和弃风率的影响分析

为了研究不同容量的海上风电场集群对弃风率的影响，分别计算了图4 中3 种拓扑在不同容量海上风电场集群情况下最优方案的弃风率与投资成本如图7 所示。

图7 弃风率/投资成本随海上风电场集群容量变化情况Fig.7 Variation of wind power curtailment ratio or investment cost with capacity of offshore wind farm cluster

从图7 可以看出：（1）在相同MTDC 系统拓扑结构下，弃风率受到海上风电场集群容量影响。在相同海上风电场集群容量情况下，弃风率受到MTDC 系统拓扑结构的影响。这是因为，拓扑PT1冗余度较小，相比拓扑PT2和PT3子拓扑的输电容量小，因此拓扑PT1随着海上风电场容量的不断增大最先开始增加弃风率；（2）拓扑PT1与PT2，PT3相比，当风电场容量小于1 600 MW 时，拓扑PT1具有较低的投资成本和弃风率，当海上风电场集群容量大于2 000 MW 时，弃风率增加速度明显高于成本增加，并且拓扑PT1的弃风率明显高于PT2和PT3。这是因为，拓扑PT1的冗余度较小，故障情况下子拓扑输电容量无法满足大容量风电功率的全部送出，因此随着海上风电场集群规模的不断增加而产生较高的弃风率。

5 结语

本文研究了考虑故障弃风影响的海上风电场集群MTDC 系统规划方法。计及MTDC 系统在故障情况下由于设备自身容量限制导致海上风电场弃风，提出了一种MTDC 系统故障弃风率指标，可快速计算不同风电装机容量、不同拓扑的故障情况下的弃风率。同时构建了一种考虑海上风电场弃风率和系统投资成本的双目标优化模型，有助于在保证经济性的同时，降低海上风电场弃风率。在MTDC 规划过程中，计及海上风电场集群规模因素优选拓扑，对于小规模风电场集群，优选环形拓扑，对于大规模风电场集群，适当增加拓扑冗余度可有效降低风电场的弃风率。