基于DWT-SOM-HFS的配电台区短期负荷预测研究与应用
2023-07-17朱卫涛邹文文卢耀文
朱卫涛,邹文文,贾 钦,卢耀文,雷 武
(1.国网武威供电公司,甘肃武威 733000;2.兰州交通大学自动化与电气工程学院,甘肃兰州 730070)
0 引言
负荷预测为电力系统的发展规划和调度运行提供必要的参考依据,根据预测时间尺度的不同,一般可分为超短期、短期、中期和长期预测[1]。配电台区的短期负荷预测对配电网的状态检测与精准管理具有重要意义[2]。然而,随着大量新型非线性负荷接入配电网,配电台区用电环境复杂度变高、负荷预测不确定性增加等问题日益明显,准确地预测台区负荷将变得十分困难[3]。因此,如何提升配电台区短期负荷预测精度是一个重要的研究问题。
由于电力负荷数据是受时刻、天气、节假日等诸多因素影响的非平稳时间序列,因此提高负荷预测精度的关键是从负荷样本中提取出高质量的特征信息[4-6]。为此,刘亚珲等人在经验模态分解(Empirical Mode Decomposing,EMD)的基础上,进一步运用K-means 算法对分解后的负荷分量进行聚类,以增强样本时序特征[6]。张江林等人提出一种基于离散小波变换(Discrete Wavelet Transform,DWT)的模糊K-modes 负荷聚类算法,相较于EMD和K-means 的组合算法,该算法具有更好的聚类效果[7]。魏震波等人通过快速傅里叶变换(Fast Fourier Transformation,FFT)获取负荷数据期望频率,并将其作为聚类特征量,然后利用密度层次聚类(Density-based Clustering-Hierarchical Clustering,DC-HC)算法实现负荷聚类[8]。通过分析文献[6-8],可以发现研究合适的负荷分解聚类组合算法对增强负荷特征信息进而提高负荷预测精度具有积极意义[9-11]。DWT作为一种时频分解方法,解决了FFT在非平稳时间序列上的不足,并在低阶近似的方式下实现负荷数据的重构[12]。自组织特征映射(Self-Organizing Map,SOM)作为一种无监督、拓扑保持和强非线性映射的神经网络,其聚类结果具有比较高的可视化和可解释性[13]。因此,本文将DWT与SOM算法组合用于负荷分解聚类。
在预测模型方面,神经网络(Back Propagation Neural Network,BPNN)[14]、支持向量机(Support Vector Machine,SVM)[15]、极限学习机(Extreme Learning Machine,ELM)[16]等机器学习模型得到广泛应用。然而,在面对大量的负荷数据时,单个模型往往预测精度偏低[17],容易过拟合或陷入局部最优解。随着深度学习技术的不断发展,以长短期记 忆 网 络(Long-short Term Memory Network,LSTM)[18-19]和卷积神经网络(Convolutional Neural Network,CNN)[20]为代表的深度学习模型进一步显著提升了负荷预测精度,但是其涉及大量的超参数且网络结构复杂,对计算资源需求高,此外,模型可解释性也一直是其弱项。对此,层次模糊系统(Hierarchical Fuzzy System,HFS)模型通过将多个由IF-TEHN规则构建的FS按层连接在一起,解决了深度神经网络模型在模型可解释性方面的不足,具有很好的应用潜力[21-22]。
综上所述,为进一步提高配电台区短期负荷预测精度,本文提出一种结合DWT,SOM 与HFS 的负荷预测方法,并将其应用于某省某市所属配电台区短期负荷预测实例中,以验证其有效性。
1 DWT-SOM-HFS模型基本原理
1.1 DWT方法
DWT 可将时域中的负荷序列分解为频域中的多个不同分量,其中低频近似分量反映负荷的整体变化趋势,高频细节分量表征负荷的局部波动特征。
若给定长度为N的负荷序列X={X1,…,XN},则采用DWT 对其进行频域分解,表达式为:
式中:Aj,Dj分别为X分解后得到的第j层低、高频分量,其中A0=X;j∈[0,n-1],n为分解层数;h,g分别为分解过程的高、低通滤波器。
相应地,DWT 对负荷序列的重构表达式为:
根据式(1)—式(2),则DWT 分解重构过程如图1 所示,其中A1,A2,…,An-1,An分别为第1,2,…,n-1,n层分解后的低频分量,D1,D2,…,Dn-1,Dn分别为第1,2,…,n-1,n层分解后的高频分量。

图1 DWT分解重构过程Fig.1 Decomposition and reconstruction of DWT
1.2 SOM网络
SOM 神经网络基本结构如图2 所示,其输入层共有s个神经元,由符号I1,I2,…,Is表示,竞争层由t个神经元组成二维单元阵列,通过采用负荷序列经DWT 分解得到的多个频域分量作为输入样本特征,并对其所属模式进行自组织学习,最终将竞争层中的各神经元划分不同的响应区域,从而实现对负荷序列的自动聚类,具体算法过程如下:
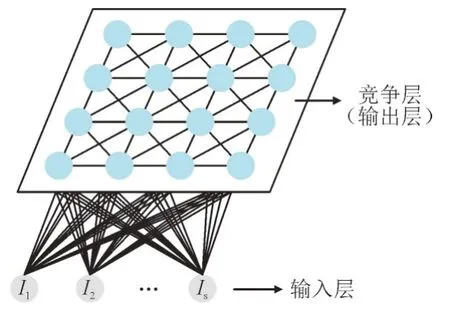
图2 SOM神经网路结构Fig.2 Structure of SOM neural network
1)网络初始化:随机初始化输入层与竞争层各神经元之间的连接权值wbp(b=1,2,…,s;p=1,2,…,t),令迭代次数p=1,设定最大迭代次数为P。
2)输入样本归一化:对输入样本I=[I1,I2,…,Is],进行归一化处理。
3)求取获胜神经元:计算输入样本I与每个竞争层神经元q的连接权值之间的距离dq,其中距离最小的神经元获胜。
式中:Ib为输入样本I的第b个输入特征。
4)修正网络权值:修正获胜神经元邻近区域的神经元权值。
式中:wbq(p)为第p次迭时wbq的值;η(p)为第p次迭代中获胜神经元的邻接函数,其随两神经元间距离的增加而减小。
5)更新输入样本,返回步骤3),直至所有输入样本更新完毕。
6)令p=p+1,返回步骤3),直至迭代次数达到P。
1.3 HFS模型
HFS 基本结构如图3 所示[21],系统初始输入为(x1,x2,…,xn),其中,第l(l=1,…L)层模糊子系统FS通过窗口大小和移动步长可变的滑窗(图中二者都设置为2)在该层输入空间中选择其输入变量,相应层模糊系统的输出为(yl1,yl2,…,yl(n/2))。在第一层模糊系统设计完毕后,采用参数优化算法进行训练,其输出构成第二层模糊系统的输入空间;接着,第二层输出作为第三层输入。以此类推,自下而上分层设计,直至整个HFS 构建完成,系统最终输出为yL1。
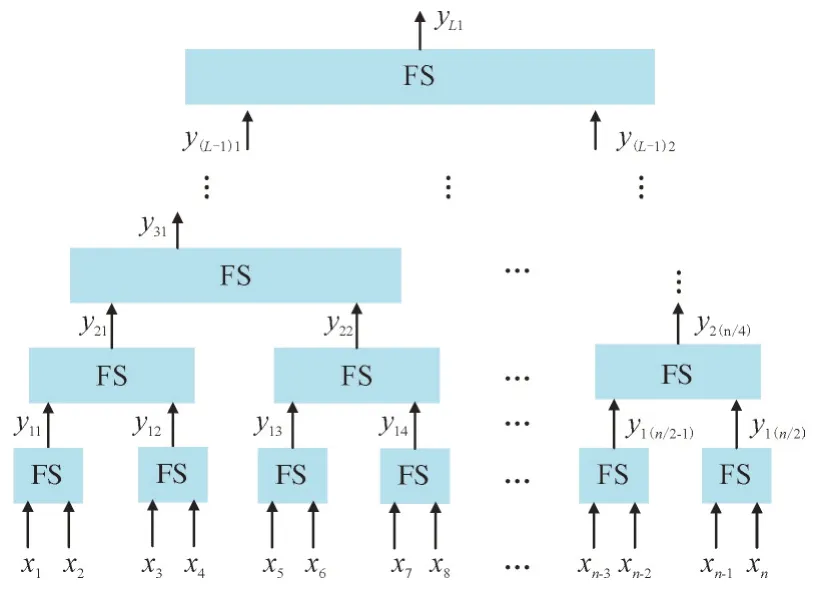
图3 分层模糊系统结构Fig.3 Structure of HFS
若模糊子系统FS 输入为(x1,x2),输出为y11,且对每个输入变量分别定义m,n个模糊集,则FS 可由m×n条IF-THEN 模糊规则所构建,其中第ij条规则Ruleij的表达式为:
式中:IF 为规则前件部分,and 为模糊逻辑“与”,THEN 表示规则后件部分;Mi,Nj为输入x1,x2相应模糊集的隶属度函数;θij为输出y11的模糊集的中心值;i=1,…,m;j=1,…,n;
对于两输入、单输出的FS,其模糊推理过程可由如图4 所示的FS 结构来解释:
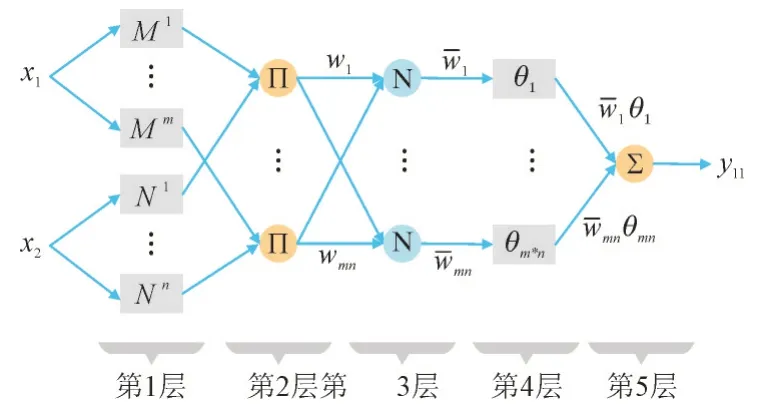
图4 模糊子系统FS结构Fig.4 Structure of single fuzzy system
第1 层:计算输入的隶属度(文中采用高斯型隶属度函数);
式中:c1i,σ1i,c2j,σ2j分别为隶属度函数μMi(·),μNj(·)的均值和标准差。
第2 层:计算每条规则的点火强度(图4 中∏代表不同输入的隶属度连乘);
第3 层:计算每条规则点火强度的归一化值(图4 中N表示归一化);
第4 层:计算每条规则的输出θij;
第5 层:计算模糊系统的输出。
式中:为点火强度wij的归一化值。
在式(6)—式(9)计算过程中,模糊规则前件参数,即隶属度函数参数c1i,σ1i,c2j,σ2j,以及后件参数θij是未知的,采用梯度下降和递归最小二乘算法分别进行训练,具体算法流程参考文献[23]。
2 DWT-SOM-HFS负荷预测模型设计
2.1 DWT-SOM-HFS模型框架
DWT-SOM-HFS 负荷预测模型框架如图5 所示。
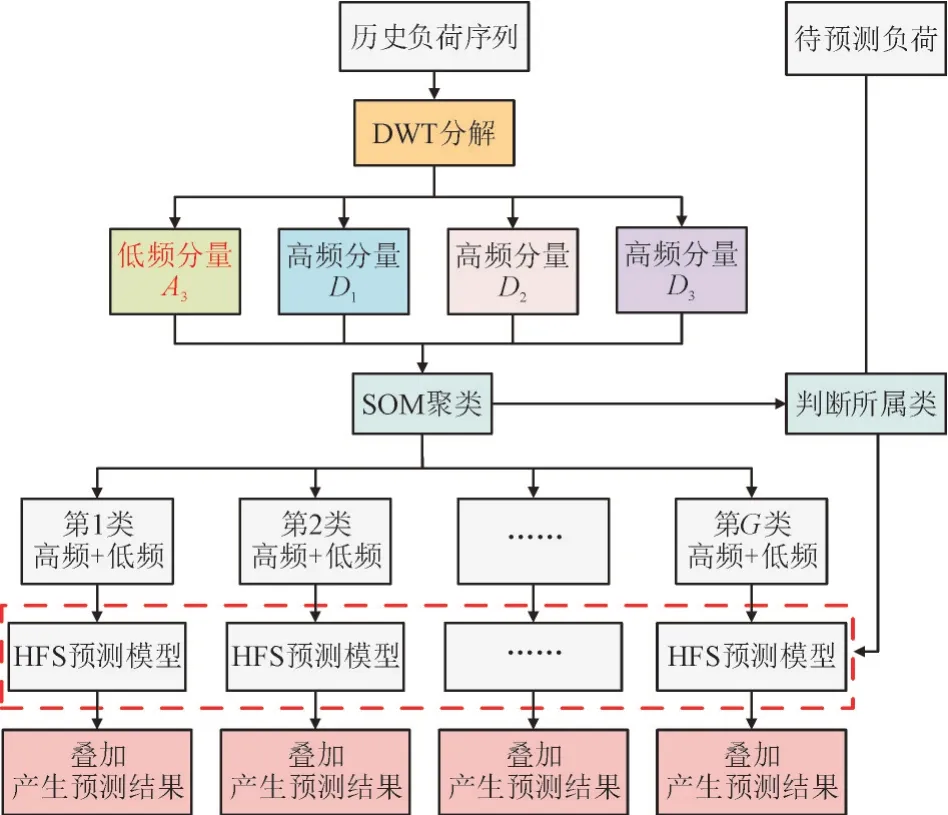
图5 基于DWT-SOM-HFS的负荷预测模型框架Fig.5 Framework for load forecasting model based on DWT-SOM-HFS
首先,采用DWT 将历史负荷序列分解为多个频域分量A3,D1,D2,D3,并将其作为负荷聚类的输入特征;然后,利用SOM 对具有相似特征属性的负荷进行聚类,形成包含各高低频分量的G类数据组;最后,分别对G类数据组的不同分量建立HFS 预测模型。针对待预测负荷,可将其前一时刻的负荷频域分量作为SOM 输入特征,来判断其所属负荷类型,进而选择对应类的HFS 预测模型对不同分量进行预测,并叠加各分量预测值以产生最终预测结果。
由于DWT 进行原始负荷数据分解时,其分解层数为3 层,则其分解后的各频域分量包括低频分量A1,A2,A3和高频分量D1,D2,D3。其中分量A3,D1,D2,D3通过DWT 重构即可得到重构后的负荷数据,具体如图6 所示。由图6 可知,原始负荷数据与重构后的负荷数据之间误差非常小(±2×10-10kW),表明分量A3,D1,D2,D3能够很好地表示负荷时序特征,因此将其作为SOM 网络的输入特征是可行的。
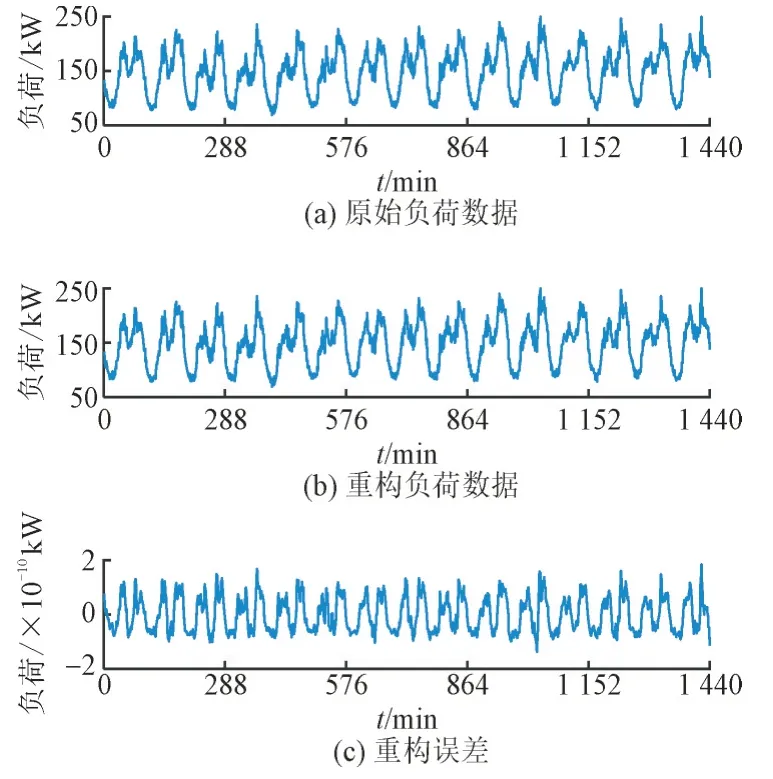
图6 基于DWT的负荷序列重构Fig.6 Reconstruction of load sequences based on DWT
2.2 HFS模型输入
利用HFS 预测当前k时刻的负荷功率时,需要将该时刻前一段历史时刻的负荷数据作为其输入特征。然而,由于历史负荷序列与待预测负荷之间的相关性随滞后步长的增大而减小,因此本文统一确定滞后步长为4,具体地,各频域分量的通用预测模式为:
2.3 预测性能评价指标
为了评估基于本文方法的短期负荷预测模型性能,分别采用平均绝对误差(Mean Absolute Error,MAE)、均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)以及决定系数(R-Square,R2)4 种评价指标,其分别计为EMA,ERMS,ERMS,R。
式中:S为预测点个数;yi为真实值;为预测值;为yi的平均值。
3 算例分析
3.1 数据选取
本文以某省某市所属配电台区2019 年至2021年的负荷数据(采样间隔为15 min)作为实验数据集,其中前2 年用于训练,最后1 年用于测试,对应的每日负荷曲线如图7 所示。
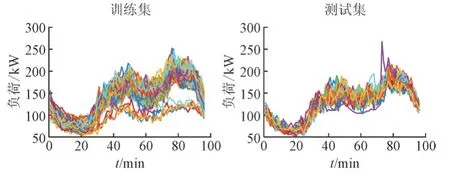
图7 训练测试数据集的每日负荷曲线Fig.7 Daily load curves for training and testing datasets
3.2 数据预处理
为提高模型预测精度,采用四分位法对异常数据进行识别,并对其进行均值修正处理。若定义w为异常数据,则四分位法判断其是否异常的公式为:
式中:Q1和Q3分别为第一四分位数和第三四分位数;IQR为四分位距。
经四分位法分析,实验数据集中的异常数据占比为2.99%。
由于负荷数据波动变化较大,为提高预测模性的通用能力,采用min-max 标准化方式对数据进行归一化处理:
式中:为标准化后的负荷数据;X为标准化前的负荷数据;max(X)为负荷最大值;min(X)为负荷最小值。
3.3 模型参数设置
采用DWT,SOM 和HFS 的组合模型进行负荷预测实验,相关参数设置如下:
1)DWT:分解层数d=3;小波基函数为db4;
2)SOM:最大迭代次数P=200;输入神经元个数s=4,输出神经元个数t=24;
3)HFS:模糊集个数m,n=3;模糊规则前后件参数c1i(0),σ1i(0),c2j(0),σ2j(0),θij(0)(i,j=1,2,3),其初始值在[0,1]间随机生成;学习率γ=0.001;后件参数向量协方差矩阵p(0)=104I9(I9为单位阵);最大迭代次数P=20。
由于SOM 网络输出神经元个数为24,即训练集负荷数据相应被聚为24 类,具体地,各类负荷的功率分布情况如图8 所示。由图8 可知,每类负荷功率值分布在特定区间范围内,这表明DWT-SOM组合方法在负荷数据分解聚类方面效果良好。
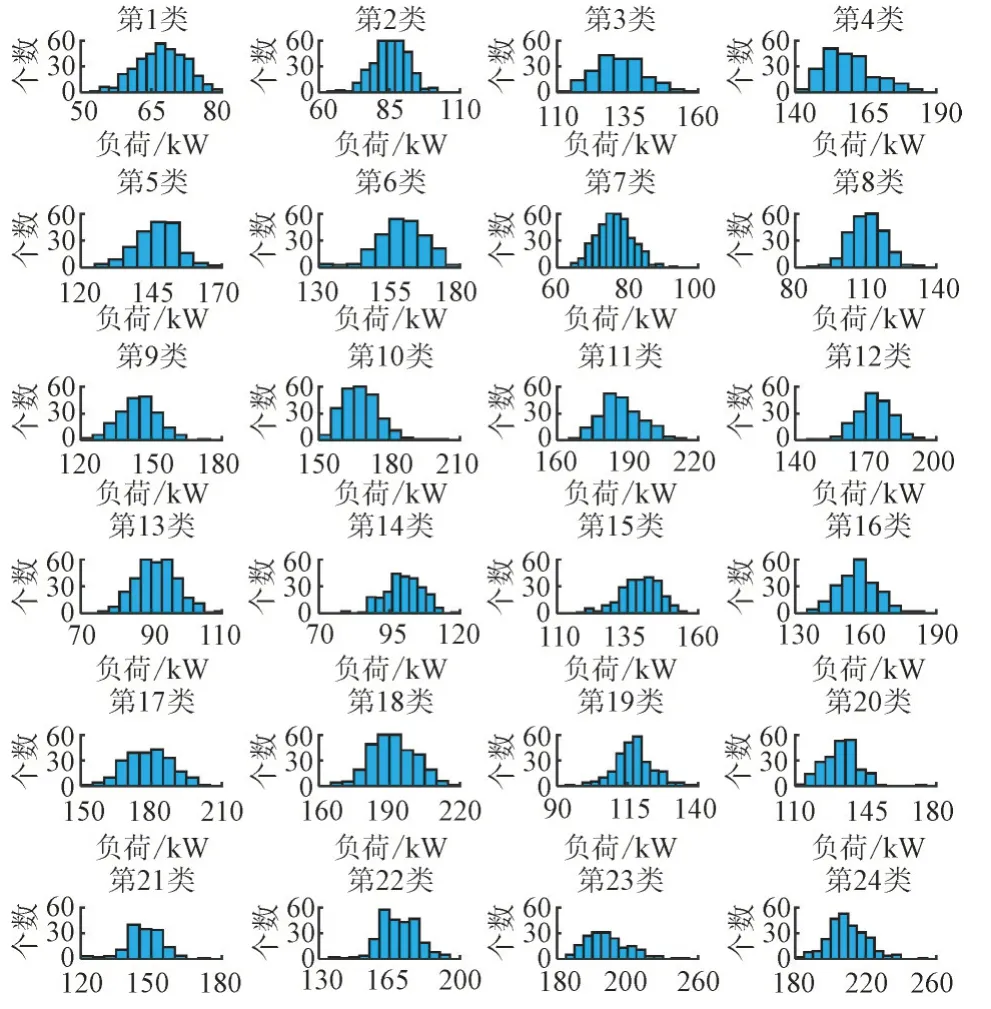
图8 训练集各类负荷功率分布直方图Fig.8 Histogram of load power distribution for each cluster of training datasets
3.4 DWT-SOM-HFS预测性能验证
为验证DWT 频域分解和SOM 聚类对负荷预测的有效性,分别增加了没有经过所提一种或两种数据处理方法的对比模型,具体如表1 所示,其中×代表不含该项,√代表含有该项。

表1 各对比预测模型组合表Table 1 Combination of comparative forecasting models
利用模型M1,M2,M3和M4分别对测试集上的负荷数据进行预测,各模型在某典型日下的负荷曲线预测结果如图9 所示。由图9 可以看出,在负荷序列波动处M4具有更高的预测精度。图10 所示为各模型预测值与负荷真实值间的拟合情况,由图10可以发现,M4综合拟合效果最好。
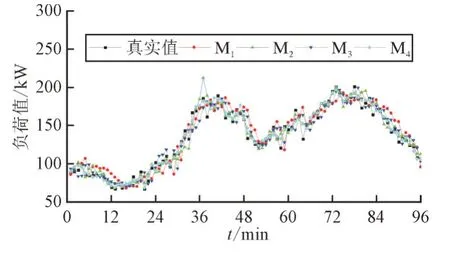
图9 各模型在某典型日下的负荷曲线预测结果对比Fig.9 Comparison of prediction results of load curve between models on a typical day
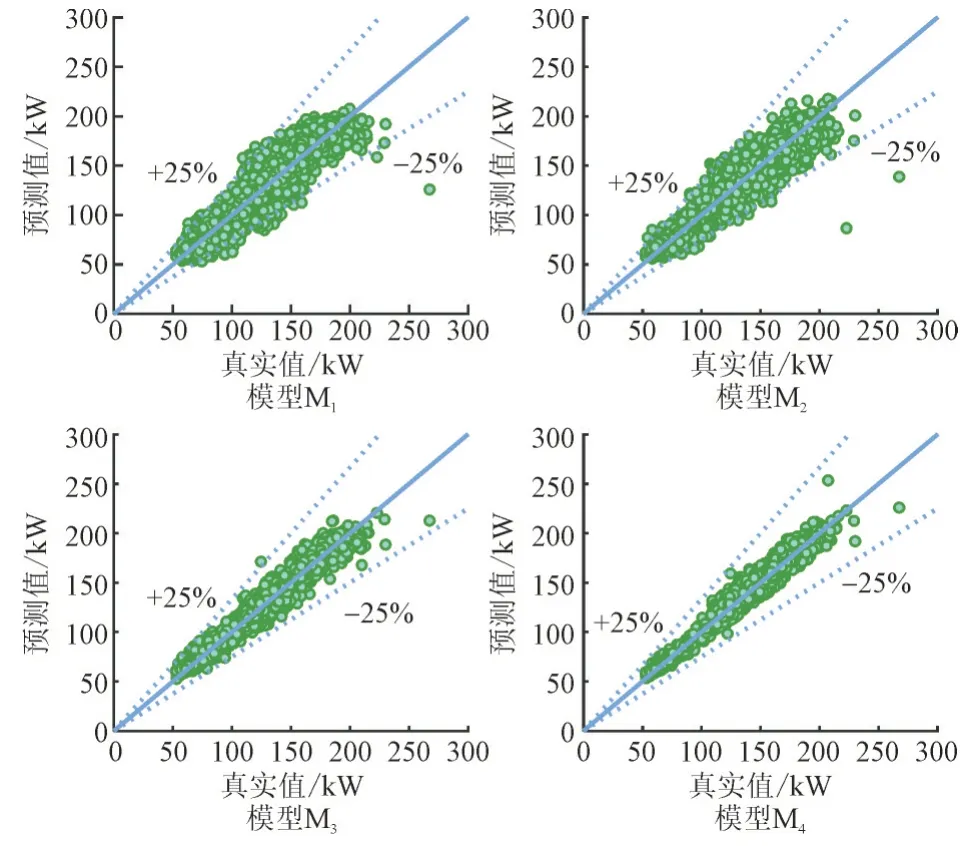
图10 各模型预测值与真实负荷值之间的拟合图Fig.10 Fitting plots of all models between prediction data and real load values
各模型预测性能指标对比如表2 所示。由表2可以看出,采用DWT 和SOM 聚类对原始电力负荷数据进行预处理,再按类分别对各分量进行预测,叠加各分量预测值产生最终预测值,可有效降低负荷预测总误差。其中,M4相较M1,其MAE,RMSE和MAPE 误差指标值分别降低了60.89%,58.60%和63.07%,R2值则提高了12.38%。

表2 各模型预测性能指标对比Table 2 Comparison of forecasting performance indicators between models
为表明HFS 模型的可解释性,表3 给出了其中一类负荷下HFS 中全部模糊子系统FS(上标为层数,下标为个数)所生成的模糊规则前后参数值,其中,c1i,c2j,σ1i,σ2j(i,j=1,2,3) 分别为3 个隶属度函数的均值和标准差,θij为每条规则的输出。在预测时,HFS 第二层模糊子系统通过将第一层模糊子系统,的输出作为其输入,通过更深层的模糊规则表征,来处理输入数据中存在的不确定性(噪声、测量误差等),可进一步提高负荷预测精度。

表3 HFS中所有模糊子系统FS的模糊规则参数Table 3 Parameters of fuzzy rules for all single fuzzy systems in HFS
为进一步验证本文所提方法的合理性,分以下两种情形再次进行对比实验:(1)在采用DWT-SOM算法进行负荷数据分解聚类的前提下,分别选择BPNN[24],SVM[15],ELM[16],RF[25],LSTM[19],CNN[20]作 为预测模型进行预测误差对比;(2)在统一选择HFS为预测模型的前提下,采用不同的分解聚类算法进行预测误差对比,各分解聚类算法特点如表4 所示,其中EMD 与K-means[6],DWT 与K-modes[7]以及FFT 与DC-HC[8]的组合分解聚类算法结合了频域分解和特征聚类算法各自的优势,能够在降低原始负荷数据非平稳性的同时,增强负荷时序特征。

表4 各分解聚类算法特点Table 4 Features of all decomposition and clustering algorithms
表5 给出了所有预测模型的误差评价指标,从平均绝对误差角度看,本文所采用模型HFS 与BPNN,SVR,ELM,RF,LSTM 以及CNN 模型相比,MAE 分别下降了1.995 5,1.672 4,1.214 0,0.700 4,0.372 3,0.505 1;从均方根误差角度看,相对于其他模型RMSE 分别下降了1.388 0,1.206 7,0.897 6,0.690 9,0.237 2,0.490 7;从平均绝对百分误差的角度来看,相对于其他模型MAPE 分别下降了1.388 0%,1.206 7%,0.897 6%,0.690 9%,0.237 2%,0.490 7%。因此,在负荷预测过程中,HFS 具有更高的预测精度。

表5 各预测模型误差评价指标对比Table 5 Comparison of error evaluation indicators between forecasting models
表6 给出了各分解聚类组合算法的误差评价指标,从平均绝对误差角度看,本文所采用DWTSOM 算法与EMD+K-means、DWT+K-modes,FFT+DC-HC 算法相比,MAE 分别下降了1.066 0,0.374 8,0.684 5;从均方根误差角度看,相对于其他算法RMSE 分别下降了0.524 1,0.148 9,0.318 3;从平均绝对百分误差的角度来看,相对于其他算法MAPE分别下降了0.441 3%,0.232 4%,0.368 3%。因此,在负荷数据分解聚类预处理过程中,DWT-SOM 组合算法表现优于其它算法。
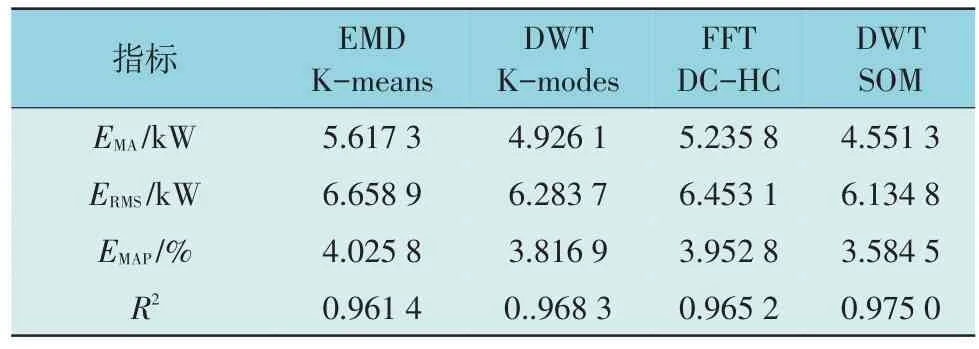
表6 各分解聚类算法预测误差评价指标对比Table 6 Comparison of error evaluation indicators between decomposition and clustering algorithms
通过仿真结果分析可得,本文所提组合预测方法的各项预测误差评价指标均优于其他对比方法,且具有合理的模型可解释性,预测精度更高。
4 结论
本文提出了一种基于DWT,SOM 和HFS 的配电台区短期负荷预测方法,采用DWT 分解负荷序列,将所得到的频域分量作为SOM 网络输入特征,对负荷进行聚类,再对各类负荷频域分量分别使用HFS 进行预测,最后叠加各分量预测值产生最终预测结果。具体结论如下:
1)采用DWT 进行特征提取再利用SOM 聚类的负荷数据预处理手段,可有效提高配电台区短期负荷预测精度。
2)相较深度神经网络,通过IF-THEN 规则构建的HFS 具有可解释性强的优点,并且能够自动调节模型参数,以有效应对负荷预测中存在的不确定性因素,使得预测结果更加可靠。
接下来,研究HFS 模型参数的优化算法以及加入天气、节假日等时序特征是今后工作的重点。
