基于改进三点估计的概率谐波潮流计算

徐艳春，阚锐涵，谢莎莎，MI Lu

（1.梯级水电站运行与控制湖北省重点实验室（三峡大学），湖北宜昌 443002；2.德克萨斯农工大学电气与计算机工程系，美国德州 77840）

0 引言

在能源结构低碳化转型背景下，构建以新能源为主体的新型电力系统将成为实现碳达峰、碳中和目标的重要手段，这使得电力系统从确定性系统向强不确定性系统转变[1]。在源侧，可再生能源发电受到气象条件与环境因素的影响，其出力表现出间歇性与波动性；在荷侧，供需日益频繁，伴随着用户侧光伏与储能的发展[2]，负荷表现出时变性和随机性[3]。新型电力系统中的分布式电源因含有非线性逆变器装置，其给系统带来的谐波问题越来越受到广泛重视[4]。因此，研究不确定性背景下[5-9]的概率谐波潮流对提高电能质量有着重要意义。

概率谐波潮流的研究方法主要分为模拟法、解析法、近似法3 类。蒙特卡洛法[10]（Monte Carlo，MC）在不确定性问题的建模上由于采样数量多、精度高、计算效率偏低，通常被用作衡量其他方法的标准[11]。解析法计算复杂，会造成更大的近似误差，难以求解。而近似法所得结果可近似于真实值，主要以点估计法（Point Estimate Method，PEM）为代表[12]。文献[13]提出一种基于改进的三点估计法和局部电压稳定指标的含风电场电力系统静态电压稳定评估方法。文献[14]分析了不同分布特征的风机在大型传输系统下的概率谐波传播。文献[15]将点估计法与区间仿射法相结合，提供了一种处理背景谐波电压与光伏谐波电流相互作用的方法。但文献[14-15]都为单一谐波源，且输出结果受输入随机变量分布的限制。文献[16]将点估计法与最大熵分布结合，提升了计算效率。

综上所述，目前概率谐波潮流计算的难点在于如何兼顾以下多方面的需求：一是要将输出随机变量的统计特征、概率密度全部求出；二是既要保证计算精度，又要提高计算效率。为此，本文提出了一种基于改进三点估计法与最大熵理论（Improved Three-point Estimate Method and Maximum Entropy，ITPEM&ME）的概率谐波潮流计算方法，以便有效解决概率谐波潮流计算中存在的问题。

本文从概率理论出发，针对配电网中不确定因素导致的谐波问题展开研究：在传统三点估计法基础上通过增加1 组估计点改变原有权重，重新构建风-光-荷的概率模型，避免了引入输入随机变量的高阶矩而造成的较大误差，进而在保证精度的前提下提高工作效率；在所构建的概率模型的基础上引入最大熵理论，对输出变量的概率密度函数进行重构，从而对其分布特征进行精确拟合；在IEEE33 节点系统上分别对不同工况下的谐波潮流进行分析，从改善谐波电压精度方面证明了所提方法的可行性和实用性，可用以提高电能质量[17-18]。

1 改进三点估计与最大熵理论

1.1 改进三点估计

本节从统计特征求取以及概率密度函数拟合两方面对改进三点估计法进行改进，提出一种基于ITPEM&ME 的概率谐波潮流算法，用以分析评估系统状态。

点估计法根据求得的n个风机、光伏和负荷的出力作为输入随机变量Xi(i=1,2,...,n)的m个估计点xi,j(j=1,2,...,m)及权重wi,j，来获得一系列概率分布，估计出待求输出变量谐波电压Z的数字特征。估计点xi,j和权重wi,j如式（1）和式（2）所示：

式中：xi,j为第i个风机、光伏和负荷出力的第j个估计点；μi和σi分别为第i个风机、光伏和负荷出力波动的期望和标准差；ξi,j为第i个风机、光伏和负荷出力的第j个估计点xi,j所对应的位置系数，由风机、光伏和负荷出力波动的标准化中心矩获得。

式中：wi,j为第i个风机、光伏和负荷出力波动的第j个估计点对应的权重。

为了提高谐波电压在期望值处的权重，新增估计点处的新位置系数ξ′i,j及相对应的权重如式（3）所示：

式中：ξ′i,1，ξ′i,2分别为第i个风机、光伏和负荷出力波动的第1，2个估计点的新位置系数；w′i,j为第i个风机、光伏和负荷出力波动的第j个估计点对应的新权重。

新位置系数ξ′i,j忽略了峰度系数λi,3，能够更好地改善尾部特征，因此只需考虑新估计点的权重w′i,j的前3 阶矩即可使计算结果更加精确。

将式（3）中的ξ′i,1，ξ′i,2带入式（1），得到1 组新的估计点x′i,j如式（4）所示：

进而估计待求输出变量谐波电压Z的原点矩E′(Zl)如式（5）所示：

式中：g(Xμ)为风机、光伏和负荷出力取各自数学期望时对应的函数值，反映了风机、光伏和负荷出力与谐波电压之间的非线性关系；μn为第n个随机变量的期望值；w0为当估计点取期望值时对应的权重；l为待求变量谐波电压的原点矩阶数。

所提算法在两点估计基础上额外增加1 组估计点x′i,j构造多重采样点，以实现随机变量统计特征的精确求解，其期望值取自所有函数值线性叠加后的算数平均值。与多点估计法相比，改进三点估计法仅考虑前3 阶矩，避免了计算高阶矩的需求，从而既保证了计算精度，又可避免引入高阶矩，使三点采样更具实际价值。

1.2 最大熵理论

传统点估计（Point Estimate Method，PEM）常与Gram-Charlier（GC）级数展开[19]相结合（PEM&GC）求取输入随机变量的概率密度。针对输出结果统计特性描述的需要，本文通过将改进三点估计与最大熵理论结合对统计特征的求取方面做出进一步改进。

最大熵理论是以Z的熵取最大值为目标函数，以Z的前4 阶原点矩作为约束条件，通过求解非线性方程可获取Lagrange 系数λ0,λ1,...,λ4，最终得到的最大熵概率密度函数如式（6）所示：

式中：fZ(z)为谐波电压Z的概率密度函数；exp 为自然常数e 为底的指数函数；λ0和λl分别为Lagrange系数的初值和第l阶原点矩；zl为Z的第l阶原点矩。

由此可见，最大熵的概率拟合只需要随机变量的前4 阶统计矩作为有限的约束条件。相比于GC级数需要求取随机变量的前7 阶统计矩甚至更多的情况，最大熵理论对未知信息作最少的设定，从而获得更客观的概率分布。

2 概率谐波潮流计算实现框架

2.1 谐波潮流计算模型

电力系统中的谐波源包括传统的非线性设备及现代电力电子装置两大类。当系统中接入分布式电源时，其中存在的非线性电力电子器件通过频繁开关实现电力转换，因而产生一系列谐波分量，其来源如图1 所示。

图1 谐波源来源示意图Fig.1 Schematic diagram of source of harmonic

现有谐波潮流计算方法主要有统一迭代法、交替迭代法、直接求解法和解耦法4 种求解方法。由于谐波潮流是基波潮流在非线性元件中转换产生的，因此基波潮流与谐波潮流两者之间存在相互耦合的关系，计算时可将非线性元件进行线性化处理[20]，由各谐波源节点的注入谐波电流通过谐波网络方程求解各节点谐波电压，如式（7）所示:

式中：Ih为h次谐波电流矩阵；Yh为h次谐波导纳矩阵；Uh为h次谐波电压矩阵。

本文采用解耦法[21]并根据文献[22]所提的谐波潮流模型来求解计及配电网中风-光-荷不确定性的概率谐波潮流问题，在提高计算精度的同时进一步减少计算量。

2.2 基于ITPEM&ME的谐波潮流的计算

假设源荷之间只考虑风速、光照强度及负荷的波动且彼此独立互不干扰。将各节点的负荷需求、风电机组的有功无功出力以及光照强度不同的出力看作输入随机变量，节点电压看作输出变量，带入ITPEM&ME 算法中将不确定性问题确定化。

基于ITPEM&ME 的概率谐波潮流求解流程如图2 所示。其中，k和k′为谐波潮流计算的次数。

图2 基于ITPEM&ME的概率谐波潮流计算流程图Fig.2 Flow chart of probabilistic harmonic power flow calculation based on ITPEM&ME

3 算例分析

3.1 仿真系统

本文基于IEEE 33 节点系统[23]展开分析，系统的接线图如图3 所示。其中，OLTC 为有载分接开关，PV 为16 节点接入风机电源，W 为30 节点接入光伏电源。

图3 IEEE33系统节点接线图Fig.3 Node connection for IEEE 33 system

风机模型采用正态分布，光伏模型采用Beta 分布。当风机与光伏之间相互独立时，分别在节点16与节点30 接入风机与光伏，并作为谐波源节点，本文以谐波源产生的5 次谐波和7 次谐波为例，谐波电流含有率分别取自文献[24]和文献[25]，各次谐波的谐波含有率如表1 所示。

表1 各次谐波含有率Table 1 Each harmonic ratio

3.2 算例分析

3.2.1 统计特征比较

计及风速波动对接入风机出力影响较大，为证明本文所提方法的准确性与可行性，通过4 种工况对概率谐波潮流进行分析计算。

1）工况1：5 次谐波，风速7 m/s。

2）工况2：5 次谐波，风速13.5 m/s。

3）工况3：7 次谐波，风速7 m/s。

4）工况4：7 次谐波，风速13.5 m/s。

以10 000 次MC 模拟得到的概率谐波电压结果作为参考，将期望值及标准差的误差指标作为算法准确度的评价指标，对所求得的概率谐波潮流的精确性进行分析。

定义期望的相对误差如式（8）所示：

式中：μMC为由MC 得到的Z的期望值；μPEM为不同点估计法得到的Z的期望值。

定义标准差的相对误差如式（9）所示：

式中：σMC为由MC 得到的Z的标准差；σPEM为由不同点估计法得到的Z的标准差。

2 种算法计算得到的相对误差结果如表2 所示。

表2 2种算法的谐波电压统计特征相对误差Table 2 Relative error of statistical characteristics for harmonic voltages with two algorithms /%

从表2 中可以看出，2 种算法在求解风光两谐波源节点的谐波电压时，ITPEM&ME 法的相对误差更小。2 种方法在期望值的相对误差上差异性并不大，均未超过0.000 1%，在标准差方面，ITPEM&ME算法在16 节点所求得的相对误差在4 种工况下分别比PEM&GC 法低0.016 4%，0.016 4%，0.016 6%和0.016 3%，在30 节点所求得的相对误差在4 种工况下分别比PEM&GC 法低0.036 6%，0.034 1%，0.037 4%和0.035 8%，最高相对误差达到了近0.04%。这是因为标准差是通过1 阶、2 阶原点矩计算得到的，在估计点采样时，ITPEM&ME 更加完善了采样点的尾部特征，而PEM&GC 忽略了这一点，导致随机变量的各阶原点矩因误差累积逐渐增大。因此，在处理输入变量不确定的问题时，本文提出的ITPEM&ME 算法使用少量采样点即可得到精确的输出谐波电压，有效提高了传统模型的效率，相比于其他方法优势明显。

表3—表6 为不同变异系数约束下4 种工况在采用2 种不同算法时计算得到的谐波电压的相对误差。其中，表示PEM&GC 的期望相对误差，表示ITPEM&ME 的期望相对误差，表示PEM&GC的标准差相对误差，表示ITPEM&ME 的标准差相对误差。

表3 工况1下2种算法的谐波电压相对误差Table 3 Relative error of harmonic voltages with two algorithms under condition 1 %

表4 工况2下不同算法的谐波电压相对误差Table 4 Relative error of harmonic voltages with two algorithms under condition 2 %

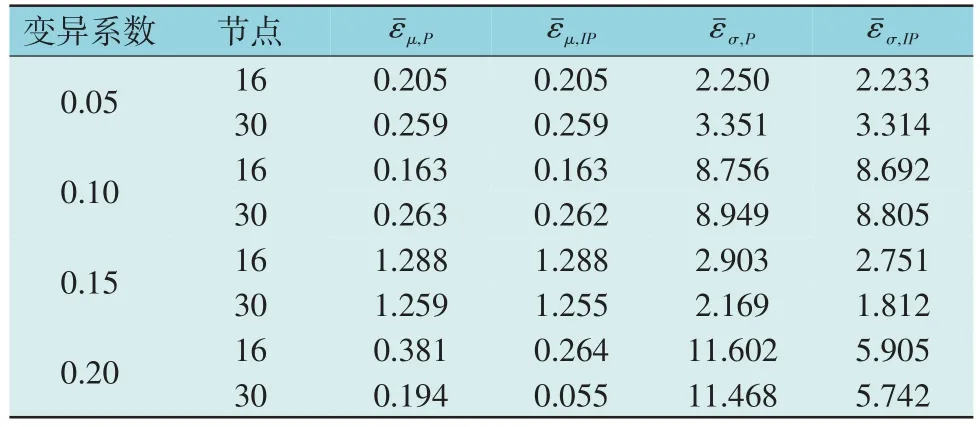
表5 工况3下不同算法的谐波电压相对误差Table 5 Relative error of harmonic voltages with two algorithms under condition 3 %

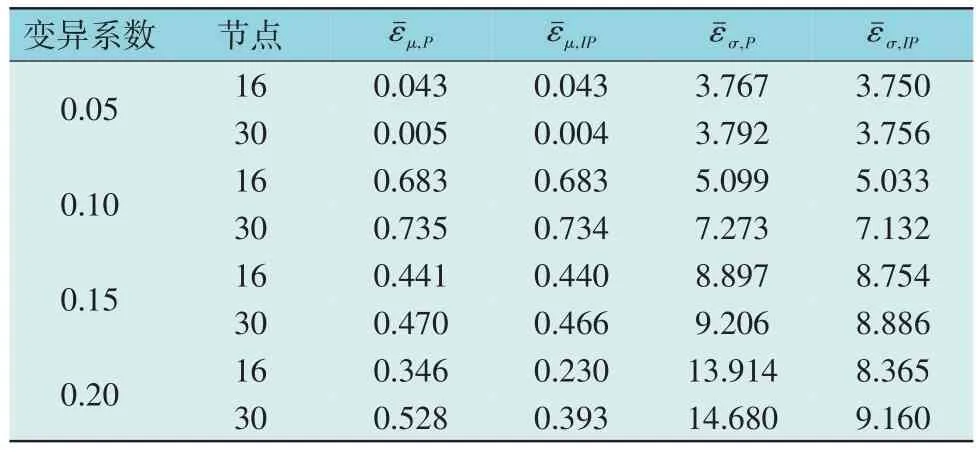
表6 工况4下不同算法的谐波电压相对误差Table 6 Relative error of harmonic voltages with two algorithms under condition 4 %

从表3—表6 可以看出，变异系数的增大导致风-光-荷之间的不确定性增强，因此算法之间求得统计特征的误差也随着不确定性的增大而增大。当变异系数为0.20 时，IPEM&ME 相较于PEM&GC的相对误差更小。因此，IPEM&ME 在不同风速及不同次谐波下的谐波电压的统计特征仍具有较高的精度，说明本文所提出的ITPEM&ME 方法准确性更高，有效提高了传统模型的效率。

3.2.2 分布特征比较

在4 种工况下，针对ITPEM&ME 与PEM&GC和 MC 在概率密度函数（Probability Density Function，PDF）重构上的不同进行对比分析，结果如图4—图7 所示。

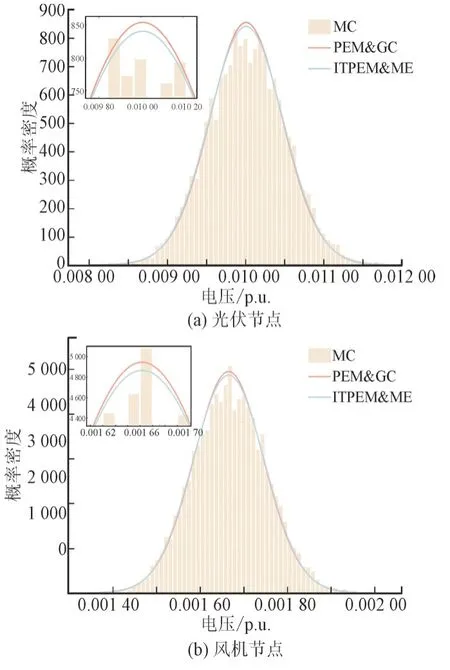
图4 工况1下谐波源节点的PDFFig.4 PDF for photovoltaic and wind turbine nodes under condition 1

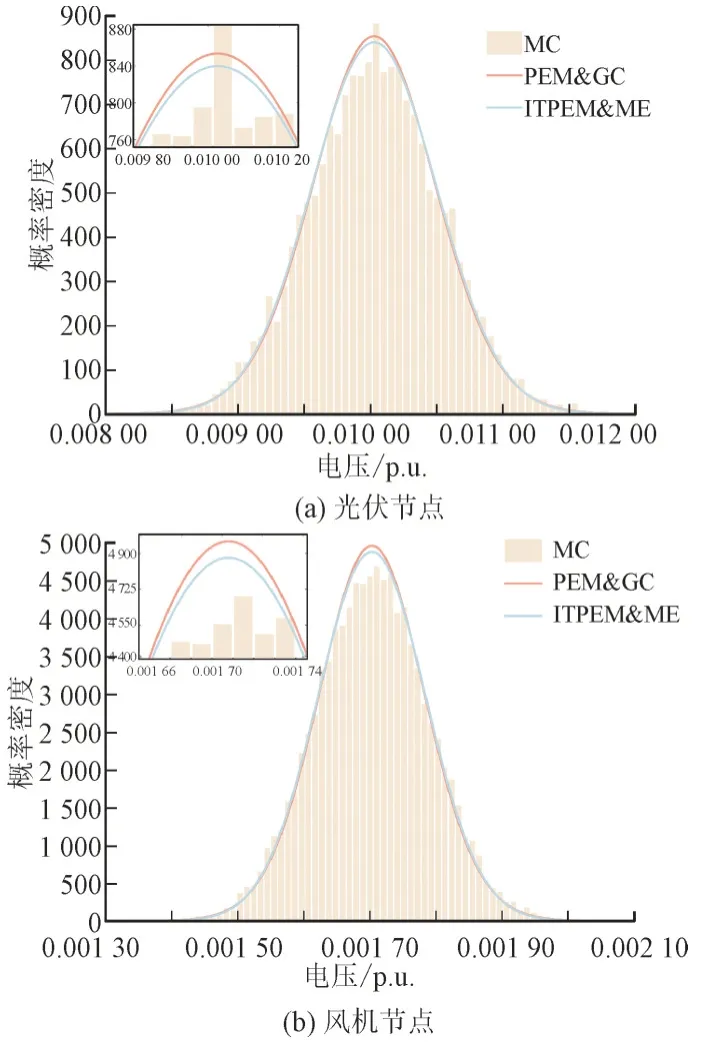
图5 工况2下谐波源节点的PDFFig.5 PDF for photovoltaic and wind turbine nodes under condition 2

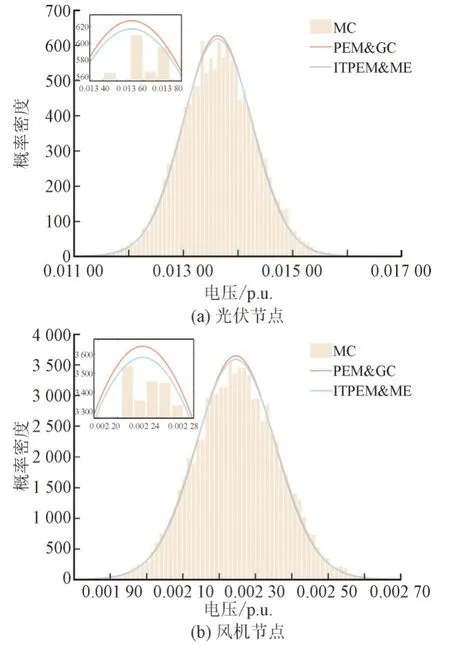
图6 工况3下谐波源节点的PDFFig.6 PDF for photovoltaic and wind turbine nodes under condition 3

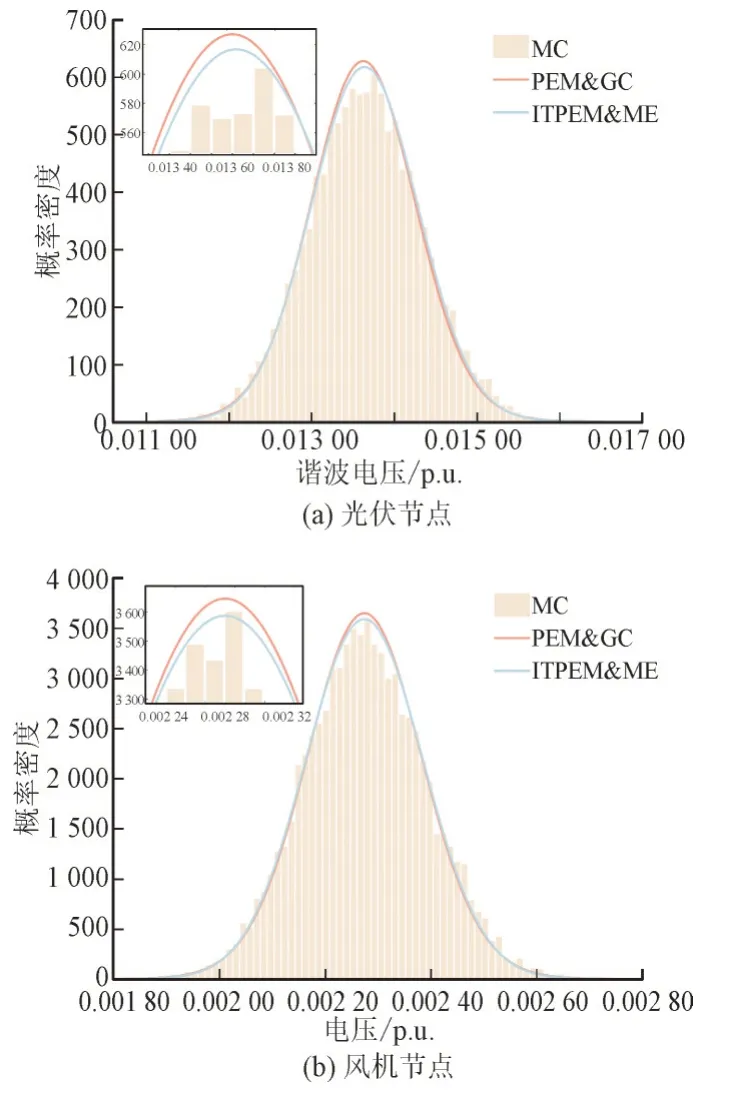
图7 工况4下谐波源节点的PDFFig.7 PDF for photovoltaic and wind turbine nodes under condition 4

由图4—图6 可以看出，本文提出的ITPEM&ME方法相比于传统的PEM&GC 方法在4 种不同工况下的概率密度估计曲线均最贴近MC 模拟出的真实情况。这是因为当系统接入风机后，由于风速的波动性极强，风机节点的出力一般具有较高的高阶累积量，导致在概率密度拟合时最大熵理论只以输入的谐波电压的前4 阶原点矩作为约束条件，通过拉格朗日乘数法求出概率密度函数，而PEM&GC 求出谐波电压的前7 阶原点矩和半不变量对级数进行展开拟合，因此累积造成误差。由此证明了利用统计数据得出的各阶统计矩作为约束条件来近似得出待求随机变量的概率密度函数更为合理，也进一步验证了所提ITPEM&ME 方法在具备高度精确性的同时也可有效地保证概率密度估计的准确性。

4 结论

本文针对配电网中存在风机、光伏及负荷的出力不确定问题，提出了ITPEM&ME 方法，从统计特征求取以及概率密度函数拟合两方面对其进行改进，实现了对谐波电压及其统计特征高效求解的效果，既保证了计算精度，又提高了计算效率。具体结论如下：

1）考虑到风-光-荷的随机性与波动性对配电网造成的影响，提出改进三点估计模型解决谐波潮流问题。所提算法计算效率更高，能够对随机性输入变量作出更精确近似。

2）通过最大熵理论对求得的谐波电压分布进行精确拟合，简化计算的同时提高了精度，且求得的概率密度函数更接近实际情况。

3）所提算法准确度较高，统计得到的谐波电压的期望和方差等统计特征均优于PEM&GC 方法，因此可更精确地处理配电网中存在的风-光-荷不确定性问题。

在对谐波电压的统计信息进行估计时，忽略了风机和光伏之间存在的相关性造成误差，故在下一步的研究中应添加风机与光伏的相关性，进一步分析其对谐波潮流的影响。