基于有效降低解空间和优选典型场景的配电网随机机会综合优化

2023-07-17刘明红刘自发贾政豪廖孟柯

智慧电力 2023年6期

李清，刘明红，王威，刘威，刘自发，贾政豪，廖孟柯

（1.国网新疆电力经济技术研究院，新疆乌鲁木齐 830002；2.山东科技大学智能装备学院，山东泰安 271019；3.华北电力大学电气与电子工程学院，北京 102206）

0 引言

配电网络重构[1-2]是一个大规模的0-1 规划问题，当考虑其它的控制设备，例如电容器[3-4]和软开关（Soft Open Point，SOP）[5-7]，转化为综合优化问题，是一个大规模的混合整数非线性规划（Mixed Integer Nonlinear Programming，MINLP），如何高效、准确的求解是配电网优化面临的一个难题。

配电网综合优化求解方法可分为两类，一是交替求解法，二是同时求解法。尽管交替求解法[8]降低了问题的规模，但从一个解到另外一个解很容易陷入局部最优解。为此，同时求解法得到了广泛的研究，该方法分为启发式方法和解析法，启发式方法[9-11]虽然易于实现，但只能理论上获得最优解，且对于大规模的配电网综合优化，计算效率偏低；为了高效获得更精确的解，解析法被广泛深入的研究，文献[12-14]通过忽略线损、电压平方项近似等于电压幅值等方法，将非线性的潮流方程线性化，且为每条支路引入2 个二进制决策变量来满足辐射状约束，将该问题转化为一个混合整数二阶锥规划求解，虽然线性化的潮流方程降低了求解难度，但影响求解精度。为此，在非线性潮流方程基础上，文献[15]利用大M 法和二阶锥松弛将优化模型转化为混合整数二阶锥规划。文献[16]提出基于弦松弛的混合整数半定规划模型，虽然二阶锥松弛技术相对于线性化的潮流方程提高了求解精度，但对辐射状约束仍需每个开关引入2 个二进制决策变量，仍是一个大规模优化问题。文献[17]利用模拟退火法实现开关状态的快速求解，在已知开关状态的基础上，采用锥优化方求解配电网运行时序优化问题，虽然有效避开大规模二进制决策变量的引入，但模拟退火法属于启发式方法，影响解的精度。

当配电网接入可再生能源（Renewable Energy Sources，RESs）后，配电网综合优化就转化为不确定性优化问题，考虑到鲁棒优化的保守性，采用随机机会约束规划求解，但综合优化的随机变量较多，且为非线性方程，不能转化为等价的确定形式[18]，采用随机模拟的方法求解，如何高效获得典型场景是随机模拟法研究的关键问题。文献[19]根据随机变量的概率分布每次产生随机变量，在完成给定次数随机模拟后，判断是否满足机会约束条件，但场景过多，会降低计算效率，而且每个方案都需要重复计算过程，计算效率低。为此，文献[20]先将期望场景加入典型场景集合并求解，然后将主要的违反约束的场景每次加入1 个到典型场景集合并求解，重复此过程，直到满足机会约束为止，相对文献[19]提高了计算效率，但每次选择违反约束的场景增加了解的保守性，文献[21]首先给出满足机会约束的最少场景数，然后随机选择场景构成典型场景集合，虽然能够满足机会约束条件，但随机选择场景也会导致解的保守性。

随机性的配电网综合优化有2 个关键问题需处理：一是如何避免引入大量的二进制变量，进而高效、准确求解；二是如何确定满足机会约束的场景，避免解的保守性。为此，本文通过优选典型场景，运用基尔霍夫电压和电流定律，近似线性化地逐环优化，实现配电网随机机会综合优化的高效、准确求解。

1 数学模型

1.1 目标函数

节点1 为根节点，根节点电压V1为常数，给定场景集合Ωsce中每个场景s的概率πs，则以损耗Ploss最小为目标的线性目标函数为：

式中：Ωbra为支路的集合；为场景s的首节点或末节点编号为1，另一个节点编导为j的支路电流的实部；ΩRES为分布式可再生能源RES 的集合；PRES,s,m为第m个RES 在场景s的有功功率；Ωld为负荷的集合；Pld,n为第n个负荷的有功功率。

1.2 基尔霍夫定律

电网络一定满足基尔霍夫电压定律和电流定律：

1.3 SOP的优化模型

SOP 以背靠背电压源型变流器（Back to Back Voltage Source Converter，B2B VSC）[5]为例，控制模式为PQ-VdcQ，对应的潮流计算节点类型为PQ-PQ节点，运行约束如下：

式中：PSOP,s,i和QSOP,s,i分别为场景s下节点i的SOP注入的有功功率和无功功率；PSOP,s,j和QSOP,s,j分别为场景s下节点j的SOP 注入的有功功率和无功功率；ΔPSOP,s,i和ΔPSOP,s,j分别为场景s下接在节点i和j上换流器的损耗；ASOP,s,i和ASOP,s,j分别为场景s下接在节点i和j上换流器的损耗系数；SSOP,s,i和SSOP,s,j分别为场景s下接在节点i和j上换流器的容量。当JSOP,s,i被PSOP,s,i和QSOP,s,i替换，方程如下：式中：为场景s下连接SOP 的节点i电压。

1.4 开关状态优化模型

当所有的开关都闭合后，形成一个少环网，假定每一个基本回路串联一个电压源，优化计算得到串联电压源矢量Es，则可根据式（10）计算优化后的基本回路电流Iloop：

式中：Y为l×l阶回路导纳矩阵。

然而，实际的配电网没有串联的电压源，为此，提出如图1 所示的等值变换方法，通过断开少环网开关近似获得优化后的基本回路电流，图1 中nloop为环网计数器的数值。

图1 开关状态优化的等值变换方法Fig.1 Equivalent transform method for optimization of switch status

图1 的过程相当于配电网重构，将大规模的0-1 整数规划问题转化为小规模的连续变量优化，决策变量为连续的基本回路电流，同时基本回路数远小于开关数。

1.5 可再生能源、电容器和负荷优化模型

式（3）的JRES,s,Jld由RES 的功率替换：

式中：PRES,s,i和QRES,s,i为场景s下节点i的可再生能源有功功率和无功功率；为场景s下节点i电压幅值。

式（3）的Jld由负荷的功率替换：式中：Pld,i和Qld,i为场景s下节点i的负荷有功无功功率。

式（3）的JCB,s由电容器投切组数替换：

式中：ni为节点i上电容器投入组数；bi为节点i上电容器的单组电纳。

1.6 限值及机会约束

电容器投入组数满足如下约束：

式中：为电容器组最大投入组数。

节点电压和支路电源的机会约束方程如下：

另外，配电网还需满足辐射状约束。

2 求解方法

2.1 基于典型场景的算法整体流程

对于Ωsce中的场景，采用场景树[22-23]方法缩减后的场景，用集合Ωred,sce表示，在Ωred,sce中首先选择概率最大的场景放入典型场景集合Ωtyp,sce，然后每次选择与典型场景集合中心欧式距离近的场景加入典型场景集合，基于每次构成的典型场景集合获取优化方案，然后利用所有场景Ωsce判断优化方案是否满足式（15）和式（16）的机会约束规划，直到获得目标函数式（1）的最小值。图2 给出算法总体流程，其中ns为典型场景综合Ωtyp,sce的场景数，Ploss,k为第k个场景下的损耗。

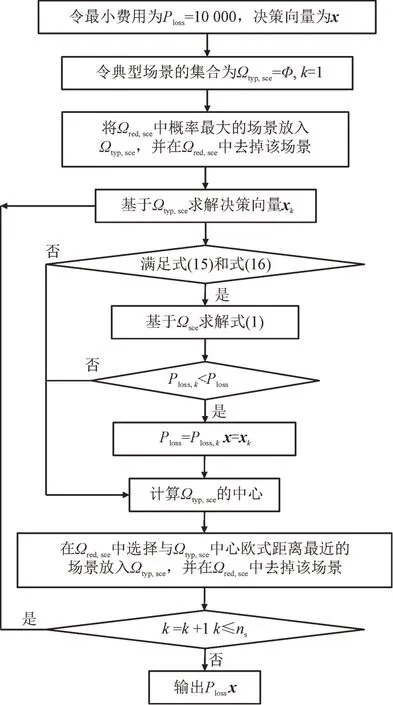
图2 基于典型场景的算法总体流程图Fig.2 Overall flowchart of proposed algorithm based on typical scenarios

图2 算法每次选择与典型场景集合中心欧式距离近的场景加入到典型场景集合，而不是像文献[20]选择违反约束的场景或文献[21]随机选择场景加入典型场景集合，避免了解的保守性。

2.2 基于二阶锥松弛、近似线性化的逐环打开求解方法

在利用典型场景Ωtyp,sce求解决策变量的条件下，式（1）修改为：

利用所有场景Ωsce求解机会约束方程，式（15）和式（16）修改为：

然而，式（4）—式（13）是非线性方程，影响了求解的精度，为此本文采用二阶锥松弛、近似线性化的方法求解。

式（4）—式（8）可采用旋转二阶锥松弛[12]：

若忽略线损，假定各节点电压为额定值Vn，式（11）—式（13）近似线性化为：

式（2）、式（3）、式（10）—式（13）和式（17）—式（26）构成一个二阶锥规划，可高效求得决策变量Iloop，PSOP,s,i，QSOP,s,i和ni，利用1.4 小节的等值变换方法每次决策1 个断开开关，注意支路电流也取各场景的均值，直到获得辐射网。结合1.4 小节重构转化为小规模连续变量优化问题，在计算规模大幅度减少的前提下，再结合文献[24]的扩展序分量法，可以应用到多相混合配电网的优化，增加了算法的适用范围。

3 算例仿真及分析

本文采用IEEE 33 节点[25]和IEEE 69[26]节点系统为例，利用CPLEX12.7 编程求解。

3.1 算例数据

IEEE 33 节点和IEEE 69 节点如图3 和图4 所示，包括增加的电容器组、RES 和SOP，其中，1，2，…，69 表示节点，1，2，…，69 表示支路。节点1电压的标幺值为1，限值是[0.9，1.07]，置信水平1-ε是0.95，假定所有RES 的有功功率服从高斯分布，均值是1 755 kW，方差是175 kW，电容器组的单组容量是50 kvar，组数是24，SOP 的容量是385 kVA，损耗系数是0.2，无功功率限值范围是[-240，240]kvar。

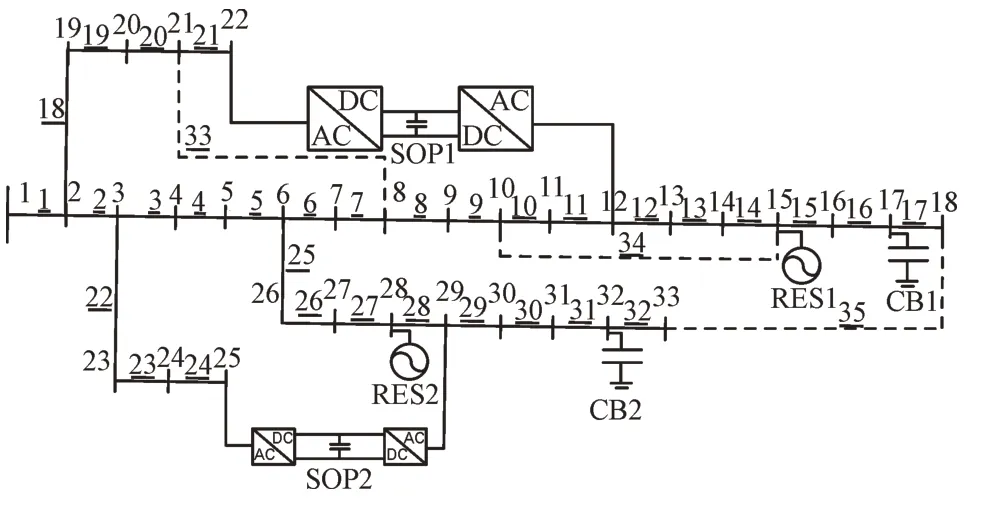
图3 修改后的IEEE33节点系统图Fig.3 Modified IEEE 33-bus system diagram

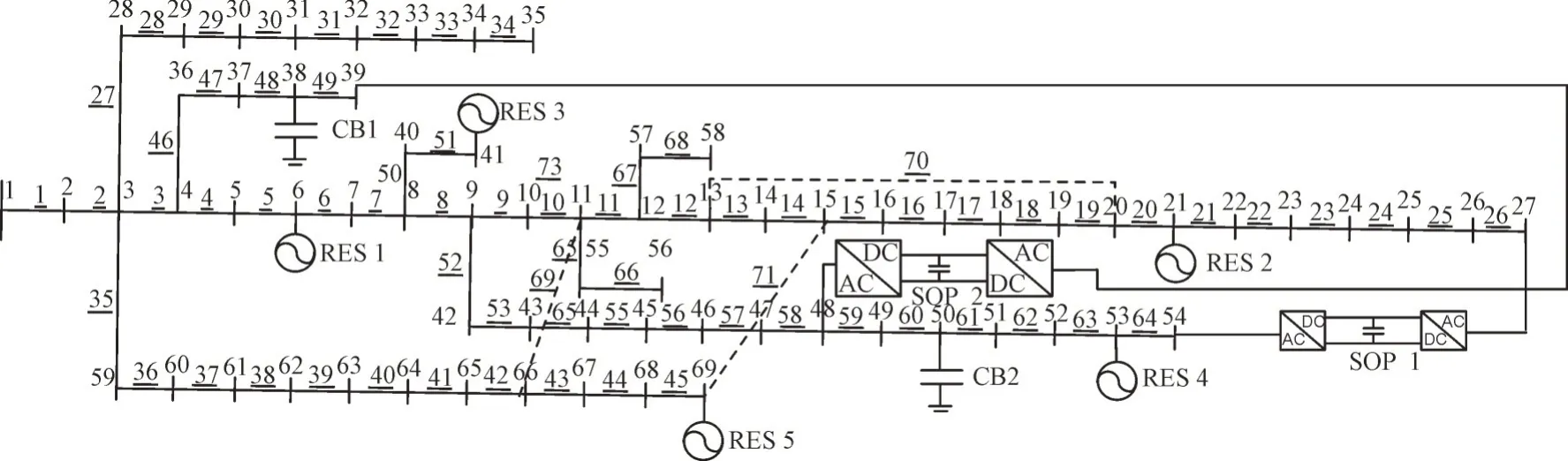
图4 修改后的IEEE69节点系统图Fig.4 Modified IEEE 69-bus system diagram

3.2 相同求解方法条件下不同场景构建方法仿真及分析

为了证明提出的典型场景集合生成方法的优越性，表1 给出了在不同的典型场景集合生成方法条件下，采用2.2 节提出的相同求解方法的线损优化结果。

表1 不同典型场景集合生成方法的线损优化结果Table 1 Results of line loss optimization with different typical scenario set generation algorithms kW

如表1 所示，就IEEE33 节点和IEEE69 节点系统，本文方法的线损分别是60.29 kW 和218.85 kW，小于文献[20]集合生成方法的优越性。原因是在本文方法中，可再生能源出力在区间[1351.35 kW，2158.65 kW]范围外的值没有加入到典型场景中，而文献[20]和[21]有部分值加入到典型场景中，尽管数量不多，但依旧影响优化结果。

3.3 相同的典型场景集合条件下不同求解方法仿真及分析

在相同的典型场景集合条件下，采用文献[10]的粒子群算法和文献[15]的解析法分别求解，优化后的线损如表2 所示。

表2 相同典型场景集合条件下不同优化方法的线损Table 2 Results of line loss optimization with different algorithms under same typical scenario set condition kW

如表2 所示，就IEEE 33 节点和IEEE 69 节点系统，本文方法计算的线损分别是60.29 kW 和218.80 kW 最小，与文献[10]的粒子群算法60.31 kW和218.82 kW 接近，明显小于文献[15]的解析法的61.32 kW 和219.03 kW，证明了本文算法的准确性。为了进一步证明提出算法的高效性，表3 给出了粒子群和解析法的优化时间。

表3 相同典型场景集合条件下不同优化方法的计算时间Table 3 Computing time of different algorithms under same typical scenario set condition s

如表示3 所示，本文方法的计算时间分别是14.53 s 和14.81 s，小于解析法的61.2 s 和77.11 s，更小于粒子群算法的509.96 s 和608.23 s。这是因为本文方法大规模缩小了解空间，本文算法优化决策的是基本回路电压，而粒子群算法和解析法优化决策的是开关的状态变量。本文方法的决策变量个数分别是10 和10，包括2 个基本回路电压、2 个电容器组数和6 个SOP 决策变量，粒子群算法优化决策的变量个数分别是40 和38，包括32 个开关状态变量、2 个电容器组数和6 个SOP 决策变量，解析法优化决策的变量个数分别是101 和104，包括32 个开关状态变量、64 个辅助二进制决策变量、2 个电容器组数和6 个SOP 决策变量。