某新能源汽车翼子板结构性能优化分析

黄李冰 吴文军

摘 要：为满足轻量化技术要求，翼子板作为遮盖车轮的覆盖件通常会设计成较薄的部件，其结构性能直接影响整车的性能品质，因此需要对翼子板的结构性能进行优化分析。文中搭建了某新能源汽车翼子板有限元模型，根据相关设计要求分别对翼子板进行模态分析、连接刚度计算和抗凹性分析，依据计算结果寻找出不满足目标值要求的指标。经综合分析，提出以增加内支撑板的方式来改进翼子板的结构，从而解决翼子板的刚度以及抗凹性不足的问题，但一阶固有频率无法满足目标值要求。因此，通过响应面法搭建克里金近似模型，以结构改进后的翼子板的质量和一阶固有频率为目标进行遗传算法迭代寻优，使得改进后的翼子板的整体质量稍有下降，一阶固有频率大于53.00 Hz，且其余各项指标均符合目标值要求，达到优化目的。

关键词：翼子板；有限元模型；响应面法；多目标优化；遗传算法

中图分类号：U469.720.3 DOI：10.16375/j.cnki.cn45-1395/t.2023.03.001

0 引言

汽车翼子板为遮盖车轮的外壳板，其刚度的强弱直接影响整车的刚度。为减轻汽车质量，通常将汽车翼子板设计成较薄的部件。因汽车翼子板结构特征较少、厚度较薄，导致其在进行作业时会发生偏软或出现永久变形、刚度不足等问题[1]。翼子板在刚度不足的情况下进行大载荷作业，会因自身结构遭到破坏而导致周边部件的振幅增大甚至会产生共振现象[2]。另外，翼子板是一个双曲度扁壳的车身覆盖件，其屈曲抗凹性不足会导致变形以及行驶中产生噪音等影响车身品质的问题[3-5]。因此，在汽车研发初期对汽车翼子板进行模态、刚度、抗凹性等结构性能分析必不可少。如今国内外学者对汽车翼子板的研究也积累了一定的学术成果和工程经验。例如，文献[6]通过对带充电口的翼子板进行工艺优化以改善尺寸精度；文献[7]为了获得翼子板成型的最佳工艺参数，对可调变量进行实验优化以获得影响翼子板成型质量的工艺参数的最优组合；文献[8]针对某乘用车前翼板进行模具设计及成型工艺参数优化。若按照传统方法、凭借经验，通过频繁调整工艺参数以达到开发设计翼子板的目的，不仅耗时耗力且不符合市场竞争需求。有限元仿真技术的快速发展，解决了生产中出现的实验条件苛刻和实验成本高等技术难题[9-10]。

结合工程实际需要，文中对某型号新能源车翼子板的模态、连接刚度、抗凹性进行分析，发现存在不符合目标值要求的性能指标。依据工程经验进行综合分析，通过增加内支撑板对翼子板结构进行改进。改进后的翼子板的刚度、抗凹性的各项性能指标均得到改善，但一阶固有频率却稍有下降。因此，采用响应面法搭建克里金近似模型，以结构改进后的翼子板的质量和一阶固有频率为目标进行遗传算法寻优以达到优化目的。

1 翼子板结构有限元仿真分析

1.1 翼子板的模态分析及刚度分析

文中选用某新能源汽车翼子板结构为分析对象，其板厚为1 mm，材料为B180H1冷轧板，弹性模量为210 GPa，泊松比为0.3，材料密度为7.85 g/cm3。为了保证计算结果的准确度，需要对翼子板结构进行几何清理，并尽量保留翼子板的原有特征线。采用四边形单元进行网格划分，网格尺寸为8 mm，利用集中质量单元模拟结构中的螺栓连接。鉴于翼子板结构的振动主要是由车身振动引发的，因此需要进行翼子板结构的约束模态分析。图1为翼子板模态及刚度分析设置图。依据结构的实际安装形式，在翼子板与车身安装点的螺栓连接处均施加固定约束，车身安装点位置约束如图1（a）所示。在进行连接刚度仿真分析时，要对翼子板的各安装点位置施加50 N法向载荷，其中安装点位置包括5个外缘点、3个前保连接点、3个大灯连接点，连接点加载如图1（b）所示。

将翼子板模型进行模态和刚度计算，得到固有频率模态振型图和连接点刚度位移变形图。

1）模态计算结果显示，翼子板非约束区域的振幅较大，幅值从自由边处向非约束区域、约束区域逐次递减，如图2所示。翼子板的一阶固有频率为52.08 Hz，并不满足所设定的目标值大于53.00 Hz的要求。

2）从各连接点刚度的计算结果中发现，其余加载点位置剛度均符合要求，除了如图3所示翼子板的第3个大灯连接点，其位移变形量为1.522 mm，即刚度为32.85 N/mm，不满足目标值大于50.00 N/mm的要求。

1.2 翼子板的抗凹性分析与计算

屈曲抗凹是针对外板的刚度和稳定性进行分析，通过对外板可能发生屈曲的部位进行加载，根据分析结果与目标值的对比来评价外板件的屈曲抗凹性能。前期的抗凹性试验由于存在较多限制条件，且薄弱点的位置会随着翼子板结构的修改而发生变动，因此，以工程经验判断薄弱点的位置并不可靠。为提高工作效率和准确性，将选取15个加载点（P1～P15）进行加载分析，通过对比的方式进行翼子板的抗凹性分析[11]。在进行翼子板抗凹性分析时，针对15个加载位置，以加载点为中心，分别选取长宽均为50 mm的区域进行网格细化，如图4所示。在周边全约束条件下，分别在选取的15个点的垂直面上放置厚度为1 mm、半径为20 mm的小球撞击块，在其垂直方向上线性施加50、150和400 N的载荷。

如图5所示，翼子板不满足抗凹性的情况如下：在初始载荷为50 N时，P2点的抗凹刚度值为29.39 N/mm，小于目标值30.00 N/mm；在施加载荷到400 N时，P4、P8、P9分别在325、350、210 N附近出现油壶效应。油壶效应[12]是评估抗凹稳定性的一个指标。在施加载荷过程中，冲击载荷超过某临界值时，抗凹刚度突然严重下降就会产生油壶效应。实际工程中为避免车身覆盖件产生油壶效应，一般采用增加板厚、调整安装位置、增加支撑板等方法，并通过不断试验找出最合理的结构形式，尽量减少油壶效应的影响。

2 结构改进措施分析

通过对翼子板的模态、安装点位置的连接刚度与屈曲抗凹性分析发现，其一阶固有频率不达标、大灯连接点3刚度低和抗凹性不足。结构改进方案有：更改产品的材料类型；增加产品的材料厚度；增加支撑板；改变外覆盖件结构。对于外覆盖件，增加材料厚度可以提高刚度，但不满足轻量化的要求，也不符合经济性；外覆盖件对造型设计有严格要求，对其进行结构优化设计时要求尽量不影响其外板面造型等。经过综合分析，为满足模态、刚度和抗凹性要求，采用增加内支撑板的方式可达到改善翼子板性能指标不足的目的[13]。

针对上述对翼子板的分析结果，通过在翼子板内部增加支撑板来提升翼子板的各项性能。翼子板支撑支架设计为“Y”字形，由3块板组成，并通过焊点与翼子板内部翻边形成焊接关系，通过模拟粘胶的方式，将翼子板与支撑板连接，既能保证翼子板的支撑性，又不会影响外板面造型，如图6所示。根据企业工程经验设置内支撑板T1、T2、T3的厚度分别为1.0、1.2、0.6 mm，此时翼子板的总质量为5.091 kg。

如图7、图8所示，结构改进后的翼子板的一阶固有频率从52.08 Hz降低至50.78 Hz，未达到优化目的；大灯连接点3处的位移变形量由1.522 mm降低至0.646 mm，刚度从32.85 N/mm提升至77.39 N/mm，满足目标值要求，达到优化设计的效果。由图9结构改进后的翼子板的载荷-位移曲线图可知，施加内支撑板后的翼子板，其P2点抗凹刚度值由29.39 N/mm提升至58.00 N/mm；无油壶效应产生；屈曲抗凹的其余加载点各项指标均满足目标要求。

3 多目标优化分析

3.1 近似模型相关理论

设[y（x）]为目标或者约束的近似函数，克里金模型[14]假设系统的响应值与自变量之间的关系可以表示为：

[y（x）=f（x）+z（x）]. （1）

式中：[f（x）]在统计过程中称为涨落；[z（x）]为稳定随机分布函数，反映了局部偏差的近似。

3.2 试验设计

试验设计（design of experiments，DOE）方法作为响应面模型的采样方法广泛应用于工程和科学研究等领域，是获取数据和分析数据的合理、高效的手段，其主要目的是确定近似模型的样本点数以及其在空间中的分布。计算机模拟测试软件提供了多种DOE方法，不同的方法适用的条件不同。哈默斯雷采样适用于响应面高度非线性的情况，能够用较少的样本点提供可靠的结果统计量估计，是目前在基于有限元单元法的DOE方法中最有效的采样措施。结构改进后的翼子板的連接刚度和抗凹性的各项指标达到研究目的，但是一阶固有频率尚未达到目标值要求，因此，需要作进一步优化。拟选择哈默斯雷算法对内有支撑板的翼子板进行空间填充，为响应面拟合提供数据。

以翼子板的3块内支撑板厚度[x1]、[x2]、[x3]为设计变量进行样本采集，初始设计变量信息如表1所示。

为了得到精确的近似模型，对选择的3个变量进行哈默斯雷试验设计作为输入矩阵。根据采样数据提取的响应为：结构改进后的翼子板的一阶固有频率、大灯连接点3的刚度以及质量。而克里金近似模型使用采样数据的响应值进行响应面拟合。若采样点不完全落在响应面上则会产生误差，拟合的精度通常由决定系数[R2]来表示，[R2]计算公式为：

[R2=1-i=1n（yi-yi）2i=1n（yi-y）2] . （2）

式中：[yi]表示第[i]个样本点的精确模型响应值，[y]表示在第[i]个点的拟合预测值。

通常认为决定系数[R2]的值越接近于1，表示拟合的效果越好。通过误差计算结果来进行近似模型的精度评价，发现翼子板质量[R2]的值为0.992 9，一阶固有频率[R2]的值为0.986 1，大灯连接点3位移变形量[R2]的值为0.900 9。由此可知，该近似模型具有较高的拟合精度，满足替代实际模型作优化计算的条件。

3.3 寻求最优解

通过克里金近似模型进行计算分析得到设计变量与响应量之间的映射关系。设定响应量为优化目标函数，通过多目标[15]遗传算法对该优化问题进行求解。其中，约束函数限定变化范围，缩小了寻优范围，提高了寻优率。

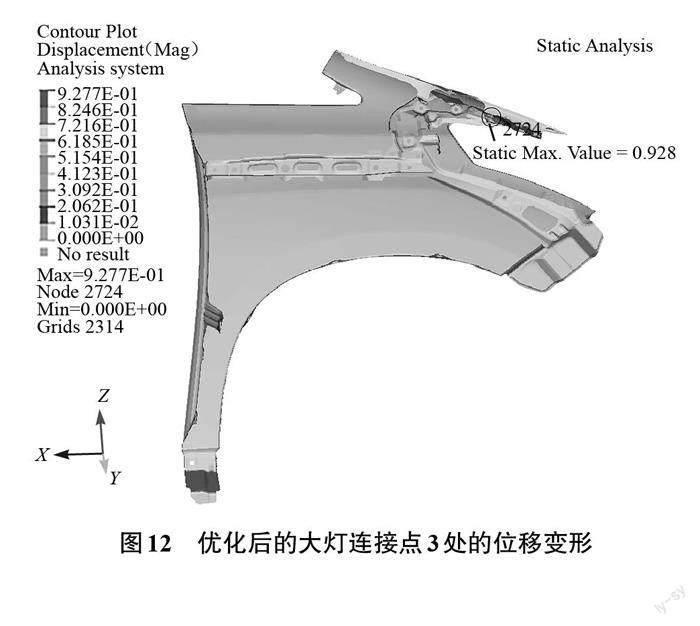
在翼子板优化过程中，以其质量及一阶固有频率为优化目标，以大灯连接点3的位移变形量为约束，取值范围为（0，1）（单位：mm）。经过50次的多目标遗传种群迭代、3 080次计算，得到质量与频率的帕累托最优解集，如图10所示。而帕累托最优解是一个复杂的解集，需要根据实际要求进行筛选。基于轻量化技术要求以及提高一阶固有频率的同时，翼子板的其他结构性能指标均需在目标值范围内才符合此次寻优的目的。因此，根据迭代结果选择其中最优解的一组，其设计变量值为[0.84，1.38，0.46]，取圆整后为[0.8，1.4，0.5]，所对应的质量为5.078 kg。将优化得到的数据代入模型进行修改，重新提交求解器进行计算，得到图11和图12。此时，一阶固有频率为53.75 Hz、大灯连接点3的位移变形量为0.928 mm，保证了翼子板的其他结构性能指标均在目标范围内，符合研究目的。

4 结论

文中通过有限元数值模拟仿真技术对翼子板模态、刚度、抗凹性进行分析，对翼子板局部刚度缺陷以及抗凹性不足的区域进行优化分析并提出改善方案。针对局部刚度不足区域以及为改善翼子板的抗凹性，采用增加支撑板的方式来解决，改进后的翼子板抗凹性能以及连接刚度各项指标均满足目标值要求，但是一阶固有频率尚未达到目标值要求。因此，为进一步达到优化目的，对结构改进后的翼子板搭建克里金近似模型，以一阶固有频率和质量为优化目标，通过多目标遗传算法寻优。优化后得到一阶固有频率为53.75 Hz，大于目标值53.00 Hz。结构改进后翼子板的质量从5.091 kg降至5.078 kg，大灯连接点3的位移变形量为0.928 mm，其刚度值为53.94 N/mm，大于50.00 N/mm，仍在目标值研究范围内，达到优化目的，且其余性能指标均在研究范围内。

参考文献

[1] 吴萌，李能文，杨苑君，等. 汽车塑料翼子板的应用及可行性分析[J].纤维复合材料，2019，36（2）：49-53.

[2] 黄伟，常尊辉，杜雪周. 基于行人保护的汽车翼子板设计和优化[C]//第十五届中国CAE工程分析技术年会论文集，2019：293-297.

[3] 苏亚辉，李亚鹏. 汽车翼子板抗凹刚度有限元分析[J].内燃机与配件，2021（22）：60-61.

[4] TAO W，LIU Z，ZHU P，et al.Multi-scale design of three dimensional woven composite automobile fender using modified particle swarm optimization algorithm[J].Composite Structures，2017，181：73-83.

[5] 李正华，刘小青，方方. 某SUV车型翼子板抗凹性分析和优化[J].内燃机与配件，2018（22）：20-21.

[6] 程岩. 带充电口的翼子板工艺优化研究[J].锻造与冲压，2020（4）：24-27.

[7] WU P，WANG Y M，WAN P.Study on simulation of stamping process and optimization of process parameters of fender[J].Advances in Materials Science and Engineering，2019，2019（1）：1-9.

[8] LUO W B，TANG L F，GUO F C.Mold design and forming process parameters optimization for passenger vehicle front wing plate[J].Journal of Mechanical Science and Technology，2022，36（1）：187-196.

[9] 王兴，吴明明，王江龙. 基于有限元法和田口方法的翼子板成形工艺参数优化[J].河南工学院学报，2020，28（6）：13-18.

[10] 肖红波，蔡浩华. 汽车前翼子板冲压成形工艺优化[J].锻压技术，2016，41（2）：35-38.

[11] 付逸群，张顺，刘峰. 一种提升翼子板抗凹性的优化结构[J].汽车与配件，2017（20）：80-81.

[12] LEE S，QUAGLIATO L，PARK D，et al.A buckling instability prediction model for the reliable design of sheet metal panels based on an artificial intelligent self-learning algorithm[J].Metals，2021，11（10）：1533-1534.

[13] 宋凯，王超，陈涛，等. 基于可变工况的车身覆盖件抗凹性全流程优化方法[J].机械科学与技术，2015，34（4）：599-602.

[14] 于向军，张利辉，李春然，等. 克里金模型及其在全局优化设计中的应用[J].中国工程机械学报，2006（3）：259-261.

[15] 方晓耿，谌炎辉，谢国进. 模块划分的多目标评价方法研究[J].广西科技大学学报，2017，28（4）：119-123.

Structural performance optimization analysis

of a new energy vehicle wing plate

HUANG Libing， WU Wenjun*

（School of Mechanical and Automotive Engineering， Guangxi University of Science

and Technology， Liuzhou 545616， China）

Abstract： Wing plates are usually designed as thinner parts to cover wheels， and their structural performance affects the performance quality of the vehicle， so it is necessary to optimize the structural performance of the wing plates. In this paper， a finite element model of a new energy vehicle wing plate is built. According to the relevant design requirements， the modal analysis， connection stiffness calculation and anti-concave analysis of the wing plate are carried out respectively. According to the calculation results， the indices that do not meet the requirements of the target value are found. Through comprehensive analysis， it is proposed to improve the structure of the wing plate by increasing the inner support plate. The problem of insufficient stiffness and dent resistance of the wing plate is solved， but the first-order natural frequency cannot meet the target value. Therefore， the Kriging approximation model is built by the response surface method， and the genetic algorithm iterative optimization is carried out with the quality and first-order natural frequency of the improved wing plate as the target. The result shows that the overall quality of the improved wing plate is slightly reduced; the first-order natural frequency is greater than 53.00 Hz; and the remaining indices meet the target value requirements. This achieves the optimization purpose.

Key words： wing plate; finite element model; response surface method; multi-objective optimization; genetic algorithm

（責任编辑：黎 娅）