基于RBF神经网络的双色LOGO塑件成型工艺优化
2023-07-15张君黄瑶周甫芝王雷刚
张君 黄瑶 周甫芝 王雷刚*
(1.江苏大学材料科学与工程学院,江苏 镇江,212013;2.丹阳凯新精密模具有限公司,江苏 镇江,212132)
随着人们对汽车外观美感要求的提高,越来越多的双色注塑件被应用于汽车外饰系统和灯光系统。这类塑件加工后容易出现气泡、缩痕、翘曲变形等质量问题[1-3]。
大量学者就如何消除注塑缺陷做了相关研究:杨建强等[4]利用计算机辅助工程(CAE)软件和多目标参数优化方法得到了非均匀壁厚塑料制件的最佳质量;张鲁滨等[5]以某塑料叶轮为研究对象,建立了基于反向传播(BP)神经网络的注塑件翘曲预测模型,并采用平均影响值(MIV)算法将模型预测的相对误差由13%降至7%;雷继梅等[6]以高光三色汽车尾灯灯罩为研究对象,基于不完全因子试验设计建立了塑件翘曲量与工艺参数之间的响应模型,运用此模型进行注塑工艺参数优化,试生产后得到了变形量小、质量较好的产品;Kumar D 等[7]采用遗传算法优化注塑工艺参数,提高了产品的质量。
下面以某汽车贯穿灯LOGO 塑件为研究对象,先通过正交试验和CAE 软件模拟仿真得到模拟结果,再基于径向基函数(RBF)神经网络建立了塑件质量指标与注塑工艺参数之间的函数关系模型,得到了最优参数组合,提高了产品质量。
1 模流分析方案建立
1.1 塑件结构及材料分析
贯穿灯LOGO 塑件如图1所示。外形尺寸为256 mm×66 mm×64 mm。原料为聚碳酸酯(PC),前面白色部分为第一射,属于厚壁件;后面灰白色部分属于第二射。第一射部分壁厚较大且不均,注塑过程中容易产生气泡、缩痕等缺陷。灰白色部分含有较多卡扣,用于将塑件固定在贯穿灯内装饰框上,要求较高的装配精度。
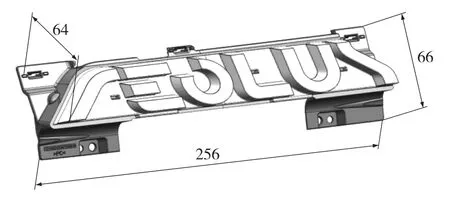
图1 贯穿灯LOGO 塑件示意(单位:mm)
1.2 初步模拟
先将三维模型与浇注系统导入CADdoctor软件中进行修复,修掉细小圆角,提升网格质量;再将修复好的模型导入Moldflow 软件中划分3D 网格,分析类型为重叠注塑,分析程序选择“填充+保压+第二部分填充+第二部分保压+翘曲”,划分网格后定义浇口位置;最后根据系统推荐工艺进行注塑模拟,得到的翘曲值(W)为1.857 mm,缩痕指数(S)为8.260%。
2 正交试验设计
2.1 成型工艺选择及试验
设计正交试验的因素和水平需要根据产品的结构、材料的属性和研究目标来确定。第一射塑件是厚壁件,容易产生缩松缩孔等缺陷;二射是薄壁件,容易产生翘曲缺陷,且装配精度要求高。因此,以第一射塑件的S和W为优化目标。对塑件质量影响较大的因素如下:第一射的熔体温度(A/℃)、保压压力(B/MPa)、保压时间(C/s);第二射的熔体温度(D/℃)、保压压力(E/MPa)、保压时间(F/s)。根据初步模拟时软件推荐的工艺参数,确定其水平范围,然后采用CAE 软件进行模拟。正交试验因素及水平如表1所示,正交试验如表2所示。
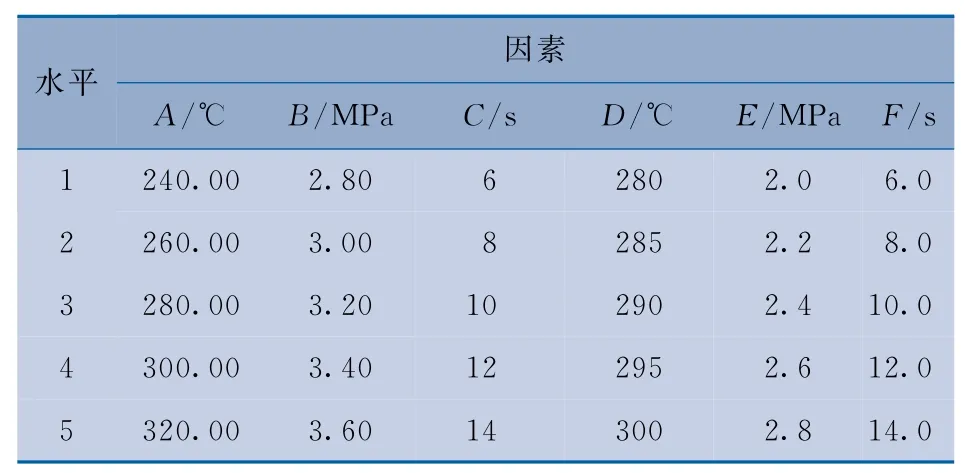
表1 正交试验因素及水平
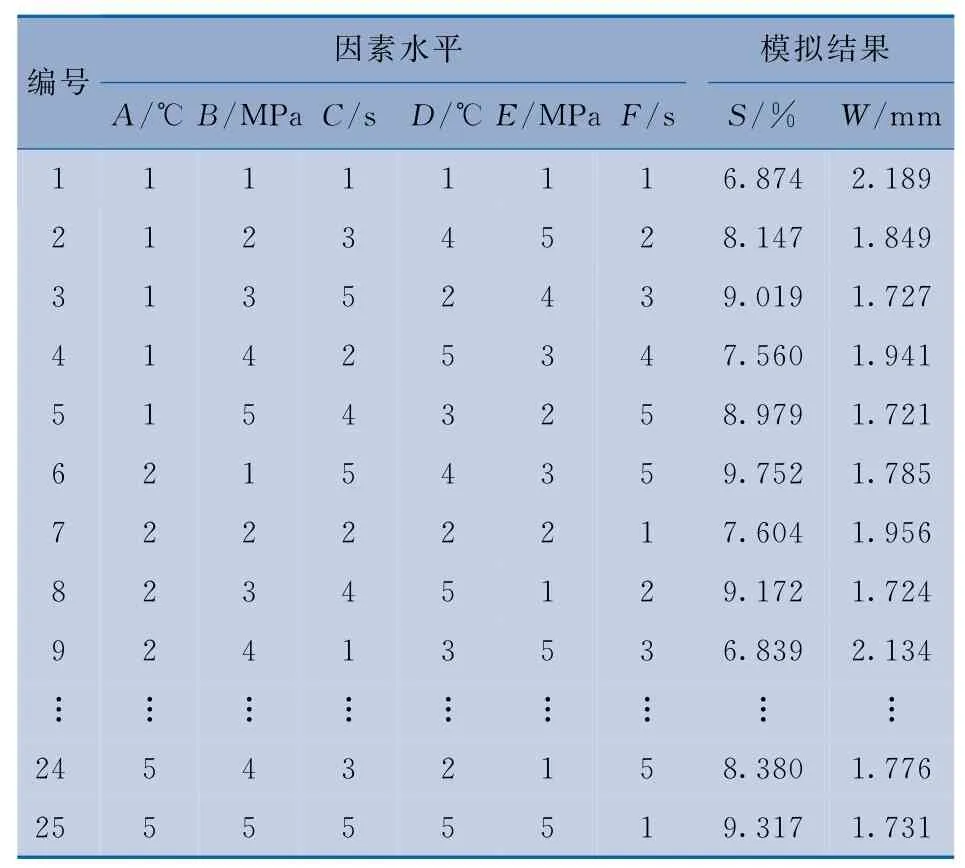
表2 正交试验
2.2 试验结果分析
表3和表4分别为S及W在各因素水平上的均值。
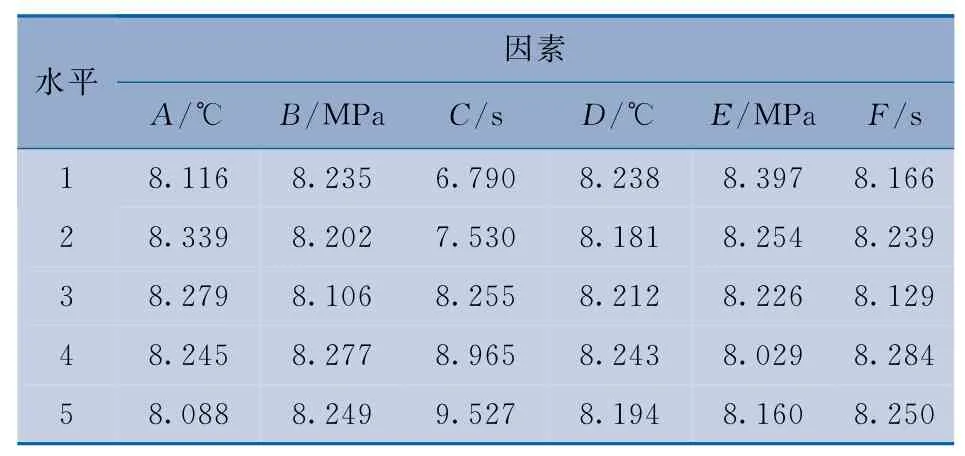
表3 S 均值%
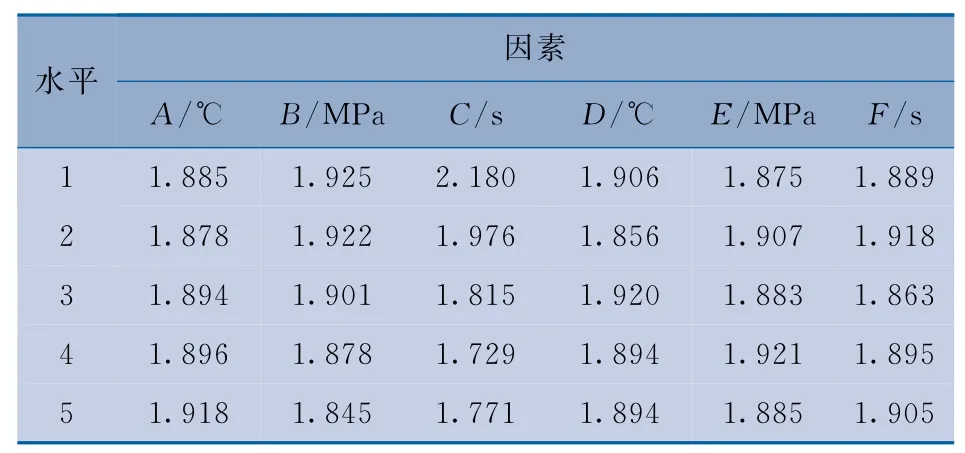
表4 W 均值mm
由表3和表4可以看出:获得最小S的最佳工艺参数组合是A5B3C1D2E4F3,获得最小W的最佳参数组合是A2B5C4D2E1F3,两者的最优参数组合不同。为了同时获得较小的S和W,需要进行多目标参数优化。
3 模型建立
3.1 建立RBF神经网络模型
优化目标和注塑工艺参数之间为非线性关系,可以用RBF神经网络建立3层神经网络,将非线性问题转变为线性问题,其结构如图2所示,其中,阈值Φ0恒等于1,假设神经网络输入层为M维,隐含层为N维,输出层为J维。具体过程如下:先随机选择训练样本(xk)作为基函数的中心,求解出所选中心之间距离的最大值(dmax);再将样本向量输入隐含层节点中,计算样本向量与基函数中心的距离,将该距离值带入径向基函数(通常为高斯型函数)解算后得到隐含层的输出(Φi);最后将各隐含层的输出与相应的权值(wij)相乘,进行线性组合,得到最终的输出层(ykJ)[8]。
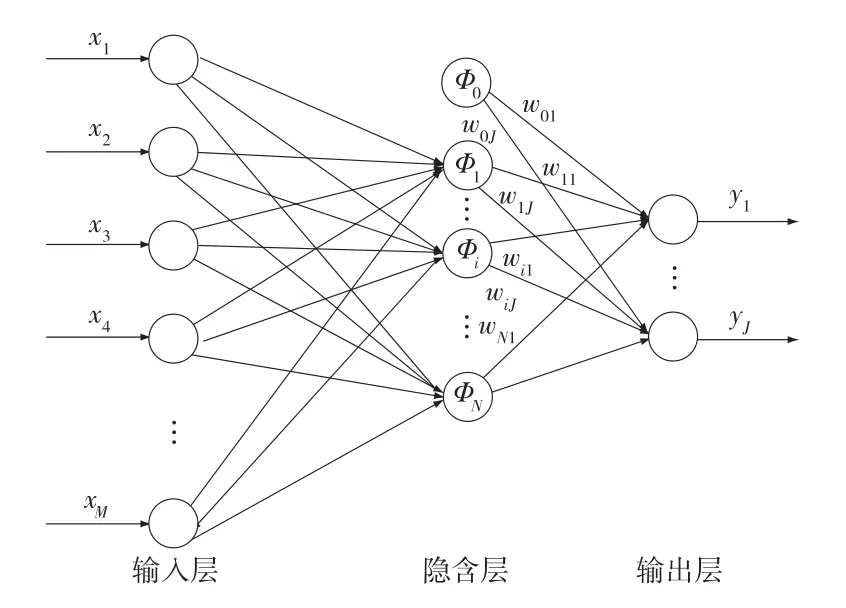
图2 广义径向基神经网络结构示意
3.2 RBF神经网络的训练与检验
以第5,10,15,20,25组工艺参数组合为测试样本,其余20 组工艺参数组合为训练样本。在MATLAB中调用newrb 函数建立RBF 神经网络,均方根误差设置为1.0×10-5,扩散速率设置为100,最大神经元个数设置为25,用训练样本数据训练出神经网络模型,训练完毕后,用挑出的5组数据对神经网络模型进行可靠性测试,结果如表5所示。
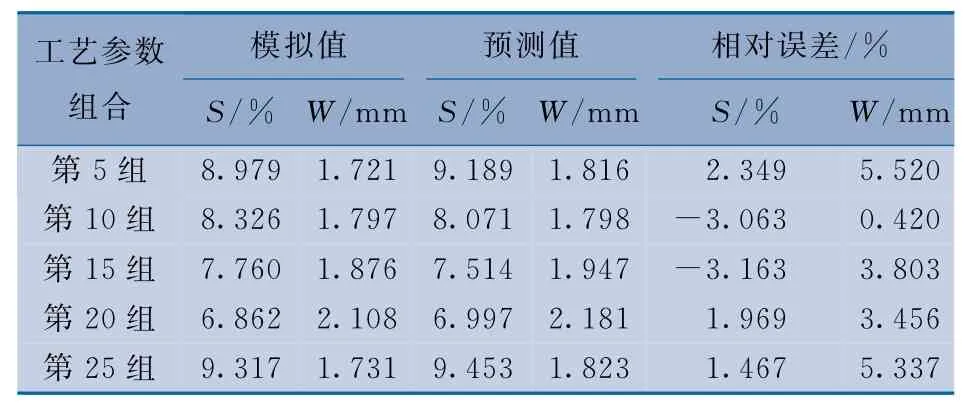
表5 测试结果
由表5可以看出,预测值与模拟值非常贴近,相对误差均小于6.000%。
RBF神经网络模型精确度的评价指标还包括均方根误差(RMSE)和决定系数(R2),计算公式如下所示:
式(1)和式(2)中:n为试验次数;¯y为模拟平均值;xi为预测值;yi为模拟值。
当RMSE越接近0、R2越接近1时,RBF神经网络模型越精确。经计算可得:RMSE(S)=0.203 0,R2(S)=0.956 4;RMSE(W)=0.077 4,
R2(W)=0.945 5。表明建立的RBF 神经网络模型非常精确。
4 参数优化与生产验证
寻优算法采用非支配排序遗传算法(NSGA),过程如下:首先在设定的参数范围内随机生成数组工艺参数作为父代种群,然后将其带入函数模型,得到相应的2个目标值,比较每组工艺参数目标值之间的大小,得出每组工艺参数之间的支配关系,再根据支配关系将每组工艺参数分配到相应的序列,计算每层序列中目标值的拥挤度,之后随机选择序列小且对应目标值拥挤度大的工艺参数进行交叉变异操作,得到子代工艺参数,再计算子代工艺参数对应的目标值,然后将父、子代工艺参数合并得到新种群,再对新种群进行非支配排序和拥挤度计算,最后选择序列小、对应目标值拥挤度大的工艺参数作为新父代进入下一个循环,直至最大循环次数终止循环。
将径向基神经网络模型集成到Isight软件的优化模块中,设定好工艺参数的上下限,每代种群的个数设置为12个,总共迭代20代,寻优后的结果如图3所示。
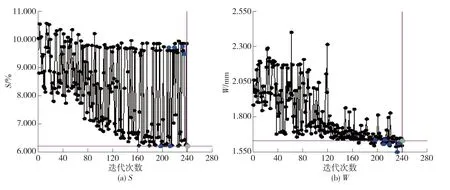
图3 寻优结果
由图3可以看出:迭代至最后一个工艺参数时取得最优值,对应工艺参数为:A为288.30℃,B为3.58 MPa,C为6 s,D为300 ℃,E为2.8 MPa,F为12.9 s,S为6.215%,W为1.631 mm。
将该组优化参数在Moldflow 软件中进行模拟分析,模拟结果如图4 所示,可得:S为6.122%,W为1.643 mm,可以看出模拟值与预测值偏差较小,数据吻合度较高。
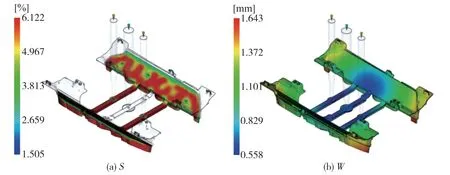
图4 模拟结果
将优化后的工艺参数应用于实际生产,得到的产品如图5所示。从图5可以看出,产品表面光滑,无气泡和缩痕等缺陷,S和W均满足要求。

图5 产品示意
5 结论
设计了正交试验,根据得到的试验样本构建了RBF 神经网络模型,基于该模型得到的遗传算法优化结果和模流分析结果基本吻合。对优化结果进行生产验证,所得产品能够与贯穿灯其他组件无阻碍装配,表明基于正交试验设计与RBF 神经网络模型的双色厚壁塑件工艺参数优化方法切实有效。
