对粗糙集上的不完全信息非合作博弈的均衡分析①
2023-07-15毛浪杨彦龙
毛浪, 杨彦龙
贵州大学 数学与统计学院,贵阳 550025
博弈论又被称为对策论, 是研究决策者在决策过程中所选择的策略形成的不同局势以及策略的均衡.在经典的博弈论理论中, 将博弈分为不完全信息博弈和完全信息博弈.不完全信息博弈是指在不充分了解其他参与人的特征、策略空间以及收益函数的情况下的博弈.
1965年, Zadeh发表的《模糊集理论》[1]为之后的模糊数学研究提供了系统的理论基础.现如今模糊集理论已经应用到不动点理论、变分不等式和博弈论等许多领域[2-4].
1982年, 波兰数学家Pawlak创立了粗糙集理论[5], 作为刻画不完整性和不确定性的数学工具, 能有效地分析不精确、不一致、不完整等各种不完备的信息, 还可以对数据进行分析和推理, 从中发现隐含的知识, 揭示潜在的规律.因此, 粗糙集理论被广泛使用在机器学习、数据挖掘、图像处理、模式识别等许多领域.国内外针对模糊不完全信息的单独博弈大都基于模糊集理论[6-9].目前利用粗糙集理论来解决博弈论中不确定性问题的研究相对较少[10-14].文献[14]在文献[11]的基础上进一步分析不完全信息博弈的粗糙均衡并讨论了不完全信息古诺博弈的粗糙均衡.本文在以上研究的基础上给出了不完全信息博弈的粗糙均衡的存在性定理并对n人古诺博弈的粗糙均衡进行了讨论.
1 预备知识
设U是论域,R是一等价关系, 则(U,R)称为近似空间.设X是U的子集,x∈X⊂U, 则[x]R表示根据等价关系R构成的不可分辨元素的集合, 为R-元素集, 所有等价类集合记为ind(R).用U中所有具有属性R的元素的集合来表达X时, 则有的元素一定属于X, 而有的元素不一定属于X.当给定近似空间(U,R), 对于每一个子集X和一个等价关系R, 可根据R的基本集合的描述来划分集合X, 从而得出下近似和上近似的定义.
定义1[5]设X⊂U,R是一个等价关系, 那么当X可以由ind(R)中的集合的并表示时, 则X是R可定义的, 否则,X是R不可定义的.
定义2[5]若集合R-(X)={x|x∈U,[x]R⊂X}, 则称R-(X)是X(X⊂U)的R-下近似集.
定义3[5]若R-(X)={x|x∈U,[x]R∩X≠∅}, 则称集合R-(X)是X(X⊂U)的R-上近似集.
定义4[5]令R-(X)={x|x∈U,[x]R⊂X}为下近似集,R-(X)={x|x∈U,[x]R∩X≠∅}为上近似集.如果R-(X)=R-(X), 则称X关于近似空间(U,R)是可定义的, 否则称X关于近似空间(U,R)是粗糙的, 简称为粗糙集.
下近似表示根据等价分类R判断一些元素(具有不可分辨性)组成的集合一定属于X, 即[x]R中的元素根据等价分类R一定属于X.上近似表示通过R, 一些元素组成的集合与X的交集非空, 即根据R其中有的元素可能属于X, 有的元素可能不属于X.上近似集和下近似集之差被称为X的R-边界集, 记为BNR(X)=R-(X)-R-(X).由于存在边界区域, 集合中的某些元素既不能在全域的某个子集上被分类, 也不能在它的补集上被分类, 这就产生了不确定性.集合的边界区域越大, 则精确度越低.




2 模型和Nash均衡的存在
下面先给出文献[17]中经典的n人静态贝叶斯博弈模型.记-i=N{i}为除了局中人i以外其他n-1个局中人.
古诺双寡头竞争经济模型是不完全信息博弈的一个经典例子.在古诺双寡头竞争经济模型中, 假设企业不知道其它企业是低成本还是高成本的, 但是假定一个企业知道其他企业类型的概率分布.为了更贴近现实情况, 假设Pi是不容易得到的, 因此, 在这种情况下, 贝叶斯博弈模型不再是合适的分析工具.粗糙集理论是建立在分类机制的基础上的, 它将分类理解为在特定空间上的等价关系, 而等价关系构成了对该空间的划分.基于粗糙集对于信息的分类作用并根据已知信息便能够推断出局中人类型(或是属性)上的近似精确度.例如可以从公司的财务报表知道成本、盈利等信息, 并根据这些信息推断出这个公司是成本低还是高)和是否是盈利型的.建立博弈模型如下:
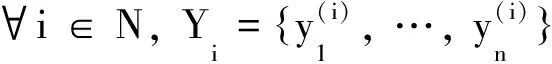
定义6若存在策略组合x*∈X满足
则称x*是博弈G的一个粗糙Nash均衡,

定理5设G={X1, …,Xn;Θ1, …,Θn;d1, …,dn;u1, …,un;Y1, …,Yn}是一个满足以下条件的粗糙非合作博弈: 设∀i∈N
(i)Xi是局部凸Hausdorff拓扑线性空间中的非空凸紧集,


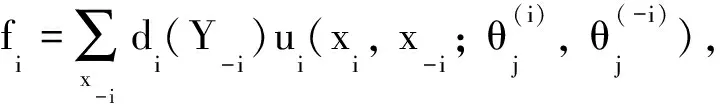
则G有一个Nash均衡.

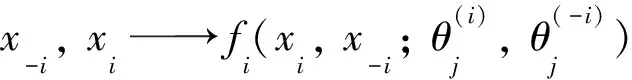
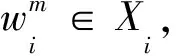
推论1当di(Y-i)=1时, 定理5与Nash均衡定理4是等价的, 此时为完全信息静态博弈.
3 算例
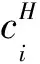

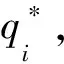
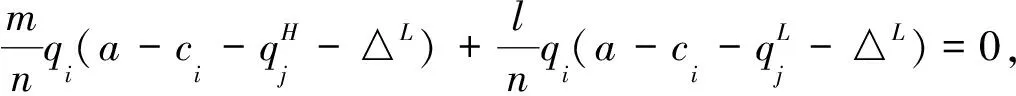
当企业i是低成本时有
当企业i是高成本时有
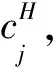
当企业j是高成本时有
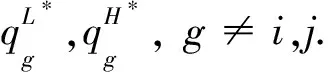
值得注意的是, 本文中仅讨论了固定其他n-2个企业都是低成本的情况, 当然也可以假设其他n-2个企业的类型不相同或都为高成本, 这正好符合现实经济的复杂性和变动性.
4 结论
本文研究了基于粗糙集上的不完全信息非合作博弈.证明了粗糙Nash均衡的存在定理.模型(B)是对模型(A)的一种扩展, 极大地保留了原始信息的客观性, 具有更强的实用性和理论价值.本文仅研究了模型(B)的均衡解存在性问题, 对于其均衡解的稳定性研究将是下一步的工作.
