基于深度残差回归网络和图像块预置信度的盲图像质量评价研究①

齐博， 张国华， 于立子

东北石油大学秦皇岛校区 大数据与计算机科学系，河北 秦皇岛 066004

信息传输技术的发展使图像这一信息载体形式得到较大范围的应用, 且数据网络连接密切程度的增加也使社交手段中图像信息的应用频率提高.图像信息使用方式在社交生活、安全防范以及交通运输等领域均具有较好的、积极的作用, 能有效且直观地传达出信息的表现内容.图像信息质量越高, 则其在传输过程中的信息损失较小, 但在图像的采集编码和传输交换等过程中, 不可避免地会存在因图像信息失真而致使图像质量较差的问题[1].而且在不同评价标准下, 图像质量存在一定的差异, 认知体系、环境条件, 以及评估者自身心理活动和偏好等都会使图像在进行主观评价时存在感知差异.盲图像质量评价(blind image quality assessment, BIQA)在比较过程中不存在可参考的高清图像, 其仅从失真图像本身进行评价, 故其精度很难得到较好的保证.胡晋滨等[2]借助Wasser-stein距离生成条件对抗网络以实现失真图像的复原, 并对复原图像进行分块采样和卷积处理.通过借助VGG-19卷积神经网络(convolutional neural network, CNN)池化特征提取、特征灰度处理, 以及图像与特征之间的对应相似性得分计算.该研究提出的方法在场景模拟仿真训练中表现出较好的性能和准确性, 具有较高的主观一致性.陈勇等[3]提出将空间域和变换域应用到盲图像立体评价中以改善立体图像质量预测质量欠佳的问题, 并将提取的合并场景统计特征输入到支持向量机中, 构建特征域上的质量分数预测模型.结果证明该方法在立体图像数据评价上的均方根误差为5.603, 具有较高的有效性.借助深度学习网络进行盲图像质量评价能有效实现对特征信息的提取, 故本研究提出基于卷积神经的残差网络结构, 并基于人眼视觉特点, 设置图像置信区间, 以更好实现对盲图像的质量评价, 以期提高盲图像评价精度, 提高其应用有效性.

1 文献综述

针对当前图文印刷图像存在失真的问题, 陈富伟等[4]提出以元学习方式进行盲图像质量评价, 通过失真先验知识的获取、多层次特征获取以及降维处理及权值融合等操作构建起质量评价模型.该模型在失真测试集上所表现出的SRCC值均在0.85以上, 泛化性能表现较好, 具有较高的图像质量预测分数.面对当前传统高斯降噪算法的低执行效率问题, 徐少平等[5]借助CNN进行图像质量感知的盲图像降噪算法设计, 即以浅层CNN和深层CNN分别实现降噪图像质量的初步估值和给定性评估, 并以分类字典实现不同噪声模式的匹配.结果表明该算法具有较高的降噪效果, 且其在完成效率上表现较好.盲图像视觉评价主要是实现语言描述与数字分数的转换, 但其不可避免地存在相关信息的丢失.心理概念应用到盲图像评价模型中, 能通过对定性评价的直接确定以及质量标签的等级处理来实现数据处理.

针对当前多失真图像质量的评价精度较低的问题, 王同乐等[6]提出以信息损失值作为图像度量值, 借助概率矩阵分解和支持向量回归进行特征向量的构建和模型训练.结果表明该算法与个体的主观评价结果具有较高的一致性.将正常照度图像进行低照度合成以及颜色分量的分解, 陈清江等[7]借助特征提取和双残差卷积获得图像之间的映射关系, 并以双边滤波优化增强图像以使得其趋近于参考图像.实验结果表明该方法下的结构相似度最高趋近于0.95, 盲图像评价指标优于其他对比算法, 有效提高了算法运行效率.张玉波等[8]提出以注意力机制实现图像盲模糊算法的改进, 架构起多尺度循环体系, 并以残差通道选择模块和跨层长连接实现特征提取以避免图像纹理缺失而带来的精度损失情况.其研究结果表明该方法较之经典去模糊网络算法具有较好的应用精度, 其结构相似性有所提升.吴梦凡等[9]从噪声估计、模糊处理和网络重建3个方面进行改进, 并提出降质信息估计的盲图像复原算法, 实现算法的重建处理.其结果表明该算法在主客观质量评价指标上表现较好.冯象初等[10]借助L0范数进行稀疏检验, 并借助博弈理论建立起图像修复模型, 以交替方向乘子法解决算法问题中的最小化问题和收敛性问题, 结果表明该方法在主客观质量评价指标上具有较好的应用性和稳健性.从图像的色彩空间特性出发, 陈扬等[11]提出基于互补色小波变换的图像质量盲评价算法以实现颜色通道信息的把握.并从自然场景图像的设计以及多尺度及方向进行模型构建, 结果表明该评价方法能有效实现失真图像的特征提取, 并具有较高的评价精度.深度学习算法能有效对图像特性信息进行提取, 同时在盲图像评价指标中应注重评价的全面性.其中结构平衡理论考虑了3条边的符号之积来判定其是否处于平衡状态, 将该理论应用到盲图像质量研究中, 就需要在保证其质量精度的同时满足人眼视觉系统, 保证多维度下质量评价结果的平衡.故研究基于深度学习网络, 提出符合视觉系统的图像置信结构, 以期提高图像质量精度.

2 基于深度残差回归网络和图像块预置信度的盲图像质量评价分析

2.1 深度残差回归网络下的盲图像质量评价

盲图像质量评价主要包括特征提取和质量预测两方面, 其主要是通过衡量图像的失真情况以及对模型进行训练以实现图像在客观失真下与主观质量的映射关系.按照其应用场景的差异性, 该质量评价方法包括专用和通用两种方法, 两种方法的区别在于是否对失真的类型进行限定.图像特征与失真特征的相关性较差以及模型的预测性能有限等问题是当前在盲图像质量评价中主要出现的问题[12].为较好实现盲图像质量评价, 本研究引入CNN进行图像特征提取.CNN作为一种深度学习网络, 包含卷积计算以及深度结构, 其作为一种前馈神经网络在图像分类领域有较好的应用效果.同时CNN在训练阶段具有较好的反馈效应和参数调整机制, 故其在进行图像信息特征抽取时能较好地考虑到多维度信息结构, 并在监督学习过程中借助映射实现参数的最优化.CNN的空间不变性使得其在进行特征提取时具有较好的效率, 其结构包括卷积层、激活函数层、池化层以及全连接层.卷积层和激活函数层中的参数多是借助梯度下降法进行优化, 其中卷积层中的卷积核是实现特征信息提取的关键步骤.图像自身具有一定的拓扑结构, 故其形式多借助矩阵进行表达, 参数优化过程就是独立卷积核的特征提取单元经由线性叠加后的最终优化结果[13].同时考虑到卷积层数增多以及网络深度的加深会使得局部特征图的信息存在丢失的情况, 故本研究对卷积操作前的图像进行扩编补零以减少特征图不断缩小的问题.CNN的反向传播主要是在池化层中进行的, 在反向传播过程中, 池化层的残差传播首先需要恢复到预处理前的池化大小.随后判断前向传播策略为均值下采样还是最大下采样来进行池化残差的处理, 即对应将残差值放入平均子矩阵位置还是子矩阵的最大位置.不同卷积层之间的误差递推公式可表达为:

(1)

式中:l,l-1表示卷积层z的当前层及前一层,δl表示当前层l的误差,δl-1为l-1层的误差,w表示卷积层的权重值,b为偏置项,J表示误差矩阵.对卷积核在卷积前进行翻转以及与误差矩阵进行计算, 即可得到上一层的误差.在确定卷积核矩阵元素为wij, 输入值为矩阵大小为4×4的a时, 则可表示出偏置项的梯度, 即:

(2)

借助(2)式, 可对每层神经元的梯度进行推导计算, 并得到相应的卷积层权值和偏置数.同时为减少不同频次特征信息在提取过程中的被稀疏化, 研究在CNN中引入残差网络来避免梯度消失和爆炸问题.残差网络中的残差块结构能在拓宽网络层次的同时降低其层次误差, 图1为残差网络结构.

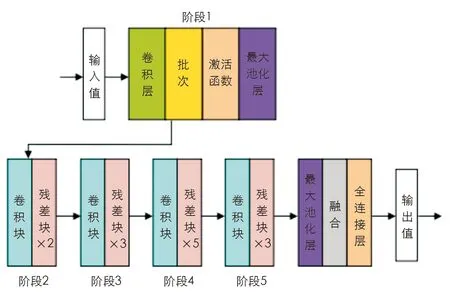
图1 残差网络结构

图1为ResNet50的结构, 输出值在预处理后进入5个阶段的Block结构中, 并将最后运算完成的值输入到全连接层进行分类和归一化处理.当卷积网络层结构越大时, 相应的神经网络具有较高的函数适应性, 但其相应也会使得网络对数据的依赖程度加深进而导致过拟合现象的产生.深度残差网络在进行信息的输入与层级传输时, 会加入恒等映射来避免这种情况.同时残差块结构中的输入与输出之间存在短连接, 其能有效实现映射关系的拟合.残差单元的函数关系可表示为:

(3)

式中:xk表示第k个残差单元的输入,yk为第k个残差单元的输出,F(xk,wk)表示优化目标.每个残差结构之间均存在激活函数h, 令h(xk)=xk,xk+1=yk, 则可以得到反向传播公式为:

(4)

式中:ε表示损失函数,L表示残差单元数.同时考虑到数据库中的图像大小具有不完全一致性, 难以适应全连接层对特征向量维度处理的固定统一性, 故需要在网络设计时将卷积层的特征图进行转化, 保持维数相同.原有卷积网络的原始图像会经由卷积处理和池化操作, 进而得到特征信息图, 且图中被标注的目标区域经过映射处理后可得到映射区.本研究基于感兴趣区的磁化特性, 提出以非均匀步长池化处理来实现特征图的不同移动步长的设置, 即不同大小的输入图像在经由卷积处理后得到的特征图在最大池化过程中具有步长差异[14].应用在盲图像质量评价中的深度残差网络回归模型的学习以差异平均主观分数(difference mean opinion score, DMOS)数据为标记.卷积层中的特征向量为固定维数, 且网络输出值为全连接层的最值节点, 该方法减少了激活函数的映射处理, 可直接得到图像的质量评价分数.

2.2 基于图像预测以及区域置信度的盲图像质量评价

对深度残差网络模型进行优化, 即在原有残差块结构中加入1×1大小的卷积核, 对其进行先降维后升维的操作, 并在输出维度差异下对输入值进行线性映射变换, 减少参数量以提升计算效率.图2为残差块参数改进示意图.

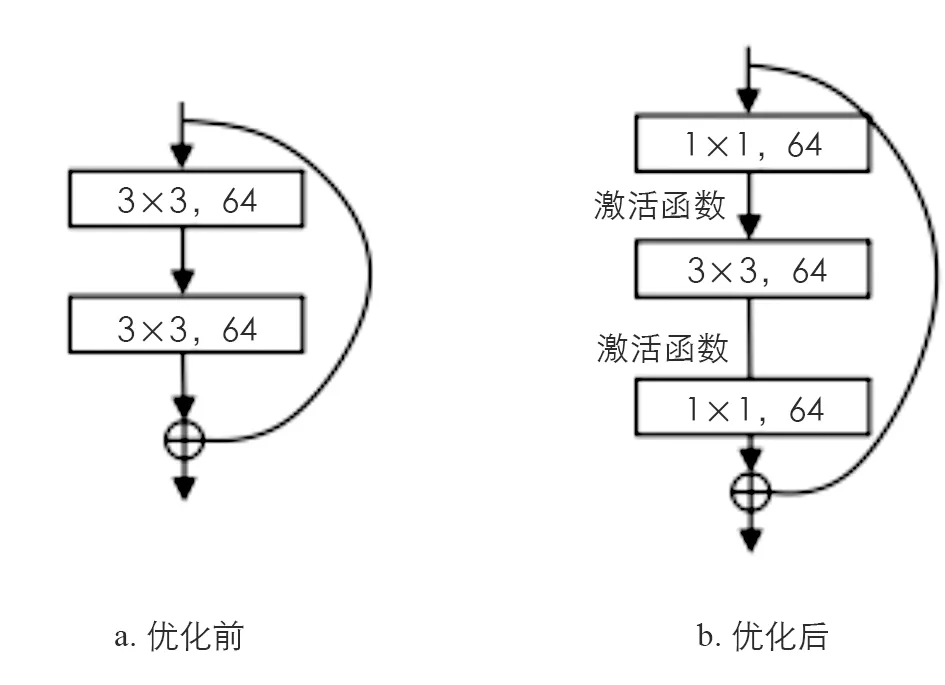
图2 残差块的参数改进

随后研究选择平滑损失函数作为模型构建的损失函数, 其数学表达如式为:

(5)

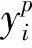
图3 深度残差网络回归模型的示意图

数据库样本量的限制在一定程度上会造成算法网络的过拟合问题, 故本研究设计对图像进行分块处理, 并对不同图像子块的预测分数进行计算及其与图像真实分数之间的拟合程度进行计算.不同图像尺寸划分下预测结果与真实结果之间的一致性存在差异, 亮度对比情况、纹理丰富程度以及背景区域内容和边缘结构信息等指标是比较图像差异的重要内容.图像子块的比较结果与预测值之间可构建起相关置信度模型, 且不同图像子块因预测分数的差异可表现出不同的置信度, 通过对不同子图像块进行预测分析, 就可得到与人眼主观感知系统相一致的结果.同一幅图像中的不同区域目标所包含的信息也有所不同, 图像的均方根误差越大表明其对比度越大, 被感知的程度越明显, 且绝对亮度的差异也能表现不同图像子块之间的区别.故本研究设计基于置信度差异的预测分数加权算法, 以此提高评价的一致性.在置信区间构建过程中, 亮度差异所表现出的图像预测偏差最为明显, 但其数量相对较少, 故本研究以亮度均值的残差来实现不同亮度图像的大小排序, 并得到图像块预测分数的置信区间.

-n*σE≤P≤n*σE

(6)

式中:n表示经验值,σE为残差数据的标准差,E为残差按其绝对值大小进行排序的结果,P表示待评价图像.依据置信区间, 则可得到图像子块的数量、均方根误差和图像子块对应的预测质量分数.

③靳静：《反垄断法价格协同行为的认定研究——以艾司唑仑药品垄断案为例》，载《反垄断法》2016年第9期。

(7)

式中:N为图像子块的数量,C和S为均方根误差和预测质量分数.同时考虑到不同对比度大小划分下的子块预测结果与其真实质量分数之间具有一定的差异, 故本研究借助高斯离散化模型进行置信度计算.通过对不同子块与最大对比度子块之间的距离进行计算, 得到子块所对应的贡献程度, 降低偏差较大的局部区域对预测结果的干扰.高斯拟合函数的数学表达为:

(8)

式中:σ表示置信因子,gi为图像子块的亮度,di为gi与亮度对比最大的图像子块之间的最大距离.置信度在最大距离处趋近于0, 对图像子块的置信度进行归一化处理, 其计算公式为:

(9)

以归一化后的置信度作为图像子块的权重, 即可实现对图像子块分数的预测处理.整体的算法流程见图4.

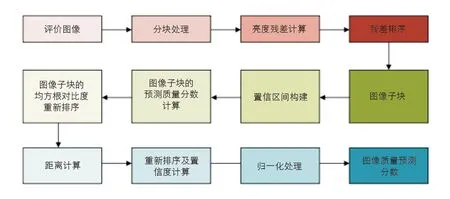
图4 算法流程

在图4中, 对图像子块的筛选需要符合人眼视觉, 且计算各图像子块的均方根误差与最大值之间的距离是进行置信区间重新设计的关键, 以归一化后的置信度作为权重来实现对图像质量的预测, 能有效实现对图像信息特征的提取.

3 盲图像质量评价应用效果分析

在实验过程中, 研究在LiVe图像数据库中选取大型合成失真数据集和真实失真数据集来组成样本实验数据, 并在实验过程中按照6∶4的比例将实验数据划分为测试数据和训练数.其中对训练样本数据进行旋转以及镜像等无损处理以保证样本数据分布的均衡, 并对其进行颜色通道处理, 得到失真图像120幅.其失真类型包括高斯白噪声、空间相关噪声、JPEG压缩以及均值偏移等.裁剪上述图像样本, 得到像素尺寸分别为256,128,64以及32的图像子块.并将裁剪得到的图像子块纳入实验检验中.训练过程中, 统一设置训练批次为16, 初始学习率为0.001, 最大迭代次数为2 000.对本研究对图像进行分块处理后的数据增强效果进行分析, 其结果见图5.

图5 本研究算法改进前后的图像处理结果

从图5可以看出, 在对模型数据进行增强前, 本研究提出的算法在改进后的Pearson 相关系数和Spearman 等级相关系数均值分别为0.937 6和0.951 3, 且数据的损失情况有所改善, 有效避免了数据的过拟合问题, 泛化性能得到了进一步的提高.随后对本研究提出的图像子块预测结果进行分析, 并以统计均值作为预测分数, 其结果见表1.

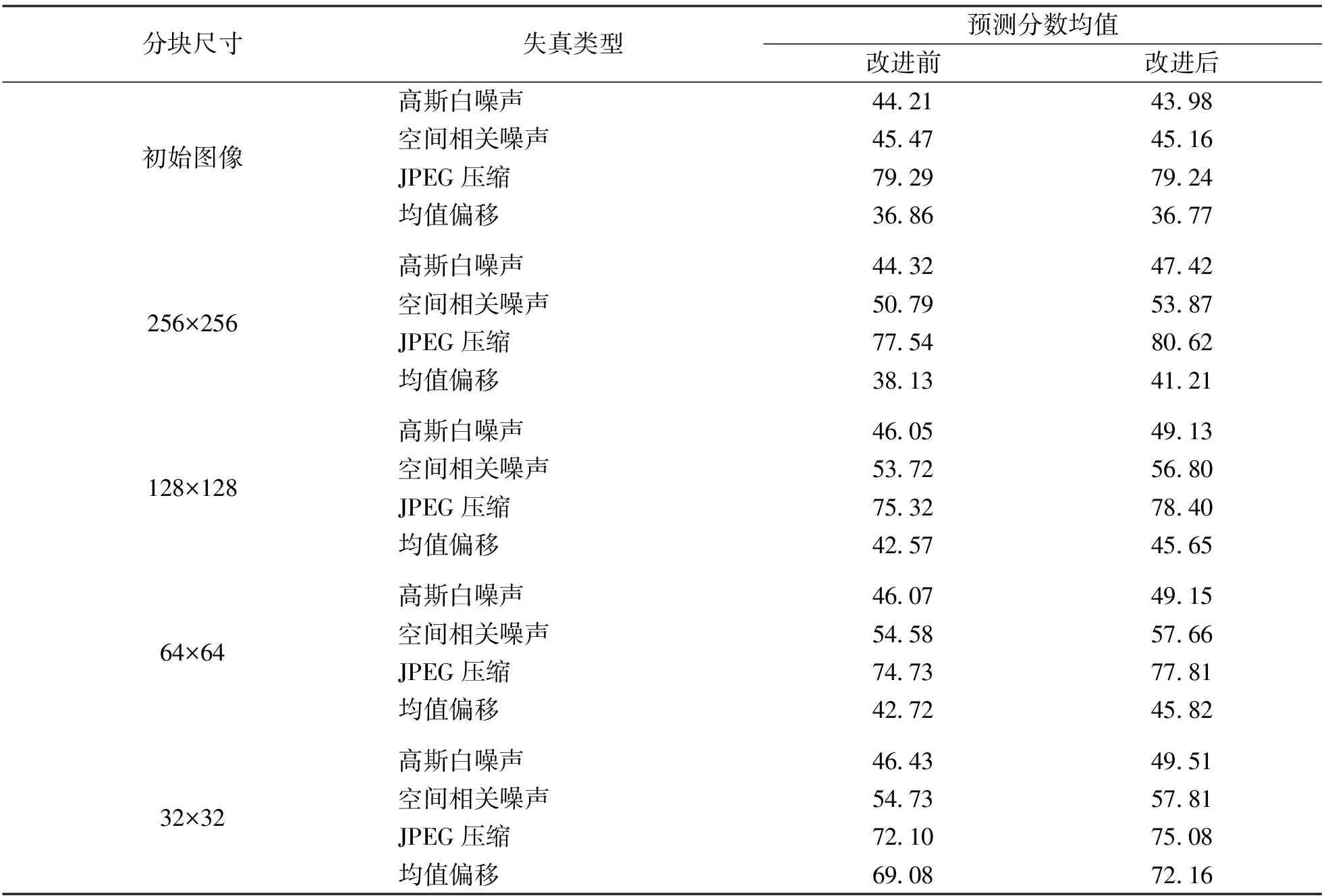
表1 图像子块的预测分数均值结果

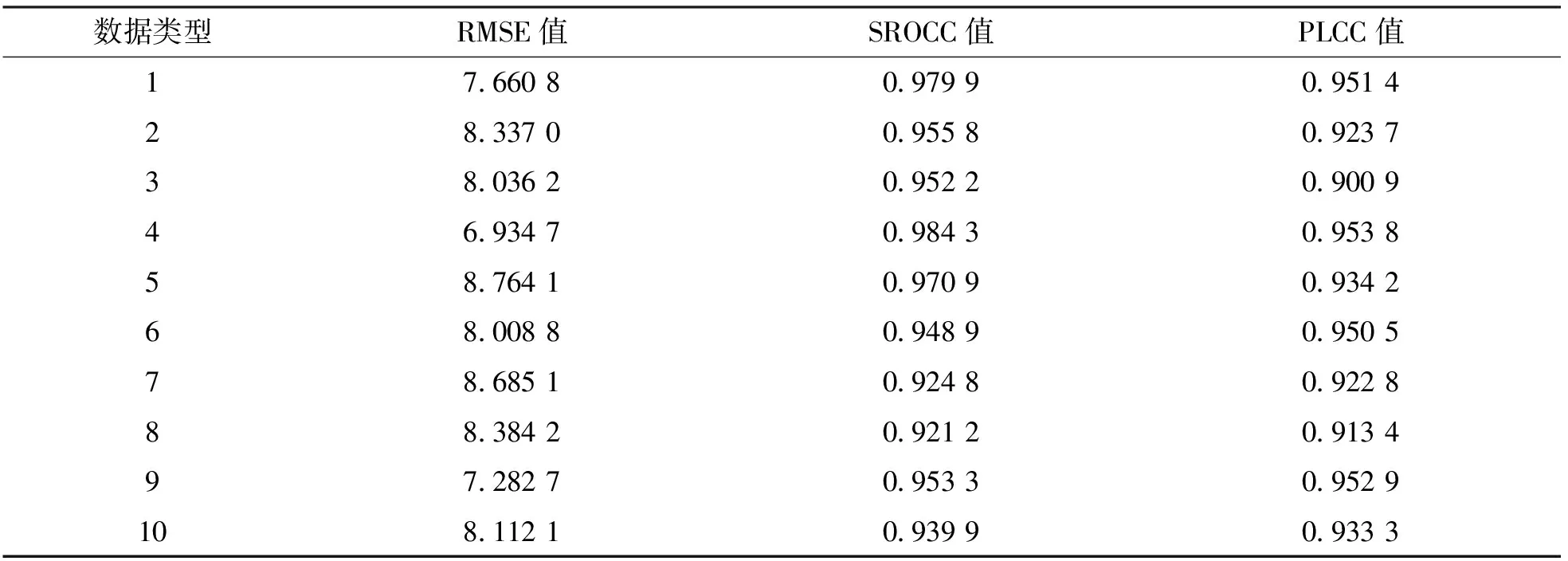
表2 本研究方法在不同数据类型上的图像质量评分

表2中的数据类型涉及交通工具、建筑、人物和自然场景等内容.表2结果表明, 本研究提出的方法所表现出的均方根差均小于9, 且其SROCC值指标和PLCC值在10种数据类型下的数值均在0.9以上, 其均值为0.953 1和0.933 7.说明本研究提出的算法能有效实现图像信息的提取, 具有较好的评价一致性.随后选择较为常见的盲图像质量评价方法与研究提出的方法进行对比, 并对每一类图像数据进行随机抽取, 以反复试验5次之后的结果中值为实验结果.此处用到的比较算法为无参考空间域图像质量评估算法(blind/referenceless image spatial quality evaluator, BRISQUE)、失真图像评估算法(distortion identification-based image verity and integrity evaluation, DIIVINE)、基于代码无参考评价算法(codebook representation for no-reference image, CORNIA)以及基于CNN的评估算法(image quality assessment-convolutional neural network, IQA-CNN).并借助相关评价指标对失真图像的预测结果进行一致性分析, 其结果见表3.

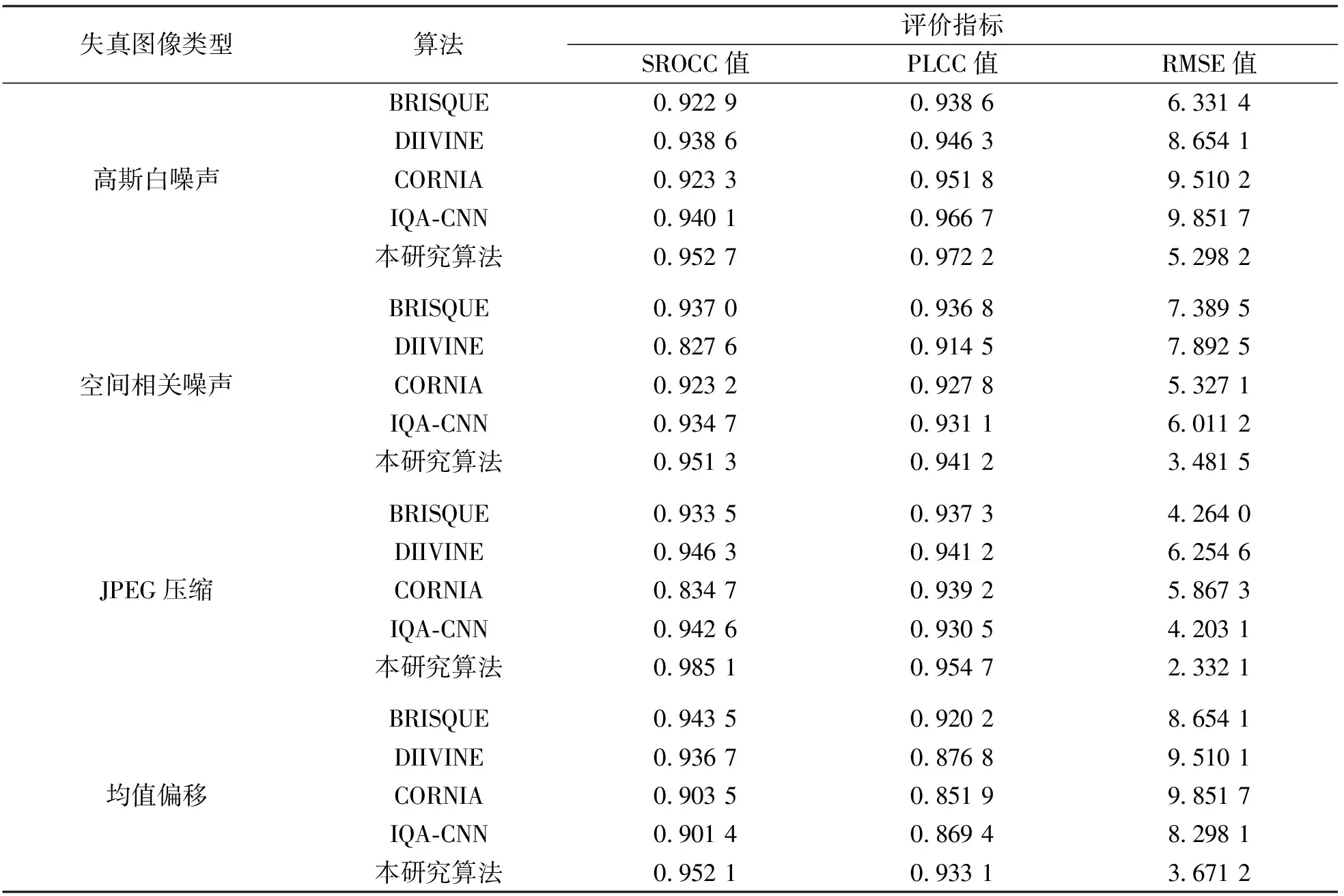
表3 不同算法的图像质量

表3结果表明, 在高斯白噪声失真图像中, SROCC值和PLCC值从大到小分别为: 本研究算法,IQA-CNN,DIIVINE,CORNIA,BRISQUE; 本研究算法,IQA-CNN,CORNIA,DIIVINE,BRISQUE.本研究提出的方法与IQA-CNN算法的质量效果与主观评价效果具有较高的一致性, 但本研究提出的方法的RMSE值(5.298 2)明显低于IQA-CNN算法(9.851 7).在空间相关噪声、JPEG压缩以及均值偏移3种失真图像中, 本研究提出的方法所表现的测试指标效果最好, 且其误差值均低于4, 其与最大均方根误差之间的差值幅度达到了38.77%,45.68%和62.73%.上述结果表明, 本研究提出的盲质量评价算法表现出较好的主观一致性, 且其预测结果与真实值之间的偏差较小, 能较好适应不同失真图像类型, 鲁棒性较强.随后对失真图像的均方根对比情况与预测分数之间的分布情况进行统计, 其结果见图6.

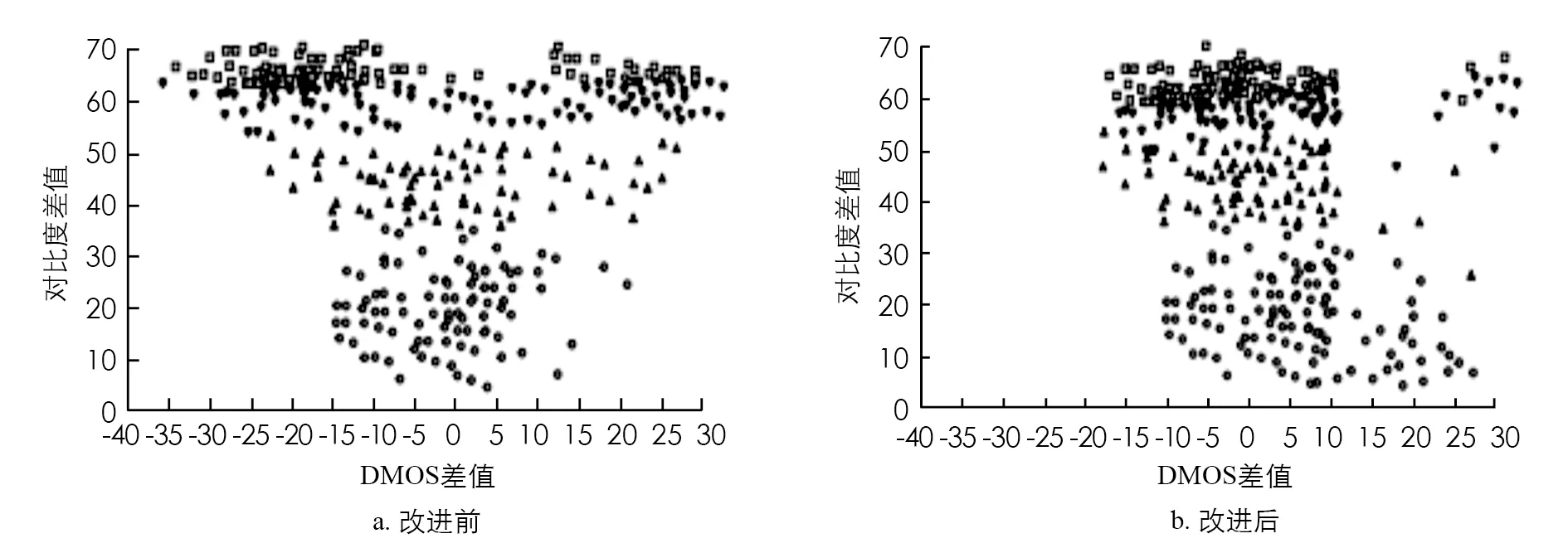
图6 失真图像的均方根对比情况与预测分数之间的分布情况

图6中横坐标表示图像DMOS值与预测质量分数的差值, 其数值越靠近0, 则表明其预测结果的偏差越小, 纵坐标表示图像对比度的差值, 其数值越大表明其对比度越小.图6结果表明, 本研究提出的算法对图像预测结果表现出较好的特征区别度, 其数值基本都靠近数值0, 较少受到噪声数据的影响.随后对模型的预测值与主观值的拟合结果进行分析, 其结果见图7.

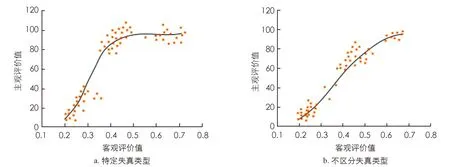
图7 失真图像类型下的模型预测值与主观值之间的拟合曲线

图7中的曲线和坐标点分别表示DMOS值和拟合曲线, 图7结果表明, 无论是否对失真图像类型进行划分, 本研究所提出的模型对图像质量评价的拟合效果均更好, 所表现出的聚集程度更为明显, 且主客观评价分值具有较高的一致性.

4 结论

本研究对CNN进行了改进, 通过引入残差结构以及图像子块置信度设置来实现对盲图像质量评价效果的提升, 并对本研究提出的方法进行检验, 结果表明本方法有效避免了数据的过拟合问题, 且其在256×256,128×128,64×64,32×32尺寸下的失真图像预测分数提升最大达到了3.88%,3.49%,3.51%,3.21%.在10种数据类型下, 本研究提出的方法的均方根差均小于9, 其SROCC指标和PLCC指标均值为0.953 1和0.933 7, 具有较高的评价一致性.同时在算法对比实验中, 本研究提出的算法在高斯白噪声失真图像中的SROCC指标和PLCC指标均最优, 其RMSE值(5.298 2)明显低于IQA-CNN算法(9.851 7), 在其他3种失真图像类型下的最大均方根误差比较差值幅度达到了38.77%,45.68%和62.73%, 图像预测偏差较小, 且其主客观评分拟合曲线受失真图像类型的干扰较小.考虑其他符合人眼视觉特性的图像质量评价指标是今后研究需要进一步改进的内容.