ICP与射频源的匹配网络的设计与实现

张 浩,蔡树向,刘 强,杨文广

(烟台大学机电汽车工程学院,山东 烟台264005)

电感耦合等离子体(ICP)自问世以来,就在化学分析特别是同位素分析领域有着重要地位,并且广泛应用于半导体加工制造中,如薄膜加工、等离子体刻蚀等。近年来,随着无线技术(如Wi-Fi、蓝牙和移动或无线物联网设备)的日益普及,越来越多的设备或系统采用射频电路[1-3]。为ICP提供能量的射频源设备,其输出阻抗一般为50或75 Ω,但等离子体的阻抗一般为几欧姆,且在一定范围内受到周围环境因素和仪器参数的影响而实时变化。如果将射频源直接与等离子体相连,传输线及器件中会存在大量的反射功率,降低射频源设备的工作效率,甚至于烧毁射频源设备。因此,需要在射频源设备和等离子体之间插入阻抗匹配装置,用以调节负载阻抗,使其与输出阻抗相匹配。在实际工况中,不同的工作设备负载阻抗的变化范围不尽一致,需要针对性地设计专用的阻抗匹配网络。现阶段阻抗匹配的算法主要有遗传算法、粒子群算法、模拟退火算法和神经网络算法等。理论上这些智能算法能够获得更好的匹配,但是其模型建立复杂,计算量较大,导致所需迭代时间长,同时智能算法使用的数字处理器增加了系统成本[3-4]。

本文首先基于ICP源的负载阻抗,确定匹配网络的类型,推导出先串后并和先并后串L型匹配网络中可变电容的电抗公式,说明负载阻抗对匹配网络选择的影响;其次通过Advanced Design System软件进行阻抗匹配仿真,详述阻抗匹配过程中可变电容变化趋势;最终设计出可以实时检测反射功率幅值和相位的互感检波电路。

1 匹配网络的选择及阻抗分析

常见的匹配网络有π型、T型和L型。π型和T型匹配网络不存在匹配禁区,但其三个自由度会使匹配目标函数变得更复杂,为函数的优化计算增加难度;且在匹配过程中需要控制三个可变器件动作,相比于L型网络,其使用的元件较多,总插入损耗更大,整个匹配网络的体积也会不可避免地增大[5]。L型网络由于所使用的元件最少、构造简单、损耗最小而被广泛用于射频阻抗设计,同时π型和T型匹配网络可以看做L型网络的级联,研究L型网络有着更基础的意义[6]。L型网络虽然存在着匹配禁区,但可以根据不同的负载阻抗特性选择不同的电感电容排列组合来获得合适的调节范围。L型网络有八种连接方式,如图1[7-8]。

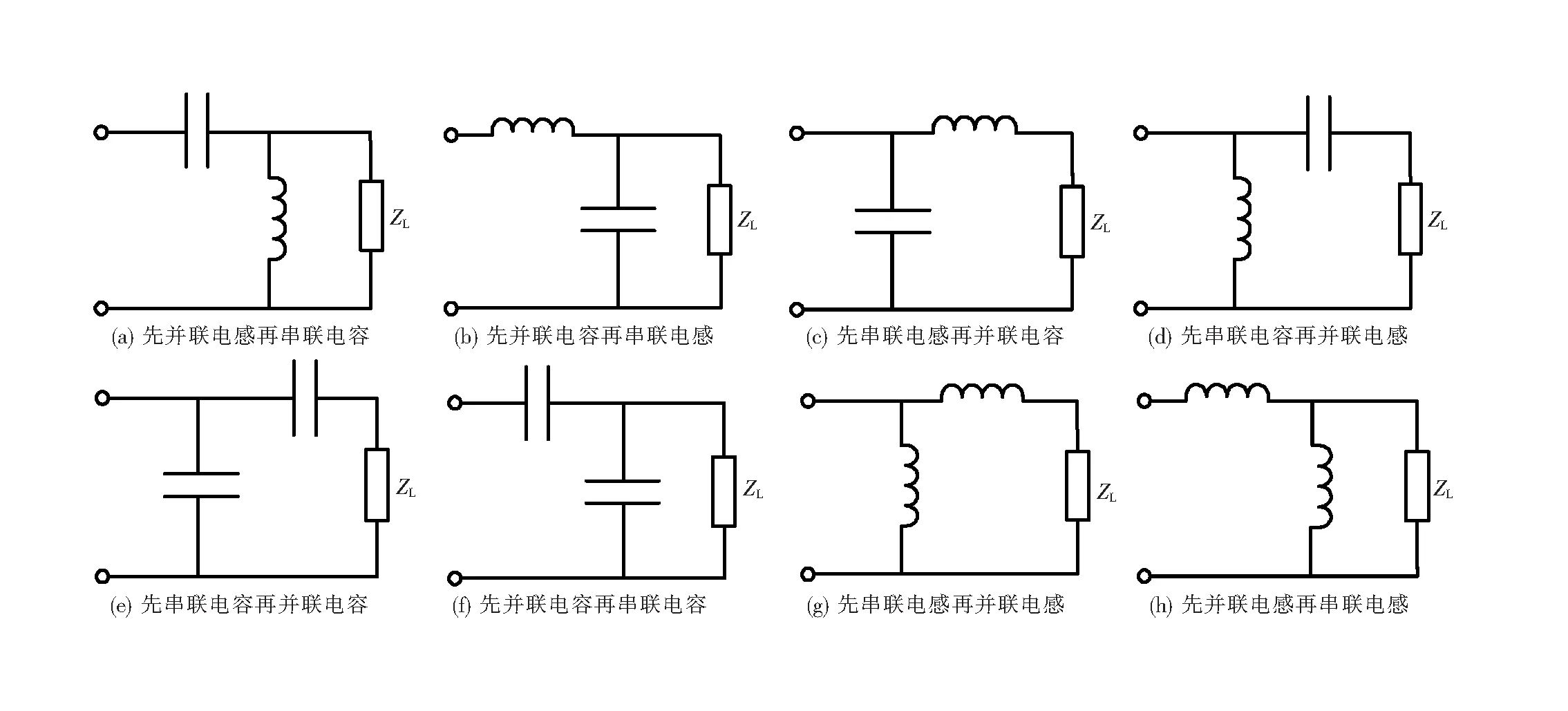
图1 L型网络连接

L型网络调节范围如图2。

负载阻抗落在1+jx圆内时,如图2(a):负载阻抗ZL先并联一个元件,使ZL移动到1+jx圆上,然后再串联一个元件,ZL沿着1+jx圆移动到Z0点。若是先并联电感再串联电容,移动路线为从A点到B点最后到D点,匹配网络如图1(a);若是先并联电容再串联电感,移动路线为从A点到C点最后到D点,匹配网络如图1(b)。

负载阻抗落在1+jb圆内时,如图2(b):ZL先串联一个元件,使ZL移动到1+jb圆上,然后再并联一个元件,ZL沿着1+jb圆移动到Z0点。若是先串联电感再并联电容,移动路线为从A点到B点最后到D点,匹配网络如图1(c);若是先串联电容再并联电感,移动路线为从A点到C点最后到D点,匹配网络如图1(d)。

负载阻抗落在1+jx和1+jb圆外的上半圆时,如图2(c):ZL可以先串联一个元件到达1+jb圆,然后再并联一个元件沿着1+jb圆到达匹配点Z0;ZL也可以先并联一个元件到达1+jx圆,然后再串联一个元件沿着1+jx圆到达匹配点Z0。若是先串联电容再并联电容,移动路线为从A点到B点最后到D点,匹配网络如图1(e);先串联电容再并联电感,移动路线为从A点到C点最后到D点,匹配网络如图1(d)。若是先并联电容再串联电容,移动路线为从A点到E点最后到D点,匹配网络如图1(f);若是先并联电容再串联电感,移动路线为从A点到F点最后到D点,匹配网络如图1(b)。

负载阻抗落在1+jx和1+jb圆外的下半圆时,如图2(d):ZL可以通过串联或者并联一个元件到达1+jb或者1+jx圆,然后再并联或者串联一个元件沿着1+jb和1+jx圆到达匹配点Z0。若是先串联电感再并联电感,移动路线为从A点到B点最后到D点,匹配网络如图1(g);先串联电感再并联电容,移动路线为从A点到C点最后到D点,匹配网络如图1(c)。若是先并联电感再串联电感,移动路线为从A点到E点最后到D点,匹配网络如图1(h);若是先并联电感再串联电容,移动路线为从A点到F点最后到D点,匹配网络如图1(a)。

然而在实际使用过程中,高精度电感的感抗调节过程较为复杂,且精准度没有可调电容高:滚筒电感的精度与电机齿数有关,且承载功率不大;磁控电感的调节曲线非线性,且控制难度较高;电感阵列的级数增大,其匹配精度会因为误差的累积而降低[4]。所以重点分析两电容分别串并联的方式构成的L型网络[9-10]。

负载阻抗可以看作电阻和电抗的串联[9-10],使用先串后并方式构成L型网络时,如图3所示,从源端向负载端看去,其阻抗为

(1)

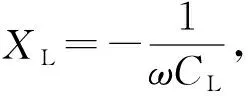
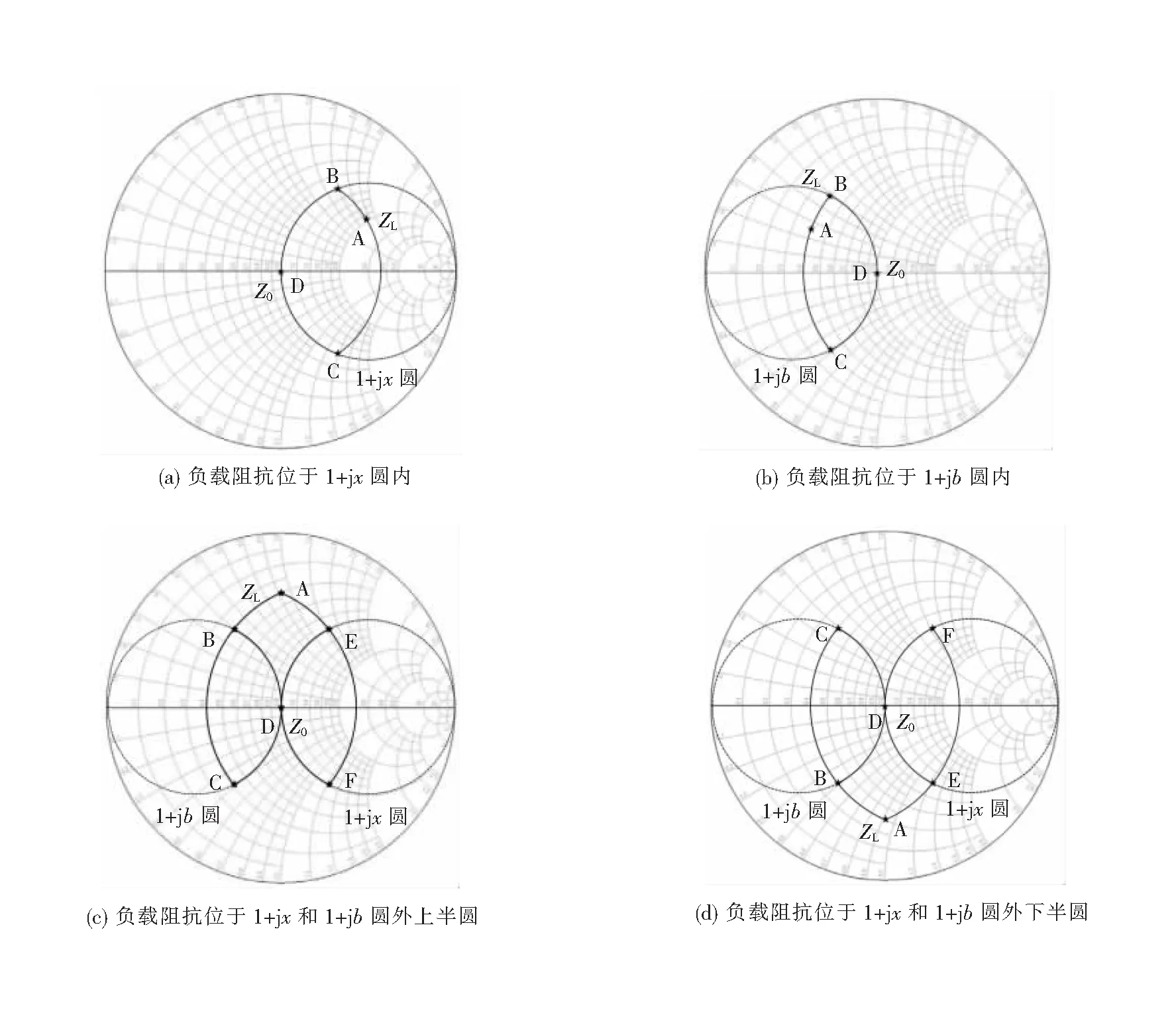
图2 L型网络调节范围

图3 先串后并负载阻抗等效

整个匹配网络的输入导纳为G,则

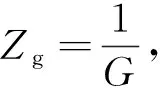
(2)

由式(1)、式(2)可得

(3)

式中:a和b分别为导纳的实部值和虚部值。

由式(3)可以看出,调节CT会对导纳的实部和虚部都产生影响,调节CL仅对导纳的虚部产生影响[11]。阻抗匹配网络的源端阻抗Z0=R0+j*0,故其源端导纳Z0=1/G0=1/R0+j*0。阻抗匹配时G0=G,就是调节CT、CL使G的实部等于1/R0,虚部等于0,即可完成阻抗匹配。

令

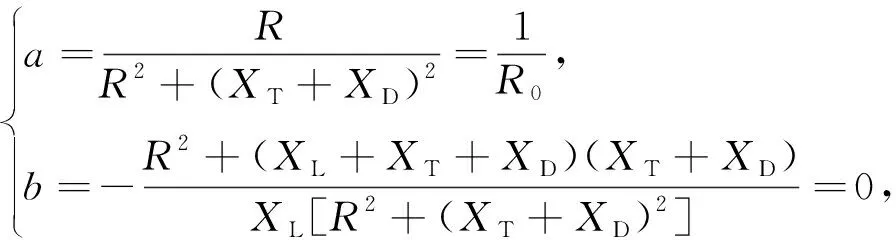
(4)

得

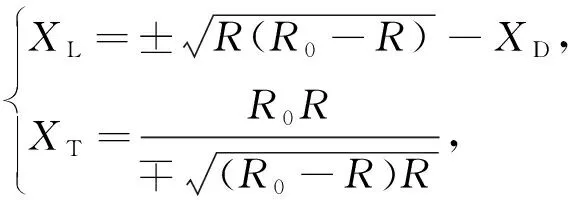
(5)

由式(5)可以看出,若是使用先串后并L型网络,需要保证R0>R。

同理,使用先并后串方式构成L型网络时,如图4所示,从源端向负载端看去,其阻抗为

(6)

简化得

解得

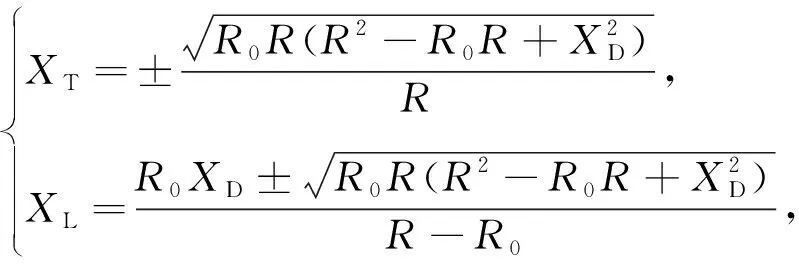
(8)

2 匹配网络仿真

ZL=R+jωLD=(2+j*85.2) Ω,

(9)

使用ADS(Advanced Design System)软件对其进行阻抗匹配仿真[12-14],结果如图5。

图4 先并后串负载阻抗等效

使用先串后并L型网络进行负载阻抗向源端匹配时,如图5(a),串联电容CT容值从5.12 nF减小至77.83 pF,负载阻抗沿等电阻圆从2+j*85.2变化到2+j*9.8,然后并联电容CL容值从0增大至575 pF,负载阻抗沿等电导圆从2+j*9.8变化到50+j*0。阻抗匹配完成后串联电容CT的容值约为77.83 pF,并联电容CL的容值约为575 pF[15]。

将R=2 Ω,LD=500 nH代入式(5),解得

使用先并后串L型网络进行阻抗匹配时,如图5(b),并联电容CL容值从0增大至55.16 pF,负载阻抗沿等电导圆从2+j*85.2变化到49.997+j*423.16;串联电容CT容值从272.71 pF减小至13.87 pF,负载阻抗沿等电导圆从49.997+j*423.16变化到50+j*0。阻抗匹配完成后串联电容CT的容值约为13.87 pF,并联电容CL的容值约为55.16 pF。

将R=2 Ω,LD=500 nH代入式(8),解得

由ADS匹配所得电容值与计算结果均相近。

从匹配结果可以看出,使用先串后并L型网络的电容容量变化较大,电容有从nF级到pF级的突变,给整个匹配电路的电容选择带来难度。而先并后串L型网络的电容容量变化较小,在匹配时控制单元对可变电容的调节也会更迅速,所以ZL=2+j*85.2时选用先并后串L型网络更加有利[16]。

3 匹配网络的硬件设计

匹配网络的硬件设计主体为自动阻抗匹配模块,其整体结构如图6。自动匹配时,负载的反射功率信号经定向耦合器的耦合线圈传递给互感检波电路,互感检波电路将检测到的幅值差以及相位差信号通过调理放大模块处理后传递给电机执行模块,电机动作调节可变电容容值,使系统反射功率逐渐减小,直到反射功率小于系统检出限,阻抗匹配完成。

图6 自动匹配模块整体结构

目前阻抗匹配中常用的可变电容有真空电容器、变容二极管和电容阵列。变容二极管可以无极调节,但是能承载功率小,不能承受过电压冲击,而且不能实现pF到nF甚至到μF的级间突变;电容阵列比较经济,但是阵列级数增加时,电容误差的累积会使整个匹配网络精度降低[17]。真空电容器损耗较小,在高频下额定电流较大,且对过电压有一定的自愈能力,承受瞬间的过电压不会产生永久性损坏;真空电容在几皮法到几千皮法均能实现高精度调节,拥有良好的调节范围,因此,选择真空电容作为匹配网络的可变电容器较为合适。

串联电容的容值对阻抗匹配的影响较大,微量的串联电容容值误差就会导致传输线中存在大量的反射功率,使阻抗匹配的过程失败。并联电容对阻抗匹配的影响稍小,一定量的误差并不会产生大量的反射功率。在匹配网络调节过程中,过电压会对可调电容造成不可逆转的损害,会使可变电容的调节范围变小。因此在串联电容CT的选择上,应选择调节精度高、单位电机转角对应电容量变化小的电容器;并联电容CL选择上,应选择调节范围较大、单位电机转角对应电容量变化大的电容器,以缩短阻抗匹配时间。其次可在CT、CL上各并联一个小容值的高压筒型陶瓷电容,用以增大CT、CL的调节范围和带负载能力。

在此理论基础上,本文设计的相位检测电路如图7(a)。相位检测电路中,反射功率在耦合线圈上产生互感电流,经TL1和TL2端口输入检波电路。检波二极管D1与电容C1以及电阻R1、可调电阻R3共同组成一个可低通滤波的包络检波电路。D1导通时,向C1充电,充电时间t=RDC(RD为二极管内阻);D1截止时,C1通过R1、R3放电,放电时间t=RLC(RL为C1并联电阻总和)。为避免产生惰性失真,在调幅波的任意一个周期内,C1通过RL的放电速度大于等于包络的下降速度。为了避免产生负峰切割失真,电路中使用R1和R3共同组成负载电阻RL。另外,R1和R2组成一电阻式分压器,分压器由一个高压电阻臂R1和一个低压电阻臂R2构成,电压从低压电阻臂侧流出[18-19]。

图7 互感检波电路

当源端阻抗虚部与负载阻抗虚部相等时,电压与电流同相位,电流经过耦合电容TCC,使得电流相位滞后电压相位90°,A点耦合电压值UA为0,所以R4、R5、R6中没有电流经过。可变电阻R3两端电流i1、i2值等于耦合线圈两端所输出的电流值,两者大小相等方向相反[20],所以R3的2号抽头电压为0,相位调节电压UT的值为0,电机不动作。当源端阻抗虚部与负载阻抗虚部不相等时,电压与电流相位有超前或者滞后,耦合电容TCC充电或者放电使得A点耦合电压值UA为正值或者负值,致使可变电阻R3两端电流i1、i2值不再大小相等方向相反,R3的2号抽头电压为正值或者负值,则会输出一个相位调节电压UT给电机[21]。

幅值检测电路如图7(b)。当源端阻抗虚部与负载阻抗实部相等时,幅值检测电路中B点电压与C点电压大小相等方向相反,则R10的2号抽头电势为0,幅值调节电压UL的值为0,电机不动作。当源端阻抗虚部与负载阻抗实部不相等时,若C点电压幅值大于B点电压幅值,则R10的2号抽头电势为正,幅值调节电压UL的值为正,输出一个正的幅值调节电压UL给下一级;若C点电压幅值小于B点电压幅值,则R10的2号抽头电势为负,幅值调节电压UL的值为负,输出一个负的幅值调节电压UL给下一级。

互感检波电路输出控制信号至电机后,电机控制可变电容动作,但是电机在每一次的转动过程中都会有微小的机械误差,在长期的匹配调节过程中机械误差会不断地累积,最终会导致匹配点的电容值偏移出可变电容的调节范围,整个匹配网络失去阻抗匹配的能力。因此在相位检测电路的基础上,还须相应地设计保护电路和手动调节电路,避免过电压施加到可变电容上,也便于匹配点超出调节范围时重新设置可变电容中心点。

4 总 结

通过对比不同阻抗匹配网络的特点,并结合阻抗匹配中ICP源的负载阻抗变化趋势,确定使用先并后串L型匹配网络;以此为基础提出自动匹配方法,并相应地设计出互感检波电路,此互感检波电路结构简单、反应灵敏;将检测到的反射功率的幅值相位信号通过电路处理后输出至电机,控制可变器件动作,最终完成匹配。整个阻抗匹配的过程为闭环控制,迅速高效。但在实际操作中仍有一些问题需要解决,例如供电电源会随高频信号产生振荡,匹配网络体积较大、需要小型化等等。这些问题需要在之后的实验中进一步地探究解决。