混合散射体的分解方法

王昱皓,曲风龙

(烟台大学数学与信息科学学院,山东 烟台 264005)

随着科技的不断发展,混合反散射问题已经被广泛应用到了雷达探测、声纳识别、医学成像和无损探伤。本文主要关注使用分解方法基于远场数据同时定位和反演混合散射体位置和形状的反散射问题。KIRSCH[1]对于Dirichlet边值的散射问题首次提出了分解方法,之后对于分解方法的研究有了很多出色的成果,文献[2]—[8]均使用分解方法对单一介质或障碍物的散射问题进行了研究,但在现实情况下,探测的物体是复杂多样的,因此,KIRSCH等[9]在先验假设下,研究了具有声软边界条件的障碍物和可穿透介质的混合逆散射问题,XIANG等[10]考虑了介质内有埋藏障碍物和外部不可穿透障碍物的混合逆散射问题。本文拟利用分解方法对一个可穿透介质和一个不可穿透障碍物的混合散射问题进行研究,希望将混合散射问题扩展到具有复杂边界条件的情形。

1 准备知识

定义D1⊂3为可穿透非齐次介质,D2⊂3为不可穿透障碍物且D1∪D2=∅(图1),折射指数满足Re[n(x)]>0并且Im[n(x)]≥0。总场为u,入射场为ui=eikx·d,散射场为us=u-ui,其中k为波数,d∈2为入射方向。根据散射体的不同性质,折射指数是不相同的,因此先验假设在非齐次介质D1中Re[n(x)]>1且在齐次背景介质中n(x)=1。混合散射模型可由方程组(1)表示,

(1)

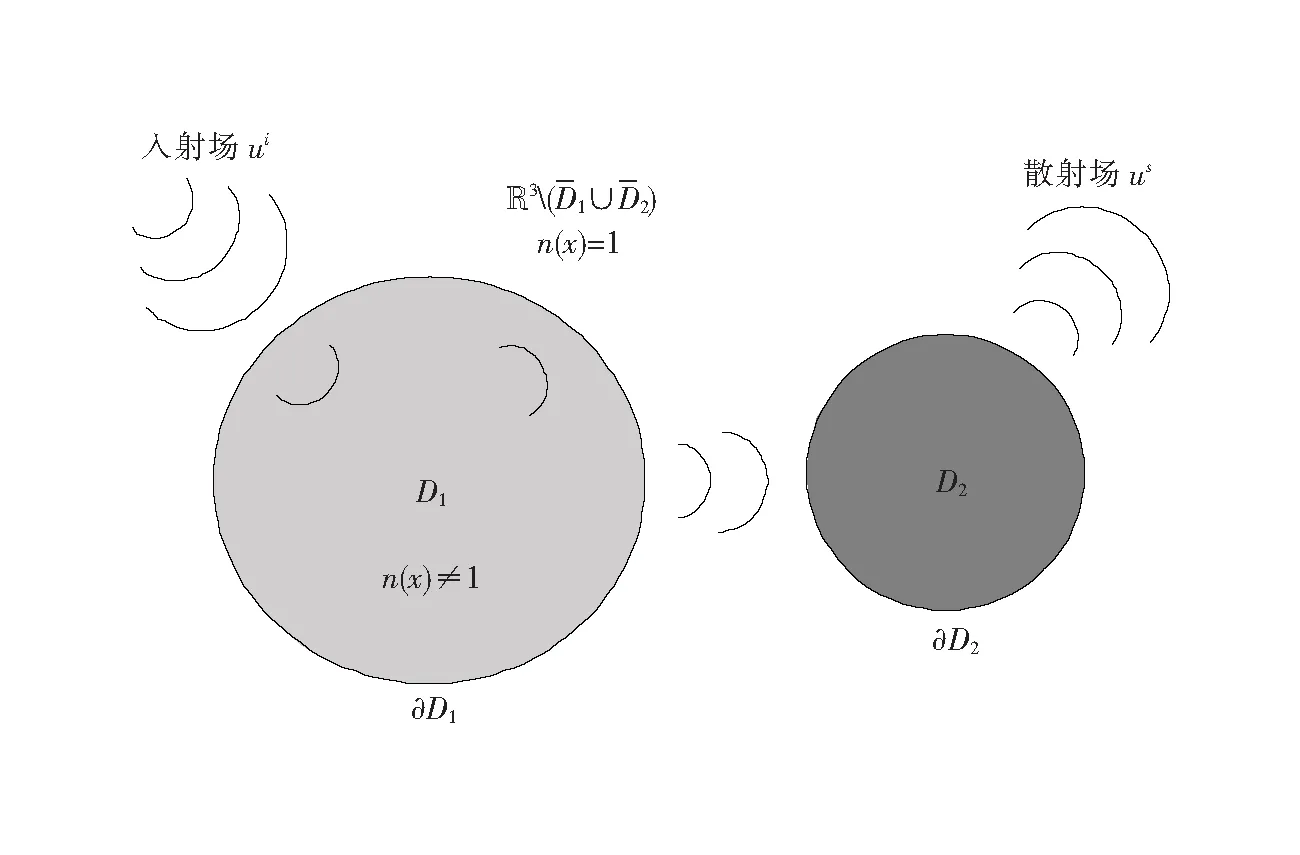
图1 混合散射模型

(2)

(3)

2 正散射问题

本节将用变分方法证明问题(1)—(2)对应的解的适定性。由于入射场ui在全空间满足Helmholtz方程Δu+k2u=0,令(u,v):=(us,vs),得到如下边值问题:

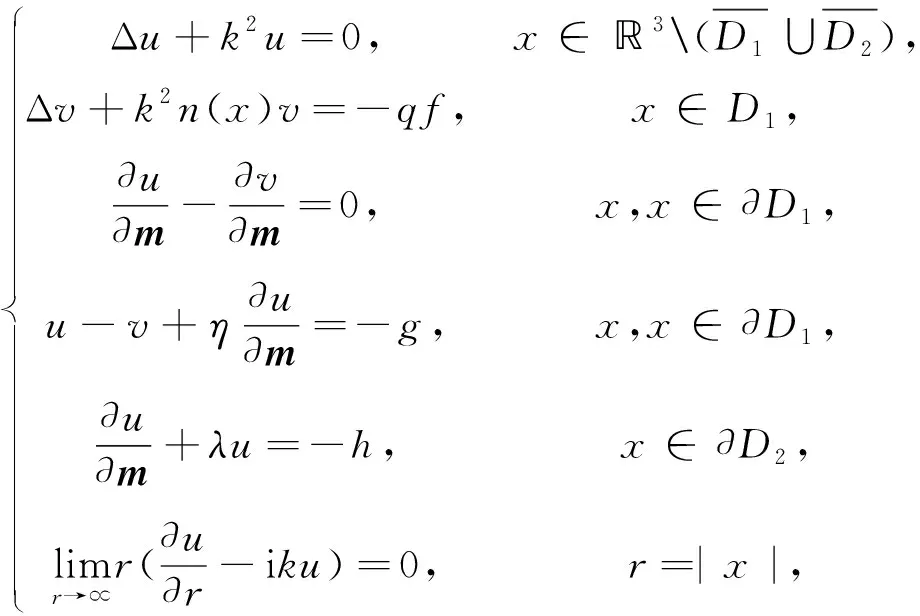
(4)

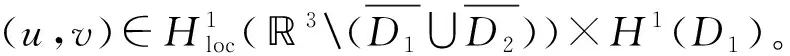
(5)

下面介绍映射N的重要性质,见文献[13]。

应用格林定理,将问题(4)转化为一个变分问题,找解w:=(u,v),满足如下变分形式:

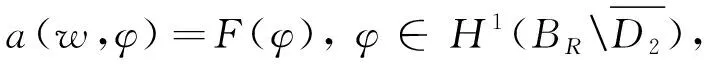
(6)

这里

令

a(w,φ)=:a1(w,φ)+a2(w,φ)=F(φ),

(7)

其中,

由引理1得

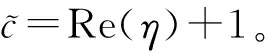
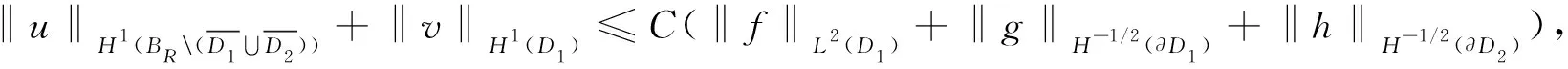
(8)

这里C是只与半径R有关的正常数。

3 逆散射问题

根据定理3,引入解算子G:Y→L2(2),定义为

G(f,g,h)T=u∝,

(9)

这里,Y:=L2(D1)×H-1/2(∂D1)×H-1/2(∂D2)且u∝是问题(4)的解u对应边界数据(f,g,h)T∈Y的远场模式。

引理2 算子G是紧的并且在L2(2)中是稠密的。

证明算子G的紧性可由椭圆方程的内部正则性结果得到。只需要证明G的共轭算子G*是单射即可证明G在L2(2)中是稠密的。

令(w,p)为问题(4)的解,(u,v)为问题(1)对应入射场:

的解。

由格林定理,得

因此有

(10)

由于us=u-ui和w都满足散射条件,于是有

将其代入式(10),利用边界条件,有

(11)

z∈(D1∪D2)⟺φz∈R(G),

这里R(G)表示G的值域。

和函数wz(x)=χ(|x-z|)Φ(x,z),x∈3。

显然,wz(x)∈C∝(3)是问题(4)的解,因此

为了使用分解方法,引入远场算子F:L2(2)→L2(2),形式如下:

(12)

显然,Fg是入射Herglotz波函数

(13)

对应的远场模式。

接下来定义入射算子H:=(H1,H2,H3)T:L2(2)→Y,形式如下:

(14)

根据叠加原理和算子G的定义,可知F=GH。

下面引入如下定义的算子:

其中i,j=1,2。根据迹算子的有界性可知上述算子均有界。

定理4 远场算子F可以分解成如下形式:

F=GT*G*,

(15)

中间算子T:Y→Y*为

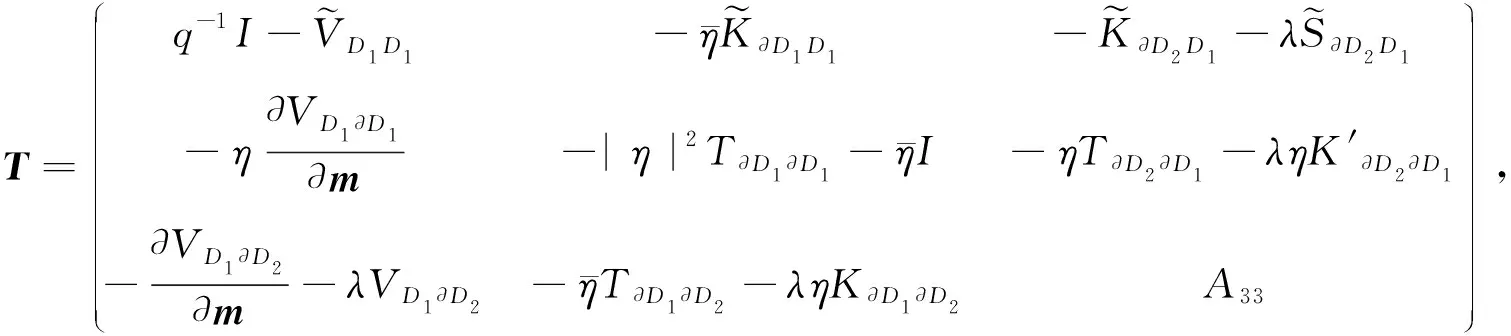
(16)

证明根据式(14)可以得到H的共轭算子H*:L2(D1)×H-1/2(∂D1)×H-1/2(∂D2)→L2(2)有如下形式:

(17)

可以看出,式(17)是函数

(18)

的远场模式并且也是问题(4)对应边值数据

的解。

由于已知H*=GT,那么H=T*G*。定理得证。

为了证明分解方法,需要证明式(16)中的分解满足定理5。

定理5 中间算子T满足如下性质:

1) 如果k2既不是-Δ在D2中的Dirichlet特征值也不是Neumann特征值,那么T:Y→Y*是同构的;

2)T=T1+T2,其中当Re[n(x)]>1时T1是强制的,T2是紧的;

3) Im(T)是非正且紧的,即Im〈Tφ,φ〉≤0,φ∈Y。

证明首先证明性质1)和2)。显然,T可以分解成

现在证明性质3)。根据定理4,有

I1+I2+I3+I4+I5+I6。

显然,因为Im[n(x)]≥0,Im(η)≤0,可以得到

接下来利用格林定理,跳跃关系和渐近关系对每一项进行分析有

I6=-λ〈W+,φ3〉∂D2=〈W-,λφ3〉∂D2-λ〈φ3,φ3〉∂D2,

那么得

因此,

这里γ=eikR/4πR。定理得证。

定理6φz定义同定理3。假设k2既不是-Δ在D2中的Dirichlet特征值也不是Neumann特征值并且在D1中Re[n(x)]>1,那么就有

(19)

这里{λj;ψj}j∈是自伴随算子F#:=|Re(F)|+|Im(F)|的特征系统,W(z)为指标函数。

4 数值结果

这一节给出一些数值反演的结果,以证明提出的数值算法是有效和适用的。以下给出的所有数值结果,均在有限的入射方向和观测方向下利用积分方程方法进行数值反演。

数值反演所需要图形的几何参数见表1。

表1 几何参数

为了更加简洁地表示,本文所展示的数值例子都设置成相同的参数,见表2。

表2 相关参数设置

例1 考虑根据远场数据同时重建具有导电传输边界条件的圆形介质的边界∂D1和具有阻抗边界条件的圆角方形障碍物的边界∂D2,见图2。

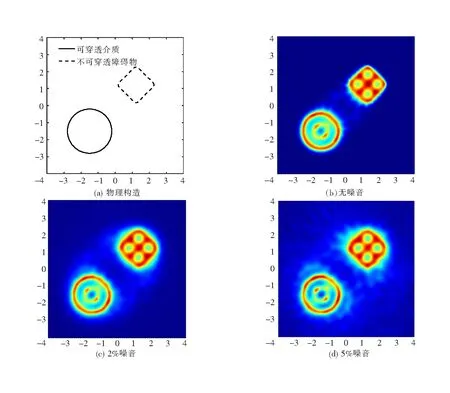
图2 同时重建圆形介质和圆角方形障碍物

例2考虑根据远场数据同时重建具有导电传输边界条件的圆形介质的边界∂D1和具有阻抗边界条件的圆角三角形障碍物的边界∂D2,见图3。

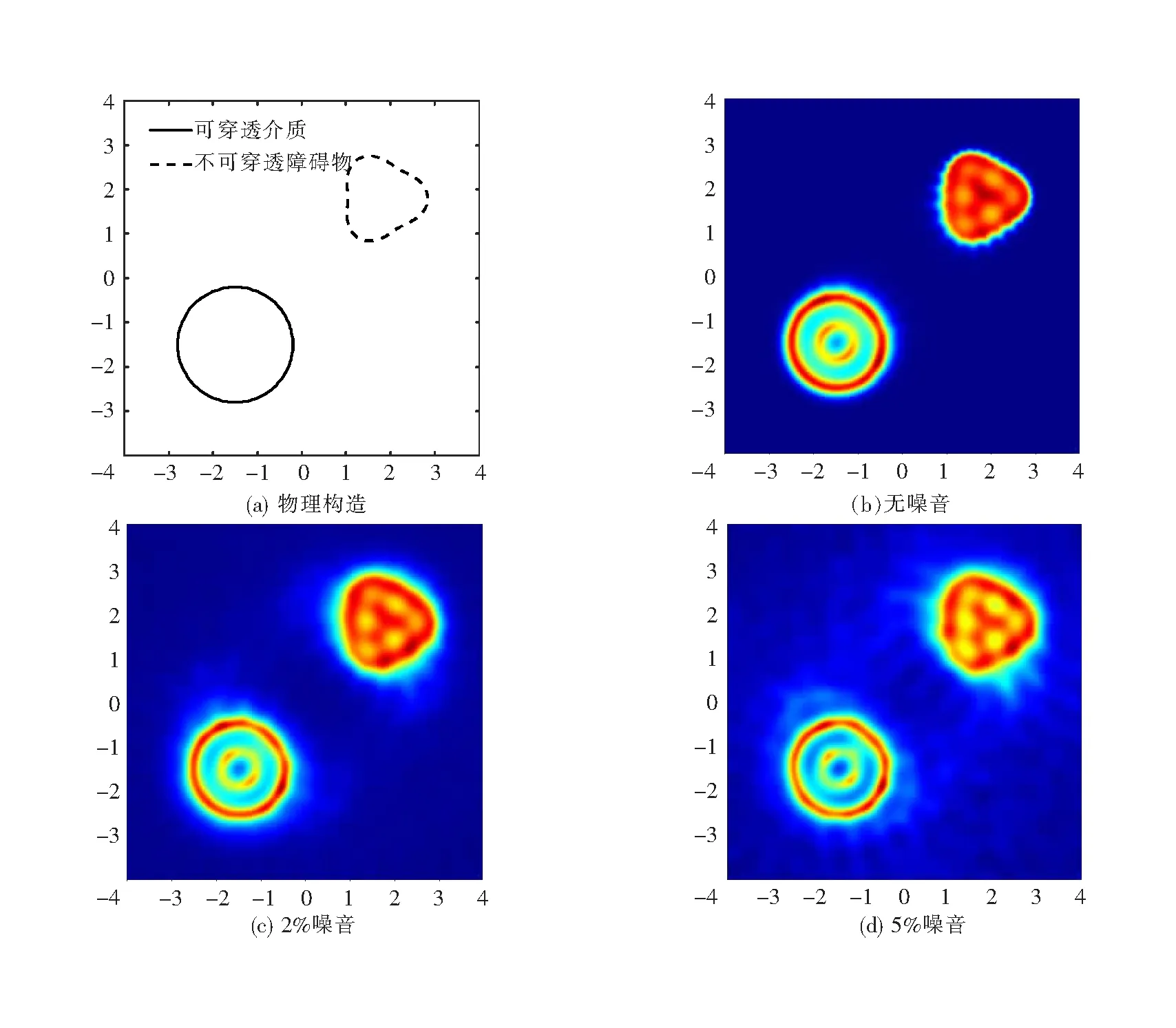
图3 同时重建圆形介质和圆角三角形障碍物

例3考虑根据远场数据同时重建具有导电传输边界条件的风筝形介质的边界∂D1和具有阻抗边界条件的圆角方形障碍物的边界∂D2,见图4。

图4 同时重建风筝形介质和圆角方形障碍物

通过以上部分数值算例的展示,可以看出本文所提出的数值算法在相同的探测参数下对不同形状的混合散射体都有很好的反演效果,可以很明显地反演出混合散射体的形状和位置,这证明了数值算法的有效性和适用性。