两维FFT和VD-DPT算法结合的LFM信号参数估计方法
2023-07-14庞存锁苏灿生
庞存锁,苏灿生,张 硕,2
(1 中北大学信息与通信工程学院,山西 太原 030051;2 中北大学信息探测与处理山西省重点实验室,山西 太原 030051;3 中北大学电子测试技术国家重点实验室,山西 太原 030051)
0 引言
线性调频信号(LFM)参数估计在雷达、声纳、成像等领域应用广泛,相关研究文献较多,如文献[1-2]研究了基于分数阶傅里叶变换(FRFT)和相位差结合的LFM信号参数估计方法;文献[3]研究了基于改进S变换和短时傅里叶变换(STFT)自适应窗长相结合的线性频率调制连续波信号(LFMCW)的参数估计方法;文献[4]研究了基于两维搜索的二次调频信号参数估计方法;文献[5-6]研究了基于FRFT的多分量线性频率调制信号(LFM)参数估计方法;文献[7]研究了基于改进精估计与FRFT结合的Chirp信号参数估计方法;文献[8-10]研究了基于离散多项式相位变换(DPT)的LFM参数估计方法;文献[11]研究了基于分段处理和FRFT结合的LFM参数估计方法;文献[12]研究了基于短时相干积分和非相干累加的LFM信号参数估计方法;文献[13]研究了基于自相关函数和Dechirp结合的LFMCW参数估计方法;文献[14-15]研究了基于吕分布(LVD)与FRFT结合的参数估计方法;文献[16]研究了基于时频分布的LFM参数估计方法。
总结上述研究方法,可将LFM信号参数估计方法分为两大类,其中第一类以最大似然估计思想为主,如FRFT、Dechirp以及二维搜索等,这类方法的参数估计精度高,但运算量普遍较大;第二类以降维思想为主,如DPT、LVD、相位差分、时频分布等,这类方法运算量较小,但低信噪比下参数估计误差大。针对第二类方法,为了解决低信噪比下,长序列LFM信号参数估计精度和运算效率的问题,文中提出基于两维FFT和VD-DPT算法结合的LFM信号参数估计方法,首先将信号进行两维分解,接着对信号的调频率参数利用VD-DPT方法进行初步估计,最后以此为基础利用Dechirp方法,对两维数组进行最大值寻优处理,以快速获得LFM信号参数。
1 信号模型
设LFM信号的一般表达式为[9,11]:
(1)
其数字离散形式可表示为:
(2)
式中:A为信号幅度;f0为信号初始频率;k为信号调频率;T为采样间隔;n为总采样点数。
将式(2)进行分段处理后组成两维数组,即:
(3)
式中:l∈[1,L-1];m∈[0,M-1];L=N/M为信号的分段数,M为段内信号的点数,M和N都满足2的幂次方,其中M的长度可结合先验信息和文中后续方法进行选择。
1.1 行信号的相位和频率特征
式(3)中s(l,m)可写为:
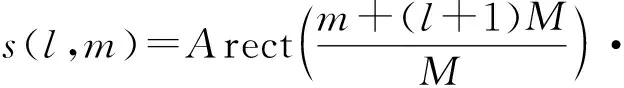
(4)
式(4)中s(l,m)相位为:
φ(s(l,m))=2πf0(m+(l-1)M)T+
πkT2(m2+2m(l-1)M+(l-1)2M2)
(5)
由式(5)可得,行内信号的频率可表示为:
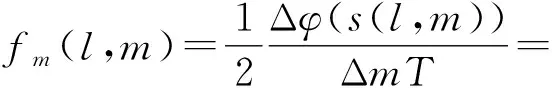
(6)
由式(6)可知,行内信号的频率差为:
fm(l,Δm)=fm(l,m+Δm)-fm(l,m)=kΔmT
(7)
1.2 列信号的相位和频率特征
由式(5)可得,列内信号的频率可表示为:
(8)
由式(8)可知,列内信号的频率差为:
fl(Δl,m)=fl(l+Δl,m)-fl(l,m)=kΔlMT
(9)
设行内信号的频率在整段间的走动不超过频率分辨单元fs/(2M),则从式(9)可知,fl(Δl,m)需要满足:
(10)
式中fs=1/T,为信号的采样频率。
将式(9)代入式(10)可得:
(11)
2 LFM信号的两维频谱特征和VD-DPT参数估计方法
2.1 两维LFM信号中行和列的频谱特征
图1为所提算法的处理流程。
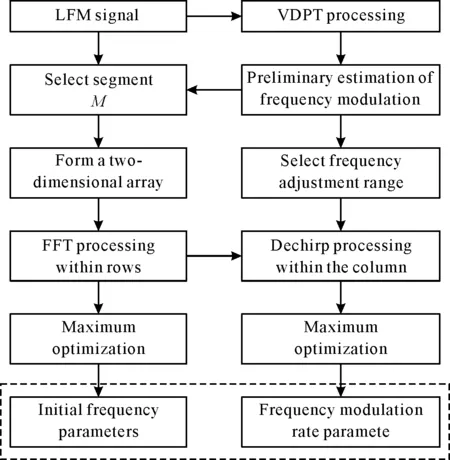
图1 文中算法流程Fig.1 Algorithm flow of this paper
对式(3)关于行信号进行FFT变换,则有:
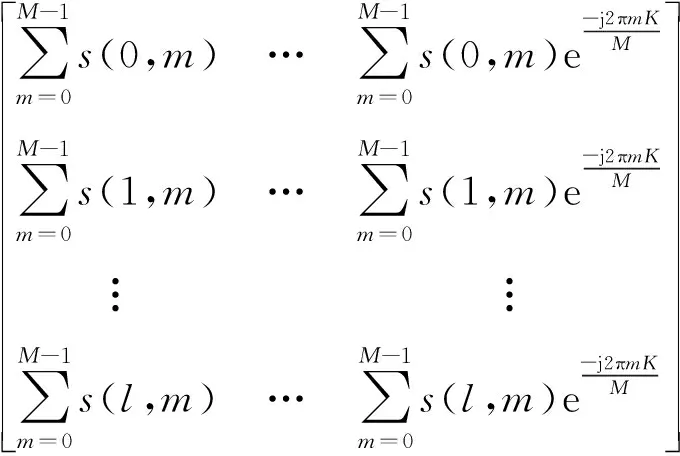
(12)
式中:k∈[0,M-1],且如果行间信号频率走动满足式(10),设S(l,K)|l最大峰值处对应的频率点为mf,则获得的信号初始频率可表示为:
(13)
对式(12)按列关于m进行FFT变换,则有:
S(J,K)|l,m=FFTm(FFTl(s(l,m)))
(14)
2.2 基于VD-DPT的LFM信号调频率估计
为了消除多普勒频谱扩散引起的LFM信号参数估计难的问题,利用VD-DPT方法对k进行初步估计,然后在此基础上进行Dechirp处理。
将式(2)进行DPT运算,可得:
(15)
式中:τ为信号的时延;C(n,τ)是关于(n,τ)的函数,文献[4-5]对τ进行了分析,指出τ=0.5N时,调频率参数估计精度高,但输出信噪比低。为了提高低信噪比下LFM信号的调频率参数初估计值,综合考虑不同时延 的影响,对式(15)进行VD-DPT处理,并结合阈值门限TH,将获得的调频率参数kq进行平均处理,即:
(16)
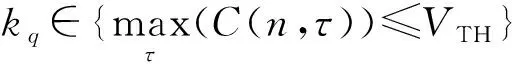
(17)

3 不同参数对算法的影响分析
3.1 对算法的影响
设待测LFM信号的初始频率为100 Hz,调频率为50 Hz/s,采样间隔为200 μs,信号长度为2 560点,输入信号信噪比范围为-15~-5 dB。图2显示了不同信噪比下,τ与检测概率、调频率参数估计误差之间的关系,从中可以看出τ越小,检测概率越大,越有利于低信噪比信号的检测,相比于DPT(τ=N/2)方法信噪比提高约2~3 dB;但τ越小时,调频率估计的相对误差越大。为此,综合考虑τ的影响,选取τT=(0.1~0.3)NT。
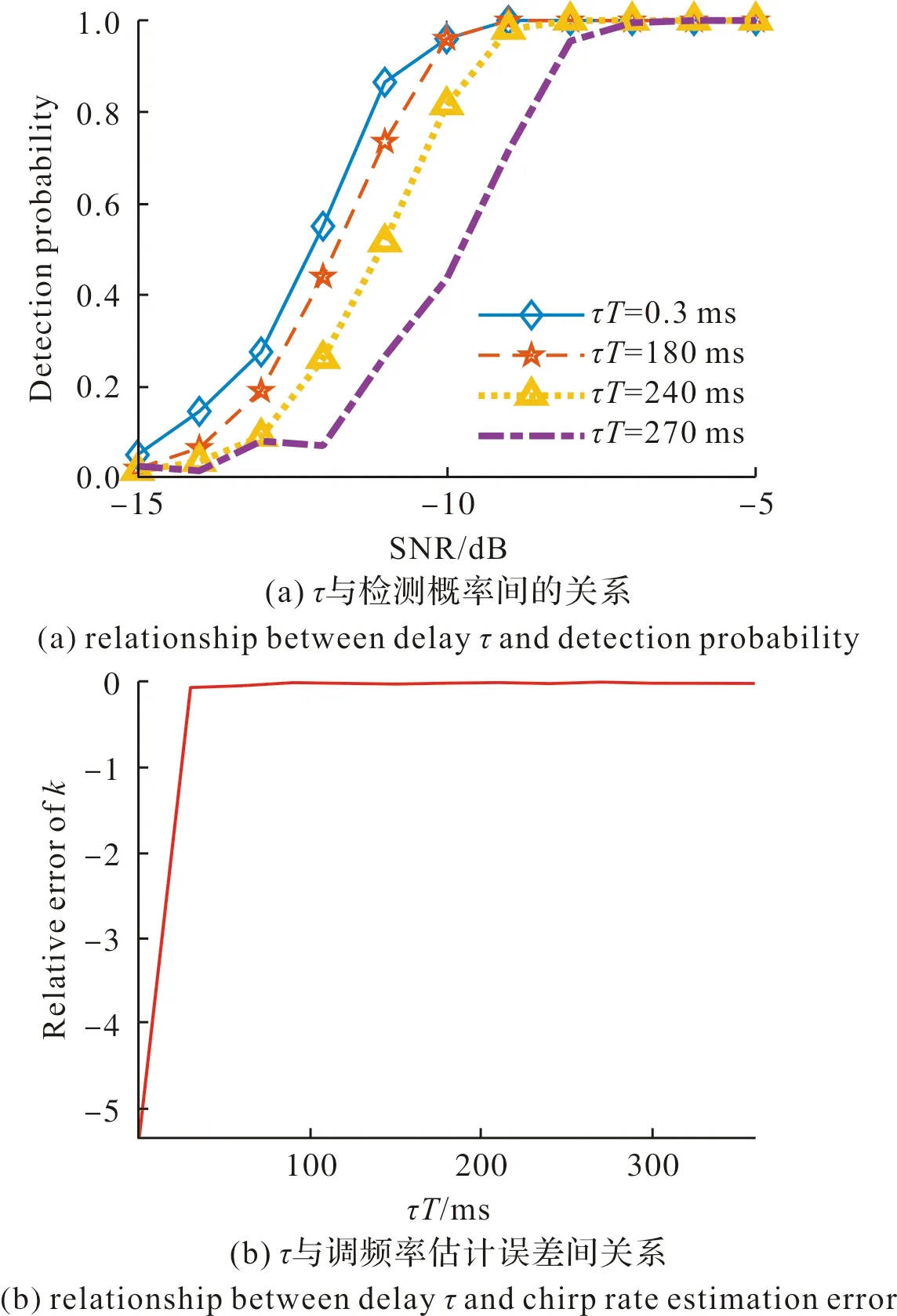
图2 τ与检测概率及调频率误差之间的关系Fig.2 Relationship between delay τ, detection probability, and chirp rate error
3.2 M对算法的影响
设信号参数同3.1节,图3给出了M为32,128时,利用式(12)、式(14)获得的信号两维频谱分布图,为了提高行间信号的频率显示分辨率,这里统一补零后按照256进行运算。
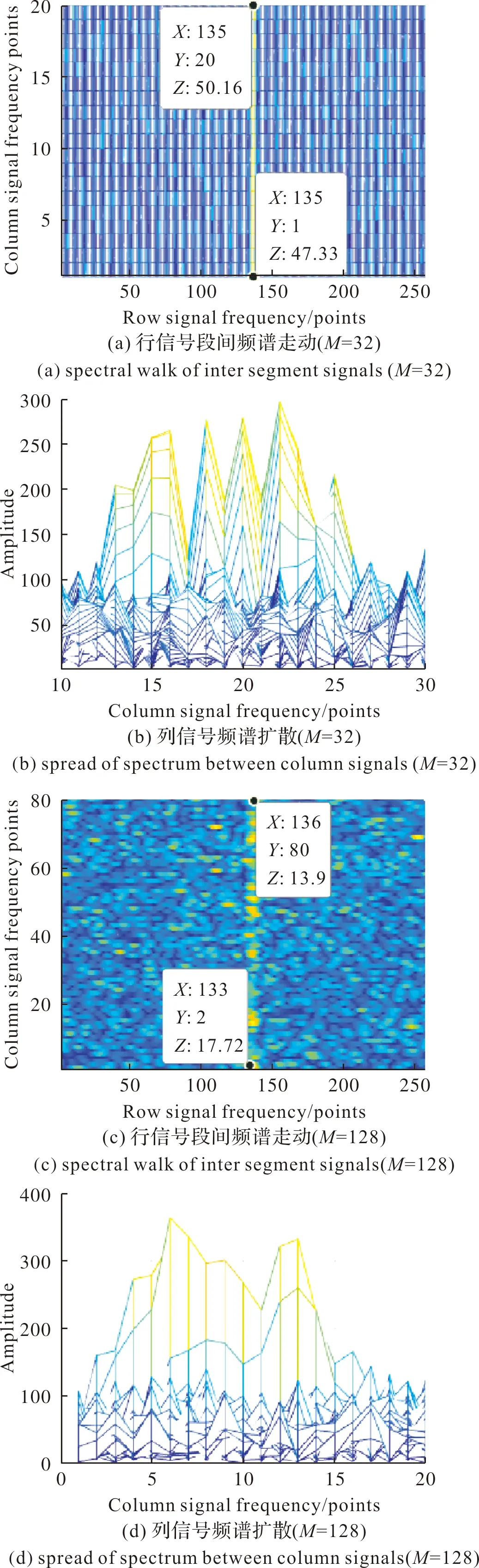
图3 M对信号检测的影响Fig.3 The impact of M on signal detection
其中,图3(a)、图3(b)显示了M=32时,行信号(对应X轴)在段间的频谱处于同一条直线上,没有发生频谱走动,但由于调频率的影响,列信号(对应Y轴)的频谱出现了走动;图3(c)、图3(d)显示了M=128时,行信号(对应X轴)在段间的频谱已经出现了距离单元的走动,同时由于调频率的影响,列信号(对应Y轴)的频谱出现了严重的扩散现象。因此,M的大小对算法检测性能有较大影响,实际中M首先结合先验信息取较小值,然后在式(11)基础上进行调节。
4 仿真验证分析
4.1 不同算法检测性能分析
设信号仿真参数同3.1节,信噪比为-12 dB。图4给出了直接FFT、DPT(τ=N/2)、VD-DPT(变时延τ)算法处理结果。
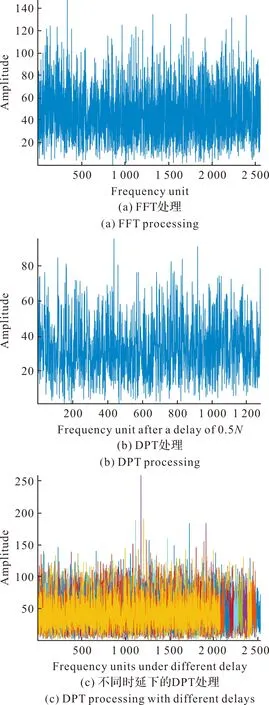
图4 不同算法处理结果比较Fig.4 Comparison of processing results of different algorithms
从图中可以看出,图4(a)在低信噪比下,无法对信号进行可靠检测;图4(b)利用最大值对应点进行估计后,调频率参数为1 376.6 Hz/s,与理论值50 Hz/s相差较大,已无法进行合理的预估;图4(c)显示不同延时(0.1N~0.3N)下,目标信号可以被看到,利用式(15)~式(17)可得调频率参数的初估计值为45.6 Hz/s,与理论值50 Hz/s基本一致,将其代入式(11)计算后得M为106,这里综合考虑取两维数组中M为64;图5给出了直接两维FFT和建议算法的处理结果。其中,图5(a)显示了直接两维FFT处理后目标信号无法看到,但经过Dechirp处理后,图5(b)可清晰显示出目标信号,利用峰值最大点并结合式(13)、式(18),可得信号频率估计值为104.2 Hz,调频率为50.1 Hz/s,这与理论值基本一致。
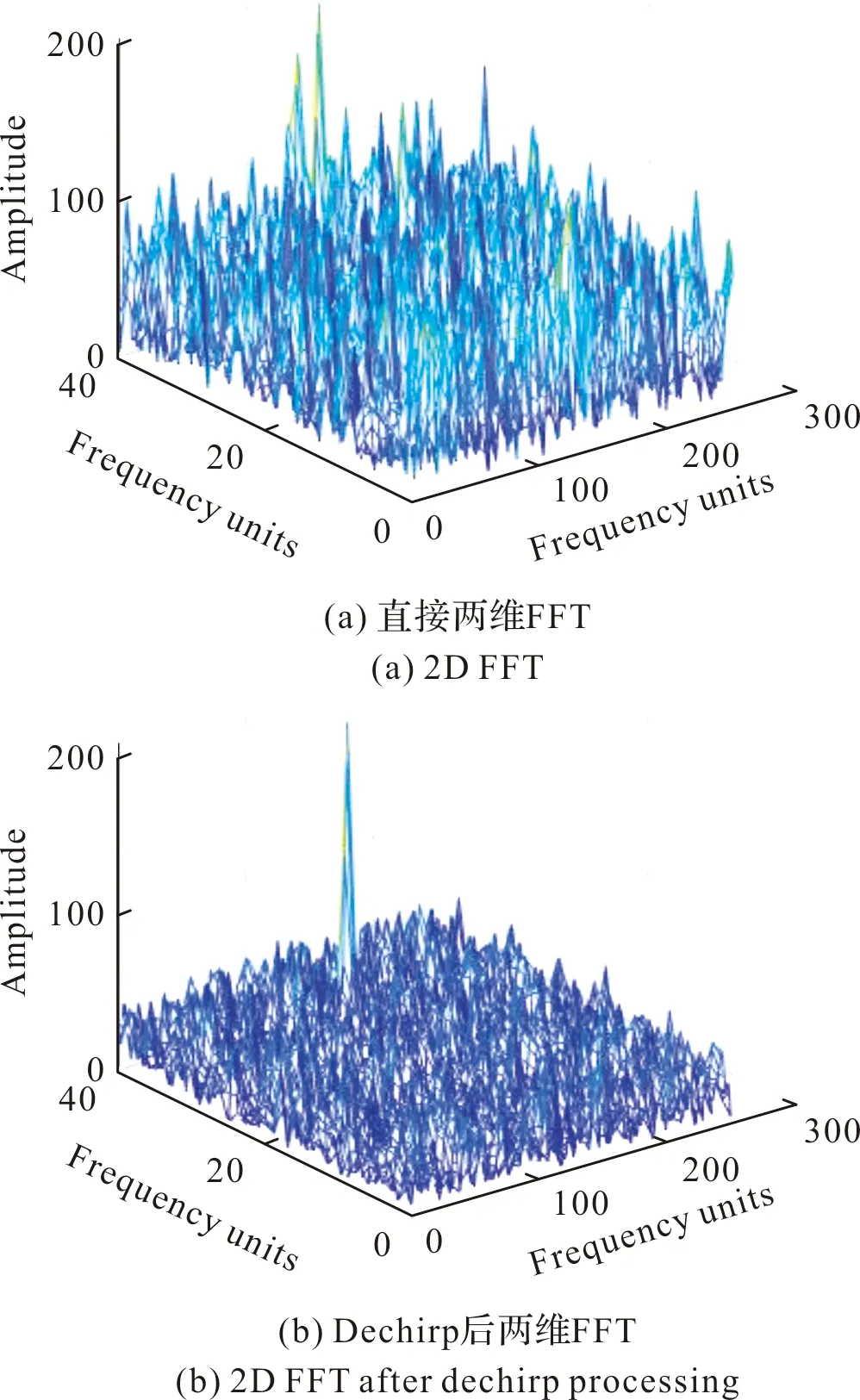
图5 两维FFT后处理结果Fig.5 Processing results after 2D FFT
4.2 不同算法运算量分析
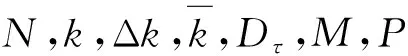
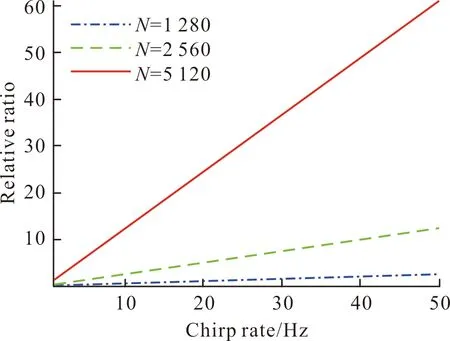
图6 不同调频率下的复乘运算量比较Fig.6 Comparison of complex multiplication operations under different chirp rates
5 实测弹丸数据分析
为了进一步验证算法的有效性,利用连续波雷达采集弹丸信号验证建议算法的检测性能,其中高加速弹丸信号回波信号近似为LFM信号[9]。雷达工作在S波段,采样频率为78 kHz,积累时间为200 ms,加入的高斯白噪声为-20 dB,P=64。图7为不同算法的处理结果,其中图7(a)为FFT处理结果,图7(b)为文献[8]处理结果,图7(c)为建议算法处理结果。对比图7结果可知,建议算法在低信噪比时,检测性能具有明显的优势。
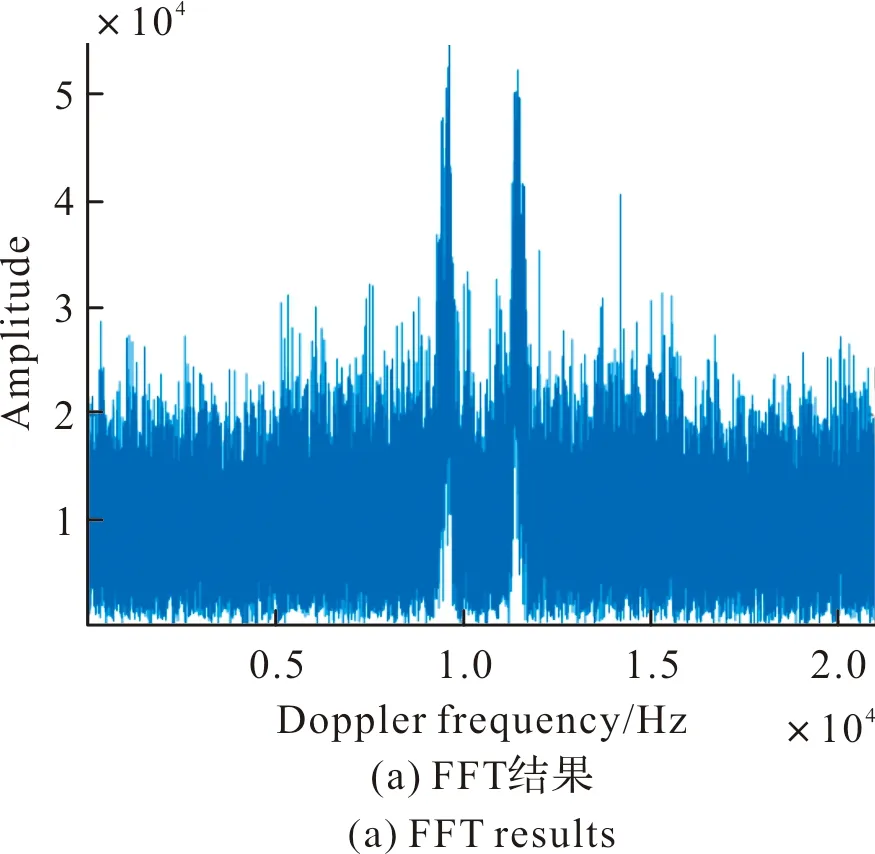
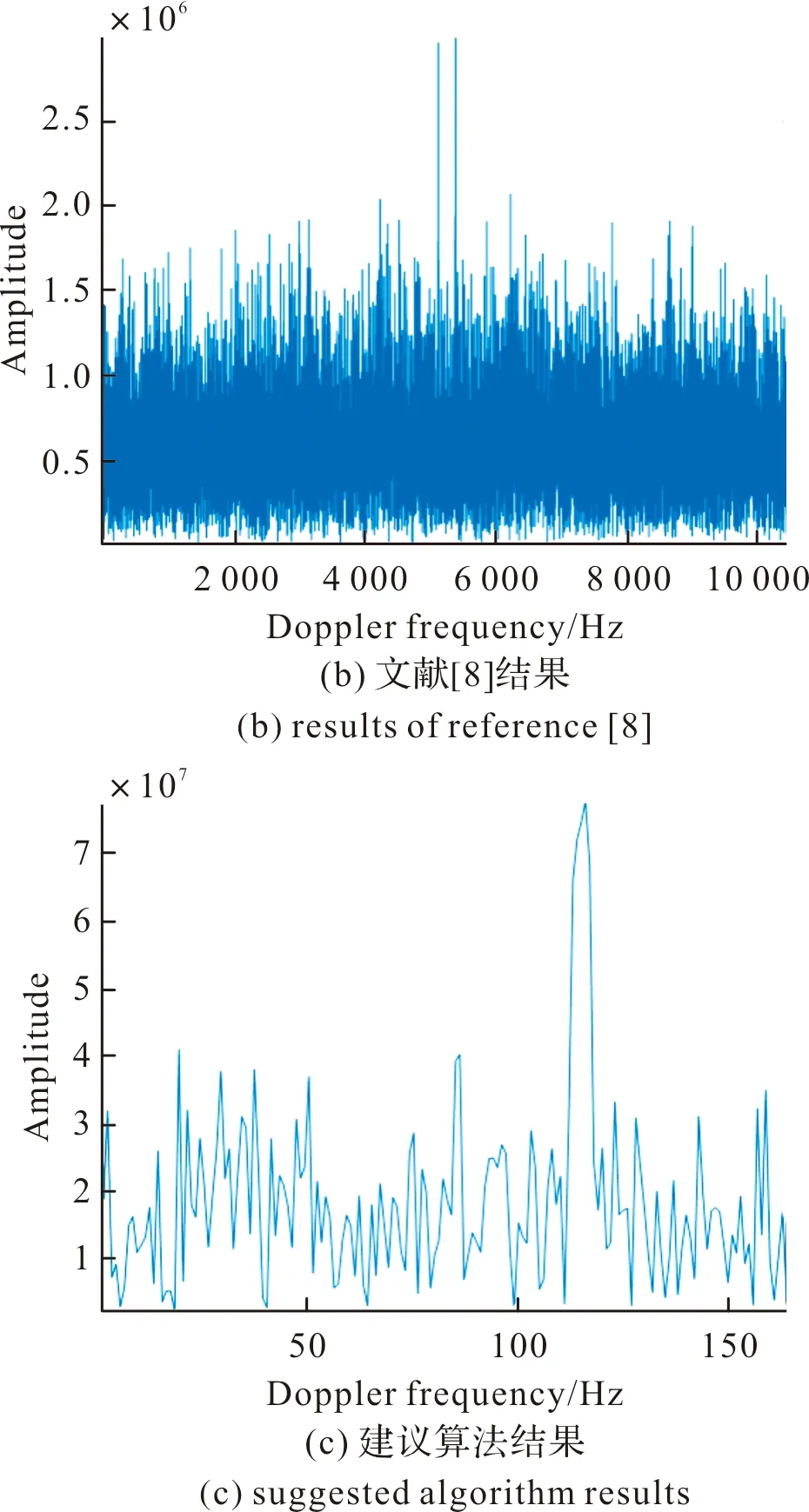
图7 弹丸数据不同算法结果Fig.7 Different algorithm results for bullet data
6 结论
提出了一种低信噪比下,基于两维FFT和VD-DPT算法的LFM信号参数估计方法。该方法通过将一维长序列信号分解为两维信号,其中列信号长度远小于信号整个长度,这可降低Dechirp算法运算量,同时也方便后续系统实现并行运算,以进一步提高算法执行效率;另外,针对调频率未知时,提出了VD-DPT的调频率估计方法,该方法能在较低信噪比下,实现对调频率参数的初步估计。仿真结果表明所提方法在低信噪比下的参数估计性能以及复乘运量量较现有的DPT 、Dechirp等方法具有明显优势。所提方法也可推广应用于微弱信号长时间相参积累以及高加速目标雷达检测等系统。
