能效最优准则下无人机空中高度的优化算法
2023-07-14陈卡
陈 卡
(驻马店职业技术学院公共教学部,河南 驻马店 463000)
0 引言
因机动性好、易部署,无人机(unmanned aerial vehicle, UAV)已在森林防火、航拍和应急救援领域广泛使用[1-2]。在应急救援中,将UAV作为空中基站,能帮助灾区用户恢复通信。然而,由于UAV储能量有限,续航时间不长,在所有基于UAV的应用中,空中通信系统(aerial communication system, ACS)的效率严重依赖UAV的能量效率[3-5]。
相比于传统的蜂窝通信系统,ACS系统对总体能量效率要求更高。原因在于:在ACS系统中,除了通信相关的能量消耗外,UAV在垂直爬升和悬停阶段均消耗能量。然而,现存的文献大部分只考虑了通信相关的能耗,而没有充分考虑UAV的能量消耗。
由于通信能耗量占UAV总的能量消耗量的比例很小,现存的能效优化算法实际上并不能获取ACS系统中的全局能效(global energy efficiency, GEE)的最优解。当UAV在空中接入点(aerial access point, AAP)的高度增加,它的视距覆盖区域也随之增加,但视距信道增益随之下降,消耗的能量也增加。基于这些事实,需对GEE进行重新定义。即通过在传输的数据量与所消耗的能量间进行权衡,计算AAP最优的悬停高度。
目前已有的部分研究工作[6-8]考虑了UAV在垂直爬升和悬停阶段消耗的能量。文献[6]通过联合优化移动轨迹以及在固定高度中的速度和加速度,最大化能量效率。文献[7-8]通过优化UAV的移动轨迹,最小化固定和旋转翼的能量消耗。
然而,上述工作在最大化GEE时并没有优化UAV的高度。为此,文中提出能效最优准则下无人机空中高度的优化算法(optimal energy efficient based aerial altitude optimization, EEAO)。EEAO算法在定义能效时,不仅考虑UAV的通信能耗,还考虑了UAV在爬升和悬停阶段的能耗。性能分析表明,综合考虑这些能耗可提升ACS系统的GEE。
1 系统模型
考虑正交多址接入下行广播传输场景,AAP作为移动基站。AAP覆盖区域内的用户所分配的带宽固定。假定系统内存在足够的正交信道。令Aue表示一个AAP所覆盖的区域面积,且Aue=πr2,其中r表示覆盖区域面积的半径,如图1所示。从图1可知,AAP在不同高度所覆盖的区域面积并不相同,高度h越高,覆盖区域面积越大。
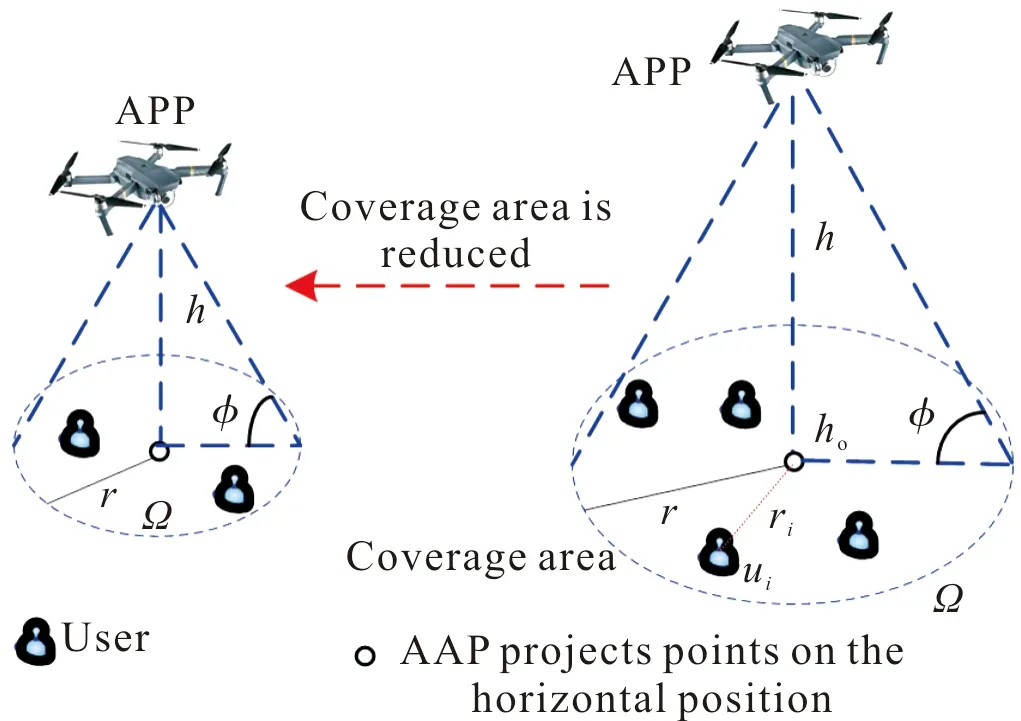
图1 网络模型Fig.1 Network model
在AAP覆盖的区域内有N个用户,用户密度ρue=N/Aue。图中φ表示维持AAP与用户间视距链路的最小倾斜角[9]。倾角φ、高度h和覆盖区域半径r满足关系:r=hcotφ。
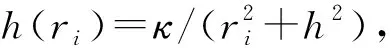
若用户ui位于覆盖区域边缘(ri=r),其能够获取的信噪比γr(signal-to-noise ratio, SNR)[10]为:
(1)
式中:PT表示AAP总的传输功率;σ2表示用户端的高斯白噪声变量的方差。
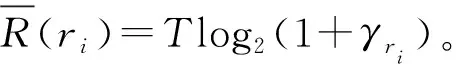

2 ACS系统的GEE及目标函数
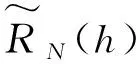
(2)
2.1 计算
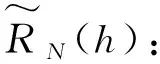
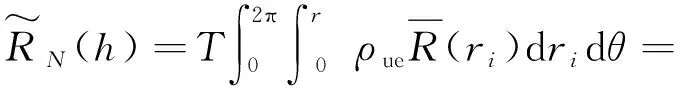
(3)
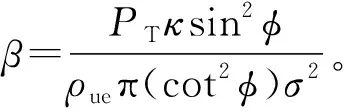
2.2 计算EAAP(h)
AAP的总体能耗由两部分组成:1)通信能耗,即因传输数据所消耗的能量;2) 在垂直爬升和悬停阶段所消耗的能量。令EC(T)表示AAP在时间T内的通信能耗;令E(h,T)表示AAP在时间T内垂直爬升和悬停阶段所消耗的能量。因此,EAPP(h)可表示为[13]:
EAAP(h)=EC(T)+E(h,T)=EC(T)+Ecl(h)+Eho(h,T)
(4)
式中:EC(T)=(PT+PH)T,PH表示AAP在传输数据时硬件电路所消耗的功率;Ecl(h)表示垂直爬升消耗的能量;Eho(h,T)表示盘旋时旋翼所消耗的能量。
依据文献[13],无人机在垂直爬升所消耗的能量为[13]:
Ecl(h)=αclh+βcl
(5)
无人机在高度为h的位置时,它盘旋T时间内所消耗的能量[13]:
Eho(h,T)=(αhoh+βho)T
(6)
式中:αcl,βcl和αho,βho均为无人机硬件参数。在第5节的仿真实验中,它们分别取值为αcl=315,βcl=-211.261和αho=4.917,βho=275.204。图2给出无人机在T=400 s时E(h,T)随高度h的变化情况。从图可知,E(h,T)随高度h呈线性增加。原因在于:飞行高度越高,空气温度和压强越低,这就使得无人机需要消耗更多的能量。
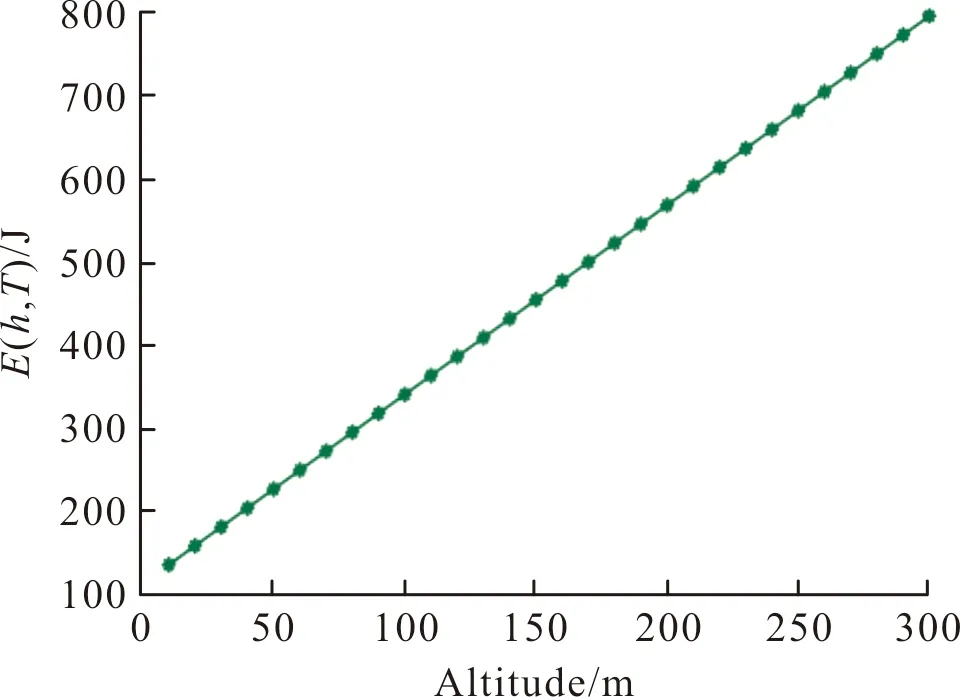
图2 E(h,T)随高度的变化情况Fig.2 The impact of altitude on E(h,T)
2.3 目标函数
EEAO算法旨在满足最小速率和高度约束条件下,通过优化无人机的高度,最大化网络的GEE值。为此,建立如P1所示的目标函数:
(7a)
s.t.hmin≤h≤hmax
(7b)
(7c)
式中:R0表示所需的最低速率。
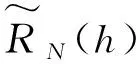
3 基于SCP的P1问题求解
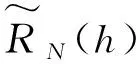
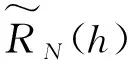
(8)
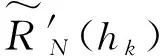
(9)
同理,利用Taylor近似法对式(7c)进行处理[16]:
(10)
因此,P1问题可重新表述为:
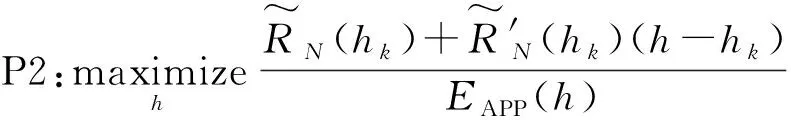
(11)
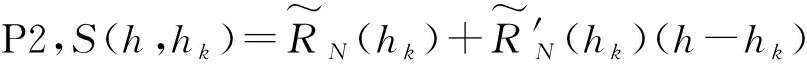
4 基于MFP的P1问题求解
利用SCP求解P1问题所得的解,并非是全局最优解。为此,利用MFP法求解P1问题。依据MFP算法的定义[18],若优化问题满足P3的规范形式,则可利用MFP求解[18]。
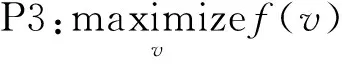
(12)
式中:f(v)是关于v的增函数;G⊂[0,a]是内部非空的紧法向量集;H是在[0,a]上的闭合集。
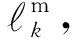
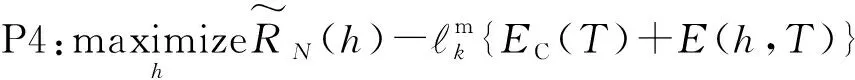
(13)
由于P4所示的优化问题并不符合P3定义的规范形式,为此需对P4进行形式转换处理。
先引入变量hmax,且hmax=[β/(2R0/W-1)]1/4。
再将式(13)重写为[16]:
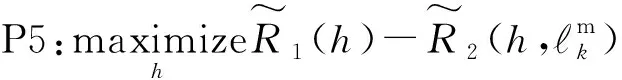
(14)
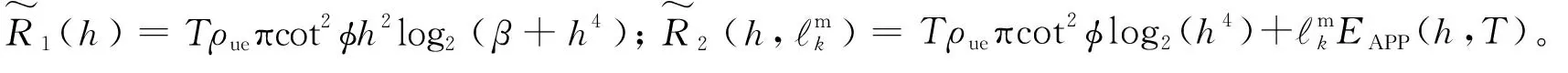
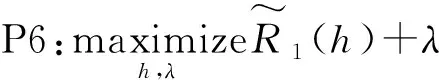
(15)
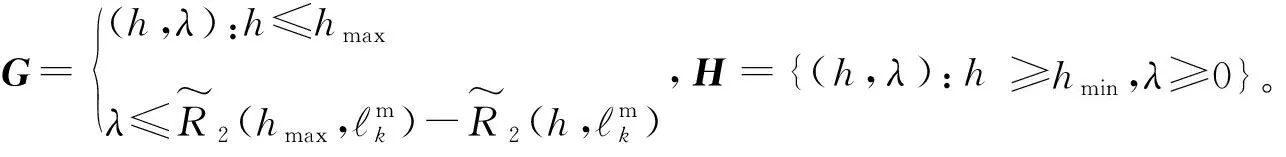
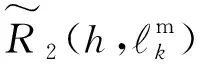
5 性能分析
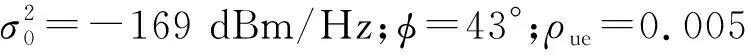
5.1 GEE性能
首先,分析SCP和MFP算法所获取的GEE性能,图3给出SCP和MFP算法的GEE归一化值随h的变化情况。
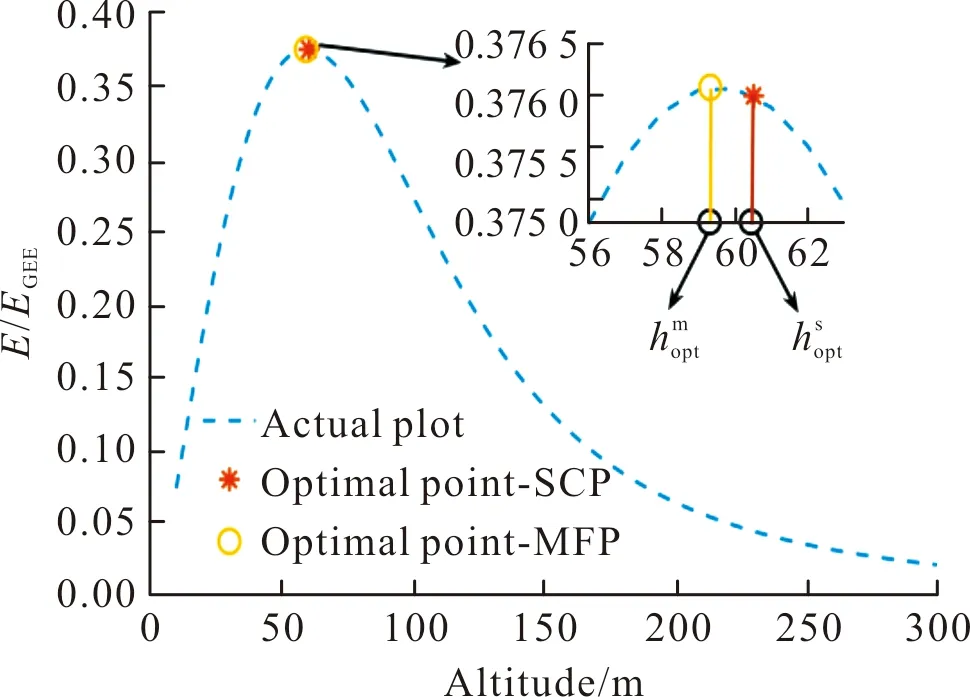
图3 归一化GEE随高度h的变化情况Fig.3 The impact of altitude h on normal GEE
从图3可知,在h较低或者在h较高区间,归一化GEE值较小。原因在于:在h较低时,AAP覆盖的用户数N=ρueπh2cot2φ随h的减少而下降,这就导致传输的总数据量减少,最终导致归一化GEE下降。在h处于较高区域时,用户与AAP间的信道增益下降,AAP覆盖的用户数增加,最终使EAPP(h)增加。此外,由于覆盖区域内用户数量的增加,分配至单个用户的功率就下降,这就降低了用户与AAP间信道增益。
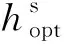
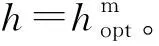
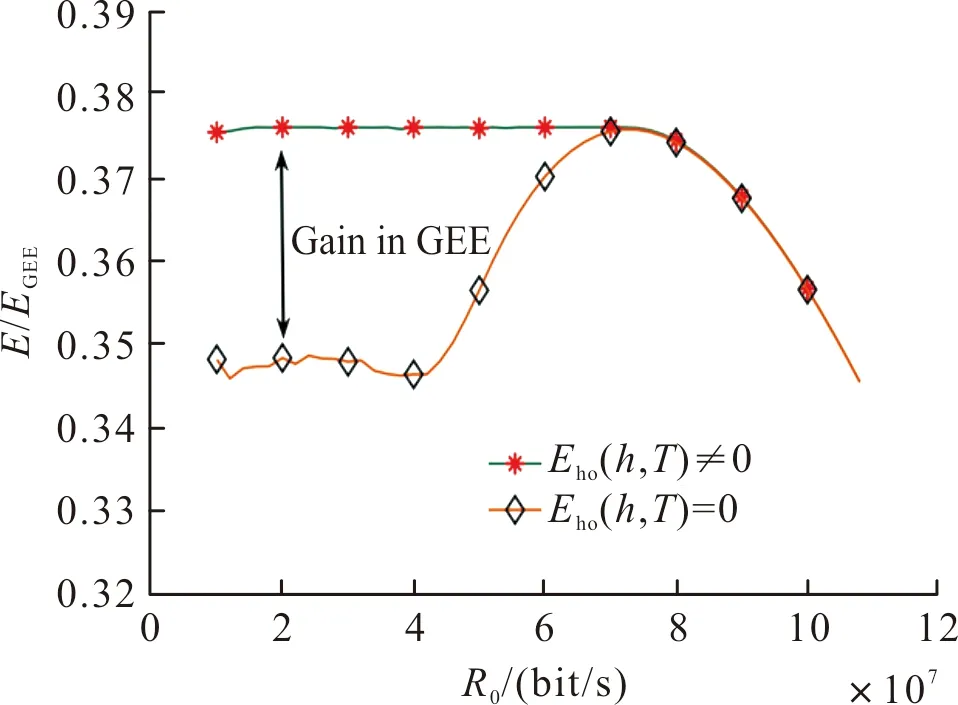
图4 归一化GEE随最小速率R0的变化情况Fig.4 The impact of R0 on normal GEE
图中考虑了Eho(h,T)=0和Eho(h,T)≠0两种情况。从图可知,Eho(h,T)≠0的GEE高于Eho(h,T)=0时对应值,这说明:在优化无人机高度时考虑旋翼能量消耗可以提高ACS系统的GEE。从侧面反映文中工作的意义。此外,在R0逐步增加的一段范围内,GEE随其变化甚小。随后,GEE随R0的增加而下降。
5.2 SCP法和MFP法迭代性能
图5给出SCP法和MFP法的迭代性能。图5的左侧的纵轴表示MFP的f(v)收敛值随迭代次数的变化情况。从图可知,当迭代次数达到1 200时,上限值接近下限值。
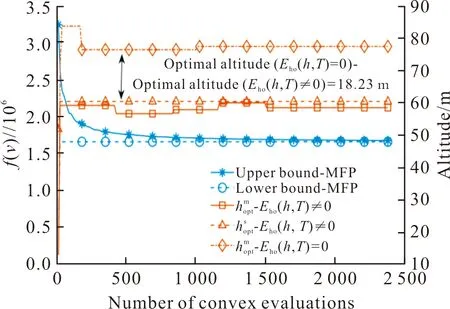
图5 SCP法和MFP法迭代性能Fig.5 Iteration performance of SCP and MFP
6 总结
为有效地提升ACS系统的能效,分析了UAV的高度对能效的影响,并提出基于能效最优准则下无人机空中高度的优化算法EEAO。EEAO算法先建立能效最大化的目标函数,再分别利用局部最优和全局最优算法求解,得到UAV最优的悬停高度。性能分析表明,在评估ACS系统的能效时,考虑UAV在垂直爬升和悬停阶段的能耗可提升系统能效值。
在分析ACS系统能效时,假定给每个用户分配的带宽是固定的。后期,将依据用户与UAV间信道增益情况,合理分配功率。即在评估系统能效时,考虑用户功率的分配问题,这将是后期的研究工作。
