基于靶标的火箭炮位姿视觉测量方法研究
2023-07-14杨长浩葛世程李学霖高光民李永泽冯高鹏
梁 熙,杨长浩,葛世程,李学霖,高光民,李 军,李永泽,冯高鹏
(1 中国工程物理研究院总体工程研究所,四川 绵阳 621999;2 中国运载火箭技术研究院北京航天计量测试技术研究所,北京 100076;3 南京理工大学机械工程学院,江苏 南京 210094)
0 引言
箱式火箭炮采用弹药箱式技术实现了多弹种的共平台发射。由于发射箱的质量大,通常其转运、吊装和装填是依靠弹药装填车的装填机构实现的[1]。在采用绳索和吊带吊装时,装填过程需要借助于人工辅助,装填效率低。为了解决该问题,目前多采用刚柔结合装填机构实现发射箱与地面、发射箱与弹药运输车、火箭炮与弹药运输车之间的快速自动装填,但实现快速自动对接,装填系统需要知道火箭炮与装填车的相对位置姿态信息,用于计算装填机构的运动参数[2]。火箭炮和弹药装填车之间的位置姿态包括相互之间的距离和角度。具体来说,停车点位可以造成两车之间的相对距离和角度,地面不平或者存在坡度是引起相对角度的重大因素。
视觉位姿测量技术具有实时、非接触测量以及自动化程度高等优点,适用于现场实时测量。目前,对使用靶标进行视觉位姿测量方法的研究较为广泛和成熟,主要集中在靶标设计、特征提取、位姿解算方法、位姿解算误差等方面[3-10]。文中使用视觉位姿测量方法不仅可以得到装填车与火箭炮车之间的精确位姿关系,并且采用具有准确位置的特征点的特征标志作为靶标,这种特征标志具有特征点提取简单、精度高等优点。
根据位姿视觉测量的要求,特征标志需要具有特征点易于检测识别和特征点的排序结果准确且唯一。黑白棋盘格在位姿视觉测量中使用广泛,但是它在相对偏转角度较大时会导致检测得到的特征点排序混乱,无法用于位姿视觉测量求解[11-12]。因此,一种可靠并且自动的角点识别与排序方法成为实现全自动位姿视觉测量方法的关键。
国内外科研人员对经典黑白棋盘进行了改进,文献[13]通过在黑白棋盘中增加沙漏状图形来减小由图像几何形状变化带来的影响;文献[14]设计了一种以渐进圆形为特征的平面标定模板。但是当这些标定模板图像相对相机光轴的旋转角度过大时,上述方法检测得到的特征点依然会出现排序混乱的情况。
文中提出了一种基于新型特征标志的视觉位姿测量方法。通过在经典黑白棋盘格上添加标志圆形成一种新型特征标志,解决了黑白棋盘格在大角度偏转下特征点排序混乱且不唯一的问题,然后设计了标志圆检测算法以及在Harris角点检测算法的基础上利用角点检测模板去除非棋盘格角点的特征点提取算法,并且根据特征标志上特征点的分布规律设计特征点的排序算法,实现了特征点的自动识别与排序。
在视觉位姿测量的过程中,通常假设起落架是刚体,因此只需要一个特征标志就可以得到起落架的位置与姿态。但在实际情况中,火箭炮起落架并非理想刚体,会在重力的作用下产生微小的弹性变形,因此需要分析这一微小变形对位姿测量的精度的影响。文中使用有限元方法得到起落架在不同载荷下的变形情况,进而得到其对位姿测量造成的误差大小。为了减小起落架变形带来的误差的干扰,需要根据其变形情况寻找一个减小变形干扰最合适的位置安装特征标志。
1 特征标志设计与识别
1.1 特征标志设计
设计的新型特征标志如图1所示,它由一个黑色标志圆和一个6×8的黑白棋盘格所组成。黑色标志圆的圆心作为整个特征标志的定位点和排序时的原点,黑白棋盘格内部的角点作为整个特征标志的特征点。经典棋盘格的角点分布具有对称性,因此在棋盘格旋转时排序结果会产生变化。但是在新型特征标志中,定位点与特征点相互配合,破坏了原有角点分布的对称性,每个角点都与定位点有着唯一的位置关系,从而解决了因为角点分布对称性使得黑白棋盘格在大角度偏转下特征点排序混乱出错的问题。同时,标志圆在特征标志发生偏转时,其在图像平面的投影是椭圆,椭圆的椭度和轴向可以辅助进行位姿测量,提升位姿测量的精度。

图1 新型特征标志Fig.1 New feature mark
1.2 特征点提取
1.2.1 椭圆检测
使用基于边界聚类的椭圆检测方法从边界图提取圆弧,再经过滤、聚类,最终用最小二乘法拟合出椭圆[15-16]。图2为基于边缘聚类的椭圆检测过程示例图。首先使用Canny边缘检测来检测图中的各个边界点,将边界点连接起来形成细小的边界列。然后进行线段拟合,即用折线代替原来的圆弧。使所有线段列的旋转方向保持统一,再根据曲率和凸性分割出椭圆弧段。得到椭圆弧段后还需要进行圆弧聚类,即将属于同一椭圆但是分开的两条或多条椭圆弧进行聚类[16]。使用最小二乘法进行椭圆拟合得到候选椭圆,对候选椭圆进行质量验证,剔除质量不高的椭圆,最终得到符合要求的椭圆。
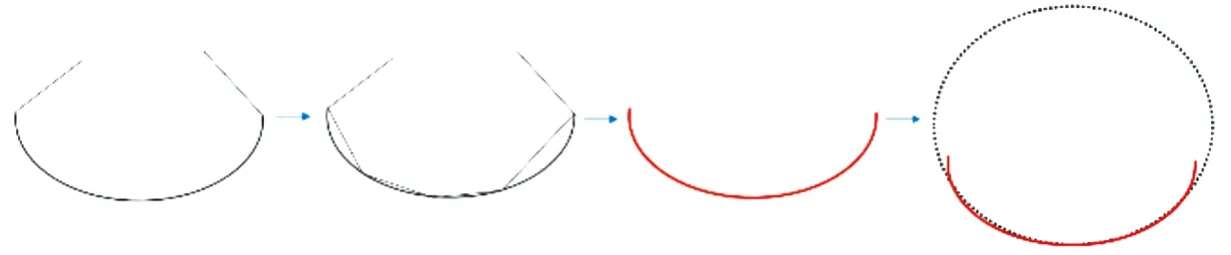
图2 基于边界聚类的椭圆检测过程示例图Fig.2 Example diagram of ellipse detection process based on boundary clustering
1.2.2 角点初定位
使用Harris角点检测算法检测棋盘格角点。但使用Harris角点检测算法检测角点时经常会检测到多个非棋盘格角点。为了去除这些非棋盘格角点,文中参考Geiger等提出的基于生长的棋盘格角点检测方法[17]在Harris角点检测算法的基础上做出了改进。
在实际情况中,棋盘格存在平移、偏转等情况,为此建立了两套检测模板用以检测棋盘格角点,这两套角点检测模板如图3所示。

图3 棋盘格角点检测模板Fig.3 Checkerboard corner detection template
图3中图(a)~图(d)适用于与坐标轴平行的棋盘格原型,图(e)~图(h)适用于与坐标轴成45°角的棋盘格原型。根据这两套角点检测模板可以计算出像素点与角点的相似程度,由此建立一个相应的角点响应函数C,该函数定义如下:
(1)
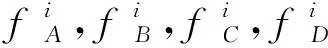
由角点响应函数C的定义可知,当4个卷积核中任何一个的响应值比较小时,C的值就会很小,因此,根据设定的阈值可以将非棋盘格角点滤除。
1.2.3 亚像素级角点定位
以上算法得到的棋盘格角点坐标的坐标值都是整数,但是实际上棋盘格角点的坐标通常不是整数,而是在整数值像素点的附近。因此,为了得到更精确的角点定位,需要进行亚像素级角点定位[18]。假设c点是理想的棋盘格角点位置,p点则是c点的邻域内的一个像素点,gp是p点的图像灰度梯度矩阵,则亚像素级的棋盘格角点坐标位置为:
(2)
1.3 特征点排序
检测出黑色标志圆圆心和黑白棋盘格的角点后,需要按照其分布规律设计排序规则以便实现特征点的自动排序。规定特征标志上的特征点的排列顺序如图4所示。根据特征点的排列规则,可以得到特征点的排序方法:

图4 特征点的排列顺序规定Fig.4 Arrangement order of feature points
1)以黑色标志圆的圆心作为排序时的原点,由它与另外7个特征点组成的一条直线就是新型特征标志最上面一行即第1行所在直线,这些特征点按照与原点的距离由短到长依次设为1号、6号、11号、16号、21号、26号、31号。
2)拥有5个特征点而且与第1行所在直线垂直的直线所在行即是棋盘格的各列,并按照与第1行交点的不同分别设为第1列~第7列。
3)对每一列上的特征点按照其到本列与第1行的交点的距离进行排序,其序号如图4所示。
2 起落架变形对测量精度影响分析
通过特征标志的位姿参数可以得到起落架相对于装填车的位姿参数,但是实际上火箭炮起落架有微小的弹性变形,文中使用有限元方法得到起落架在不同载荷下的变形情况,进而分析它们对位姿测量精度造成的影响。火箭炮起落架的有限元模型如图5所示。根据起落架上可能存在的不同载荷分布情况,可以得到起落架有限元分析的3种工况:空载工况、偏载工况、满载工况。其中空载工况下起落架上不放置发射箱;偏载工况下起落架左侧放置发射箱(含4发弹),右侧不放置发射箱;满载工况下起落架上放置两箱发射箱(共含8发弹)。通过有限元分析得到火箭炮起落架在不同工况下的弹性变形情况后,进而根据起落架的变形位移分析其对测量精度的影响。
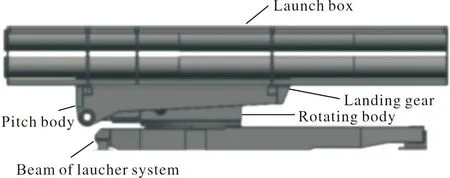
图5 箱式火箭炮起落架模型图Fig.5 Model diagram of landing gear of box rocket launcher
空载工况下铅垂方向位移云图如图6所示,空载时的起落架最大变形位移为-0.47 mm,最小变形位移为-0.26 mm。
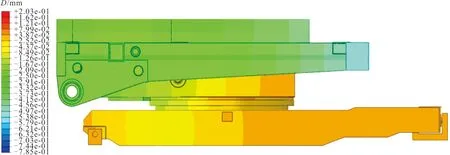
图6 空载工况下铅垂方向位移云图Fig.6 Displacement cloud diagram in the vertical direction under no-load conditions
满载工况下铅垂方向位移云图如图7所示,满载时的起落架最大变形位移为-13.75 mm,最小变形位移为1.53 mm。
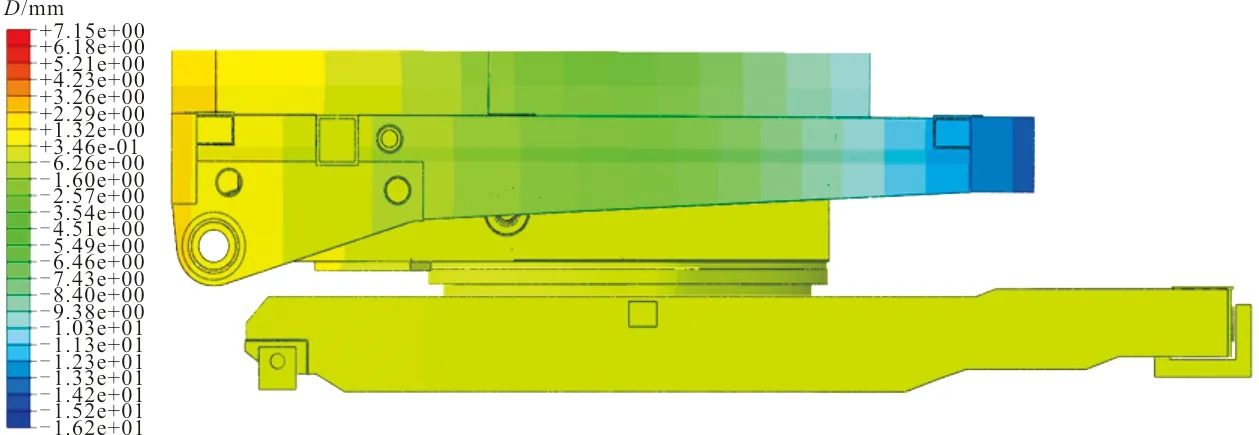
图7 满载工况下铅垂方向位移云图Fig.7 Displacement cloud diagram in the vertical direction under full load conditions
偏载工况下铅垂方向位移云图如图8所示,偏载时起落架左侧最大变形位移为-9.74 mm,最小变形位移为-0.57 mm。偏载时起落架右侧最大变形位移为-5.19 mm,最小变形位移为1.80 mm。
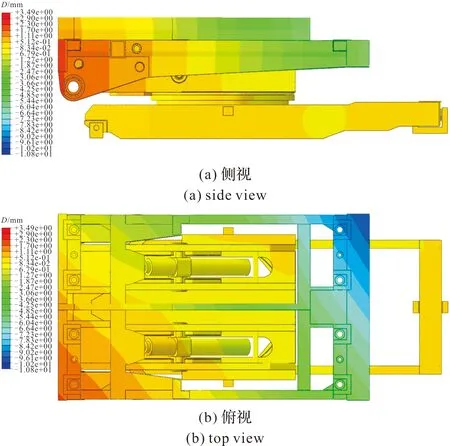
图8 偏载工况下侧视铅垂方向位移云图Fig.8 Displacement cloud diagram in the vertical direction from side view under eccentric load conditions
根据起落架变形数据,可以计算得到起落架变形引起的角度变化如下:空载时产生的角度变化为0.003°,满载时产生的角度变化为0.21°,偏载时产生的角度变化为0.13°。视觉位姿测量方法整体角度误差均值为0.22°,与视觉位姿测量算法的误差相比较,起落架变形产生的角度变化较小并在视觉位姿测量方法的角度误差范围内。因此可以认为起落架变形对位姿测量的结果造成的影响较小。
为进一步减小起落架变形带来的误差干扰,根据其变形情况寻找一个变形干扰最小的位置安装特征标志。根据起落架的变形情况,将特征标志的安装位置初步设置在起落架的中部区域。基于满载时起落架右侧的弹性变形位移曲线与偏载时起落架左右两侧的弹性变形位移曲线十分近似,因此通过满载状态下的起落架右侧的弹性变形位移曲线寻找最佳安装位置。
从起落架后端到前端依次间隔一定距离取点,根据这些点(sercial No.,SN)在起落架上的不同分布位置,可以将这些点分为两部分并分别进行直线拟合。从起落架后端开始的SN1~SN23点得到的拟合直线如图9(a)所示,SN23~SN44点得到的拟合直线如图9(b)所示。
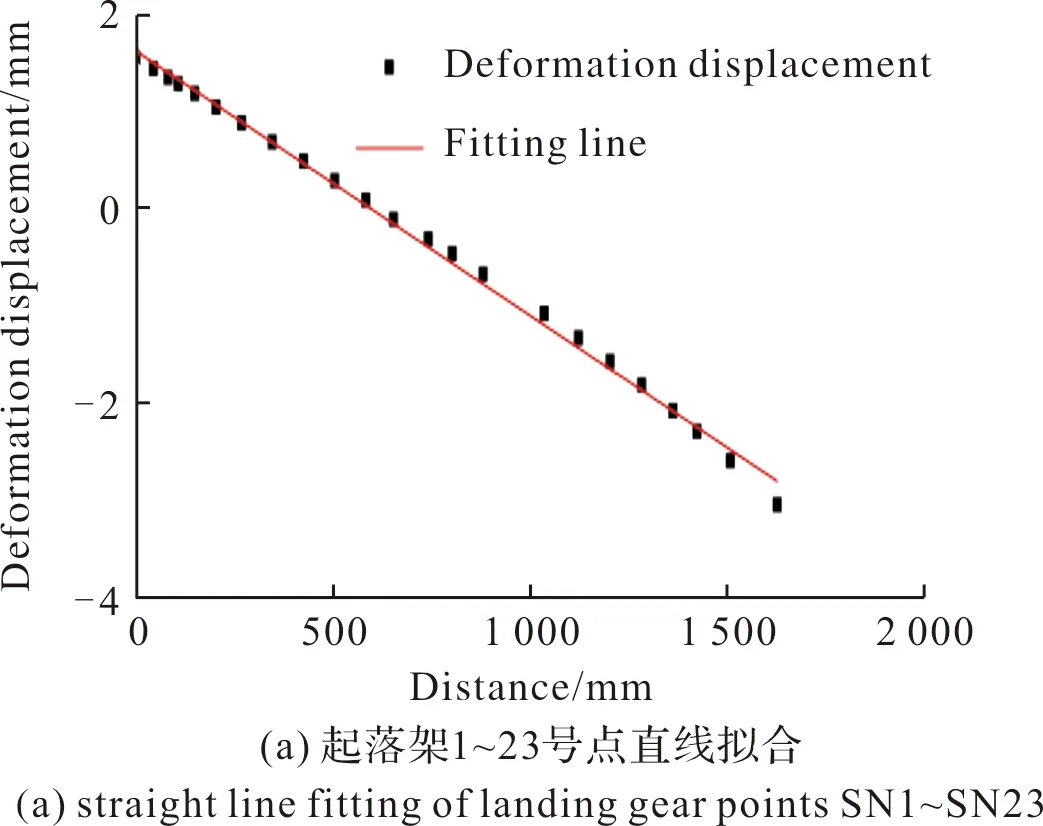
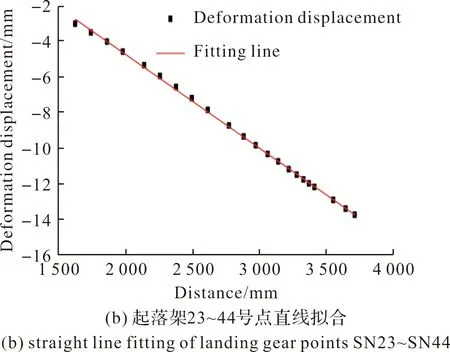
图9 满载状态下火箭炮起落架不同部分的拟合直线Fig.9 Fitting straight lines of different parts of rocket landing gear under full load
对满载状态下的火箭炮起落架中部、后部取到的第1号~第23号点进行直线拟合,得到的拟合直线的函数表达式为:
y=-0.00271x+1.6088
(3)
对满载状态下的火箭炮起落架前部、中部取到的第23号~第44号点进行直线拟合,得到的拟合直线的函数表达式为:
y=-0.00255x+5.76792
(4)
两条拟合直线的交点坐标为(1 631.03 mm,-2.81 mm),说明距离火箭炮起落架后端1 631.03 mm处即为火箭炮起落架前后两部分弹性变形区域的交界处。取这一区域为最佳的特征标志安装与观测位置。为简单方便,将文中寻找的最佳特征标志安装与观测位置与火箭炮起落架后端之间的距离取整设置为1 630 mm。
综上所述,文中设置两个观测点并且分别将这两个观测点设置在火箭炮起落架左右两侧距离后端1 630 mm处。在此位置可以很方便地由观测点处特征标志的位置与姿态信息和起落架变形规律推导出起落架上锁紧孔的位置与姿态信息。
火箭炮起落架上特征标志的安装位置如图10所示,图中特征标志上的小红点为靶标坐标系原点,也就是棋盘格左上方的第一个角点。
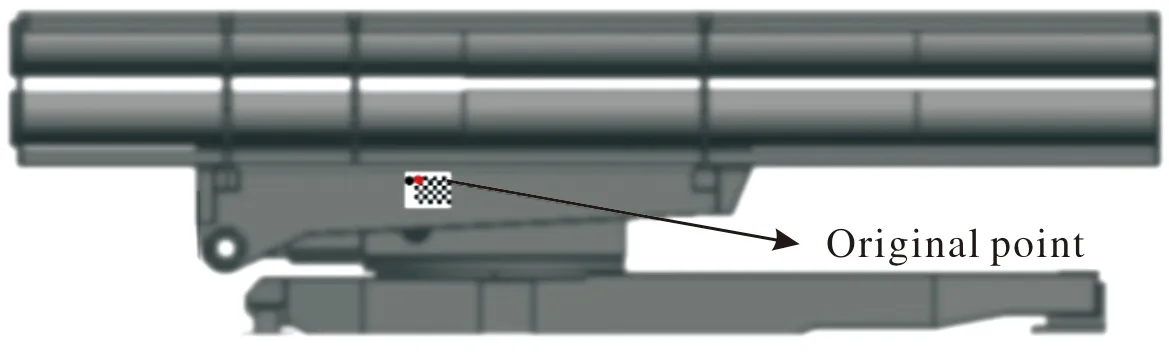
图10 火箭炮起落架上特征标志安装位置Fig.10 Installation position of feature mark on rocket landing gear
3 实验检验
3.1 算法精度实验
位姿测量实验需要将经过标定的相机固定并保持相机参数不变,然后将靶标放置在相机前方3 000 mm处拍照,位姿测量实验的场景示意图如图11所示。
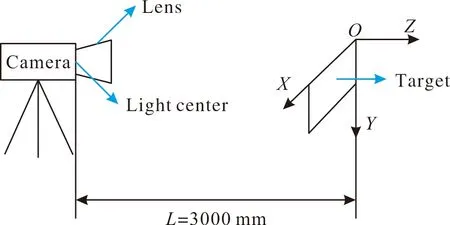
图11 实验装置与场景示意图Fig.11 Experimental device and scene diagram
使用MATLAB相机标定工具箱标定相机后处理靶标照片,靶标照片的重投影平均误差为0.47 mm,满足使用要求,标定值可以接受。使用文中算法处理靶标照片,得到靶标照片的位置与姿态参数。将算法得到的位姿参数与标定值进行做差,然后将偏差值按照序号依次显示在图上。如图12所示,分别为各序号点(SN)位姿参数的偏差值。
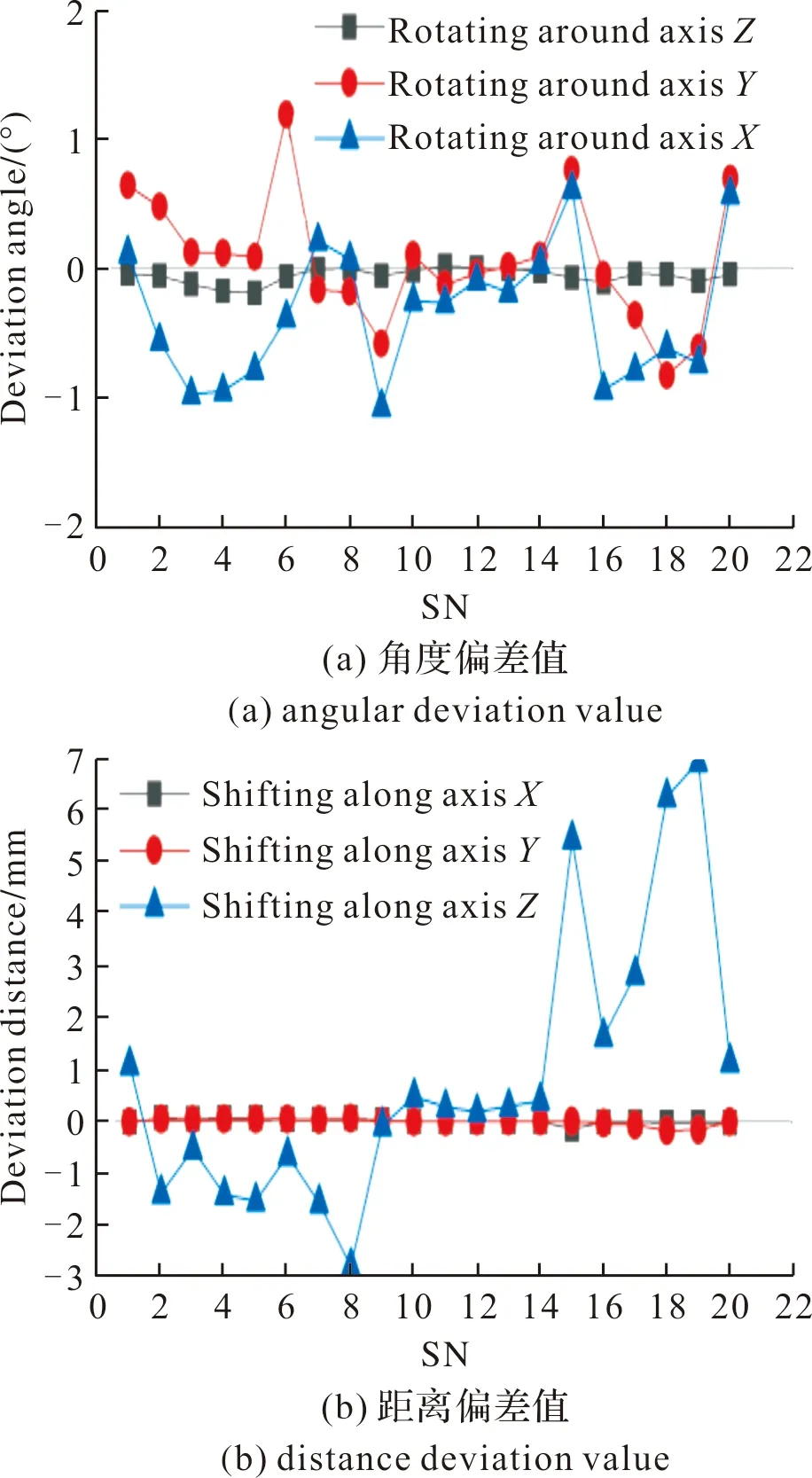
图12 各位姿参数偏差值Fig.12 Attitude parameter deviation
位姿测量算法的角度误差均值为0.16°,在X轴、Y轴上位移误差均值为0.01 mm,在Z轴上位移误差均值为0.85 mm。根据使用新型吊装机构吊运储运发射箱对起落架位置与姿态的测量精度要求:角度精度为1°,位置精度为2 mm,由于算法的误差比较小而且在允许范围之内,因此可以认为该算法的精度满足测量精度要求。
3.2 模板旋转实验
为验证设计的靶标在大角度旋转下的排序不变性以及排序算法的稳定性和精准性,将靶标放置在相机前方3 000 mm处,拍摄靶标无旋转和分别绕Z轴、Y轴、X轴旋转45°的典型旋转场景的照片。靶标照片经过处理后得到的标志圆及其圆心和棋盘格角点如图13所示。

图13 不同姿态靶标处理结果图Fig.13 Processing results of targets with different attitudes
如图14所示:靶标无旋转时绕Z轴旋转的角度误差均值为-1.05°;绕Y轴旋转的角度误差均值为0.63°;绕X轴的角度误差均值为-0.25°。
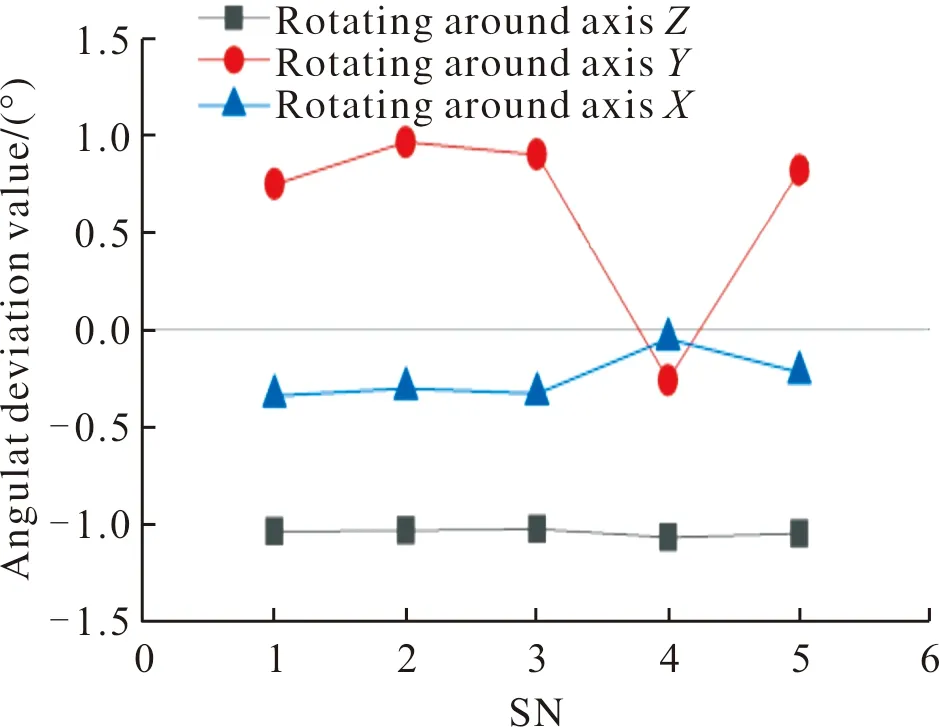
图14 靶标无旋转时角度偏差值Fig.14 Angular deviation value of target without rotation
如图15所示:靶标绕Z轴旋转45°时绕Z轴旋转的角度误差均值为-1.79°;绕Y轴旋转的角度误差均值为-0.10°;绕X轴的角度误差均值为-0.18°。
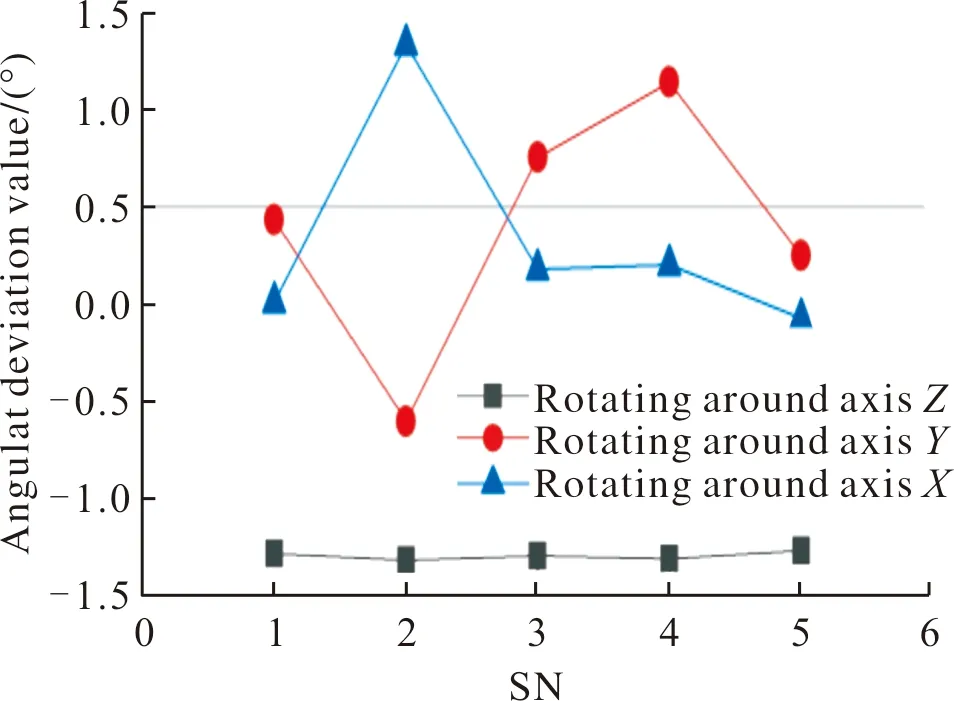
图15 靶标绕Z轴旋转45°时角度偏差值Fig.15 Angular deviation value when the target rotates 45° around axis Z
如图16所示:靶标绕Y轴旋转45°时绕Z轴旋转的角度误差均值为-1.07°;绕Y轴旋转的角度误差均值为-0.69°;绕X轴的角度误差均值为-0.32°。
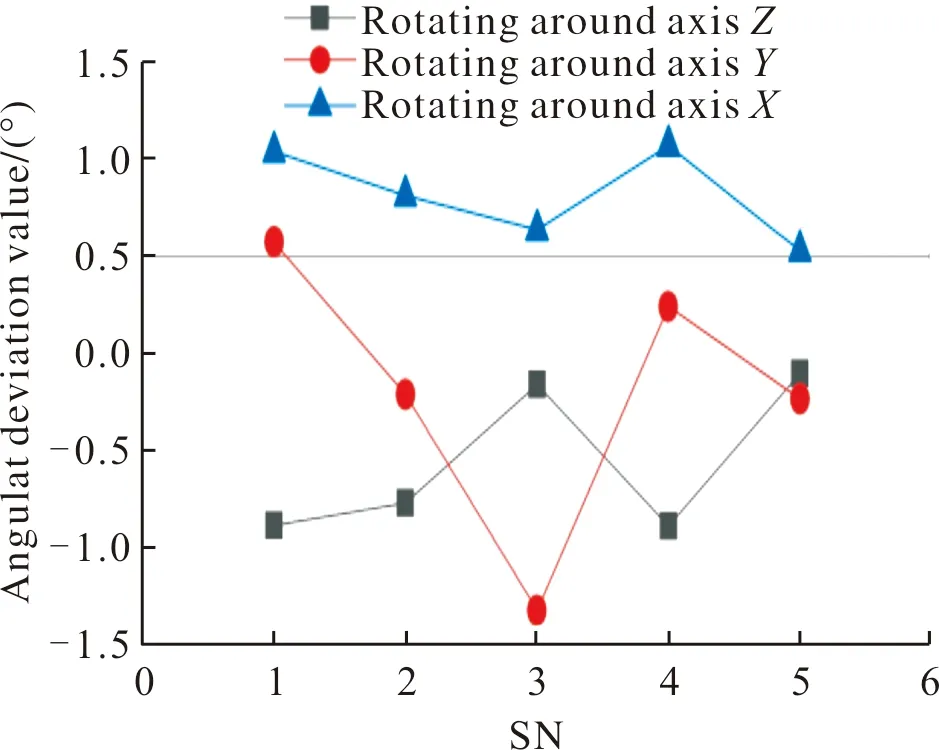
图16 靶标绕Y轴旋转45°时角度偏差值Fig.16 Angular deviation value when the target rotates 45° around axis Y
如图17所示:靶标绕X轴旋转45°时绕Z轴旋转的角度误差均值为-1.08°;绕Y轴旋转的角度误差均值为-0.11°;绕X轴的角度误差均值为0.32°。
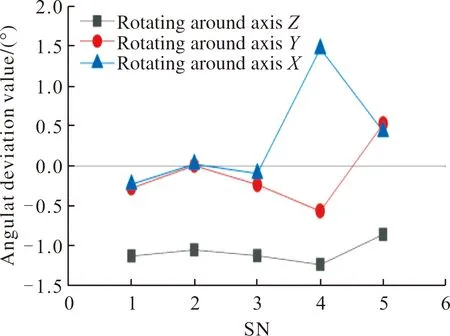
图17 靶标绕X轴旋转45°时角度偏差值Fig.17 Angular deviation value when the target rotates 45° around axis X
视觉位姿测量方法的角度误差均值为-0.55°,其中,绕Z轴旋转角度偏大,这是由于靶标与玻璃板存在一定的偏差造成的。视觉位姿测量方法在本次靶标旋转实验中的误差相比之前实验的误差较大,经过分析这是由于相机标定误差、靶标制作误差、靶标实际位姿测量误差等导致的。
综上所述,靶标在分别绕Z轴、Y轴、X轴各旋转45°时的典型旋转场景下具有排序不变性,而且位姿测量的精度满足要求。为了进一步验证文中靶标和算法的性能,控制靶标同时绕3个坐标轴旋转任意角度进行实验。靶标照片经过文中算法处理后解算得到的旋转角度数据以及它们相应的实际旋转角度数据依次按序号排列在表1中。
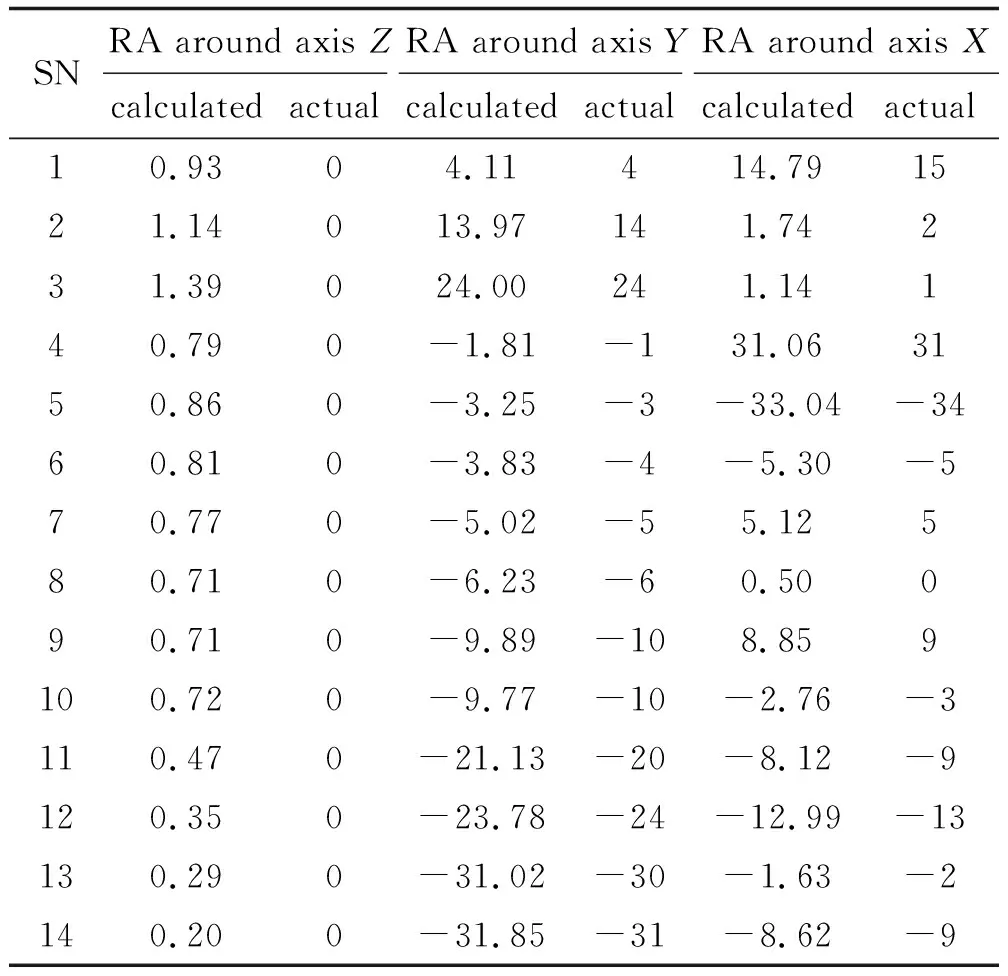
表1 各混合旋转靶标照片旋转角度解算值与实际值Table 1 The calculated and actual values of the rotating angle (RA) of each hybrid rotating target photo (°)
由表1可知:在靶标绕3个坐标轴进行任意旋转的情况下,依然能解算出正确的角度数据,这说明对处于不同旋转状态的靶标照片,排序算法均能得到准确且唯一的排序结果,验证了排序算法的稳定性和准确性。
如图18所示:视觉位姿测量方法在靶标同时绕3个坐标轴旋转任意角度时,绕Z轴旋转的角度误差均值为0.72°;绕Y轴旋转的角度误差均值为-0.25°;绕X轴的角度误差均值为0.19°;整体角度误差均值为0.22°。其中,靶标绕Z轴旋转的角度偏差较大,这是由于靶标与玻璃板存在一定的偏差造成的。
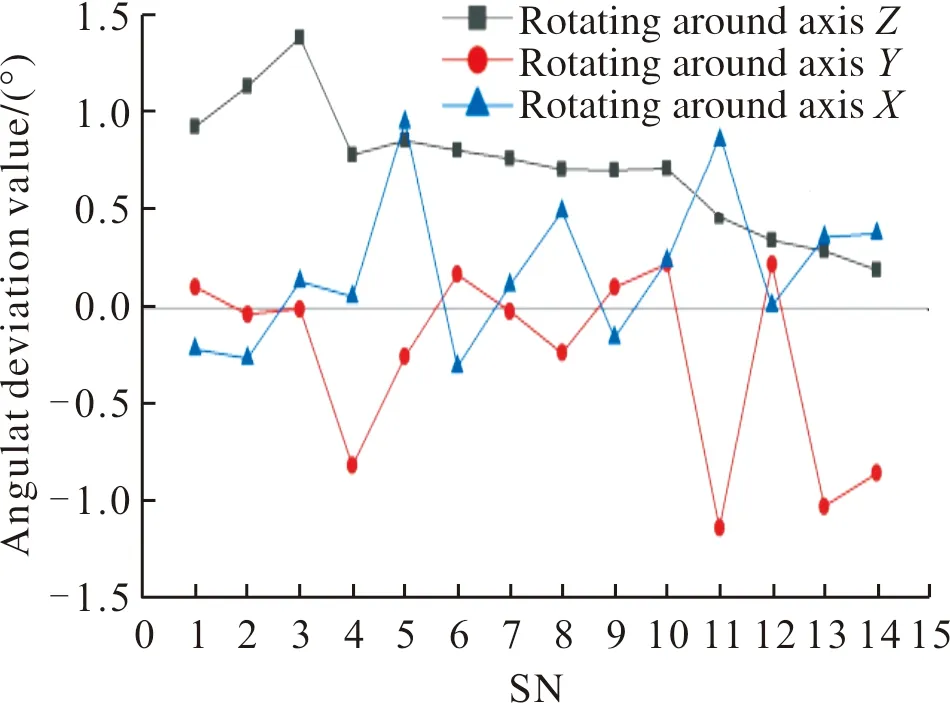
图18 混合旋转靶标旋转角度偏差值Fig.18 Rotation angle (RA) deviation of mixed rotating target
综上所述,设计的靶标在大角度旋转下的具有排序不变性,排序算法稳定精准,在靶标大角度旋转的情况下依然能够得到准确且唯一的排序结果,同时,文中视觉位姿测量方法的实际角度测量误差比较小,满足测量精度要求。
4 结论
经过对新设计的火箭炮位姿测量方法的系统研究,主要结论如下:
1)通过对黑白棋盘格的改进设计,提出了一种新型特征标志,实现了排序唯一性。
2)由椭圆检测算法、角点提取算法和特征点排序算法实现了特征点的自动检测和排序。
3)通过对起落架变形的有限元法分析得到最合适的特征标志安装位置,减小了起落架变形带来的误差干扰。
4)实验结果表明,文中视觉位姿测量方法的角度误差均值、位移误差均值分别为0.16°、0.29 mm,达到了测量精度要求。
