PBX炸药断裂行为仿真计算方法研究

袁洪魏,唐 维

(1.中国工程物理研究院 化工材料研究所,四川 绵阳 621900;2.中国工程物理研究院 研究生院,北京 100193)

引 言

高聚物黏结炸药(Polymer Bonded Explosive, PBX)作为先进武器的重要炸药,在武器杀伤、破坏与动力能源方面发挥着关键性作用。由于PBX材料强度较低[1],在制造、运输、服役过程中易受载荷刺激而产生裂纹,严重影响武器系统的安全性和可靠性[2]。作为武器装备安全性和可靠性评估的重要手段,数值预测PBX炸药在典型载荷下的裂纹起裂扩展规律具有重要意义。

PBX材料是由体积占比95%的含能晶体及少于5%的黏结剂高温压制而成,其力学特性具有显著的黏弹性、拉压不对称性、压力相关性以及温度相关性等[3]。其黏弹性表现在加载速率效应[4]、蠕变[5]及松弛等行为;拉压不对称性表现在其压缩强度远高于拉伸强度,且拉伸强度一般小于10MPa[1],因此在结构件中PBX材料常以拉伸失效为主。压力相关性表现在材料应力—应变响应与静水压力(围压)相关,静水压越大,则材料强度越高[6-8]。因此,PBX材料往往能承受长时压缩载荷,而在拉伸载荷作用下容易发生低应力短时失效。与此同时,由于PBX材料脆性特征明显(破坏应变较低[1]),在环境温度冲击[9]以及动态载荷[10]作用下易发生多裂纹并生且分叉融合等现象。为准确仿真PBX结构断裂行为,一方面需要充分考虑PBX材料的黏弹性、拉压不对称性及压力相关性等特殊力学性能,另一方面需要计算方法能进行多裂纹萌生、扩展、分叉和融合等复杂断裂行为的仿真计算。

针对PBX结构断裂行为仿真,首先从损伤力学和断裂力学两个角度分析了目前断裂计算方法的现状与困境,然后针对新兴的断裂相场法阐述了其基本思想、优势及在PBX炸药中应用的不足,接着针对相场法的不足提出了考虑拉压不对称性的黏弹性断裂相场计算方法,并通过多个实际算例展示了其对于PBX材料力学行为及结构裂纹行为仿真分析的优势与潜力。

1 现有断裂计算方法

从力学学科上区分,断裂行为的仿真分析方法一般可分为损伤力学和断裂力学两个分支。

1.1 损伤力学

损伤力学方面常采用含损伤本构模型的方式进行断裂行为仿真,即在本构模型中引入一个损伤因子,当损伤因子达到1时便认为失效,材料失效区域的连通便被认为是裂纹,所以该方法可以较为便利地进行裂纹的起裂、扩展、分叉和融合仿真分析。

罗景润[11]针对PBX拉伸力学行为建立了指数型损伤演化模型;李丹[12]采用唯象分析和细观统计相结合的方法提出了PBX材料的率型损伤本构模型;李英雷[13]、黄垂艺[14]基于损伤型Z-W-T模型研究了考虑PBX材料非线性黏弹性的本构关系,这些损伤本构模型大都致力于应变率效应及单轴应力—应变曲线的高精度描述上,尚未考虑PBX材料拉压不对称性、围压相关性等。

在所有的PBX材料损伤本构模型中,不可避免地需要讨论viscoSCRAM模型,该模型考虑了微裂纹、微孔洞等细观损伤机制,反映了炸药从变形到破坏的物理过程,能较好地描述简单应力状态下材料断裂破坏的特征。Dienes[15]首先提出了著名的统计微裂纹模型(SCRAM),后又进一步发展[16],SCRAM模型基于应变率可加性,包含一个描述基体行为的弹塑性部分,加上描述微裂纹网络(形核、长大和聚并)的各向异性损伤。Addessio和Johnson[17]对SCRAM模型进行了简化,提出了具有各向同性损伤和无微裂纹聚合的IsoSCRAM模型。Bennett[18-19]在IsoSCRAM模型的基础上附加黏弹性部分,从而提出了viscoSCRAM模型,该模型宏观上考虑了炸药的黏弹性,细观上以微裂纹作为主要损伤机制。柳明[20]对viscoSCRAM模型进行了修正,增加了Bodner-Partom黏塑性,引入压力相关拉伸损伤增强因子,使得模型可以较为准确地描述PBX材料的拉压不对称性。其他损伤本构模型大都采用类似思路进行模型构建[21]。

可以看出,目前损伤本构模型重点在于描述材料从损伤到失效的行为描述而非断裂行为本身的准确预测,同时现有的损伤本构模型尚不能完全同时考虑PBX材料的拉压不对称性和压力相关性;除此之外,基于损伤力学的仿真方法无法准确考虑裂纹尖端的应力奇异性,因此无法准确预测PBX结构的断裂过程。

1.2 断裂力学

目前基于断裂力学的PBX结构裂纹仿真方法主要分为基于有限元框架的数值计算方法以及非有限元框架的新型数值计算方法。

基于有限元方法的断裂数值方法主要包括界面单元法(CFEM)及扩展有限元法(XFEM)。界面单元法是在单元之间插入内聚力单元以模拟裂纹的起裂扩展,Tan H[22]和郭虎[23]均开展了界面单元法在准静态加载下PBX结构力学响应的应用研究,界面单元法虽然方法简单,但其只允许裂纹在网格边界上扩展,具有强烈的网络依耐性和计算不稳定性[24]。扩展有限元方法通过Enrich函数补充自由度,裂纹可在单元内部进行扩展,弥补了内聚力有限元法的不足。黄西成[25]、戴开达[26]、李生涛[27]等均采用XFEM对PBX材料在准静态或动态加载条件下的断裂过程开展了仿真研究,但是XFEM需要追踪裂纹面,处理过程复杂,且在模拟三维裂纹任意扩展时存在困难[28]。其他的单元删除法、广义有限元法、网格重构法等,大都存在需要追踪裂纹面、判据众多、难以处理三维问题等缺点。

在非有限元框架的新型裂纹计算方法方面,主要包括离散元法(DEM)、近场动力学方法(PD)、数值流形元法(NMM)。离散元法是一种无网格方法,其将固体离散为一系列带质量的物质点,通过求解物质点之间相互作用的动力学方程以开展裂纹仿真分析。傅华[29-30]采用DEM模拟了PBX细观尺度的动态加载试验,但是离散元方法假设较多,缺乏理论严密性,同时细观参数难以确定,计算收敛性较差[31]。近场动力学法是另一种无网格方法,通过用物质点之间的关系积分方程代替微分方程求解物质点的运动,以此仿真分析裂纹问题。李潘[32-34]建立起可应用于PBX材料的近场动力学模拟方法并应用于PBX试样的准静态破坏行为计算,但是PD计算效率低下,存在数值不稳定性,难以进行三维问题分析,且传统物性参数与PD模型参数转换困难[34]。数值流形元法是通过两套独立覆盖系统和截断不连续形函数将连续与不连续分析统一在一个框架内,其对于裂纹扩展模拟没有网格依赖性,易于处理复杂裂纹。北京理工大学陈鹏万团队[35-37]系统研究了基于数值流形元法的PBX材料宏细观破坏过程仿真计算方法,但是NMM存在计算效率低下、收敛性较差、难以处理三维情形的问题[35]。因此,新兴的裂纹数值计算方法由于均存在计算效率低下、难以计算复杂情形、宏观物性参数难以转换为仿真所需参数等问题,难以进行实际工程应用。

因此,现有的PBX结构断裂行为计算方法,其均存在固有的不足而不能既考虑PBX材料的力学特性又可以计算PBX结构的复杂断裂行为。

2 断裂相场法的优势与不足

断裂相场法(Phase Field Method to Fracture)自本世纪初诞生,便由于其理论完备且相对简单、数值实现方便、且易于计算复杂裂纹等优点,在近二十年得到了迅猛发展。

2.1 相场法的发展现状与优势

1998年,Francfort和Marigo[38]将裂纹表面能作为连续体势能的一部分,通过最小势能原理建立了断裂变分理论。随后Bourdin和Francfort[39]于2000年结合相场理论,通过引入序参量(后来称为相场标量),给出了断裂面的弥散表达式,为断裂相场模型的发展奠定了坚实的理论基础。断裂相场法的基本思想(以线弹性断裂系统为例)为:其自由能同时包含弹性能和裂纹表面能,裂纹的起裂、扩展、分叉和融合等行为受自由能最小化原理控制。因此该方法具有3方面的优势:其一,理论完备且简单,断裂相场法是Griffith断裂理论[40]的延伸,满足能量守恒定律,并且仅需要临界能量释放率GIC断裂判据,避免了传统断裂理论需要定义起裂、扩展、分叉等多个准则的缺陷;其二,数值实现方便,断裂相场法独立于数值处理方法,因此可以基于成熟的有限元框架进行程序开发,减少了方法实现的成本,易于推广应用[41];其三,易于处理复杂问题,断裂相场法中裂纹的萌生、扩展、融合、分叉等演化行为是一组耦合偏微分方程数值解的自然结果,均不需要额外处理,能方便地仿真各种复杂裂纹问题,避免了跟踪复杂的裂纹几何。

由于断裂相场法独特的优势,其自诞生便迅速发展。Miehe[42]成功模拟了I、II型裂纹在不同加载强度下裂纹的扩展长度和发展方向;Borden[43-44]针对动态加载下脆性材料断裂行为提出了相应的数值计算策略并实现了二维和三维动态裂纹扩展仿真模拟;Mesgarnejad[45]通过多种实验对不同脆性断裂模型进行了定性和定量对比。为了进一步满足压剪情况下的起裂扩展行为,清华大学柳占立[46]、同济大学Zhou等[47]基于Morh-Column失效准则修正了相场驱动能量项采用显式相场法实现了脆性材料动态及准静态压剪失效仿真模拟。目前断裂相场法在线弹性断裂方面已发展较为成熟,线弹性断裂相场理论系统如图1所示,同时在弹塑性分析[48]、力热耦合[49]、流固耦合(水力压裂方面)[50]、力电耦合等多场耦合领域[51],通过在自由能泛函中进一步引入塑性耗散能、热能等并结合相场变分理论开展了相场的扩展应用研究。

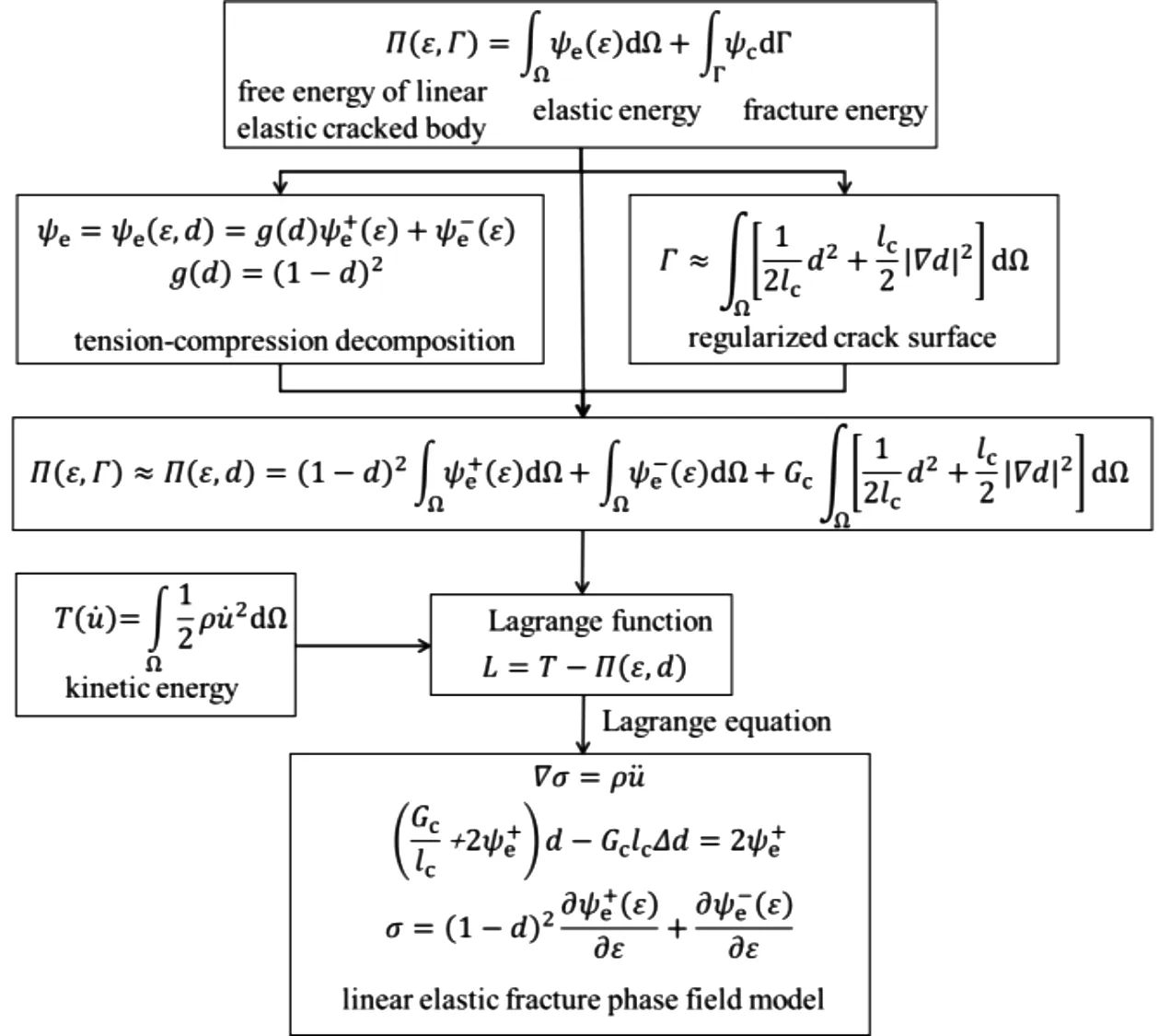
图1 线弹性断裂相场法理论Fig.1 Theory of the linear elastic fracture phase field method

2.2 线弹性相场法中的拉压不对称性

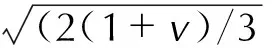
2.3 黏弹性相场法的现状与不足

自2018年来多位研究人员开展了黏弹性相场法研究。Liu[59]提出了线性黏弹性断裂相场方法,可以描述不同加载速率下的断裂行为,该方法以弹性能作为裂纹驱动力。Loew[60]将广义Maxwell黏弹性模型和Yeoh超弹性模型相结合,建立了橡胶材料的速率相关相场损伤模型。Yin和Kaliske[61]将橡胶材料的标准Maxwell黏弹性模型与Neo-Hooke超弹性模型相结合,建立了黏弹性断裂相场模型,其采用Maxwell模型中平衡分支和非平衡分支的弹性能作为裂纹驱动力。Shen[62]提出了基于黏性耗散能驱动裂纹演化的黏弹性断裂相场方法,不同于Loew[60],在该模型中,仅部分黏性耗散能驱动裂纹的演化,并研究了耗散能对蠕变、松弛、应变率效应和循环载荷作用下材料力学性能的影响。Huang[63]在Shen[62]的基础上针对PBX材料建立了细观断裂相场仿真分析模型。Dammaß[64]建立了统一的线性黏弹性断裂相场模型,其在Shen[62]的基础上考虑了体积变形和偏变形的黏弹性,并对弹性能和耗散能采用不同的退化函数。

值得注意的是,Liu[59]、Yin和Kaliske[61]以及Shen[62]均采用体积偏分分解法求得弹性能的拉伸分量和压缩分量,其主要原因是黏弹性本构模型通常分解为体积部分和偏压部分,因此用这种方法分解拉压能量较为方便。然而,由于体积偏分分解中固有强度比范围的限制,采用上述方法难以准确地描述PBX材料的拉压不对称性。

3 考虑拉压不对称性的黏弹性相场法理论修正

3.1 相场变分理论

基于断裂相场法基本思想,本研究提出的黏弹性断裂系统能量泛函为:

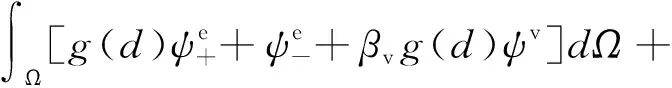
(1)

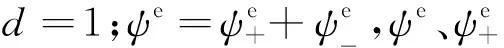
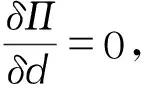
(2)

(3)

3.2 含损伤黏弹性本构模型

针对黏弹性本构模型,以广义Maxwell模型为例进行了研究。同时考虑体积变形黏弹性和剪切变形黏弹性的广义Maxwell模型如图2所示。

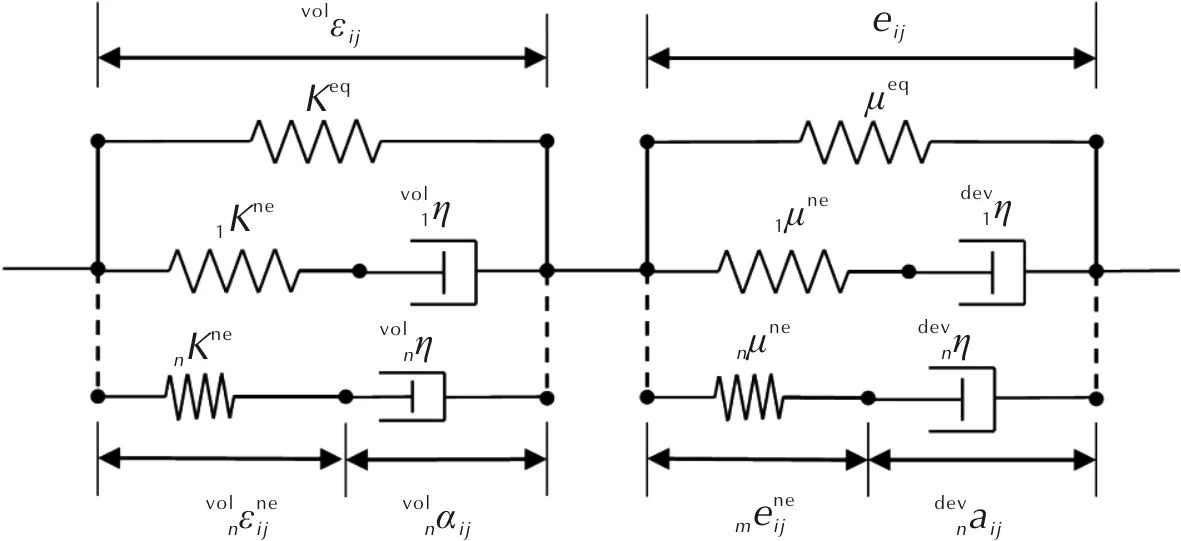
图2 广义Maxwell模型示意图Fig.2 Schematic diagram of the generalized Maxwell model

应变εij一般分解为体积应变volεij和偏应变eij:

(4)

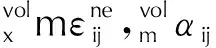
应力σij也表述为体量volσij和偏量devσij之和:

(5)

根据元件定义,同时为提高数值计算稳定性,采用Ambati[54]提出的混合相场模型,因此考虑相场引起损伤的本构模型为:

(6)

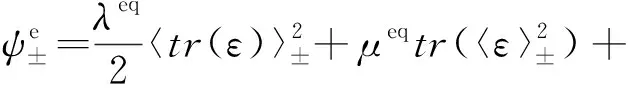
(7)

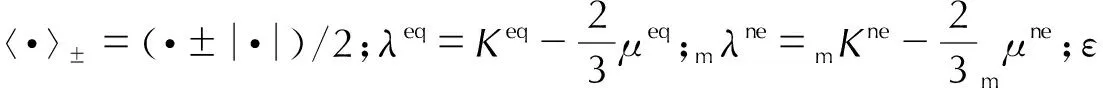
耗散能密度表示为:

(8)

以上即为本研究基于已有的黏弹性相场,考虑材料拉压不对称性的理论修正。

4 修正相场法的数值应用

针对上述建立的考虑拉压不对称性的黏弹性断裂相场模型,本研究采用COMSOL进行了数值实现,并通过多个实际算例来证明提出方法的有效性。同时在本研究中不研究耗散能贡献,因此βv=0,且非平衡项体积模量取为1Kne=0。

4.1 拉压过程仿真

4.1.1 单轴拉压过程仿真

首先是针对单轴拉压不对称性的预测准确性验证。针对PBX9502材料进行拉压过程仿真分析,具体几何尺寸、加载参数及试验结果参考文献[65-66]。仿真计算中采用中心对称模型,约束及加载方式同试验过程。采用最小二乘方法寻优获得的模型参数如下:Keq=1425MPa,μeq=380MPa,1μne=1130.5MPa,1τ=25.12s,Gc=13J/m2,l0=0.2mm,单元大小取为l0/he=2。计算得到的应力—应变曲线如图3所示。

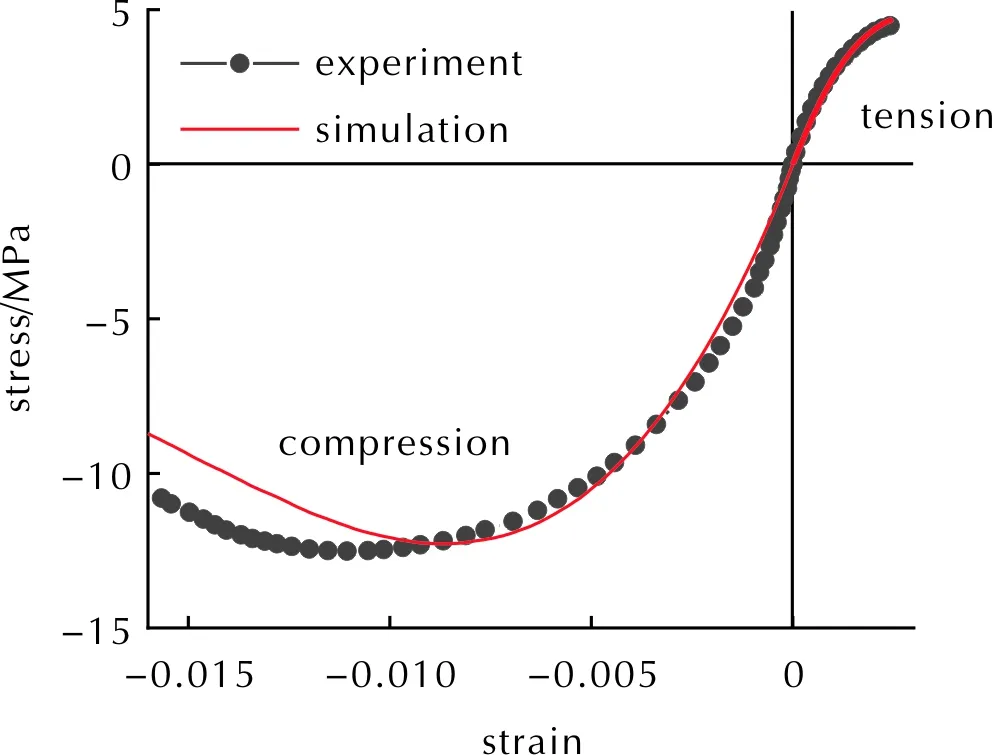
图3 实验与仿真得到的PBX9502应力—应变曲线对比Fig.3 Stress—strain curves for PBX9502 obtained from the experiment and simulation

由图3可知,计算得到的拉伸压缩应力—应变曲线与试验数据吻合良好。计算得到的拉伸强度和压缩强度分别为4.65MPa和12.28MPa,压缩拉伸强度比为2.64;实验所得拉伸及压缩强度分别为4.53MPa和12.52MPa,压缩拉伸强度为2.76;拉伸和压缩强度误差分别为1%和-2.2%。在本算例中仅采用了一阶广义Maxwell模型即可较为准确地描述该材料的拉伸和压缩曲线。

哑铃拉伸过程裂纹萌生扩展至断裂过程如图4所示。通过单轴压拉断裂行为的仿真分析,采用应变张量谱分解的相场法结合合适的本构模型可以精确地描述PBX材料的拉压不对称性特征。

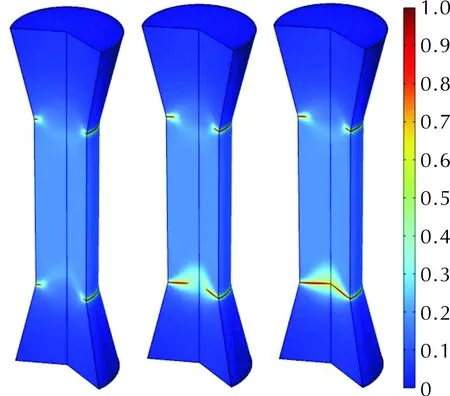
图4 PBX哑铃拉伸过程裂纹萌生、扩展及断裂过程(云图为相场自由度d)Fig.4 Crack initiation, extension and fracture processes during PBX dumbbell stretching (legend for phase field d)

4.1.2 围压压缩过程仿真

进一步开展该模型对于围压相关性的预测精度验证。针对名为EDC37的PBX材料,试验获得的不同围压下的应力—应变曲线如图5所示[8],围压越大,压缩强度越高。计算模型为一个三维单元,x-、y-和z-面采用简支约束,x+、y+面自由,加载过程中首先对x+、y+和z+面施加等静压,在此基础上,进一步对z+面通过位移进行等应变率加载。模型参数如下:Keq=444.6MPa,μeq=263.6MPa,1μne=167.7MPa,1τ=25.12s,Gc=5J/m2,l0=0.2mm,单元大小取为l0/he=2。

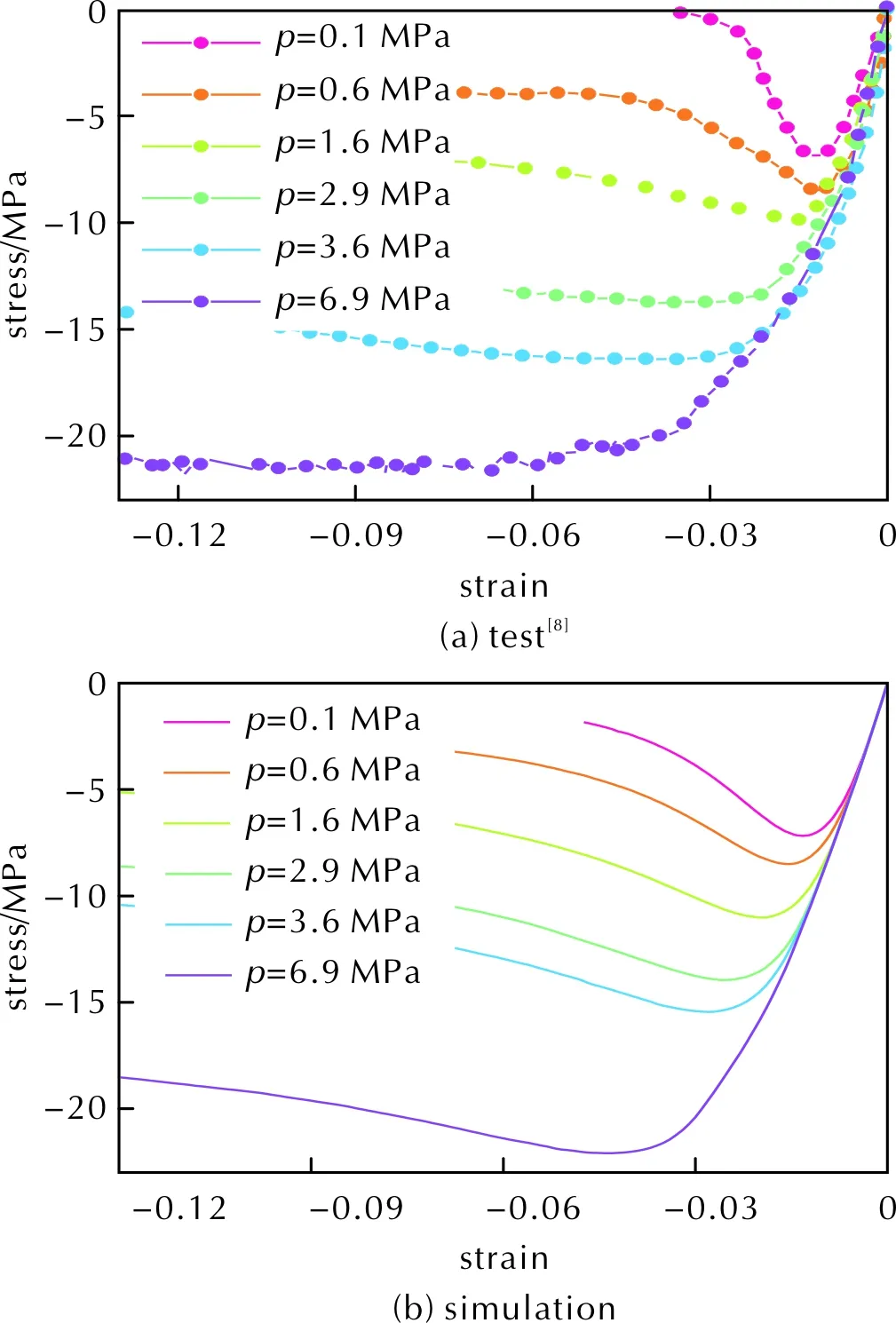
图5 不同围压下的压缩应力—应变曲线Fig.5 Compressive stress—strain curves at different isostatic pressures

不同围压下仿真与试验所得的应力—应变曲线如图6所示,二者规律一致。

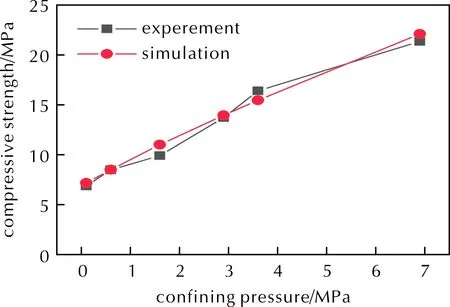
图6 实验与仿真获得的不同围压下压缩强度对比Fig.6 Comparison of the compression strengths obtained experimentally and simulatively at different confining pressures

从图6中进一步可以看出,压缩强度随着围压压力的增大呈线性增加;实验与仿真获得的压缩强度随围压变化的斜率分别为2.11和2.19,误差为2.8%,说明本研究提出的相场法可以较为准确描述不同围压下的压缩应力—应变曲线及压缩强度。

4.2 带孔板压缩过程仿真

为进一步验证提出的模型对于结构的预测精度,仿真分析了心带孔平板试样的压缩破坏过程。材料为PBX9502。Liu[67]通过实验研究了该构件在50℃下的压缩破坏试验,加载速率为1.27mm/min,并通过DIC获得了全场变形及裂纹演化过程。图7(a)为DIC获得的裂纹形貌,其为沿着上下圆弧处的竖直方向裂纹。

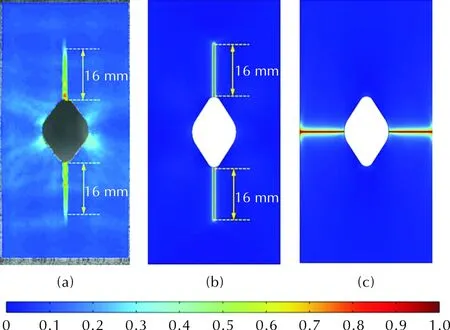
图7 裂纹形貌:(a)试验结果[67];(b)仿真结果-应变张量谱分解;(c)仿真结果-体偏分解[62]Fig.7 Crack morphology: (a) experimental results[67]; (b) simulation results of the proposed method; (c) simulation results of Shen et al[62]

仿真模型采用二维平面应力模型,约束同实验过程,底部固支、顶部约束水平方向位移同时按照1.27mm/min速率施加压缩位移,参数同4.1节。

首先从裂纹形貌上分析,本方法获得的结果与实验裂纹形貌较如图7所示,二者较为一致。由图7可知,其裂纹由上下圆弧中心开始萌生,然后沿着竖直方向开始扩展,形成上下对称的宏观裂纹,同时计算得到的裂纹上下、左右完全对称,证明本方法具有良好的计算鲁棒性。而采用体偏分解的方法[62]计算得到裂纹由左右圆弧处萌生并沿水平方向扩展,与试验结果不一致。进一步对比裂纹扩展长度均为16mm时的压缩载荷,试验与仿真获得的此刻载荷分别为8.62和9.62MPa,相对误差为11.6%。所以此方法不仅能计算准确的裂纹形貌,结合合适的本构模型后可以准确预测失效载荷。

4.3 PBX细观压缩过程仿真

本节通过PBX细观模型的断裂过程仿真来验证方法对于复杂裂纹的计算能力。首先基于PBX细观形貌分布特征[如图8(a)所示]建立了球形填充的PBX炸药细观结构模型,模型大小为1mm×1mm;然后参考文献[68]将界面进行弥散[见图8(b)],弥散宽度取为0.002mm;然后将球形晶体、黏结剂及界面区域设置不同材料参数;最后通过本方法进行竖直方向的单轴压缩仿真,加载速率为6.67×10-3mm/s。

图8 PBX压缩断裂演化图:(a)试验测得细观形貌;(b)建立并界面弥散后的细观仿真模型;(c)第一条裂纹萌生;(d)多裂纹萌生;(e)最终裂纹形貌;(f)试验测得最终形貌Fig.8 PBX compression fracture evolution diagrams: (a) experimentally measured microscopic morphology; (b) microscopic simulation model after building and interface dispersion; (c) first crack initiation; (d) multi-crack initiation; (e) final crack morphology; (f) experimentally measured final morphology

模型及参数如下:晶体采用线弹性模型,弹性模量为13.375GPa,泊松比为0.32,临界能量释放率为0.25N/mm。黏结剂采用广义Maxwell黏弹性本构模型,其弹性模量、剪切模量和松弛时间取值参考文献[69],泊松比为0.495,临界能量释放率为2.5N/mm。界面采用线弹性模型,弹性模量为20MPa,临界能量释放率为0.12N/mm;晶体、黏结剂及界面的弥散裂纹宽度均取为0.002mm。

图8(c)～(d)为压缩过程微观裂纹萌生、扩展-融合直至失效裂纹形貌图。图8(c)为第一条裂纹萌生,图8(d)为多条裂纹萌生并扩展,图8(e)[图9为图8(e)放大图]为多裂纹分叉融合后形成的最终断裂形貌,且与试验结果[图8(f)]较为吻合。通过图8(c)～(d)可知,该方法可自然地进行多裂纹萌生、扩展、分叉和融合等复杂断裂过程的仿真计算扩展,相对于扩展有限元等方法具有明显优势。

图9 最终时刻裂纹形貌(黄色虚线框为裂纹分叉/融合区域)Fig.9 Final crack morphology (yellow dashed box shows crack bifurcation/fusion area)

5 结 论

(1)理论方面,结合广义Maxwell黏弹性本构模型,采用应变张量谱分解的方法对弹性势能进行分解,认为只有拉伸弹性能和耗散能驱动损伤演化和裂纹形成,构建了考虑拉压不对称性的黏弹性断裂相场模型。

(2)材料力学行为验证方面,采用提出的模型对典型PBX材料的单轴拉伸压缩过程进行仿真,拉伸压缩强度描述误差不大于2.2%,证明了提出的方法可精确描述PBX材料的拉压不对称性;同时对典型PBX材料不同围压压缩过程进行模拟,强度随围压变化斜率误差不大于3%,证明了提出的模型可不经额外处理而自然地描述不同围压下的力学性能。

(3)结构断裂行为验证方面,采用提出的模型计算了典型PBX带孔板压缩过程,从裂纹形貌上与试验结果完全一致,从相同裂纹长度时载荷误差小于12%,且计算具有较好的鲁棒性;采用提出的模型仿真计算了PBX细观结构模型的压缩过程,证明了提出的模型依然可以自然地进行多裂纹萌生、扩展、分叉及融合复杂断裂行为的仿真预测。

(4)黏弹性断裂相场模型可同时考虑PBX材料复杂的力学特征以及PBX结构复杂的断裂行为;针对PBX炸药断裂行为的仿真计算,相场法具有显著的优势及潜力。