准静态拉伸下PBX力学性能的三维细观模拟
2023-07-14罗慧灵曹落霞李华荣张朝阳
罗慧灵,刘 柳,曹落霞,李华荣,周 阳,张朝阳,,杨 宏
(1.西南石油大学 化学化工学院,四川 成都 610500;2.中国工程物理研究院 化工材料研究所,四川 绵阳 621900)
引 言
高聚物黏结炸药(Polymer Bonded Explosive,PBX)是一种由高能单质炸药以及少量高聚物黏结剂组成的混合炸药,具有能量高、安全性好等优点,被广泛应用于固体推进剂以及武器战斗部[1-4]。PBX不仅是武器的毁伤源,也是武器结构中最为薄弱的承力环节之一,其在拉伸、压缩、剪切等外界加载下的力学行为直接影响了武器部件在运输、贮存以及使用过程中的结构稳定性,从而决定了武器的可靠性与安全性。
作为一种典型的复合材料,PBX内部包含大量的裂纹、界面及孔洞等细观结构,PBX细观结构与其力学性能之间的关系一直以来都是含能材料领域研究人员关注的热点。实验方面,Siviour等[5]在研究RDX基PBX时发现,增加颗粒尺寸会降低PBX的强度,且细颗粒会使得应力—应变曲线表现出更为明显的屈服特征。肖磊等[6]发现在微米级RDX中加入一定量的纳米级RDX,能够使PBX的抗拉强度从0.66MPa提升至0.77MPa。此外,Herman等[7]发现降低颗粒尺寸也会显著增加PBX的抗压强度。模拟方面,王竟成等[8]采用有限元方法研究了颗粒体积分数对HMX基PBX弹性性能的影响,发现颗粒体积分数的升高会导致杨氏模量和剪切模量增加。Yang等[9]研究了界面强度及断裂能对高颗粒填充(>90%)复合材料拉伸性能的影响,结果表明界面强度的升高会显著提升材料整体的抗拉强度,而断裂能的变化会改变材料的开裂路径,影响其失效模式。
PBX内部结构十分复杂,实验中PBX的细观结构难以被准确量化,以至于只能获得二者之间的定性关系。基于代表性体积元(Representative Volume Element, RVE)的数值模拟技术是获得细观结构与宏观力学性能定量关系的有效手段。由于建模较为复杂以及计算消耗偏大,当前大部分的数值模拟都采用二维RVE代表PBX炸药,但是,二维模型仅仅是真实三维模型的一个切片,因此影响了数值模拟结果的准确性。不同二维模拟获得的结果往往存在较大差异,如Banerjee等[10-11]的研究表明,86%HMX/14%Estane体系的杨氏模量约为4~6GPa,针对相同体系的不同研究给出的杨氏模量仅有0.67~2.7GPa[8, 12],两者之间最高可相差10倍。此外,Arora等[13]发现,即使是相同的二维模型,采用平面应变假设和平面应力假设都会导致获得的应力—应变曲线产生显著差异。因此,构建三维模型对于提高PBX力学性能预测的准确性具有重要意义。
本研究以HMX/Estane体系为研究对象,基于自编的建模程序,构建了PBX三维RVE模型,计算了准静态单轴拉伸条件下PBX的拉伸力学性能,并探索了炸药颗粒体积分数、炸药颗粒尺寸以及界面性能对力学性能的影响规律及机制,研究结果加深了对PBX细观结构与宏观力学性能之间关系的认识,并对如何有效提升PBX抗拉强度提出了建议。
1 模型与方法
1.1 PBX细观模型
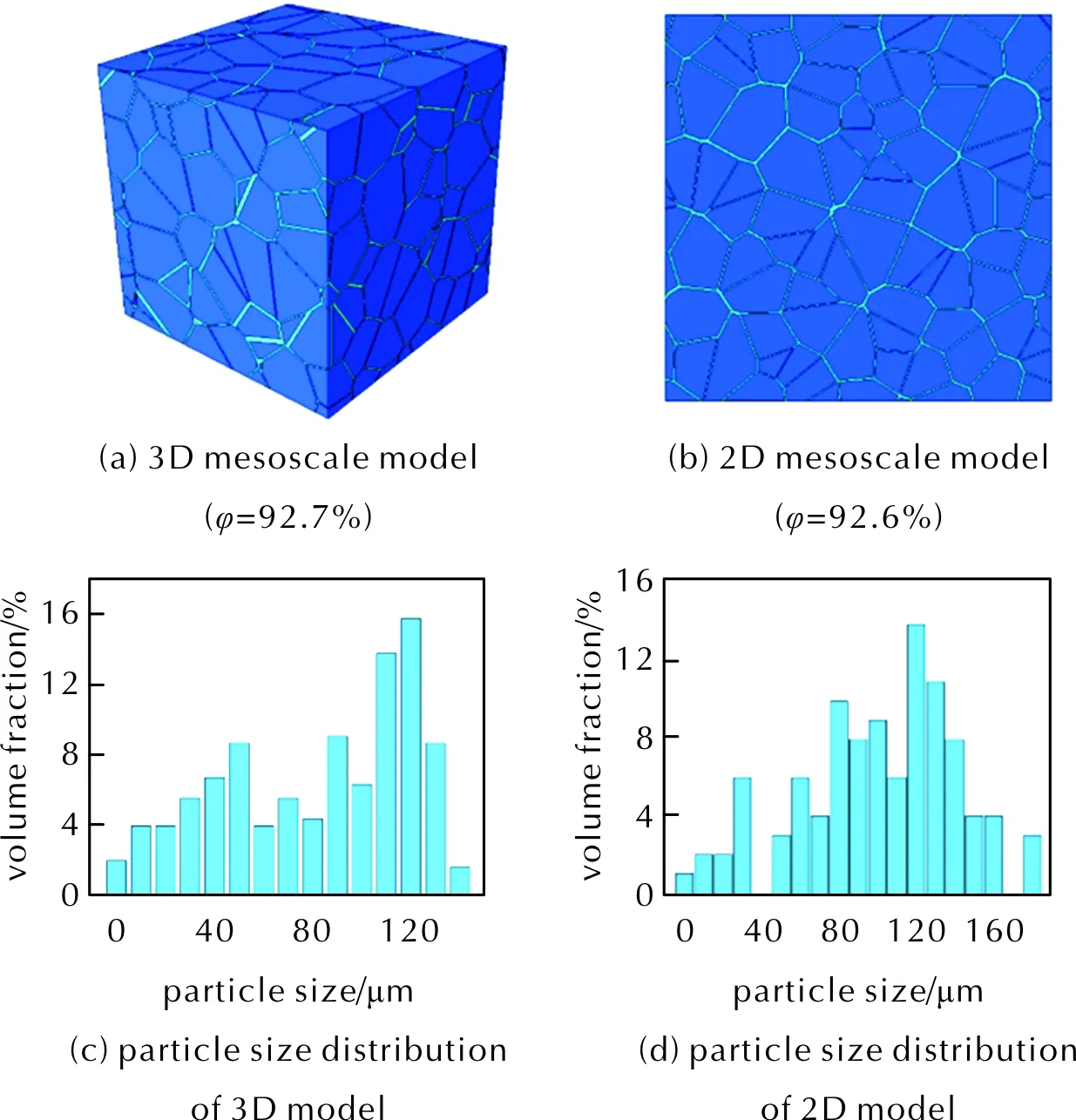
图1 PBX细观模型及颗粒尺寸Fig.1 The mesoscale models and particle sizes of PBX
1.2 本构模型
采用线弹性[14]以及各向同性塑性[15]本构模型描述HMX,具体参数为:杨氏模量E=25325MPa,泊松比ν=0.25,密度为1.9g/cm3。塑性参数见表1。
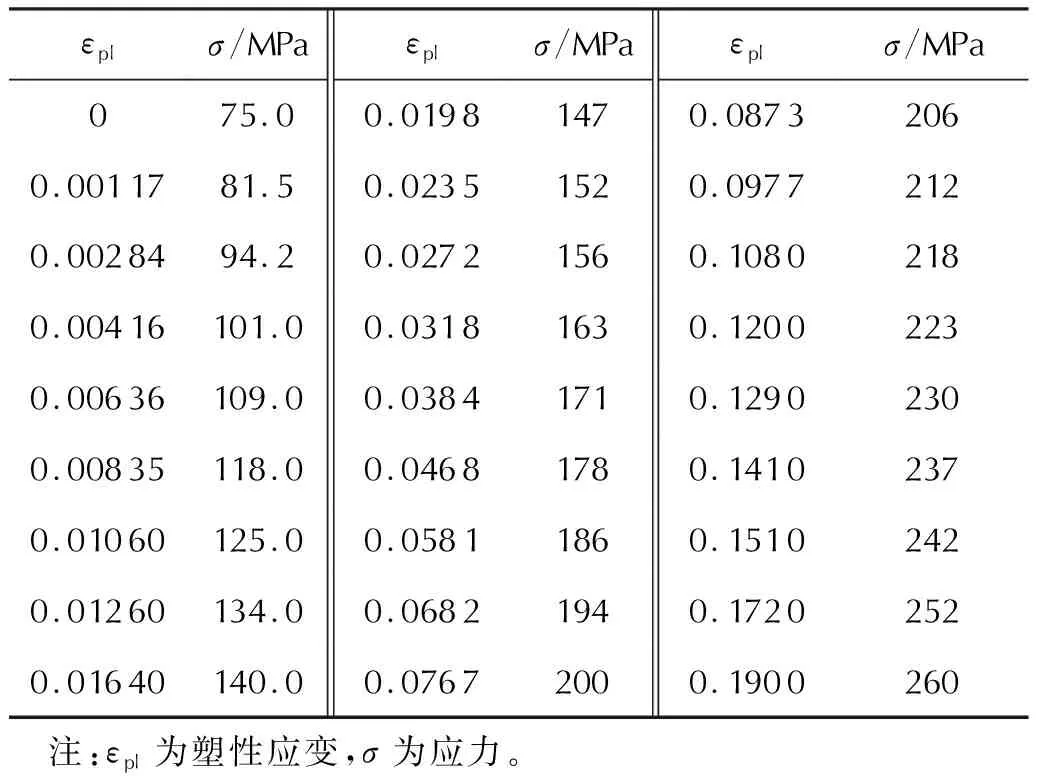
表1 HMX塑性参数Table 1 Plasticity parameters of HMX
采用广义麦克斯韦模型(Generalized Maxwell Model,GMM)描述Estane5703的黏弹性,使用Prony级数表征剪切模量G随松弛时间的变化[16],具体参数见表2。
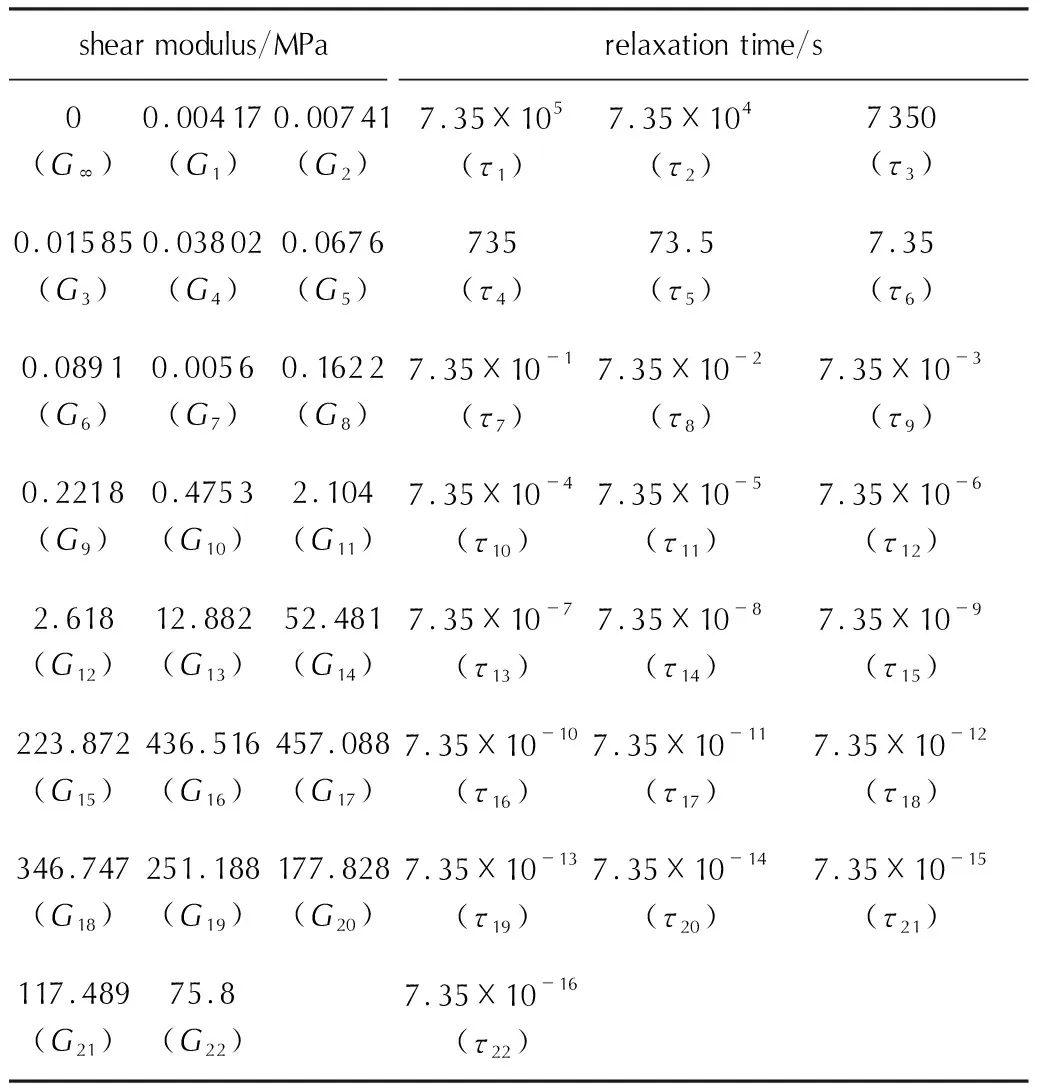
表2 Estane5703的黏弹性参数Table 2 Viscoelastic parameters of Estane5703
单轴拉伸条件下,炸药颗粒与黏结剂之间界面的脱粘是导致损伤的主要模式,因此,对界面的描述直接关系到拉伸性能计算结果的可靠度。采用双线性内聚力模型描述颗粒-黏结剂界面,如图2所示,stage I表示线弹性阶段,当界面之间的位移达到δ0时,界面损伤开始出现,stage II表示损伤阶段,在此阶段中,界面的刚度会随着位移的增加而降低,当位移到达临界值δc后,界面完全失效。
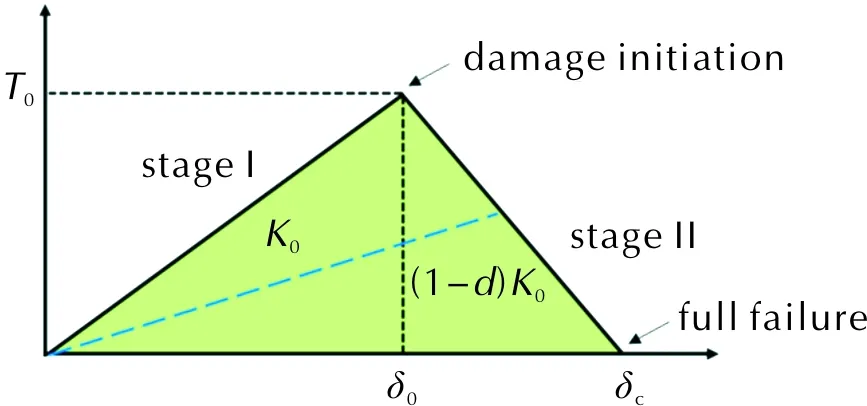
图2 双线性内聚力模型示意图Fig.2 Schematic diagram of bilinear cohesive zone model
采用最大应力准则以判断界面是否损伤,如下式所示:
(1)
式中:下标n和t分别代表界面的法向与切向,〈〉为Macaulay bracket算符,定义为〈x〉=max(x,0),表示在压缩条件下界面不会发生损伤,使用模态独立的损伤模式。
断裂能G表征了界面损伤过程中消耗的能量,定义为牵引力T与界面位移δ所围成的阴影区域的面积,如式(2)、式(3)所示:
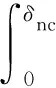
(2)
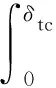
(3)
法向与切向的界面参数见表3[14, 17]。

表3 双线性内聚力模型参数Table 3 Parameters of bilinear cohesive zone model
1.3 网格与边界条件

图3 三维细观模型的网格及边界条件Fig.3 Mesh and boundary conditions of the 3D mesoscale model
2 结果与讨论
2.1 网格收敛性及准静态验证
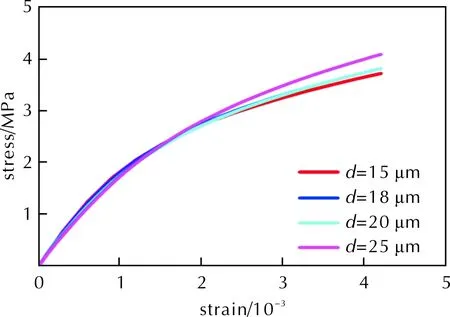
图4 不同网格尺寸下三维模型(=92.7%)的应力—应变曲线Fig.4 Stress—strain curves for 3D models (=92.7%) with different mesh sizes
由图4可知,当网格尺寸从25μm降低至20μm时,应力—应变曲线的弹性段与非弹性段都发生了明显的改变,而当网格尺寸从20μm变化至15μm时,应力—应变曲线几乎重合,说明在网格尺寸为18μm的条件下,计算结果已经达到了收敛。
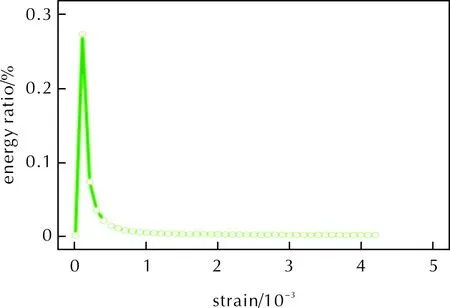
图5 三维模型(=92.7%)的动能/内能比随应变的变化Fig.5 Variation of kinetic/internal energy ratio with strain in 3D model (=92.7%)
由图5可知,在拉伸过程中,体系的动能/内能比最大仅为0.27%,远小于5%,因此可视为准静态加载。
2.2 模拟与实验的比较
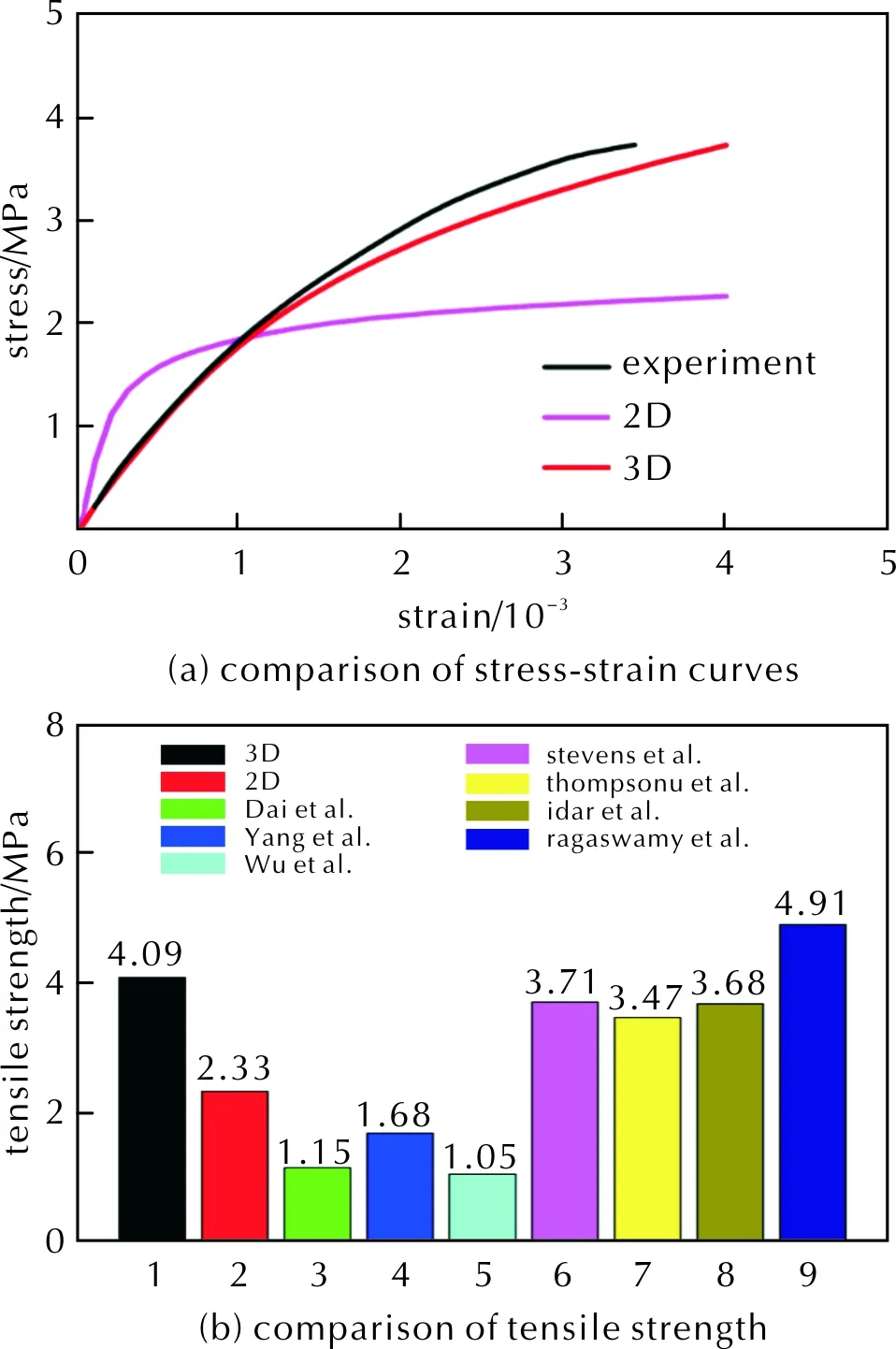
图6 模拟结果与实验结果的比较Fig.6 Comparison of simulation results with experimental results
图6(b)给出了抗拉强度的计算结果、二维模拟文献结果以及实验结果。大部分实验工作[19-20,22-23]获得的PBX 9501抗拉强度范围均在3.4~5MPa之间(图中数据5~9),与本研究的三维模拟结果(4.09MPa,图中数据1)较为吻合。值得注意的是,之前基于二维模型的数值模拟工作[9, 21]给出的HMX/Estane体系的抗拉强度在1.15~1.68MPa之间(图中数据3~4),远小于本研究获得的三维结果,说明二维模型会严重低估PBX的抗拉强度。但是,本研究的二维结果(2.33MPa,图中数据2)与二维文献值较为接近,少量的误差可能来源于颗粒形状以及粒径的差异,这证实了本研究模拟方法的有效性。
2.3 颗粒体积分数对力学性能的影响
PBX的宏观力学性能与其细观结构密切相关,本研究首先探索了颗粒体积分数的影响,图7(a)给出了在不同的颗粒体积分数下,基于三维细观模型获得的应力—应变曲线。结果表明,随着颗粒含量的升高,应力—应变曲线会整体上移,PBX的杨氏模量会显著升高,抗拉强度也会有一定程度的升高。图7(b)给出了基于二维模型获得的应力—应变曲线,可以看出,虽然随着颗粒含量的升高,二维模型获得的应力—应变曲线也会逐渐上移,但是曲线表现出更为明显的屈服现象,导致获得的抗拉强度普遍低于三维模拟结果。不同颗粒体积分数下PBX的抗拉强度值如图7(c)所示。

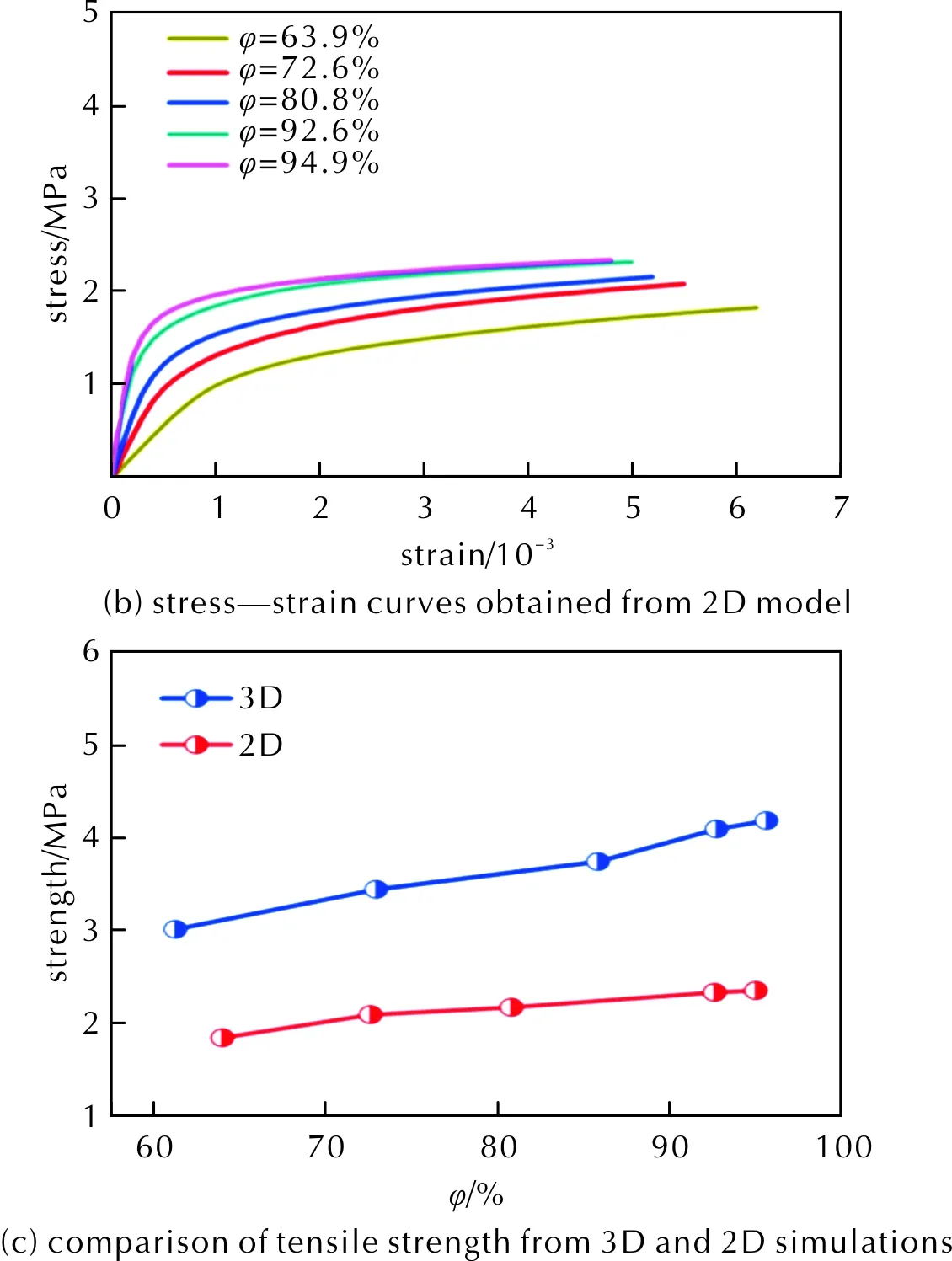
图7 颗粒体积分数对力学性能的影响Fig.7 Effect of particle volume fraction on mechanical properties
结果表明,二维与三维模型获得的抗拉强度差异巨大,当体积分数为72%左右时,三维结果比二维结果高出约39.2%。但是,两种模型都表明,颗粒体积分数的增加并不会导致抗拉强度发生显著变化,如三维结果表明,当颗粒体积分数从61.2%升高至95.6%时,抗拉强度从3.01MPa增加至4.18MPa,变化值仅为1.17MPa(38.9%),二维结果也表明,颗粒体积分数从63.9%升高至95.0%,仅会导致抗拉强度变化约0.51MPa。
图8给出了三维模型和二维模型在相同的应变下模型内部在拉伸方向(y方向)的应变分布云图。
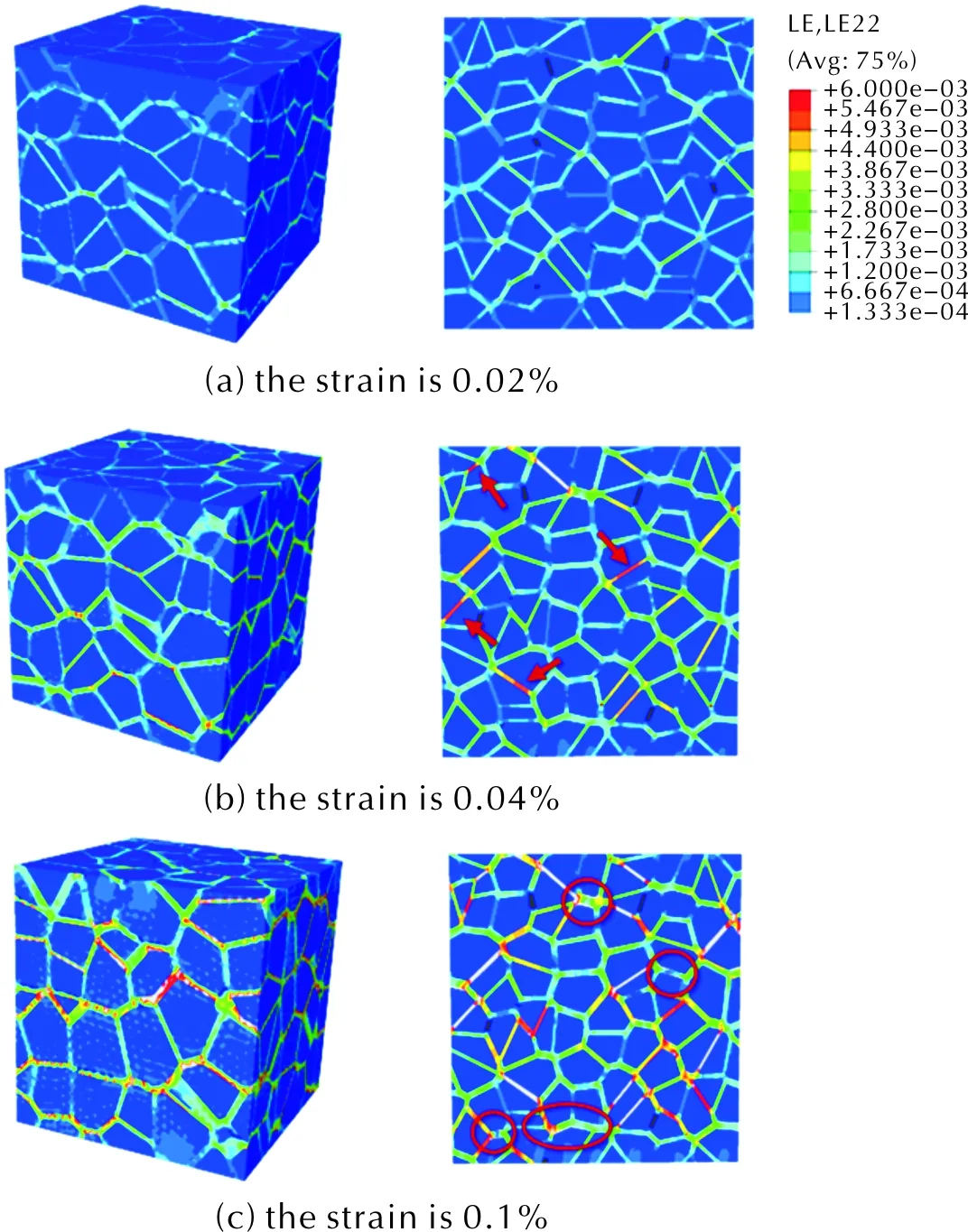
图8 三维(=72.9%)和二维(=72.6%)模型的应变云图Fig.8 Strain clouds for the 3D (=72.9%) and the 2D (=72.6%) model
由图8可知,拉伸条件下黏结剂及炸药颗粒-黏结剂界面会先发生较大变形,当加载面应变为0.02%时,三维和二维模型中的应变分布都较为均匀,未出现应变过大的位点,但是当加载面应变达到0.04%时,二维模型中的界面处出现了多个产生大应变的局部位点(箭头所指位置),表明在该位点发生了明显的界面脱粘,当加载面应变达到0.1%时,二维模型已经观察到了多处微裂纹(圆圈处),而三维模型中还未观察到微裂纹的产生。上述结果表明二维模型在拉伸下更容易发生界面脱粘,形成微裂纹,从而导致二维模型表现出更为明显的屈服现象,成为了二维模型拉伸强度偏低的原因。
2.4 颗粒尺寸对PBX力学性能的影响
颗粒尺寸是影响PBX性能的重要参数,也是实验中最常研究的细观参数之一。实验上,PBX中HMX颗粒的尺寸为100~200μm[24-25],因此,本研究构建的PBX模型中选取的颗粒粒径为80~160μm。图9(a)给出了三维模型中不同颗粒尺寸下PBX的应力—应变曲线。结果表明,颗粒尺寸的变化并不会导致PBX的杨氏模量发生改变,Verbeek等[26]的研究表明对于两相复合材料,颗粒的尺寸从50μm增加至350μm不会对材料的杨氏模量产生显著影响,与本研究获得的结果一致。但是,颗粒尺寸的升高会导致抗拉强度降低,如当颗粒尺寸从120μm升高至160μm时,PBX的抗拉强度从4.09MPa降低至3.56MPa,降低了13%,该结果与实验结果定性相符[6]。
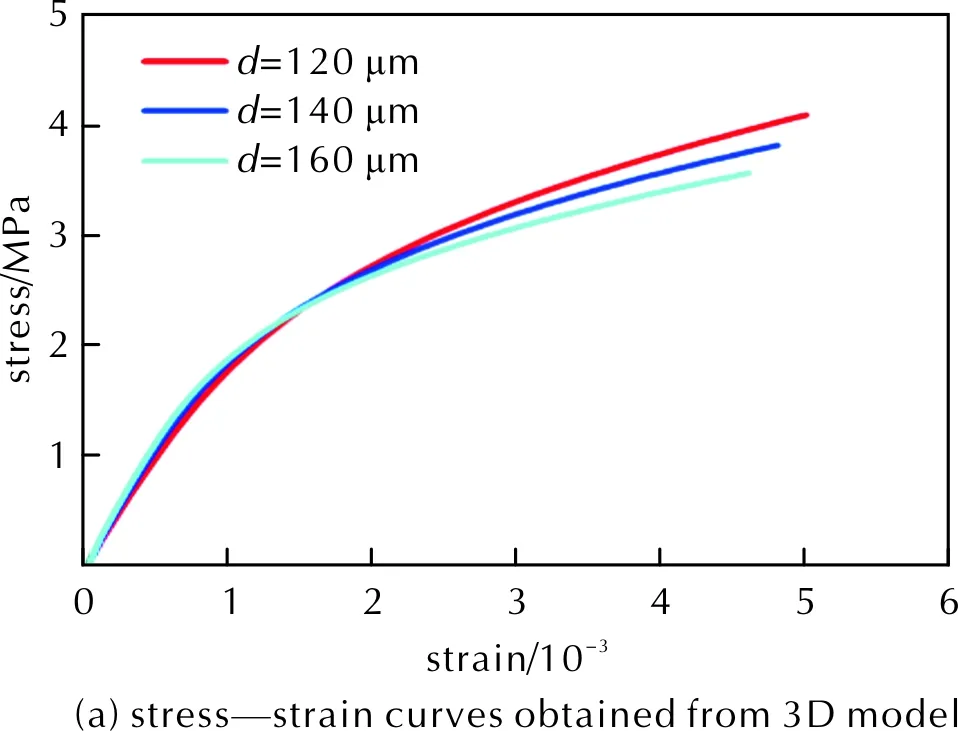
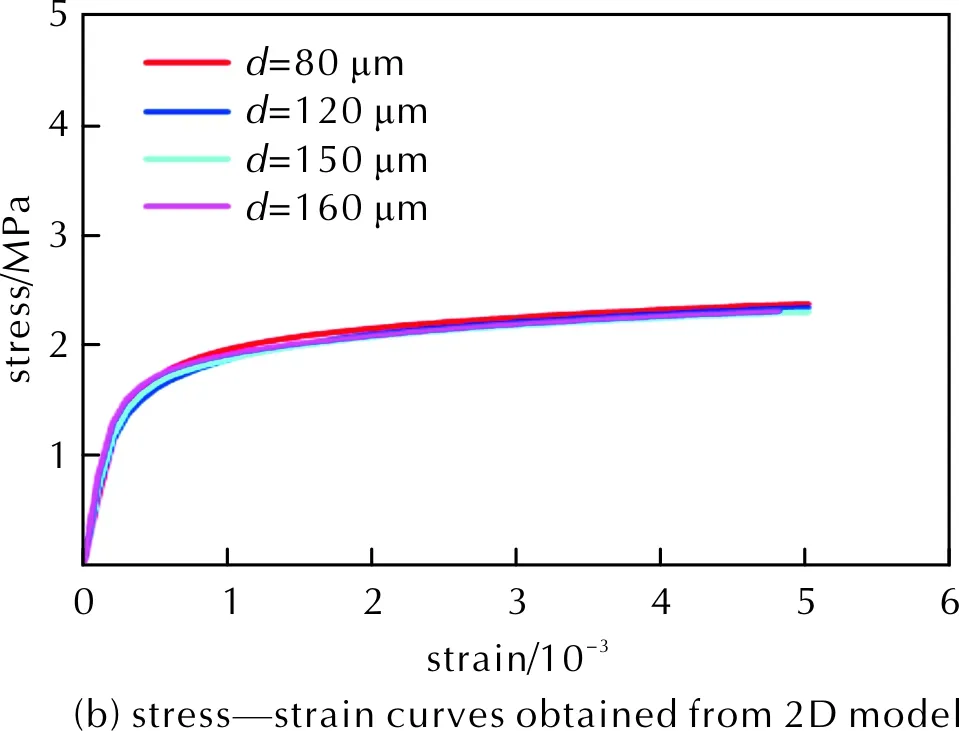
图9 三维及二维模型中颗粒尺寸对应力—应变曲线的影响Fig.9 Effect of particle size on stress—strain curves in 3D and 2D models
颗粒尺寸对强度的影响可能与颗粒堆积有关,相比于细颗粒,粗颗粒之间容易产生不紧密堆积,导致应力集中,从而使界面产生局部脱粘。与三维结果不同,图9(b)中的二维模拟结果表明,颗粒尺寸从80μm增加至160μm并不会导致抗拉强度发生明显变化,这与二维模型在拉伸下更容易形成微裂纹有关,微裂纹的产生主导了应力—应变曲线的非弹性变化,从而掩盖颗粒尺寸对PBX强度带来的微小影响。
2.5 界面性能对PBX力学性能的影响
在拉伸加载下,炸药颗粒-黏结剂界面的脱粘是PBX发生损伤的主要模式,因此,界面强度是影响PBX拉伸力学行为最为关键的参数之一[27]。本研究首先研究了在颗粒-黏结剂界面断裂能不变的条件下,界面强度的变化对PBX力学性能的影响。图10(a)给出了在不同的界面强度下,PBX的应力—应变曲线,可以看出,界面强度的增加会导致界面更难发生开裂,导致PBX开始发生非弹性变形所对应的应变升高,使得抗拉强度显著增加。图10(b)给出了包含不同颗粒体积分数的PBX中抗拉强度随界面强度的变化曲线,结果表明,在高颗粒含量下,界面强度对抗拉强度的影响更为明显。
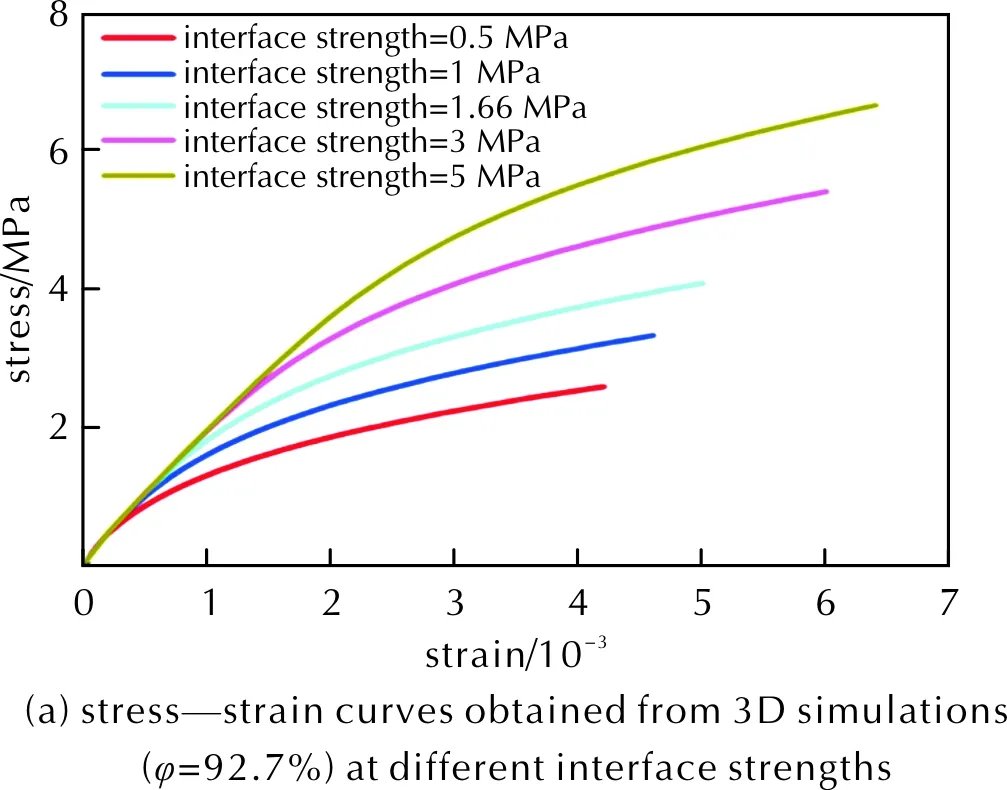

图10 界面强度对拉伸性能的影响Fig.10 Effect of interface strength on tensile properties

图11 不同断裂能下三维模拟(=92.7%)得到的应力—应变曲线Fig.11 Stress—strain curves obtained from 3D simulations (=92.7%) at different fracture energies
由图11可知,断裂能的升高也会导致抗拉强度的显著提升,如当断裂能从0.091N/mm增加至0.16N/mm时,抗拉强度会从4.09MPa升高至5.22MPa,升高了27.8%。上述结果表明,界面性能虽然不会影响PBX的弹性性能,但是会导致抗拉强度发生显著变化,界面强度以及断裂能的提升都会导致抗拉强度大幅度升高。
3 结 论
(1)采用自编的建模程序构建了HMX基PBX的三维模型,计算了其在准静态单轴拉伸下的应力—应变曲线,与PBX 9501的实验数据高度吻合,此外,三维模拟获得的抗拉强度结果也与实验一致,说明基于三维细观模型的数值模拟能够很好地预测PBX的力学性能。
(2)计算了颗粒体积分数为61.2%~95.6%的PBX炸药在拉伸下的力学性能,发现随着颗粒含量的升高,PBX的杨氏模量和抗拉强度都会升高,但是抗拉强度的变化并不明显,颗粒体积分数从61.2%升高至95.6%时,抗拉强度仅增加1.17MPa。二维模型在拉伸下表现出更为明显的屈服现象,三维模型获得的抗拉强度比二维模型高约40%,这与二维模型更易发生界面脱粘有关。
(3)研究了颗粒尺寸对PBX力学性能的影响,发现颗粒尺寸的升高并不会影响杨氏模量,但是会降低抗拉强度,颗粒尺寸从120μm升高至160μm,使得抗拉强度降低了13%。
(4)基于双线性内聚力模型,计算了界面强度以及断裂能的变化对PBX拉伸性能的影响,发现界面强度和断裂能的升高会导致抗拉强度发生显著变化,界面强度从0.5MPa升高至5MPa,抗拉强度会从2.58MPa升高至6.82MPa,断裂能从0.091N/mm增加至0.16N/mm,抗拉强度会从4.09MPa升高至5.22MPa。因此,相比于改变颗粒粒径,增加炸药颗粒-黏结剂之间的界面强度和界面能是提高PBX抗拉强度更为有效的方式。
