基于生态驾驶的道路合流区车辆运行状态估计

2023-07-14朱云波夏玉兰王玥然陆久飞谢济铭

北京工业大学学报 2023年7期

朱云波, 夏玉兰, 王玥然, 黄磊, 陆久飞, 谢济铭

(1.云南省交通科学研究院有限公司, 昆明 650011; 2.昆明理工大学交通工程学院, 昆明 650500; 3.云南省交通规划设计研究院有限公司, 昆明 650041)

快速路系统中,车辆时常需汇入或驶离主线,当进入主线的匝道和驶离主线的匝道距离较近时,会形成汇入汇出车流冲突区,即合流区[1]。由于合流区道路线型的限制及驾驶人驾驶意图的差异,易产生频繁的急加减速、怠速等现象,导致车辆燃油经济性的降低和污染物排放的增加[2]。因此,改善驾驶员驾驶行为,倡导生态驾驶,成为道路交通节能减排的一条可行之路。

在现有的生态驾驶策略中,大量学者从车辆运行状态的动态变化特征入手,探索合适的行驶策略,以期提高燃油经济性、减少污染物排放量。经典车辆运行状态估计方法为参数模型方法,其中多元线性回归[2]因操作简便且能显著表征各因素之间的相关程度,被广泛应用于交通速度预测,并取得了一系列研究成果。刘硕等[3]利用实车实验数据研究了上海市8条城市地下道路的车速分布特征及运行车速,并基于道路线形建立了多元线性回归车速预测模型。马聪等[4]基于曲率变化率、曲度等因素进行多元回归,建立了隧道路段出入口及隧道内运行速度预测模型,结果显示所建模型能够精确预测隧道各路段运行速度。张驰等[5]利用使用链式开普勒雷达测速仪实时采集立交桥入口处小客车运行速度,建立了小客车在合流点及加速车道终点处运行速度预测模型。徐进等[6]基于隧道出入口断面数据分析了车辆行驶车速的变化规律和影响因素,建立了运行速度预测模型。

此外,车辆运行状态估计需要大量高质量数据作为支撑,一些学者利用驾驶模拟器或实车测试提取数据展开研究,不过较难获得所有车辆轨迹、掌握大量车辆车速时空变化特征。2006年,美国联邦公路局公开了下一代交通仿真(next generation simulation, NGSIM)车辆轨迹数据集[7],此后至今,国内外许多学者均基于NGSIM展开车辆微观参数建模等研究,但受制于道路条件、交通规则及文化差异,NGSIM难以反映国人真实驾驶行为特征。近年来,利用采集成本低、覆盖范围广的无人机视频采集技术采集并提取微观轨迹数据,应用于交通流特征分析、交通运行建模领域,虽取得了不错成效,但仍处于探索阶段[8-9]。

综上所述,既有研究存在如下3个方面的缺陷,还需进一步完善和探索:1)大都面向平直路段,较少针对多车道交织区合流段等道路节点部位进行车速预测研究[10-11];2)采用历史统计数据直接预测车辆运行速度,未深入描述个体车辆加速度与速度之间的关联性[12];3)传统数据采集方式速度样本少、精度低,难以适用于未来大规模车路协同运行环境实际需求[13]。

因此,针对城市道路合流区生态驾驶策略的研究,缺乏对真实场景下运行车辆的车速特性分析。本文基于无人机视频在捕获时空信息方面的高效性,以及数据采集的完整性,选取典型交织区,利用无人机视频采集自然驾驶状态下车辆运行视频数据,提取全样本高精度车辆速度、加速度信息,得到其分布特征、变化规律,基于多元线性回归构建车速状态估计模型,验证所提模型的有效性。

1 数据采集及提取

为精细捕捉该交织区车辆速度复杂特性,选取重庆市内环快速路某多车道交织区为研究对象。在天气良好的工作日,利用无人机悬停于交织区上方120 m采集车辆运行高清视频,如图1所示。

实验人员在交织区进行了2类观测实验:实验1为8:30—10:00车流高峰时段;实验2为18:30—19:30车流平峰时段。

在观测实验视频中发现一些交通特性:1)高峰时段,存在路径转换需求的车辆进入交织区产生大量换道行为,导致运行速度有所下降,极易出现拥堵状况,瓶颈效果显著,拥堵自分流区蔓延至紧邻上游路段; 2)平峰时段,大部分车辆仅在交织区减速,此外,合流区与分流区车辆运行状态都较为相似且稳定。

基于多尺度核相关滤波(kernel correlation filter, KCF)车辆跟踪优化算法,从航拍视角对运动车辆进行自动识别和跟踪,构建交通流信息与车辆行为信息基础数据库[14]。算法通过框选跟踪目标车辆,提取并记录车辆位置与状态信息。此外,针对交织区存在遮挡、背景复杂、目标间距小、多个相似目标、光线变化等复杂环境进行算法优化,通过多尺度窗口(放大/正常/缩小)迭代计算获取多组方向梯度直方图(histogram of oriented gradient, HOG)特征,以此降低目标由于环境干扰和比例变化所造成的影响[15]。时间分辨率0.1 s、空间分辨率0.1 m/像素,数据颗粒度小,检测结果精度高。

2 交通特性分析

2.1 交织区车速运行特征分析

2.1.1 车速统计特性

利用卡尔曼滤波对速度数据进行平滑处理消除毛刺后,采用Gaussian分布拟合车速频率分布曲线,得到交织区速度频率分布及数据拟合如图2所示,可以看出:

1) 整体而言,平峰时段车速基本符合Gaussian分布,车速离散、分布均匀;高峰时段车速分布相对紊乱无序,车速集中、分布错落,说明本文车速采集信息符合自然驾驶实验数据统计规律[16]。

2) 平峰时段车速分布于[0,60]km/h,集中于(25±5)km/h,说明平峰时段车辆运行仍未达到85分位限速值(60 km/h)标准,可能的原因是,多车道交织区车辆需连续跨越多条车道到达目标车道,驾驶人在换道决策、路径规划过程中,导致运行车速降低。

3) 高峰时段车速分布于[0,30]km/h,集中于(7±5)km/h,说明高峰时段大部分车辆运行低于15分位限速值,表明车辆行驶极为缓慢,且95%车辆车速未达到限速值的50%,由于车辆驶入交织区是一个车辆聚集过程,车辆之间相互影响较大,运行车速降低,出现拥堵情况,瓶颈效应明显,导致车速表现为不均匀的左偏分布。

2.1.2 加速度特性

随机抽样高峰、平峰时段加速度空间分布曲线各3条,变化趋势如图3所示。

图3 平(高)峰状态交织区加速度空间分布特性Fig.3 Spatial distribution characteristics of acceleration in the interleaved area of flat (high) peak state

1) 高峰时段拥堵状态下,车辆加速度总体呈现出先波动再缓慢增长的趋势,波动范围为[-0.75,1.75]m/s2。说明车辆从汇入交织区到交织段结束的区间内,由于拥挤而不断小范围的加速减速,导致加速度在0 m/s2上下波动,当到达分流区拥堵减缓,车辆开始加速,使得加速度逐渐趋于0 m/s2的上方并有增长的趋势。

2) 平峰时段畅通状态下,车辆加速度呈现出左高右低的下降趋势,其变化范围为[-1.5,2.6]m/s2。体现为车辆从匝道和主线汇入时速度较大并随之减速,因此加速度出现了明显的波峰,随后加速度不断减小,甚至在分流区以后,几乎都为负值,车辆减速,平稳缓慢驶离交织区。

2.2 合流区车速分析

由前述分析结果可知,交织区高峰时段车速呈紊乱、随机、离散等复杂特性,为进一步掌握合流区交通运行规律,本节针对合流区车速特性展开研究。

将平(高)峰时段合流区的车速数据样本,分别按照从大到小的顺序排列后,对数据进行编号(1～N),N为样本数,随后进行对数拟合,对数分布为

y=a-bln(v(t)+c)

(1)

式中:a、b、c为待标定参数;v(t)为t时刻车辆瞬时车速。参数通过极大似然估计求得,结果如表1所示。

表1 平(高)峰合流区速度拟合结果Table 1 Velocity fitting results of the flat (high) peak confluence area

本文提取微观轨迹数据广泛应用于风险预测[15]、换道建模[17]、车速预测[18]等方面,针对车速估计问题,分别采集平峰、高峰样本20 445、150 860组[18],通过对合流区车速进行描述性统计分析,发现平峰时段合流区偏度、峰度分别为0.34、0.13,高峰时段偏度、峰度分别为0.94、2.54,说明平峰、高峰时段车速基本服从高斯分布[17]。相较于平峰时段,高峰时段车速均值、标准差、50分位值、85分位值分别降低74.83%、59.6%、70.26%、69.38%[18],此外,由图4可知,平峰、高峰时段车速差异显著,表明高峰时段合流区车流密度较大,通行速度缓慢,交通拥堵现象明显。

图4 合流区速度描述统计Fig.4 Speed descriptive statistics in the confluence area

3 车辆运行状态估计模型

3.1 纵向加速度与速度关联度分析

基于纵向加(减)速度与行驶车速关系,可构建高峰时段多元线性回归车速估计模型[19]。首先,需分析二者分布规律,因此,绘制纵向加(减)速度-行驶车速散点图及轮廓线,再以加减速行为开始时刻的速度值,即初速度为分组依据,组间距为5～10 km/h,统计落在每一分组的50%、75%、85%、90%特征百分值(V50、V75、V85、V90),得到加(减)速度特征百分位值-初速度关系,如图5所示。

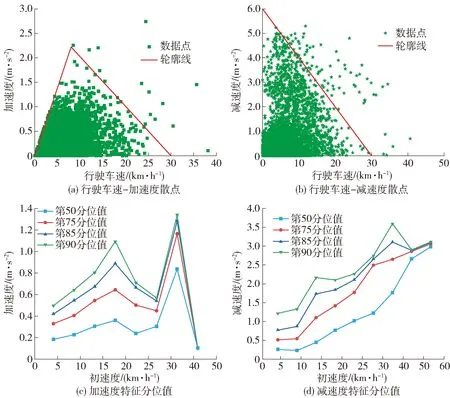
图5 车速与加(减)速度之间的关系Fig.5 Relationship between speed and acceleration (deceleration) speed

由图5(a)可见,加速度与行驶车速关系呈不等腰三角形,加速度分布于[0,3.0]m/s2,与文献[20-21]的研究结论相符,说明行驶车速较低时,驾驶人提速的愿望较为迫切,且汽车加速储备动力较足,因此可快速得到较大的加速度值,而随着合流区实际运行条件的限制,驾驶人不得不减小加速度行驶。

由图5(b)减速度呈现为直角三角形状,分布于[0,6.0]m/s2,并且减速度随着行驶车速的增加逐渐递减,体现为实际运行情况下城市道路的制动减速度主要由前车的速度变化所致。

由图5(c)可以看出,各加速度分位值整体都在[0,1.4]m/s2,其折线趋势呈现M形,且均在15～20 km/h上方达到第1个峰值,在30～40 km/h上方达到第2个峰值,随后急剧下降,可能的原因是驾驶人驶入合流区时行车空间较为充足,能缓慢加速行驶,随着车间距的减小,为防止追尾事故发生,加速幅度也随之减小,随着前方车辆驶出合流区,后方车辆再次获得较为充足的行车空间,驾驶人迅速做出反应采取急加速行为以求迅速通过,随后行车空间再次减小,导致加速幅度减小。

图5(d)为减速度的特征分位值折线,其整体分布于[0,4.0]m/s2,各折线图均呈现出明显的上升趋势,即随着初速度的增大,减速度随之增大,可能的原因是当驾驶人以较高车速驶入合流区时,驾驶人期望安全汇入合流区,加之合流区的行车状况并非十分畅通,导致驾驶人踩刹车踏板的力度和幅度较大,从而导致较大幅值的减速度;在50～60 km/h达到减速度分位值峰值,是由落在该分组的数据偏少,并伴随一些异常值所致。

3.2 多元线性回归模型

根据上述高峰时段合流区加(减)速度与车速之间的关系分析,以行驶车速为因变量,初速度v0(t)、加(减)速度a(t)为自变量,构建合流区车辆运行车速预测模型的一般形式,即

v(t)=β0+β1v0(t)+β2a(t)

(2)

式中:β0为常量;β1、β2为模型参数。

多元线性回归统计结果如表2所示。可以看出,回归参数的置信水平均小于0.05,置信度达到95%,VF值均小于5,表明自变量间不存在多重共线性;德宾-沃森值在2附近,表明变量间不存在序列相关;此外,回归标准化残差的变量累积比例与指定分布累积比例关系如图6所示。可以看出,各点的分布贴近对角线,即残差符合正态分布;R2=0.798,满足回归分析的基本条件。

表2 多元线性回归预测模型描述统计Table 2 Descriptive statistics of multiple linear regression forecasting model

图6 回归标准化残差的正态PPFig.6 Normal PP plot of the regression standardized residuals

因此,可得出高峰状态下实例合流区运行车速预测模型,即

v(t)=1.481+0.817v0(t)-0.159a(t)

(3)

4 模型验证

4.1 精度评价指标选取

为评估模型的预测性能,借助拟合优度(R2)、误差均值(Error Mean)、误差的标准差(Error StD)、均方误差(mean squared error,MSE)、均方根误差(root mean square error,RMSE)、归一化均方根误差(normalized root mean squared error,NRMSE)、秩相关(rs)评价指标,建立多指标融合的评价方案[18]。其中R2和rs值用于判断预测车速分布与实际车速分布之间的关联程度,越接近于1,表明预测车速与实际车速之间拟合程度越好; Error Mean及Error StD用于评价误差的整体水平以及误差的离散程度;MSE、RMSE、NRMSE用于评价预测精度,其值越小,表示预测精度越高。

4.2 模型效果分析

采用滑动时窗的方法提取时间步长为1 s的车速序列平均值,对其进行最大最小值标准化方法处理[18],输入至车速估计模型。

(4)

式中:xi为第i个原始数据;x′i为标准化处理后的新数据。

统计模型的预测车速数据,整体来看,多元线性回归车速估计模型表现出较好的预测精度,各指标均优于文献[5]结果,如表3所示。可以看出,拟合程度指标方面R2和rs,分别为79.80%、84.40%,即模型预测值与原始值的相关性高,车速预测结果基本接近实际。匹配程度指标方面,Error Mean、NRMSE分别为0.001 7、0.269 0,Error StD、MSE、RMSE分别为1.659 5、2.754 2、1.659 6,表明模型性能稳定,表现出较好的鲁棒性,本文构建的车速状态估计模型精度满足要求。