基于自适应权重融合的深度多视子空间聚类
2023-07-14孙艳丰胡永利
刘 静, 孙艳丰, 胡永利
(北京工业大学信息学部, 北京 100124)
子空间聚类方法[1-5]作为一种有效的无监督学习方法,在数据挖掘、计算机视觉等领域引起了广泛关注。该方法假设将高维数据嵌入在低维子空间中,并可由其描述表示,因此,子空间聚类的主要目标是将一系列样本分割成互不相干的簇,使每个簇内的样本属于同一个子空间[6-7]。近年来,基于自表示的子空间聚类方法[8-10]因其优异的聚类性能备受关注。该方法的主要思想是将数据集自身作为字典使用,利用数据的表示矩阵构建相似矩阵,从而进行聚类任务。基于自表示的子空间聚类方法在图像表示[11]、人脸聚类[12-13]、运动分割[14]、社交网络中的社区聚类、生物信息学[15]、医学图像分析[16]等方面具有广泛应用。
随着多媒体技术迅猛发展以及各种功能摄像机的普及,数据可以以不同形式被收集,从而产生多特征、多摄像角度、多模态等数据,这些数据被统称为多视数据。相较于单一视图采样的数据,对同一事物从不同角度或按不同方式所得到的多视数据拥有更丰富的信息。多视数据不同视图间存在一致性和互补性,一致性可理解为多视数据各视图间具有一致的语义信息,也就是多个视图的表示共享一套标签。互补性是指多视数据的多个视图之间信息互补,这些信息是每个视图独有的特征,这些特征从不同的角度描述了该数据。因此,结合一致性和互补性可提升人们对多视数据的理解。有效利用这些信息可以克服光照变化、遮挡等问题,有助于提高聚类性能。
多视子空间聚类旨在合并多视数据的特征以将相似的多视样本分到相同的簇中,而将差异较大的多视样本分到不同簇中。Zhang等[13]通过对多视特征的张量表示施加低秩约束来获取不同视图的一致性信息,将张量的低秩约束分解为多个矩阵的低秩约束。Zhang等[17]在多视子空间聚类方法中引入级联的思想,提出潜在多视子空间聚类方法。首先,用多个投影矩阵将不同视图数据投影到相同的低维空间以获得多视数据的公共表示,并处理样本中存在的噪声;然后,将具有公共信息的表示矩阵用于聚类任务。Wang等[18]提出一种能够融合多视间的一致性信息和互补性信息的多视子空间聚类模型,利用互补约束项挖掘不同视图的互补信息,与此同时,利用一致约束项挖掘不同视图的一致信息。虽然上述方法存在显著差异,但是它们均运用一致性原则或互补性原则来确保多视子空间聚类任务的成功。总体而言,通过探索不同视图之间的一致性和互补性,使得多视聚类比单视聚类更加有效且更具泛化能力,这使得多视聚类[19-21]在聚类任务中占据一席之地。
近几年,关于子空间聚类的研究主要关注线性子空间的聚类,然而,实际中的数据不一定符合线性子空间聚类模型假设。例如:人脸图像会受到反射率以及被拍摄者姿态等影响,在这些外部因素影响下,面部图像往往位于一个非线性子空间中。因此,利用深度神经网络结构以一种无监督的方式来学习数据的非线性映射,从而使其更好地适用于子空间聚类是有必要的。深度学习的发展将多视子空间聚类带入了新的阶段,Abavisani等[22]除了提出基于空间融合的各种方法之外,还提出一种基于相似性融合的网络(将与不同模态相对应的自表示层强制设置为相同),使得聚类性能获得显著提升。Zhu等[23]提出了一种多视深度子空间聚类网络,该网络由2个子网组成,即分集网络和通用网络。分集网络学习视图特有的表示矩阵,而通用网络则为所有视图学习一个公共的表示矩阵。通过分集正则项利用多视图表示的互补性,可以捕获非线性和高阶视图间的关系。不同的视图共享相同的标签空间,因此,每个视图的表示矩阵都通过通用性正则项与公共视图对齐。
然而,上述方法在为各视图学习一个公共的表示矩阵时均未能甄别不同视图的可靠性。当存在一个不佳的视图数据时,聚类结果可能因此毁坏。因此,在聚类过程中为每一个视图学习一个权重是有必要的。同时,深度多视子空间聚类对将一致性信息与互补性信息相结合的研究还相对匮乏。如何在保证各视图之间一致性的情况下,充分利用不同视图的互补性信息来提高多视聚类性能,是多视聚类的一个重要问题。
综上所述,本文考虑到多视间共享一致性信息与不同视图所具有的内在个性化信息,提出了在获得所有视图的一致性信息基础上强调互补性(个性化)信息的模型,即基于自适应的权重融合深度多视子空间聚类模型(deep multi-view subspace clustering based on adaptive weight fusion,DMSC-AWF)。该模型通过各视图共享同一个自表示层学习一个共享的子空间表示矩阵,同时,又为各视图分别学习各自的自表示层来确保互补性信息。同时,为了避免某视图出现不可靠的信息从而影响最终聚类效果,引入注意力模块来量化不同视图的重要性,注意力模块自适应地为每种模态分配权重。注意力模块的使用为相似度融合质量提供了鲁棒性保障,从而提升了聚类性能。
1 方法
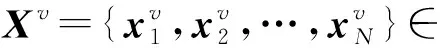
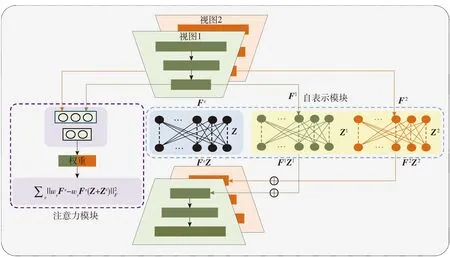
图1 DMSC-AWF网络框架Fig.1 Framework of DMSC-AWF
1.1 注意力模块
深度多模态聚类作为基于多视学习的无监督子空间聚类方法,具有优异的聚类性能。然而,对某些视图数据进行采集时可能存在噪声干扰,会出现数据不可靠的情况,直接进行视图间融合会降低生成的相似度矩阵的有效性。针对这一问题,通过引入注意力模块为各视图自适应地分配融合权重。对于信息量损坏的视图,网络并不撤销对这些信息的注意力,而是降低对其分配的权重。相反,网络也能在训练过程中增加对干净视图的注意力。注意力模块的权重均由网络学习得出,不需要人为指定权重大小,这也符合本文为不同视图自适应匹配权重的特点。
注意力模块以学习不同视图的权重为目标,本模块的输入为潜在表示Fv(v=1,2,…,V)拼接而成的连接特征F,其输出是V维向量w。通常,它由3个全连接层和1个Softmax层组成,通过求平均函数获得输出权重w。注意力模块详细网络结构见图2。

图2 注意力模块结构Fig.2 Structure of attention module
本文使用公式
F=concat(F1,F2,…,FV)
(1)
h=FCs(F)
(2)
e=Softmax(Sigmoid(h)/τ)
(3)
w=Mean(e,dim=0)
(4)
描述该过程。式中:concat(·)表示连接运算符;FCs(·)表示3个全连接的层;h、e为隐含特征;τ为校准因子;Sigmoid函数与校准因子τ可以看作是一种技巧,用来避免为质量最优的视图分配接近1的分数;Mean(e,dim=0)表示对e每一列求平均值。为了简单起见,将该模块中的参数表示为Θa。
1.2 自表示模块
因为对于深度多模态聚类缺乏对互补性信息的研究,所以本文在深度子空间网络的自表示层进行改进。传统的模型假设各视图共享学习一个公共的自表示层,自表示模块的输入为各视图的潜在表示Fv,输出为经自表示的潜在表示FvZ,Z为公共自表示层系数,即公共表示矩阵,同时FvZ也将作为后续解码操作的输入,这种传统自表示模型可以用
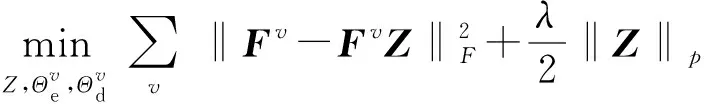
(5)

本模块为传统自表示模型增加了视图特定的自表示层,结构上本模块的输入仍是各视图的潜在表示Fv,而输出除了经公共自表示层自表示的潜在表示FvZ,还增加了FvZv。因此,本模块可以分为一致性模块和互补性模块。解码器的输入变成了FvZ与FvZv之和,在数学上,模型可以表示为
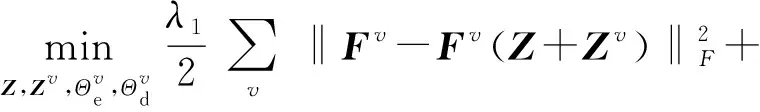
(6)
式中Zv为各视图特定的自表示层系数,即个性表示矩阵,此处同样要求Zv对角线元素为0。
最后,本文用网络收敛后学习到的公共表示矩阵Z构建相似度矩阵A(A=(|Z|+|ZT|)/2),对A执行谱聚类。
1.3 损失函数
由于多视数据各视图之间既有一致性又有互补性,通常用约束各视图的个性表示矩阵与公共表示矩阵距离相近来约束各视图一致性。Cao等[12]考虑到视图间信息多样性,引入希尔伯特-施密特独立性准则(Hilbert-Schmidt independence criterion,HSIC)[12,24]来学习多视图间的互补性信息,如RGB信息和深度信息,主要目的是衡量2个变量的分布差异,因此,可以度量非线性和高阶相关性。在此基础上,将互补性正则化Rs定义为
(7)
式中Zi和Zj分别表示第i个和第j个视图对应的视特定表示矩阵。
式(7)利用HSIC确保学到的各视图的个性表示矩阵具有足够的差异性,从而达到有效利用来自多个视图的互补信息的目的。
所有视图共享相同标签,因此,各视图特定表示矩阵应该与公共表示矩阵对齐。本文将一致性正则化Rc定义为
(8)
结合注意力模块和自表示模块的权重和约束,基于权重融合的多视子空间聚类模型,最终可以表示为
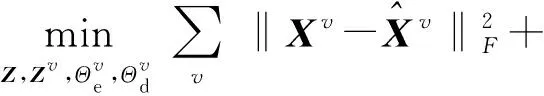
(9)
式中:Xv为模型输入数据,v代表第v个视图;v为重构数据;λ1、λ2、λ3、λ4为正则化项系数。式(9)第1项表示重构损失;第2~4项表示带权重的自表示损失及其正则项;第5项表示一致性正则项,约束各视图个性表示矩阵向公共表示矩阵逼近;第6项表示互补性正则项保证视特定表示矩阵相互独立,确保模型可以充分挖掘多视信息的多样性。DMSC-AWF模型的详细学习过程在算法1中给出。


2 实验结果
为验证本模型的有效性,本文进行了大量实验,包括聚类实验,注意力模块、互补性模块退化实验和具有噪声数据的实验等,并将其与近年来的几种方法进行比较,以验证所提出模型的性能。此外,对实验中使用的数据集、对比方法、参数设置进行了详细说明。本文实验将相似度矩阵A=(|Z|+|ZT|)/2用于4个多视数据集以实现聚类任务。
本文方法使用Python 3.7环境及采用Tensorflow框架编码,操作系统为Linux,显卡为RTX 2080S×2,显存为8 GB×2。
2.1 对比方法与数据集
在聚类实验中,将本文提出的DMSC-AWF与近年来性能较为优异的子空间聚类算法进行比较。对比方法包括单视传统子空间聚类算法和深度子空间聚类算法,共4种。
1) 基于低秩表示的子空间结构鲁棒恢复(robust recovery of subspace structures by low-rank representation,LRR)[11]。在所有候选中寻求最低秩表示,这些候选可以将数据样本表示为给定字典中具有最佳单视图的基的线性组合。
2) 深度子空间聚类网络(deep subspace clustering networks,DSCN)[25]。该算法将通过原始数据计算出的稀疏表示矩阵作为先验知识,再结合自编码器网络将原始数据映射到潜在空间。该模型首次将子空间聚类用于深度自编码器框架。
3) 对子空间聚类的深度认知(deep cognitive subspace clustering,DCSC)[26]。该算法对损失施加一个自定速正则化,是一种鲁棒的深度子空间聚类算法。
4) 无监督学习视觉特征的深度聚类(deep clustering for unsupervised learning of visual features,DC)[27]。该算法使用k-means在聚类之间迭代,并通过将聚类分配预测为伪标签来更新其权值,从而产生判别损失,是一种可扩展的无监督聚类方法。
对比方法包括多视传统子空间聚类算法和深度子空间聚类算法,共5种。
1) 共同规范化多视谱聚类(co-regularized multi-view spectral clustering,Co-Reg SPC)[28]。该算法通过谱聚类目标函数隐式结合多个视图的图形,并进行聚类,以实现更好的聚类结果。
2) 通过低秩稀疏分解实现鲁棒的多视谱聚类(robust multi-view spectral clustering via low-rank and sparse decomposition,RMSC)[29]。为解决无甄别结合含有噪声的多视数据影响聚类结果的问题,该模型为单视图构造相应转移概率矩阵,并通过这些矩阵获得一个共享的低秩转移概率矩阵,并将其作为标准马尔可夫链聚类方法的关键输入,该模型具有低秩和稀疏性。
3) 通过深度矩阵分解进行多视聚类(multi-view clustering via deep matrix factorization,DMF)[30]。该算法通过半非负矩阵分解学习多视数据的多层次语义信息。
4) 潜在的多视子空间聚类(latent multi-view subspace clustering,LMSC)[17]。该算法寻找原始数据的潜在表示,同时,根据学习到的潜在表示进行数据重构。
5) 深度多模态子空间聚类(deep multimodal subspace clustering networks,MSCN)[22]。研究发现,该模型在深度多模态子空间聚类任务中的空间融合方法依赖于模式之间的空间对应。
为评估提出的基于权重融合的多视子空间聚类恢复算法性能,本研究在4个公共数据集上进行了大量实验,数据集简介如下。
1) ORL人脸数据集[31]。该数据集包含40个人的10张不同的图像。对于每个受试者,图像采集时的控制光照条件、面部表情和面部细节不同。对于ORL原始数据集,本实验调整图像大小为48×48,提取3种类型的特征,即强度(4 096维)、局部二值模式(local binary pattern,LBP)(3 304维)和Gabor(6 750维)。标准的LBP特征是从72×80像素的图像中提取的,直方图大小为59~910个像素块。Gabor特征是在4个方向θ=0°、45°、90°、135°的情况下以同一个尺度λ=4提取的,其分辨率为25×30像素的松散脸部裁剪。除了强度之外,所有描述符都缩放为单位范数。
2) Still DB数据集[23]。该数据集由467张行为动作图像构成,主要包括6类:跑步、行走、接球、投掷、蹲下、蹋腿。由于行为动作姿势的相似和图片有杂乱的背景,该数据集是具有挑战性的行为图像数据库。
3) BBC Sport数据集[32]。该数据集包含544份来自BBC体育网站的体育新闻文章,这些文章在2004、2005年涉及5个主题领域的2个视图。对于每个示例,第1个视图有3 183个特征,第2个视图有3 203个特征。BBC Sport的部分子集如图3所示。
图3 BBC Sport文本数据集的部分原始样本Fig.3 Part of the original sample of the BBC Sport text dataset
4) RGB-D对象数据集[33]。该数据集包含从多个视图中获取的300个物理上(传感器距离物体的实际距离)截然不同的对象的视觉和深度图像,这些对象按照WordNet上下名关系(类似于ImageNet)被组织成51个类别。本实验中随机选择50个类,每类10个样本。所有视觉图像和深度图像大小均为64×64像素。实验中使用递归中值滤波,直到所有缺失的值都被填满。RGB图像和深度图像的子集如图4所示。

图4 RGB-D对象数据集的部分样本Fig.4 Part of sample from the RGB-D object dataset
4个公开数据集ORL、Still DB、BBC Sport和 RGB-D在本文实验中的使用情况如表1所示。

表1 数据集情况统计Table 1 Statistics of datasets
2.2 参数设置与评估指标
本文模型使用[64,32,16]通道的3层编码器,相应地使用[16,32,64]通道的3层解码器。卷积层的卷积核大小都设置为3×3,而非线性激活函数为整流线性单元。然后,通过反卷积层将潜在特征返回到与输入大小相同的空间。同时,在所有实验中将lr设置为0.001。以RGB-D数据集为例,其输入为2个视图数据:一个视图数据为彩色视觉图像(有3个通道),另一个视图数据为深度图像(有1个通道)。2个视图的通道分别为3—64—32—16—32—64—3和1—64—32—16—32—64—1。横向和纵向平移步长为2,填充方式为same,迭代次数为40,λ1=1.00,λ2=1.00,λ3=0.10,λ4=0.10,τ=0.50。为确定上述关键参数(λ1、λ2、λ3、λ4、τ)取值对聚类性能的影响,本文固定其他4个参数,依次分析各参数对聚类性能的影响。不同参数在RGB-D数据集的DMSC-AWF性能见图5。图5(a)~(d)中λ1、λ2、λ3、λ4的取值范围设置为[0.01,0.10,1.00,10.00,100.00]。结果表明,当λ1、λ2被设为1.00时,本文方法在不同的性能指标上均有良好的表现。同样,可以观察到,当λ3、λ4设为0.10时,本文提出的DMSC-AWF具有更好的性能。当τ分别取0.1、0.5、1.0、10.0、20.0时进行实验,当τ=0.5时效果最优。

图5 不同参数对DMSC-AWF性能的影响Fig.5 Effect of different parameters on DMSC-AWF performance
本实验使用4个流行的评价指标来评估聚类效果,包括准确度(accuracy,ACC)ACC、归一化互信息(normalized mutual information,NMI)NMI、精确率和召回率的加权调和平均Fmeasure和可以综合评价性能的调整兰德指数(adjusted Rand index,ARI)IAR。其中,分数越高,表示聚类性能越好。
ACC的计算公式为
(10)
式中:li为真实标签;yi为模型产生的聚类结果;m(yi)为置换映射函数,将聚类标签映射到类标签;n为样本数。置换映射函数的最佳映射可通过匈牙利算法获得。
NMI是数据真实标签l和聚类标签k之间相似度的归一化度量,计算公式为
(11)
式中:I(l;y)表示l和y之间的互信息;H(l)、H(y)分别表示l和y的熵。NMI的结果不因簇(类)的排列而改变,它们归一化为[0,1],0表示没有相关性,1表示完全相关。
IAR反映聚类标签与数据真实标签的重叠程度,具体计算公式见文献[34]。
Fmeasure常用于衡量模型的有效性,取值范围为[0,1],公式为
(12)
式中:P为精确率;R为召回率。
2.3 实验结果对比与分析
实验时,将MSCN与本模型DMSC-AWF的迭代步数保持一致,并以最后一次迭代的结果作为最终结果。其他对比实验结果取自文献[23]。在实验设置中,所有方法都使用k-means聚类方法来得到最终的聚类结果。解的初始化严重影响k-means的性能,因此,实验时把每个代码均运行30次,并给出了平均性能和标准偏差。为验证本模型及本模型提出的各个模块的有效性,分别进行了聚类实验、退化实验以及具有噪声实验。
2.3.1 聚类实验
为验证本文模型的有效性,本实验将不同方法在ORL、Still DB、BBC Sport和RGB-D数据集上的聚类结果进行对比,实验结果如表2~5所示。表中黑体数字为最佳结果。
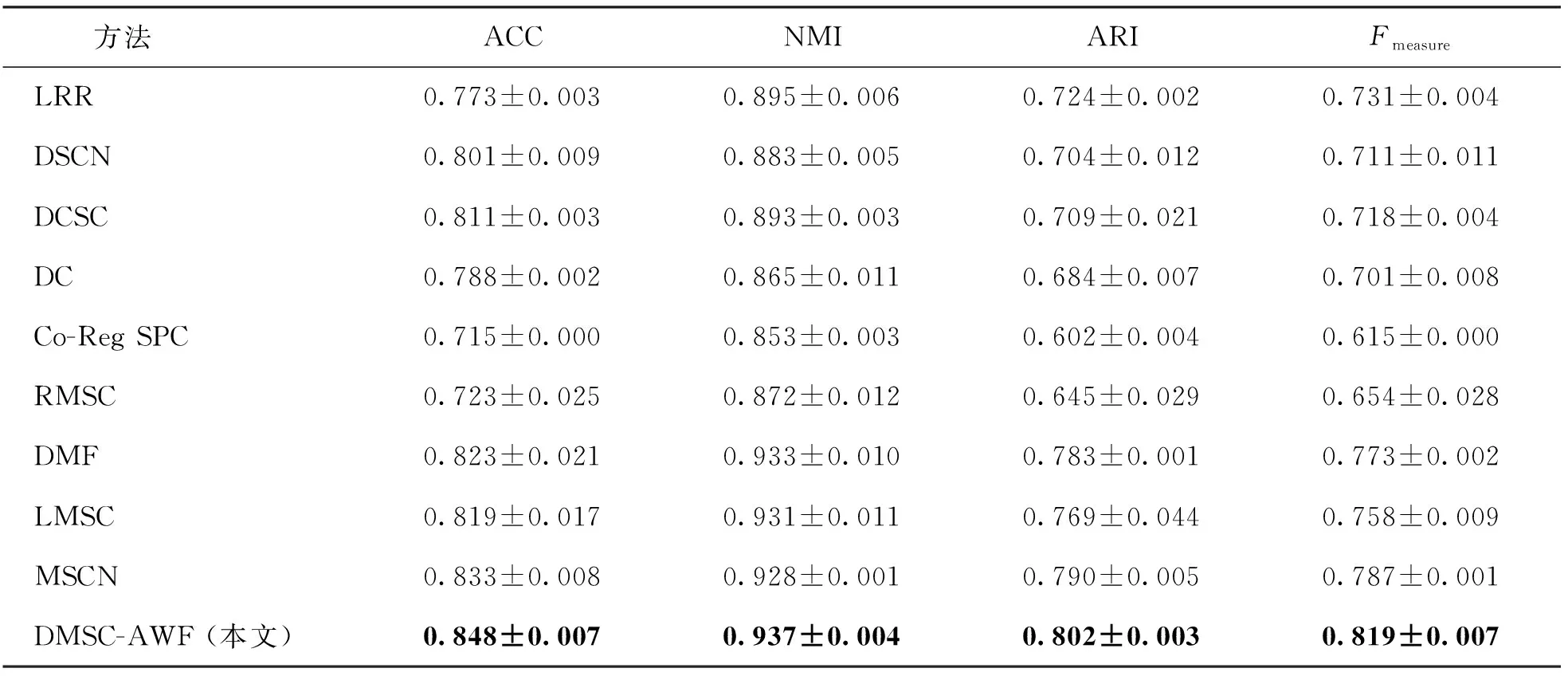
表2 不同方法在ORL下的聚类性能对比Table 2 Comparison of the clustering performance of different methods under the ORL dataset

表3 不同方法在Still DB下的聚类性能对比Table 3 Comparison of the clustering performance of different methods under the Still DB dataset
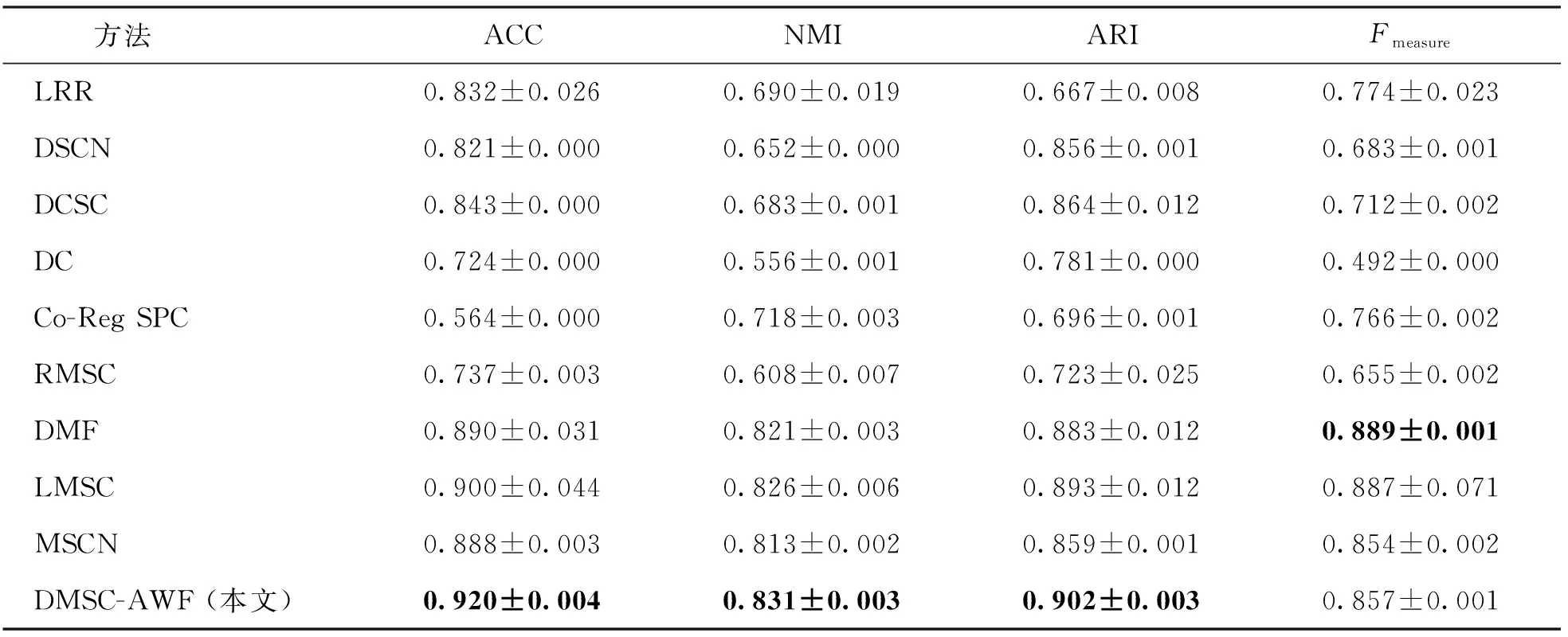
表4 不同方法在BBC Sport下的聚类性能对比Table 4 Comparison of the clustering performance of different methods under the BBC Sport dataset

表5 不同方法在RGB-D下的聚类性能对比Table 5 Comparison of the clustering performance of different methods under the RGB-D dataset
根据聚类结果显示,本文提出的方法在ORL、Still DB、BBC Sport和RGB-D数据集上明显优于其他对比方法的聚类性能。例如:对于RGB-D来说,本文提出的模型ACC提高了4.3%,NMI提高了2.0%,ARI提高了0.8%,Fmeasure提高了1.4%。这证明了所提出的DMSC-AWF模型在多视子空间聚类任务中的有效性。同时,在聚类结果中可以看出:1) 无论是单视还是多视,使用深度网络的方法相比于传统方法具有较高的准确度,这表明深度网络具有更好地提取非线性数据特征的能力,有助于提高聚类效果。2) 在同样使用深度网络的情况下,多视聚类方法相较于单视聚类方法取得了更好的聚类性能,这表明有效利用多视角数据,在大多数情况下可以获得较为不错的聚类性能。
综上可知,性能的提升主要体现在3个方面:一是在网络中以端到端的方式学习相似度矩阵;二是将多视数据的一致性信息和互补性信息结合,并应用到自表示中;三是做相似度融合时将注意力模块应用到网络中,为不同质量的视图数据分配合适的权重。
2.3.2 注意力模块及互补性模块退化实验
为验证本文提出的模块的有效性,以RGB-D数据集为例,对包含添加了互补性信息的自表示模块和注意力模块的模型DMSC-AWF、在DMSC-AWF模型基础上去掉注意力模块的模型DMSC-AWF/att以及在DMSC-AWF/att模型基础上去掉互补性模块的MSCN模型进行实验,最终聚类结果见表6。

表6 退化实验的聚类性能对比Table 6 Clustering performance of degraded experiments
由表6可以看出,DMSC-AWF相较MSCN和DMSC-AWF/att具有较为优异的性能优势。因为DMSC-AWF/att与MSCN的区别在于DMSC-AWF/att的自表示模块中包含互补性模块,所以由DMSC-AWF/att与MSCN的实验结果可知,在自表示模块中添加互补性模块是非常有必要的。DMSC-AWF在聚类性能上大致高于没有添加注意力模块的DMSC-AWF/att,同时,DMSC-AWF聚类结果的标准差小于DMSC-AWF/att,这说明添加注意力模块有助于提高网络的鲁棒性,从而提升聚类稳定性。本退化实验结果证实了注意力模块及互补性模块的有效性。
2.3.3 具有噪声数据的聚类实验
以RGB-D数据集为例,在本数据集的某一视图上添加高斯噪声,从而获得一组新的噪声数据。将这组噪声数据作为一个视图同另一个视图一起送入网络中,并将本模型DMSC-AWF与MSCN的聚类结果进行对比。将高斯噪声均值设置为0,标准差设置为0.2。在本部分预训练实验中一个视图的输入数据为噪声数据。具有噪声数据的聚类结果如表7所示。表中黑体数字为最佳结果。

表7 标准差为0.2的噪声数据的聚类性能Table 7 Clustering performance of noise data with standard deviation of 0.2
根据表7中展示的添加噪声实验的聚类结果可以看出,如果原始图像包含噪声,则会降低聚类性能,但本文提出的方法依旧可以保持一个不错的聚类效果。相比于MSCN来说,本文模型ACC提高了3.8%,NMI提高了0.5%,ARI提高了1.7%,Fmeasure提高了1.7%。为进一步直观体现本模型面对噪声数据的鲁棒性,本文对不同视图的权重进行了可视化,展示了有噪声的视图和无噪声的视图之间的权重差异,实验结果如图6所示。本噪声实验验证了在面对不可靠数据时,本文提出的基于权重融合的方法相对于各视图直接融合的传统方法具有更强的鲁棒性,从而证实了融合时对各视图分配不同权重是有必要的。
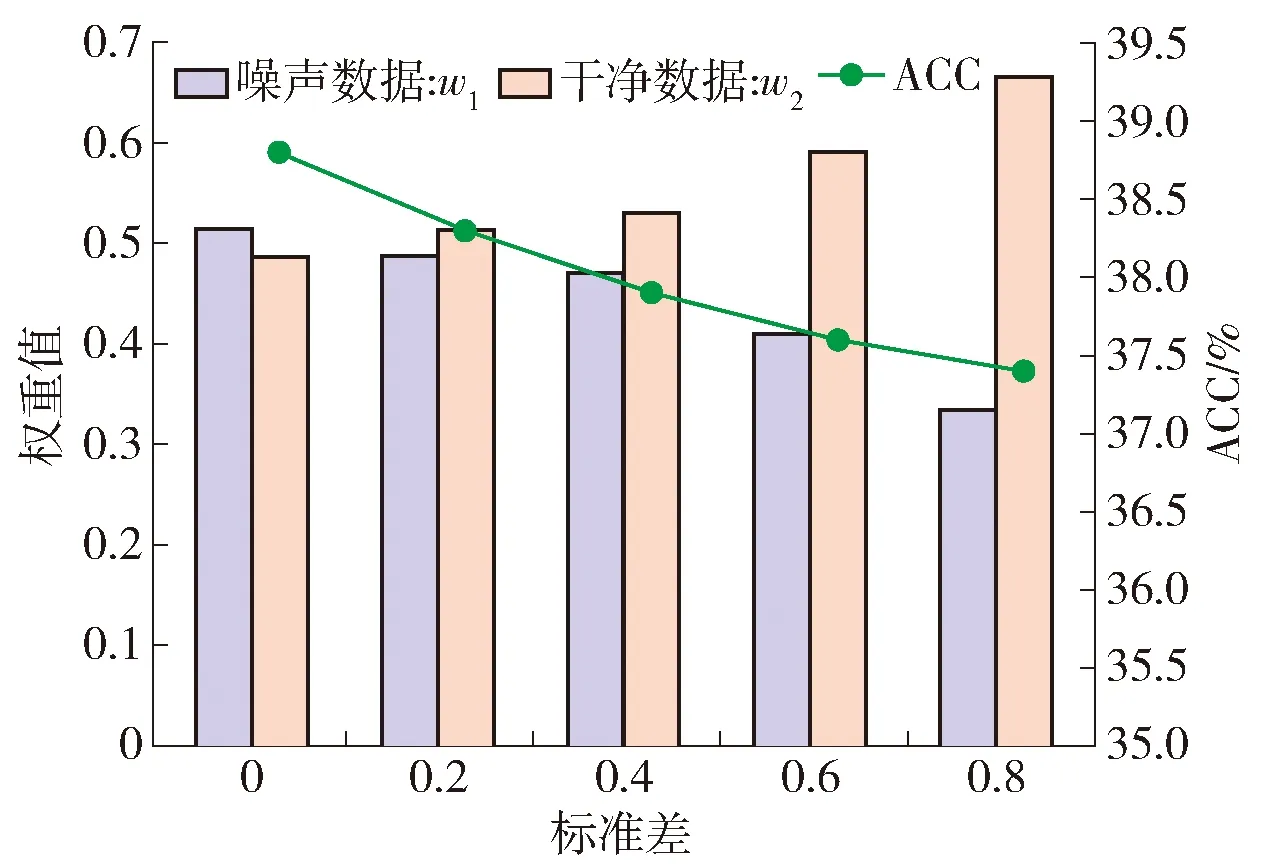
图6 对噪声实验权重可视化Fig.6 Visualization of experimental weight of noise
3 结论
1) DMSC-AWF方法强制各视图共享自表示层(相似度融合)以确保一致性,并在此基础上强调了各视图独立的互补性信息,即为各视图分别学习一个自表示层。同时,在多视信息融合时利用注意力模块学习到各视图的权重分配,为相似度融合质量提供了鲁棒性保障。
2) DMSC-AWF算法可以提升数据融合质量,从而提升聚类性能。
3) DMSC-AWF的注意力模块有助于提高网络的鲁棒性,使网络具有一定抗噪声能力,从而提升聚类稳定性。
