单自由度主动磁悬浮轴承-转子系统输入时滞稳定性研究

金超武 ，马彦超，周瑾，徐园平，叶周铖

（南京航空航天大学 机电学院，江苏 南京 210016）

主动磁悬浮轴承（Active Magnetic Bearing，AMB）利用可控电磁力将转子悬浮在设定的工作位置，因其具有无机械接触、高转速、低功耗、可在线检测以及可主动控制等优点而得以在压缩机、膨胀机等高速旋转机械中广泛应用［1］.当用于控制与驱动AMB 的电子设备对环境比较敏感，需将相关电子设备与磁悬浮轴承本体进行分离时（例如深海钻井平台、风力发电等应用场所），由于控制系统与执行单元的分布设置，控制回路中的时滞量进一步增加，这将导致系统内的时滞问题更加凸显［2］，严重时甚至导致系统失稳.在主动磁悬浮轴承-转子系统中，控制器内控制算法运算执行、信号在功率放大器电路中的传导转换等因素的存在，使得输入磁悬浮轴承的控制电流内存在一定的时滞，该时滞称为控制器输入时滞［3］（后文简称输入时滞）.在输入时滞的影响下，主动磁悬浮轴承-转子系统将表现出复杂的动力学行为，如周期、拟周期以及混沌等形式［4］，并且随着转速的提高以及对系统动力学行为的研究要求越来越精细，有关时滞对系统影响的研究显得愈发迫切.

近30 年来，针对主动磁悬浮轴承-转子系统中的时滞问题，众多学者对此进行了许多突破性的研究，为研究系统时滞问题采用各类数值分析方法，提供强有力的分析工具.为了分析时滞系统的动力学特性，Ruan 等［5］利用特征值法对Hopf 分岔的分岔方向、振幅以及周期等方面进行了研究，并概括了切实可行的计算公式.在此基础上，Wang 等［6］对特征方程的一些临界情况，例如零点为单根或双根等进行了讨论，并研究了在上述情况下不动点的稳定性和零解附近的动力学问题.利用所得的基本定理，可以很好地判断该类磁悬浮轴承系统Hopf分岔的存在性以及平衡点的渐近稳定性.Xu 等［7］将具有时滞的主动磁悬浮轴承-转子系统作为研究对象，对系统的稳定性和分岔存在情况进行了研究，并进行了动力学方面的分析.王珍［8］研究了一类具时滞的磁悬浮系统模型，对系统平衡点的稳定性和Hopf 分岔等进行了分析，并研究了系统时滞量、比例增益以及微分增益等参数对系统动力学性质的影响规律.Su 等［9］对基于PD 控制的AMB 系统的时滞问题进行了研究，讨论了系统时滞对磁悬浮轴承系统的影响，推导了引起系统不稳定的最大延迟时间的显式公式和数值解，并给出了单自由度AMB 系统时滞效应的数值模拟结果.郑凯等［10-11］对AMB 系统进行了时滞动力学建模，发现即使是控制反馈回路中的微小时滞也会对高速转子系统的稳定性产生重大影响.Li 等［12］利用数值方法研究了速度反馈控制回路的时滞对单自由度AMB 系统强迫振动的影响，验证了时滞增加将使稳定周期运动的幅度增大，系统可能会出现失控现象.

上述研究表明，时滞将影响主动磁悬浮轴承-转子系统的性能及稳定性.但是，当前对于主动磁悬浮轴承-转子系统的时滞研究主要存在两大局限性：①大多是从单一角度研究时滞对主动磁悬浮轴承-转子系统的影响，未从多角度进行体系化的研究；②大多集中在理论研究层面，试验研究匮乏.

针对上述局限性，本文对基于PID 控制的主动磁悬浮轴承-转子系统的输入时滞问题开展研究，从控制器参数、Hopf分岔以及闭环系统幅频、相频特性等多个角度研究输入时滞对系统稳定性的影响，并进行了相关仿真与实验.通过对输入时滞系统稳定性进行多角度的分析，为实际工程应用中的控制器参数调试提供指导，降低输入时滞对系统稳定性的影响.

1 理论分析

1.1 主动磁悬浮轴承-转子系统临界时滞

图1 为具有输入时滞的AMB-转子系统等效模型，主要包含控制器、功率放大器、电磁铁-转子以及位移传感器等.

图1 具有输入时滞的AMB-转子系统等效模型Fig.1 Equivalent model of AMB-rotor control system with input time delay

将输入时滞引入系统后，该系统的运动微分方程可表示为：

式中：m为转子质量；x（t）为转子位移；τ为输入时滞；ix为控制电流；kx、ki分别表示AMB 的位移刚度和电流刚度.ix（t）可进一步表示为：

式中：ks为位移传感器增益；ka为功率放大器增益；kP、kI以及kD分别表示PID 控制器的比例增益、积分增益以及微分增益.联立式（1）和式（2）进行拉普拉斯变换，得到系统特征方程为：

当τ值较小时，基于等价无穷小原理，将式（3）中的e-τs替换为1-τs后，可进一步得：

由劳斯方程可知，系统稳定的充要条件是其特征方程的全部系数及劳斯表的第一列元素均为正数.因此可以得到不等式组：

对式（5）求解得：

值得注意的是，由于在式（4）中采用了近似替换，本节后续推导得到的临界时滞为近似值.基于式（6）可知，系统临界时滞的近似值τ临=min（τ1，τ2，τ3，τ4）.

1.2 Hopf分岔

时滞常使系统出现各种形式的分岔及混沌运动，而Hopf 分岔点是系统由定常状态通向复杂动力学状态的门槛，所以Hopf 分岔的研究最为广泛.Hopf 分岔是指参数在变化过程中经过分岔值τ0时，系统由定点稳定性突变产生极限环的现象，也是一种重要的动态分岔现象，如图2 所示.初始状态稳定的系统在发生Hopf 分岔时，其特征值的实部由负经分岔值（特征值实部为0）变为正，系统平衡点的稳定性将发生变化.Hopf 分岔发生时处于稳定与失稳之间的临界稳定状态，此时系统的稳定运行将无法得到保证.Hopf 分岔是时滞在恶化系统稳定性时所表现出来的重要的动力学特征，同时亦是众多学者对于时滞问题的研究重点.因此，在研究时滞系统的稳定性时，有必要对Hopf分岔进行研究.

图2 Hopf分岔过程Fig.2 Hopf bifurcation process

Hopf 分岔存在时要满足两个重要的条件：一是系统在特定参数下存在一对共轭纯虚根；二是满足横截条件，即根轨迹穿越虚轴时速度不为0，换言之，根轨迹在穿越虚轴时特征值实部的导数不为0［13］.

1.2.1 Hopf分岔的存在性分析

假设系统特征方程存在一对共轭纯虚根，记为s=iω（ω=±α，α＞0），将其代入式（3），得

联立欧拉公式eix=cosx+i sinx，并分离实部、虚部后得到方程组：

式中：

将式（8）中两式的两边同时平方再相加，得

由于sin2(τω)+cos2(τω)=1，与式（8）联立，并令t=ω2（t＞0），得

式中：a=-2q-d2；b=q2-p2+2dr；c=-r2.

因此，系统特征方程存在一对共轭纯虚根等价于式（10），存在正实根.由于

由零点存在性定理可知，式（10）至少存在一个正实根t0，相应地系统特征方程至少存在一对共轭纯虚根，此时系统内的输入时滞记为τ0.

1.2.2 横截条件的满足性分析

要证明该系统满足横截条件，即根轨迹穿越虚轴时速度不为0，只要考虑根轨迹在穿越虚轴时特征值实部的导数不为0，即证明.本节讨论的成立条件.

联立式（3）和式（12）得：

将τ=τ0，s=iω代入式（13），并求实部，得

2 仿真分析

2.1 Hopf分岔存在性数值仿真

结合1.1 节和1.2.1 节的分析可知，系统特征方程存在一对共轭纯虚根.表1为AMB-转子系统主要参数.PID 控制器的kP=2.2、kI=1、kD=0.001 5，通过对式（6）～式（15）进行计算，得τ临、τ0、ω的理论近似值分别为0.681 ms、0.646 ms、592 rad/s.由此得到Hopf分岔对应频率为：

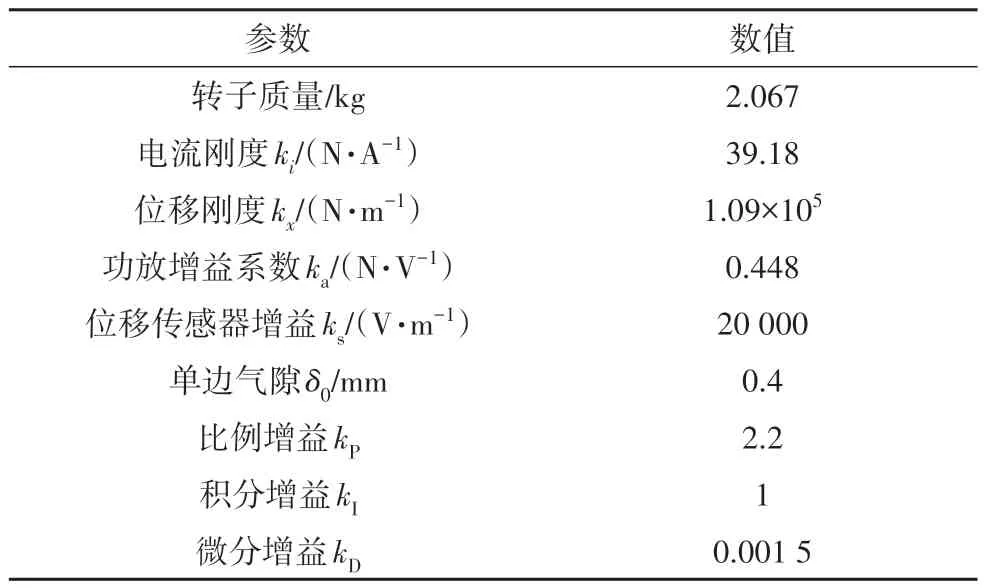
表1 AMB-转子系统主要参数Tab.1 Main parameters of AMB-rotor system

在某一确定参数τ下，系统特征值存在一对共轭纯虚根且满足横截条件.因此，系统将发生Hopf分岔.

本节以前文中理论分析为指导，对Hopf 分岔的存在性进行数值仿真，Hopf 分岔后极限环幅值随输入时滞的变化曲线如图3 所示.从图3 中可以看出，τ0为0.643～0.644 ms，与理论计算值0.646 ms 非常接近；Hopf分岔发生后，极限环的幅值随着输入时滞的增加而增大.为了清晰地呈现出Hopf 分岔过程，本节分别对τ=0.610 ms（τ＜τ0）、τ=0.644 ms（τ0＜τ＜τ临）以及τ=0.700 ms（τ＞τ临）3 种状态下各自对应的系统相轨迹进行分析.

图3 Hopf分岔后极限环幅值随输入时滞的变化曲线Fig.3 Limit ring amplitude curve with input time delay after Hopf bifurcation

图4 为τ=0.610 ms 时Hopf 分岔前系统相轨迹.由图4可知，当τ＜τ0时，系统最终将收敛至一点，此时系统是稳定的，即1.2 节提到的“定点稳定性”.图5为τ=0.644 ms 时Hopf 分岔时系统的响应.由图5（a）～图5（d）可知，在τ＞τ0且τ＜τ临时，系统发生了Hopf分岔，最终获得了稳定的周期解，并产生了极限环.当系统初始时刻位于极限环内部时，相轨迹将由内向外逐渐接近极限环；反之，相轨迹将由外向内逐渐接近极限环.由图5（e）可知，当系统发生Hopf 分岔时，频谱主要包含极限环运行频率对应谱线，即94 Hz的主频谱线，该频率与理论计算值几乎一致.此外，频谱图中还包含主频的倍频谱线，此处主要为主频的3倍频谱线.

图4 τ=0.610 ms时Hopf分岔前系统相轨迹Fig.4 System trajectory before Hopf bifurcation at τ=0.610 ms

图5 τ=0.644 ms时Hopf分岔时系统的响应Fig.5 Response of system when Hopf bifurcation at τ=0.644 ms

仿真结果表明，当τ＞τ临≈0.681 ms 时，系统相轨迹将发散失稳，但是在τ接近τ临时系统的发散趋势缓慢.为了清晰地呈现相轨迹发散失稳的过程，τ=0.700 ms 时极限环破裂后系统相轨迹，如图6 所示.结合图5（a）～图5（d）和图6可以看出，随着输入时滞的进一步增加，极限环发生破裂，相轨迹发散失稳.

图6 τ=0.700 ms时极限环破裂后系统相轨迹Fig.6 System trajectory after limit ring rupture at τ=0.700 ms

2.2 控制参数对时滞系统稳定性的仿真分析

由式（6）中的τ3、τ4可知，kI主要位于分母，而kx位于分子且其量级较大，弱化了kI对系统临界时滞的影响.因此，本节在满足相关控制参数均可保证实际系统在无时滞干扰下稳定运行的这一条件下，主要分析PID 控制器中比例增益及微分增益对时滞系统稳定性的影响，详细研究了如何通过调整控制参数，提高系统稳定裕度，使系统在工程应用中远离临界稳定区域.

2.2.1 比例增益对时滞系统稳定性的仿真分析

PID 控制器的kI=1、kD=0.001 5、kP分别取2.0、2.2 以及2.4，输入时滞τ从0 变化到0.700 ms，变化步长为0.02，对式（3）求解得到系统的特征根，并绘制出不同kP下系统随τ变化的根轨迹如图7所示.

图7 不同kP下系统随τ变化的根轨迹图Fig.7 Root locus diagram of system over τ at different kP

由图7 可以看出，系统特征值由一实根和一对共轭复根组成，当kP一定时，随着τ的增加，该实根保持不变，而共轭复根发生变化.随着kP的增加，由共轭复根组成的两组特征根逐渐从左半平面靠近虚轴，并最终越过虚轴进入右半平面，导致系统失稳.为了更直观地说明kP变化对时滞系统稳定性的影响，对τ=0.644 ms、kP分别取2.0、2.2 及2.4 时系统相轨迹的变化情况进行分析，如图8所示.

图8 τ=0.644 ms时不同kP下系统的相轨迹对比Fig.8 Phase trajectory comparison of systems under different kPat τ=0.644 ms

从图8 中可以看出，随着kP的增加，系统的相轨迹由内向外逐渐从定点稳定变为稳定周期运动，最后变为发散失稳，更加形象地说明了kP的增加将放大输入时滞对系统稳定性的影响，对时滞系统的稳定性具有阻碍作用.此外，将系统不出现正实部特征根时对应的输入时滞（即临界时滞）定义为该系统的稳定裕度.为了准确地分析系统的稳定裕度，将输入时滞τ调整为0～1.5 ms，kP为1.0～2.5，求解得到不同kP下系统稳定裕度的变化情况，如图9 所示.从图9中可以看出，随着kP的增加，系统的稳定域逐渐收窄.结合式（5）分析可知，随着kP增大，系统的稳定裕度将由不等式τ2决定，此时kP与系统稳定裕度呈反比关系，这表明kP的增加将放大输入时滞对系统稳定性的影响，对时滞系统稳定性起阻碍作用.

图9 kP对时滞系统稳定性的影响Fig.9 Effect of kPon stability of time-delay system

2.2.2 微分增益对时滞系统稳定性的仿真分析

为分析kD对系统稳定性的影响，PID 控制器中kP=2.2、kI=1、kD分别取0.001 0、0.001 5以及0.002 0，τ从0 变化到0.700 ms，变化步长为0.02，对式（3）求解得到系统的特征根，并绘制出不同kD下系统随τ变化的根轨迹，如图10所示.

图10 不同kD下系统随τ变化的根轨迹图Fig.10 Root locus diagram of system over τ at different kD

从图10 中可以看出，当kD一定时，随着τ的增加，该实根保持不变，而共轭复根发生变化.随着kD的增加，由共轭复根组成的两组特征根逐渐从右半平面靠近虚轴，并最终越过虚轴完全进入左半平面，系统由不稳定状态变为稳定状态.为了更直观地说明kD变化对时滞系统稳定性的影响，对τ=0.644 ms、kD分别取0.001 0、0.001 5 及0.002 0 时系统相轨迹的变化情况进行了分析，如图11所示.

图11 τ=0.644 ms时不同kD下系统的相轨迹对比Fig.11 Phase trajectory comparison of systems under different kDat τ=0.644 ms

从图11 中可以看出，随着kD的增加，系统的相轨迹由外向内逐渐从发散失稳变为稳定周期运动，最后变为定点稳定，更加形象地说明了kD的增加有利于提高时滞系统的稳定性.

为了准确地分析系统的稳定裕度，将输入时滞τ调整为0～1.5 ms，kD为0.001～0.002，求解得到不同kD下系统稳定裕度的变化情况，如图12 所示.从图12中可以看出，随着kD的增加，时滞系统的稳定域呈线性增加趋势.结合式（5）分析可知，由于kD值较小，系统的稳定裕度由不等式τ2决定，即kD/kP，kD位于分子，因此，kD与系统的稳定裕度呈线性关系，这也表明适当增加kD将弱化输入时滞对于系统稳定性的影响.

图12 kD对时滞系统稳定性的影响Fig.12 Effect of kDon stability of time-delay system

2.3 输入时滞对闭环系统幅频、相频特性的影响

主动磁悬浮轴承-转子系统是开环不稳定系统，且系统的工作环境复杂，外部存在较多的多源信号干扰.考虑到系统的频率响应可以显示出该动态系统诸如谐振、相移等许多重要性质和特点，因此本节分别对不同输入时滞下的主动磁悬浮轴承-转子闭环系统进行扫频仿真，旨在探究输入时滞对系统幅频特性和相频特性的影响，进而确定输入时滞对闭环系统抑制外部干扰能力的影响规律.主动磁悬浮轴承-转子闭环系统的扫频示意图如图13 所示，通过在闭环系统的输入端叠加正弦扫频信号，即激振信号，使闭环系统内各环节均叠加有与该激振信号同频的信号；而后同时采集输入端的激振信号以及输出端的位移响应信号；最后将采集的信号利用离线快速傅里叶变换处理得到整个主动磁悬浮轴承-转子闭环系统在相应频率下的幅频特性和相频特性.该闭环系统幅频和相频响应随输入时滞变化的曲面图分别如图14和图15所示.

图13 闭环系统的扫频示意图Fig.13 Sweep frequency diagram of closed loop system

图14 闭环系统幅频响应随输入时滞变化的曲面图Fig.14 Surface diagram of amplitude-frequency response of closed-loop system varies with input time delay

图15 闭环系统相频响应随输入时滞变化的曲面图Fig.15 Surface diagram of frequency response of closed loop system varies with input time delay

从图14 可以看出，随着输入时滞的增加，系统谐振频率的峰值显著增大，系统幅频响应曲线的峰化现象加剧，使系统稳定周期运动的幅度增大，反映出系统对外部干扰的反应愈发强烈，同时表明系统的稳定性在此过程中明显恶化.从图15 可以看出，随着输入时滞的增加，相频响应曲线逐渐靠近并最终穿越-180°平面，且穿越该平面时对应的频率以形如幂函数（其指数小于0）的形式逐渐减小，系统变得愈发不稳定.综合上述两点可以看出，随着输入时滞的增加，闭环系统抑制外部干扰的能力减弱，即系统稳定性下降.

3 实验研究

3.1 实验设备介绍

本实验基于磁悬浮轴承-转子实验台进行，其中主要包含控制器、上位机、变频器、功率放大器、传感器板、电源开关、磁悬浮轴承-转子系统、示波器.AMB-转子系统实验平台如图16 所示.基于数字信号处理和控制工程（digital Signal Processing and Control Engineering，dSPACE）进行控制算法的实现以及信号在线分析，其采样频率设置为20 kHz，利用PID控制器使转子稳定悬浮.为了模拟压缩机等磁悬浮旋转机械在远程运行时产生的传输延时，在该实验台的控制回路中人为增加一延时环节作为外部输入时滞.后文所提时滞均指人为增加的外部输入时滞.

图16 AMB-转子系统实验平台Fig.16 AMB-rotor system test platform

3.2 Hopf分岔存在性实验研究

图17 为τ=0.75 ms 时Hopf 分岔前系统相轨迹图.从图17 中可以看出，系统相轨迹最终将收敛至一点，此时系统是稳定的，即1.2节提到的“定点稳定性”，与仿真趋势（图4）保持一致.

图17 τ=0.75 ms时Hopf分岔前系统相轨迹图Fig.17 System trajectory before Hopf bifurcation at τ=0.75 ms

图18和图19分别为τ=0.76 ms时Hopf分岔系统相轨迹图和频谱图.从图18 中可以看出，此时系统发生了Hopf分岔，最终获得了稳定的周期解，结合理论和仿真分析可知，此时系统出现了极限环，与仿真趋势［图5（a）～图5（d）］保持一致.从图19 中可以看出，当系统发生Hopf分岔时，其频谱主要包含极限环运行频率对应谱线，即101 Hz的主频谱线，以及主频的倍频谱线，此处主要为主频的2倍频谱线和3倍频谱线，与仿真［图5（e）］基本保持一致.

图18 τ=0.76 ms时Hopf分岔系统相轨迹图Fig.18 System phase trajectory diagram when Hopf bifurcation at τ=0.76 ms

图19 τ=0.76 ms时Hopf分岔系统频谱图Fig.19 System spectrum diagram when Hopf bifurcation at τ=0.76 ms

图20 展示了τ=0.77 ms 时极限环破裂后系统相轨迹.结合图18 和图20 可以看出，随着输入时滞的进一步增加，极限环破裂，相轨迹发散失稳，与仿真趋势（图6）保持一致.需要指出的是，理论求得的τ0≈ 0.637 ms、τ临≈0.682 ms 与实际系统的0.75 ms≤τ0＜0.76 ms、0.76 ms＜τ临≤0.77 ms 虽然在量级上相同、数值上相近，但仍存在一定的误差，分析原因主要有：①由于在理论及仿真中为简化系统建模，忽略了电磁力的非线性等因素，导致所建模型与实际系统存在一定误差；②在求解系统临界时滞τ临时，采用了近似替换，即计算求得的τ临为近似值；③实验过程中包含环境因素在内的实验误差干扰.

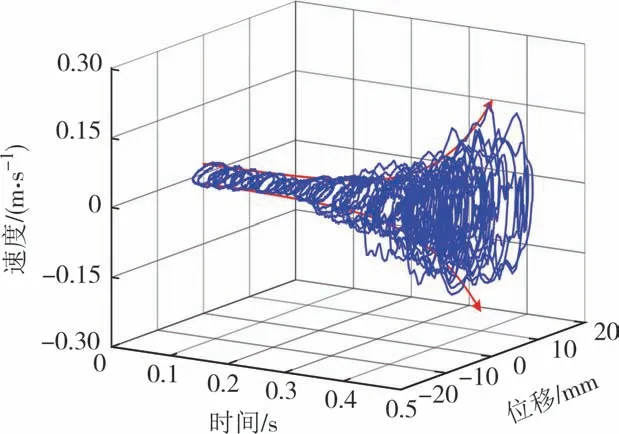
图20 τ=0.77 ms时极限环破裂后系统相轨迹Fig.20 System phase trajectory after limit cycle rupture at τ=0.77 ms

3.3 控制参数对时滞系统稳定性的影响

3.3.1 比例增益对时滞系统稳定性的影响

在磁悬浮轴承-转子实验台中，PID 控制器的kI=1、kD=0.001 5.为了验证理论及仿真分析的正确性以及更直观的说明kP变化对系统稳定性的影响，对τ=0.76 ms，kP分别取2.0、2.2 及2.4 时系统相轨迹的变化情况进行了分析，如图21所示.

图21 τ=0.76 ms时不同kP下系统的相轨迹对比Fig.21 Phase trajectory comparison of the systems under different kPat τ=0.76 ms

从图21中可以看出，随着kP的增加，系统的相轨迹由内向外逐渐从定点稳定变为稳定周期运动，最后变为发散失稳，与仿真趋势（图8）保持一致.与仿真不同的是，由于实验台中存在保护轴承，系统的相轨迹不会无限发散，而是被保护轴承限制在一相对空间内，此时转子与保护轴承已发生碰撞.

3.3.2 微分增益对时滞系统稳定性的影响

在主动磁悬浮轴承-转子实验台中，PID 控制器的kP=2.2，kI=1.为了验证理论及仿真分析的正确性以及更直观地说明kD变化对系统稳定性的影响，对τ=0.76 ms，kD分别取0.001 0、0.001 5 及0.002 0 时系统相轨迹的变化情况进行了分析，如图22所示.

图22 τ=0.76 ms时不同kD下系统的相轨迹对比Fig.22 Phase trajectory comparison of the systems under different kDat τ=0.76 ms

从图22 中可以看出，随着kD的增加，系统的相轨迹由外向内逐渐从发散失稳变为稳定周期运动，最后变为定点稳定，更加形象地说明了kD的增加将弱化输入时滞对于系统稳定性的影响，有利于提高系统的稳定性，与仿真趋势（图11）保持一致.

4 结论

本文以PID 控制的单自由度主动磁悬浮轴承-转子系统为研究对象，研究了输入时滞对系统稳定性的影响.在理论层面，推导了系统失稳临界时滞的近似值，对系统内Hopf 分岔的发生条件及存在性进行了分析；在仿真方面，分析了控制参数kP、kD对时滞系统稳定性的影响，验证了Hopf分岔的存在性，并通过探究输入时滞对闭环系统幅频和相频特性影响的角度来反映输入时滞对系统稳定性的影响；最后针对仿真内容进行了相应的实验研究.结果表明：

1）kP较大时，其与系统稳定裕度呈反比关系，kP的增加将放大输入时滞对系统稳定性的影响，对系统的稳定性起阻碍作用；系统的稳定域随kD的增加呈线性增加趋势，适当增加kD将弱化输入时滞对系统稳定性的影响.因此，在解决实际工程应用面临的时滞问题时，应当通过适当减小kP值或增大kD值的方式来提高系统的稳定性.

2）当系统输入时滞小于τ0时，未发生Hopf 分岔，系统表现为“定点稳定性”；而当输入时滞大于τ0且小于τ临时，系统发生Hopf 分岔，最终获得稳定的周期解，并产生极限环，此时系统的频谱主要为极限环运行频率（主频）对应谱线以及主频的倍频谱线；随着输入时滞的进一步增加，极限环破裂，系统最终发散失稳.

3）随着输入时滞的增加，闭环系统幅频响应曲线的峰化现象加剧，系统谐振频率的峰值显著增大；相频响应曲线逐渐靠近并最终穿越-180°平面，且穿越该平面时对应的频率以形如幂函数（其指数小于0）的形式逐渐减小.这表明在输入时滞影响下，系统对外部干扰的反应强烈，抑制外部干扰的能力减弱，系统的稳定性下降.