基于改进动力学方程的轮式装载机行驶失稳阈值分析

曹源文,周世华,梅宇航,谢利丹,宋书彬

(1. 重庆交通大学 机电与车辆工程学院,重庆 400074; 2. 浙江美通筑路机械股份有限公司,浙江 海宁 314400;3. 河南郑州路桥建设投资集团有限公司,河南 郑州 450006)

0 引 言

车辆失稳现象是指车辆在行驶中因外部作用影响而发生的侧滑、失控、倾翻等行为,这是一种十分严重的安全事故。轮式装载机的工作环境相对恶劣,工作时外界冲击较大,整车质心会发生较大偏移,这就导致轮式装载机相对于其他类型车辆而言更容易发生失稳现象[1-2]。R.CLARKE等[3]通过对美国工程机械事故统计分析发现:倾翻事故在工程机械事故中的占比高达56.7%,其中有10%左右的事故造成了车毁人亡。目前,针对车辆稳定性研究主要集中于公路车辆稳定性和安全控制两个方面。

在公路车辆稳定性研究方面:S.RAKHEJA等[4]提出:可将侧向加速度阈值作为判断车辆是否失稳的一个因子,并进行预警;D.HYUN等[5]定义了横向载荷转移率(LTR),并用于描述车辆出现侧翻的可能性,通过建立重型半挂工程车的动态模型,提出了一种预测车辆LTR与发生倾翻危险之间联系的新方法。在非公路车辆稳定性研究方面:A.REHNBERG等[6-7]设计了一种较为适用的轮式装载机械悬架系统,并分析了该系统在行驶时的横向稳定性与铰接点处阻尼大小及扭转刚度之间的关系,指出非公路车辆的轮胎(尤其是大尺寸轮胎),其动态性能对车身横向稳定性影响是不确定的,并讨论了动态性能对车辆横向稳定性影响的重要程度;张玉新[8]从轮式装载机的操纵和结构参数入手,深入研究了其对装载机倾翻稳定性的影响;李刚炎等[9]对车辆质心与侧倾稳定性变化之间的关系进行了仿真,分析了前者对后者的影响规律。由此可见:虽然针对非公路车辆稳定性的研究在逐渐增多,但针对非公路车辆领域特别是铰接式车辆运动中的失稳阈值分析尚不多见。

传统轮式装载机模型不能实时反映工作中的运行状态和轮胎受力。笔者为了能准确描述轮式装载机(以下简称“装载机”)前、后车体动态行驶轨迹和轮胎实时受力情况,对传统轮式装载机模型进行了改进,建立起了能反映改进后的装载机行驶中实时动力学模型和方程。基于装载机在不同路况下,前、后车体实时受力情况及横向载荷转移率,对装载机失稳影响因素阈值进行了分析。

1 改进后的动力学方程建立

1.1 系统自由度解析

装载机由前、后两个车体及后桥组成。这3个部分各有6个自由度,如图1。由图1可知:前、后车体之间由铰接相连,限制这两者的是除绕z轴转向外的其他5个自由度;同理,后车体与后桥的铰接亦如此。若将铰接转向角作为输入值,则此时系统自由度变为7个。

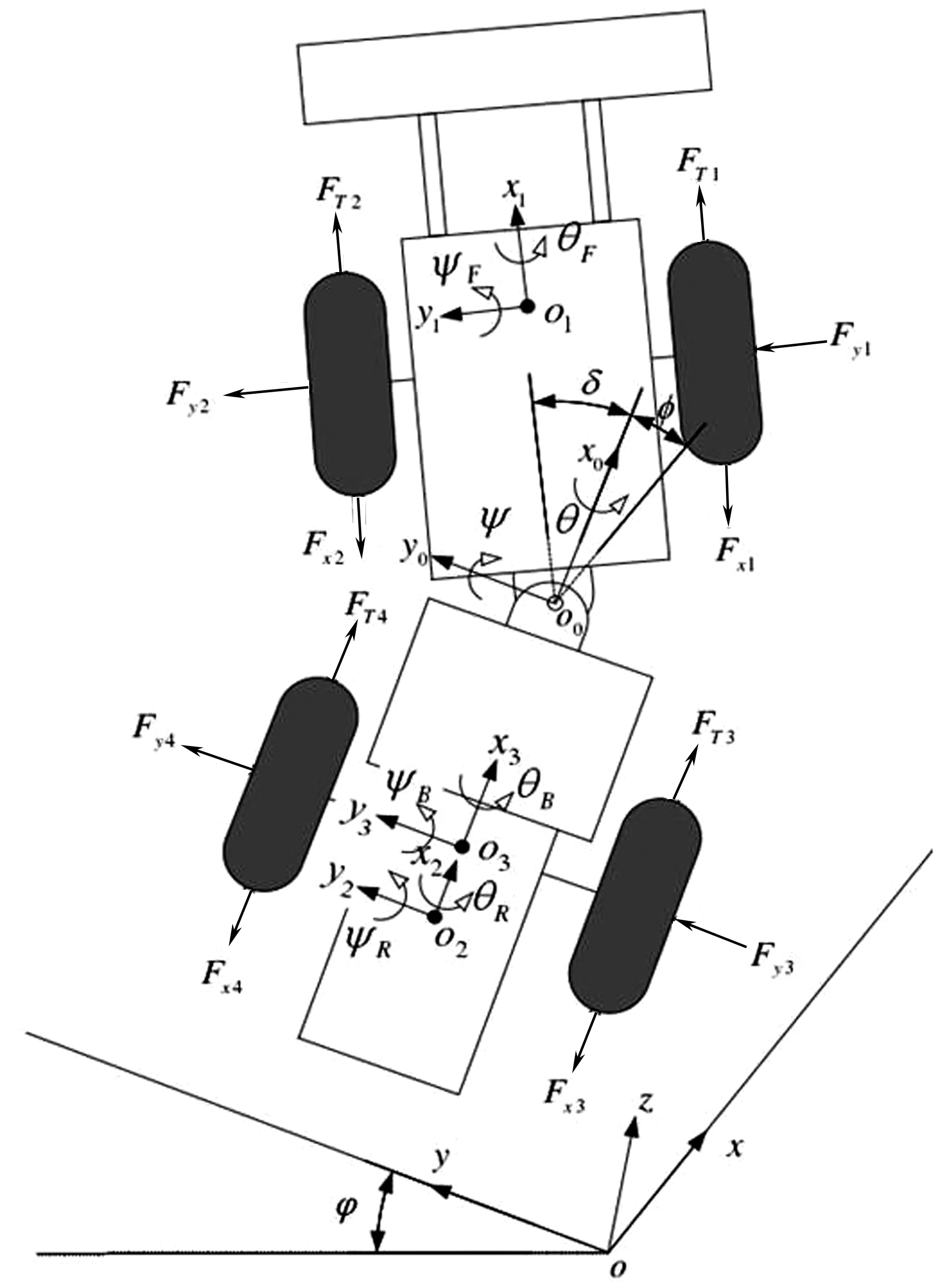
图1 轮式装载机自由度解析Fig. 1 Analytical diagram of the degree of freedom of the wheel loader

图1中:o_xyz、o1_x1y1z1、o2_x2y2z2、o3_x3y3z3分别对应地面、前车体、后车体和后桥的参考坐标系。利用坐标系o0_x0y0z0对前、后车体的铰接点进行描述,显然o0_x0y0z0相对于o_xyz具有6个自由度。对于装载机而言,这6个自由度可认为是其相对与地面3个方向的位移:x为纵向位移,y为横向位移,z为垂向位移;3个方向的转动:绕x的侧倾角θ,绕y的俯仰角ψ,绕z的横摆角φ,此时剩余一个独立自由度为后桥绕摆动桥的侧倾运动θ1。

1.2 实时行驶动力学方程

基于上述自由度解析,笔者建立了装载机传统行驶动力学模型。该模型表达了装载机行驶中的侧倾角度、位移等自由度变化情况,但局限之处在于无法描述出行驶中前、后车轮的运行轨迹。装载机失稳研究不仅需要考虑其在行驶中的稳定性,还要考虑车身受力变化情况及前、后车体运行轨迹,因此笔者建立了能反映装载机在行驶中的实时动力学模型,如图2。

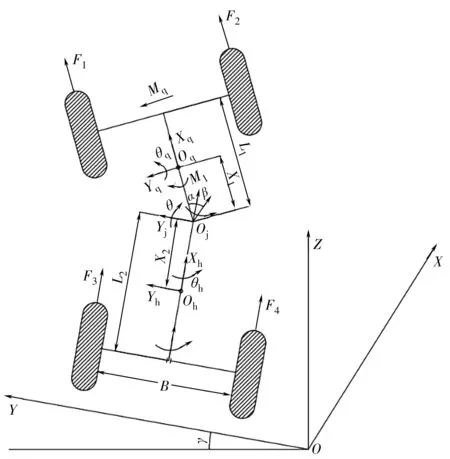
图2 轮式装载机行驶动力学模型Fig. 2 Driving dynamics model of wheel loader

假定装载机时始终保持匀速,Oj为装载机前车体和后车体铰接点,β为转向时装载机铰接点Oj处折腰角。装载机转向时由转向力矩M1和前轮横向力矩Mq共同作用进行控制,Mq的作用是使前轮在转向时在侧向上不会产生滑移,M1的作用是使装载机转向角能达到输入的转向角。将折腰角β、转向角α及后车体质心位移这3个变量作为对象进行研究。

依据上述分析并结合牛顿欧拉方程,建立装载机转向实时行驶动力学方程:

(1)

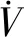
行驶过程中最大位移约束:

(2)

前后车身质心处的加速度关系:

(3)

根据虚位移法,可得前车俯仰角:

(4)

(5)

后车俯仰角:

(6)

Δyq=Δθq(L2-X2)

(7)

(8)

求解装载机右后轮反力F4的计算如式(9):

(9)

式中:Δy4为右后轮虚位移;θ为质心Oj处俯仰角;Δyq为前车体虚位移;Δyh为后车体虚位移;H2为后车体质心高度。

同理,左后轮反力F3的计算如式(10):

F3Δy3=m1gcosθΔyq+m1gcosθΔyh-m2(a2+

gsinθcosγ)H2Δy3/B

(10)

左前轮反力F1的计算如式(11):

F1Δy1=m1gcosθΔyq+m1gcosθΔyh+m1(a1+

gsinθcos(γ+θ))H2Δy4/B

(11)

右前轮反力F2的计算如式(12):

F2Δy2=m1gcosθΔyq+m1gcosθΔyh-m1(a1+

gsinθcos(γ+θ))H2Δy4/B

(12)

相对于传统模型,笔者所建立的模型能表达出在转向过程中装载机车体载荷受力情况及前后车轮的运动轨迹。由于微分方程的复杂性,笔者将行驶转向角、斜面坡度角和装载机质量特性参数等作为输入变量,利用MATLAB中的ode15i作为解算指令,对运动微分方程进行求解。

1.3 轮胎实时受力分析

轮胎与地面的接触合力按照产生作用可分解为:法向力Fz、横向力Fy、纵向力Fx和回正力矩Tz。在常用的轮胎模型中,Fiala轮胎模型不仅综合考虑了轮胎的横向力、侧向力、侧偏角、回正力矩及外倾角这4者之间的关系影响,同时还考虑了轮胎因受力而产生的复杂变形。故笔者将Fiala轮胎模型作为装载机的轮胎模型进行受力分析。

1.3.1 轮胎法向力

轮胎法向力Fz的计算如式(13):

(13)

式中:Kz为轮胎垂直刚度;MT为轮胎质量;Cz为轮胎垂直阻尼系数;δT为轮胎变形量。

1.3.2 轮胎纵向力

轮胎纵向力Fx与Fiala轮胎模型纵向滑移率的临界值有关。

Fx=-Ks×Ss

(14)

(15)

Fiala轮胎纵向滑移率的临界值:

(16)

式中:μs为静摩擦系数;μd为动摩擦系数;vx为前进速度;vy为横向速度;Ks为纵滑刚度。

1.3.3 轮胎横向力

轮胎横向力与轮胎的法向力、轮胎侧偏角及摩擦系数有关。

(17)

式中:Kα为轮胎侧偏刚度。

当轮胎为弹性变形时,|α|<αc,则有:

(18)

当轮胎为滑动时,|α|>αc,则有:

Fy=μ×|Fz|× sign(α)

(19)

1.3.4 轮胎回正力矩

当轮胎为弹性变形时,|α|<αc,则有:

Tz=(2×μ×|Fz|×r2)×(1-H)×

H3× sign(α)

(20)

当轮胎为滑动时,|α|>αc,则有:

Tz=0

(21)

2 稳定性评价指标和影响因素

2.1 评价指标选取

横向载荷转移率(LTR)是一项用于反映装载机发生倾翻危险可能性的评价指标,且只与车辆在行驶过程中所受到的垂直载荷有关,因此可将行驶过程中由其他干扰因素排除,获得准确的车辆行驶稳定状态。笔者选取RLTR作为装载机行驶时是否稳定的评价指标,如式(22):

(22)

式中:Fli为第i根车轴左侧轮胎上的垂直载荷;Fri为第i根车轴右侧轮胎上的垂直载荷;n为车轴总数。

由式(22)可知:RLTR介于0～1,当RLTR=0时,车辆各轴左右轮胎法向力大小分布都非常对称,车辆行驶较为平稳;当RLTR=1时,此时车辆某一侧车轮法向反力为0,即车轮将要离开地面或已经离开地面,车辆已处于侧翻危险状态。为了安全考虑,笔者将RLTR的安全阈值定为0.9,即在装载机行驶中:若RLTR<0.9,装载机正常稳定行驶;若RLTR>0.9,装载机发生倾翻。

2.2 影响因素分析

装载机行驶中的速度、斜坡坡度角、转向速度、行驶转向角等主要参数变化将会导致行驶稳定性发生改变,这些参数都存在一个阈值范围,当装载机工作参数不在此范围內时就会发生失稳现象。

此外,由于装载机工作时通常是在平直、斜坡、弯道及斜坡弯道等复杂路况之间连续不断的来回行驶。不同路况对装载机行驶稳定性造成的影响也有所区别:当在斜坡上行驶时,坡度角会对车辆稳定性具有一定影响;在弯道上行驶时,由于存在曲率半径带来的弯道角影响,加之行驶过程中车辆需要进行转弯操作,因此容易引起转弯失稳;而斜坡弯道兼具上述两者影响,在坡度角及弯道角共同影响下,对车辆行驶稳定性要求进一步提高。

3 装载机行驶失稳阈值分析

装载机主要质量特性参数如表1。

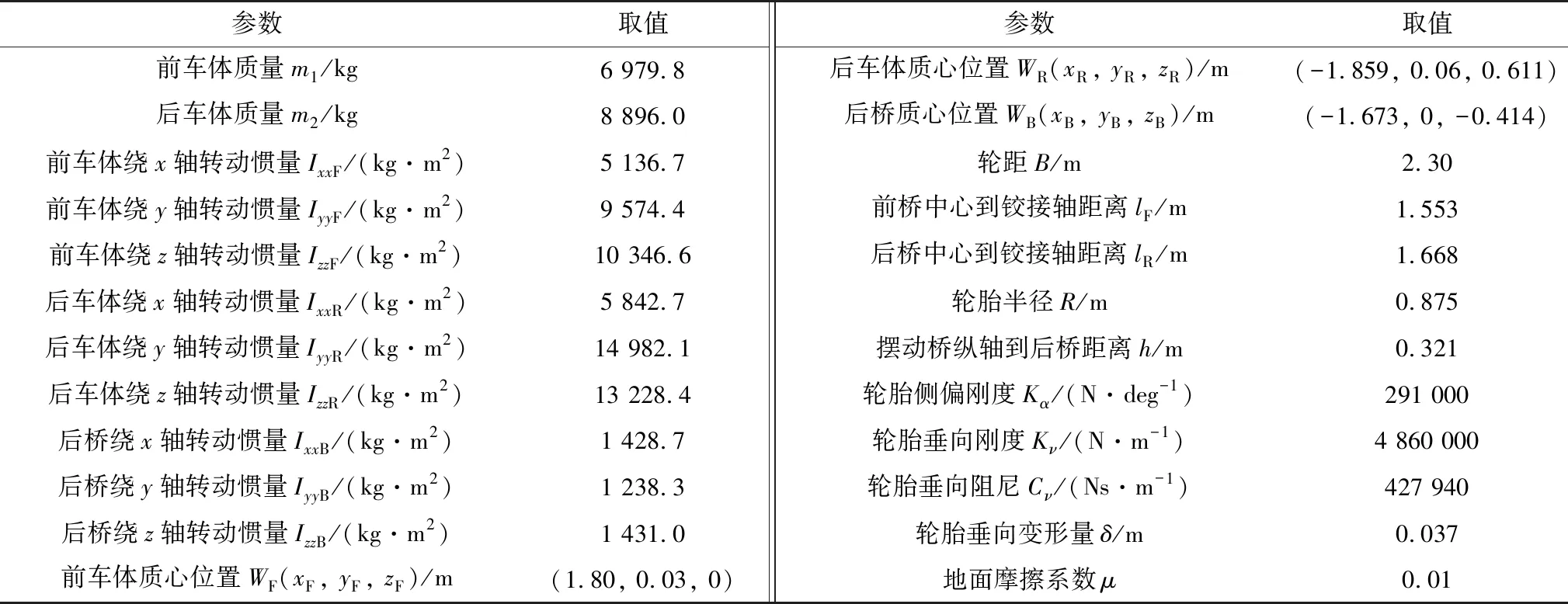
表1 装载机主要质量特性参数Table 1 The main quality characteristic parameters of wheel loader

3.1 速度对稳定性影响及失稳阈值分析

将装载机设置为在满载状态下行驶,速度取v=5～30 km/h。分析其在水平、斜坡、弯道及斜坡弯道上行驶时RLTR随时间变化的趋势,如图3。由图3可知:装载机速度小于20 km/h时,各路况下的RLTR均小于0.9,处于安全阈值范围内;当速度为20 km/h时发现:斜坡弯道下的RLTR=1.38,这说明此时装载机已发生失稳,如图3(d);当速度增大至25 km/h时发现:斜坡下的RLTR>1,存在失稳侧倾风险,如图3(b);当速度增大到30 km/h时发现:在平直路况下转向和弯道上的RLTR无限趋于1,会发生失稳现象,如图3(a)、图3(c)。

为了得到装载机行驶速度在不同路况下的最大失稳阈值,将图3各路况下的不同速度RLTR最大值进行连接,如图4,其中水平红线为安全阈值RLTR=0.9。图4中:各线段与水平红线交点即为所对应路况下的速度最大阈值。即:装载机在平直、弯道路况下的速度最大阈值均为28 km/h;在斜坡路况下的速度最大阈值为22 km/h;在斜坡弯道下的速度最大阈值为15 km/h。

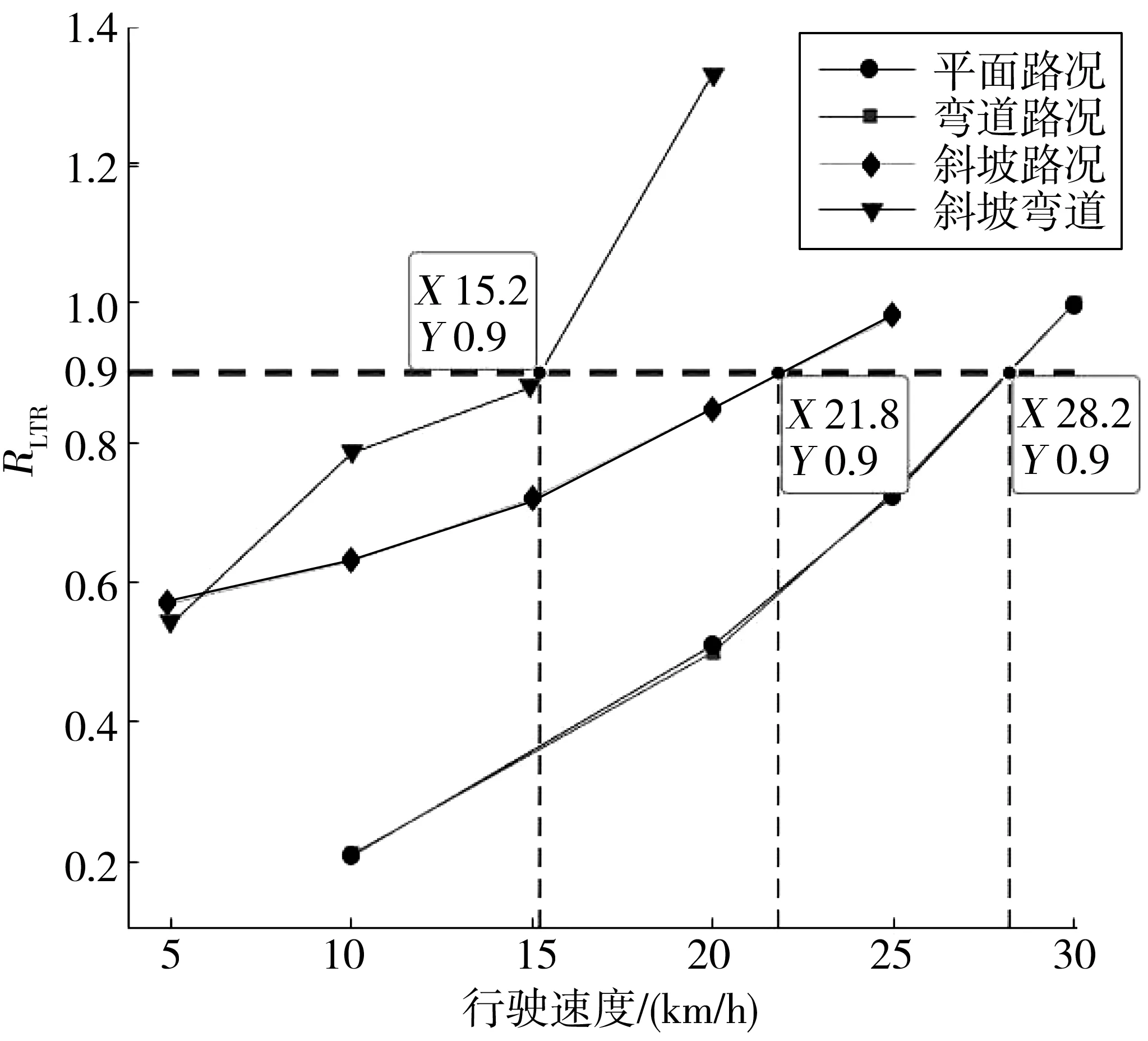
图4 最大RLTR随行驶速度变化对比Fig. 4 Comparison of the maximum RLTR changing with driving speed

3.2 斜坡坡度角对稳定性影响及失稳阈值分析

将装载机设置为在满载状态下行驶,设定以v=20 km/h匀速行驶,斜面坡度角为γ=5°～30°。由于已存在坡度角,故研究其在斜坡和斜坡弯道路况下的RLTR随时间变化趋势,如图5。由图5可知:当坡度角小于15°时,装载机的RLTR最大值均小于0.9,处于安全阈值范围内;当坡度角增大至20°时,在斜坡弯道下的RLTR最大值超过了0.9达到1以上,存在失稳侧倾危险,如图5(b);当坡度角增大至25°时,在斜坡路况下的RLTR也超过了阈值0.9,发生失稳现象,如图5(a)。

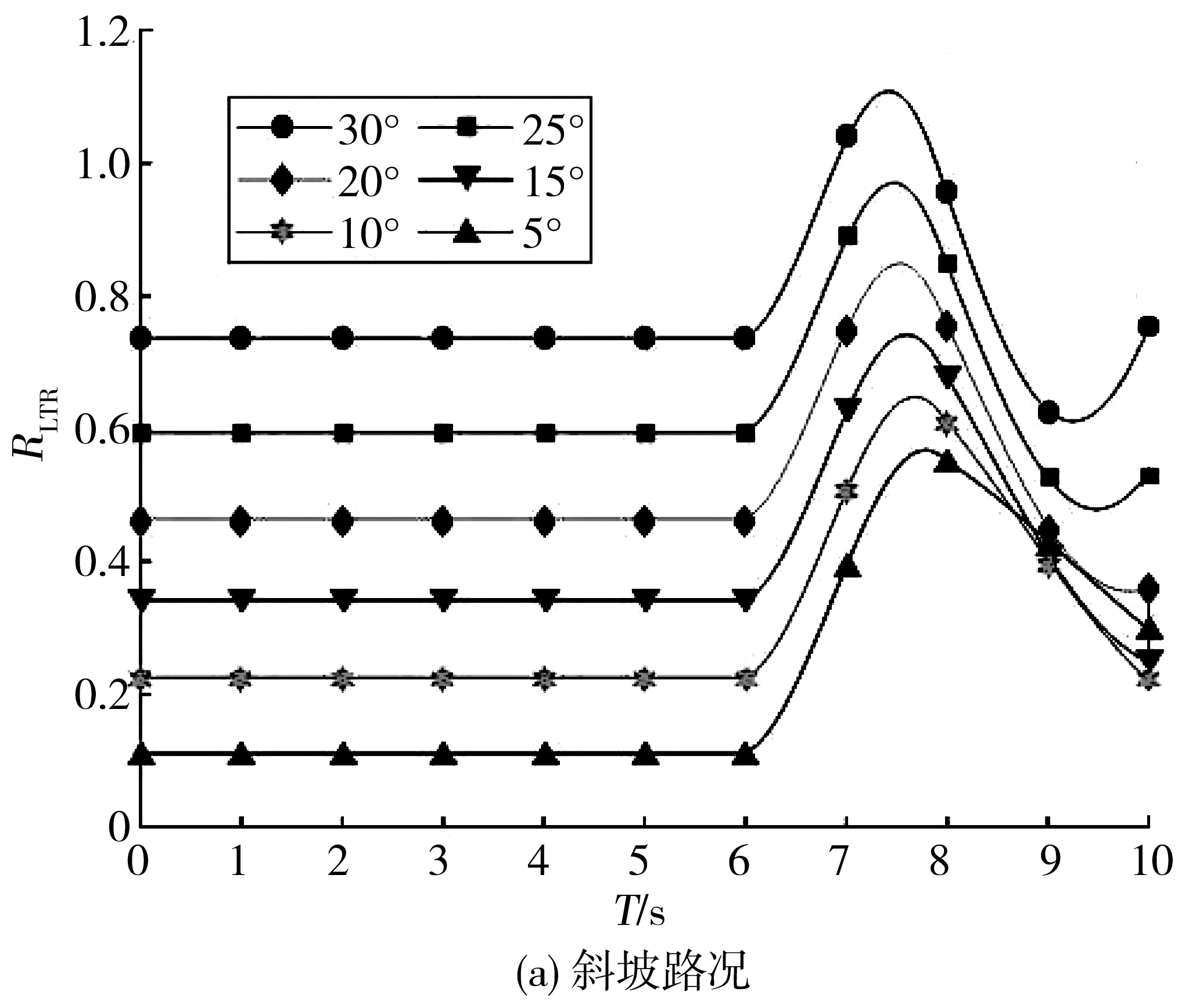
图5 不同路况、不同角度时RLTR随时间变化曲线Fig. 5 Variation curve of RLTR changing with time under different road conditions and angles

同理,将图5中各路况下的RLTR最大值进行连接,如图6。图6中:装载机在斜坡和斜坡弯道路况下行驶时,随着坡度角逐渐增大,装载机RLTR最大值也随之逐渐增大,当坡度角大于15°后,RLTR最大值超过了其在斜坡路况下的RLTR最大值,极其容易发生失稳。图6中各线与水平红线交点即为对应路况下的坡度角最大阈值,即装载机在斜坡路况下的坡度角最大阈值为22°;在斜坡弯道路况下的坡度角最大阈值为17.5°。

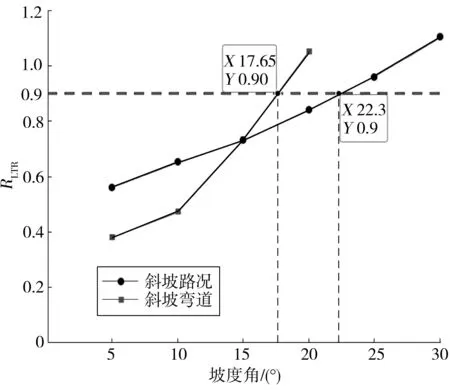
图6 最大RLTR随路面角度变化对比Fig. 6 Comparison of the maximum RLTR changing with road angle

3.3 转向速度对稳定性影响及失稳阈值分析

将装载机设置为在满载状态下行驶,速度取v=20 km/h,转向速度为装载机在6～7 s、6～8 s、6～9 s、6～10 s内完成20°转向,在平直和斜坡路况转向过程中,采用不同转向速度的RLTR随时间变化的趋势,如图7。由图7可知:装载机在平直路况下(时间间隔为1、2、3、4 s)完成转向的RLTR变化差异较小,最大值均为0.5,即都能保证安全稳定行驶;在斜坡路况下(时间间隔为1、2、3、4s)完成转向的RLTR最大值随转向时间间隔增大(即转向速度减少)而减小,其中在间隔为1s内完成转向时,其RLTR最大值大于阈值0.9,装载机已经发生了失稳现象。

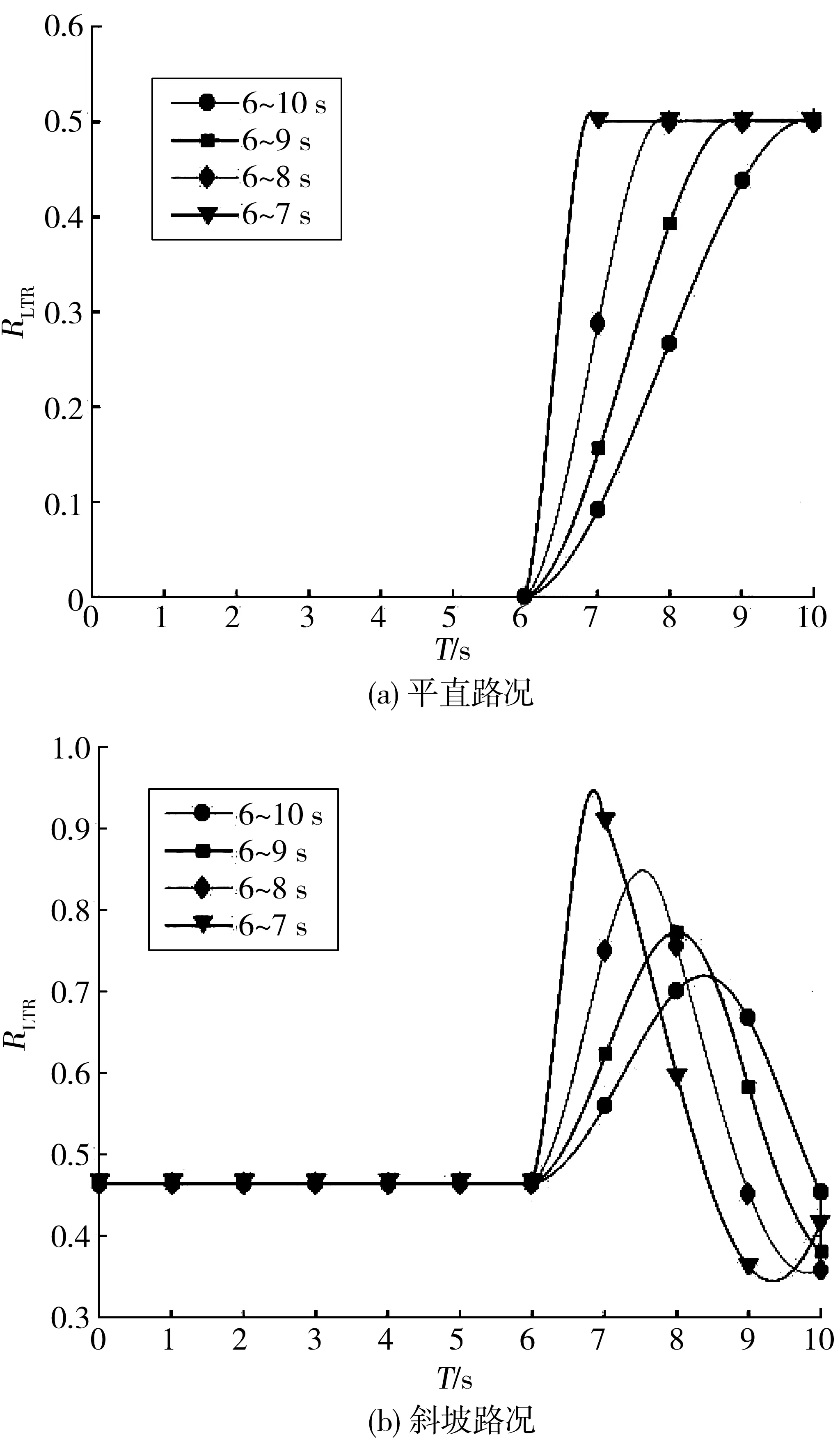
图7 不同速度转向时RLTR随时间变化曲线Fig. 7 Variation curve of RLTR changing with time when turning at different steering speeds

将图7各路况下的不同转向速度RLTR最大值进行连接,如图8。图8中:各线与水平红线交点即为对应路况下转向所需的最小时间间隔阈值,即最大转向速度。故装载机在斜坡路况下的转向时间间隔最小阈值为1.45 s。

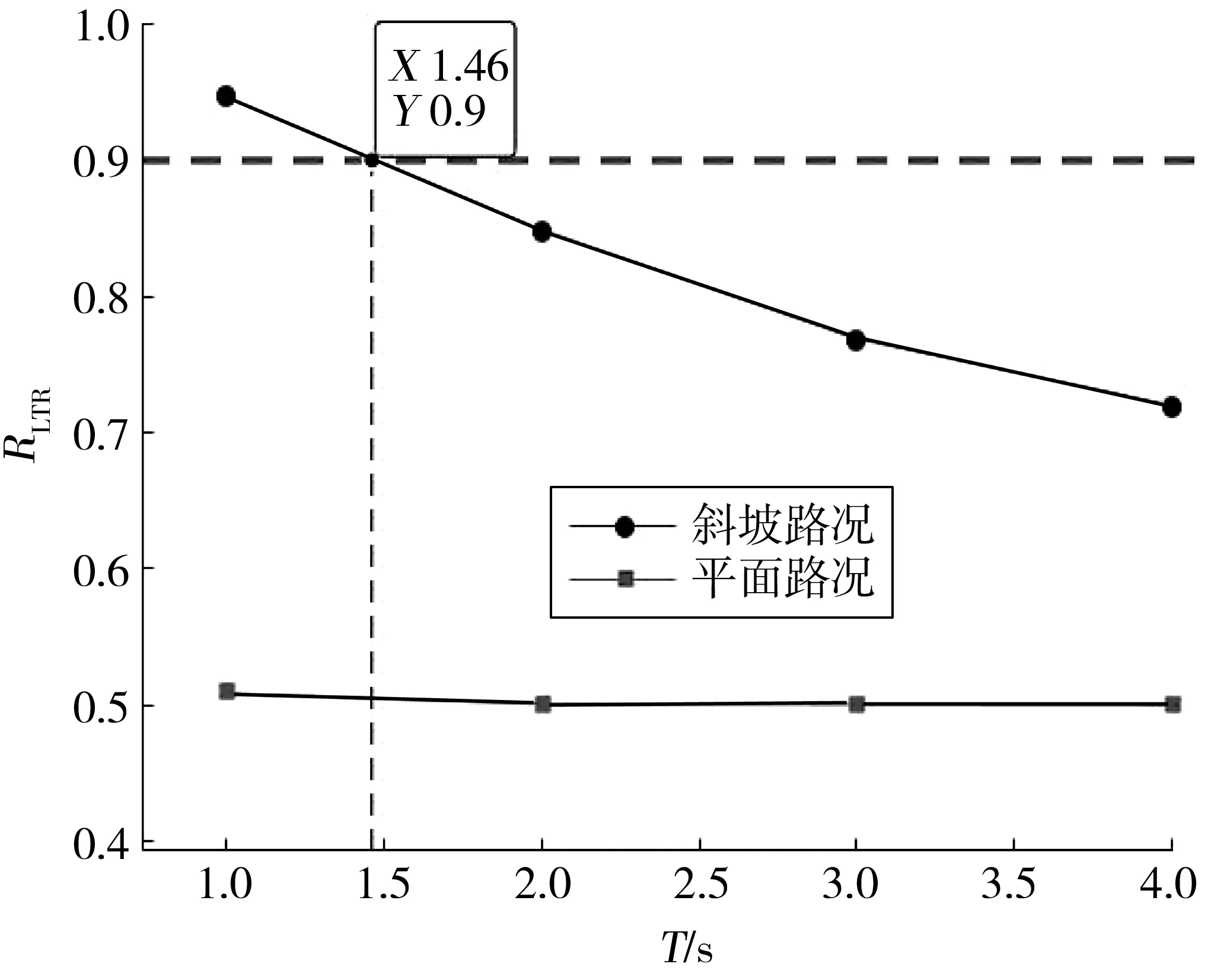
图8 最大RLTR随转向速度变化对比Fig. 8 Comparison of the maximum RLTR changing with steering speed

3.4 行驶转向角对稳定性影响及失稳阈值分析

将装载机设置为在满载高速状态下行驶,行驶转向角变化范围为15°～40°。研究装载机在水平、斜坡、弯道和斜坡弯道路况下的RLTR随时间变化趋势,如图9。由图9可知:当装载机转向角小于20°时,各路况下的RLTR都小于0.9,处于安全阈值范围内;当转向角达到25°时,在斜坡弯道路况下的RLTR最大值超过0.9,说明装载机此时已发生了失稳,如图9(d);当转向角增大至30°时,在斜坡路况下的RLTR最大值超过了阈值0.9,也存在失稳侧倾危险,如图9(c);当转向角增大至40°时,在平直和弯道路况下的RLTR最大值无限趋近于1,发生失稳现象,如图9(a)、图9(b)。

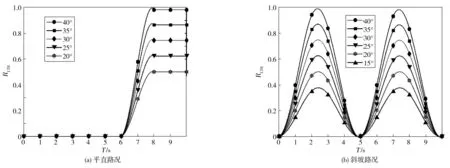
图9 不同转向角转向时RLTR随时间的变化曲线Fig. 9 Variation curve of RLTR changing with time when steering at different driving angles

将图9各路况下的不同转向角RLTR最大值进行连接,如图10。图10中:各线与水平红线交点即为对应路况下的速度最大阈值。即:装载机在平直和弯道路况下的行驶转向角最大阈值均为37°;在斜坡路况下的行驶转向角最大阈值为24°;在斜坡弯道路况下的行驶转向角最大阈值为23°。

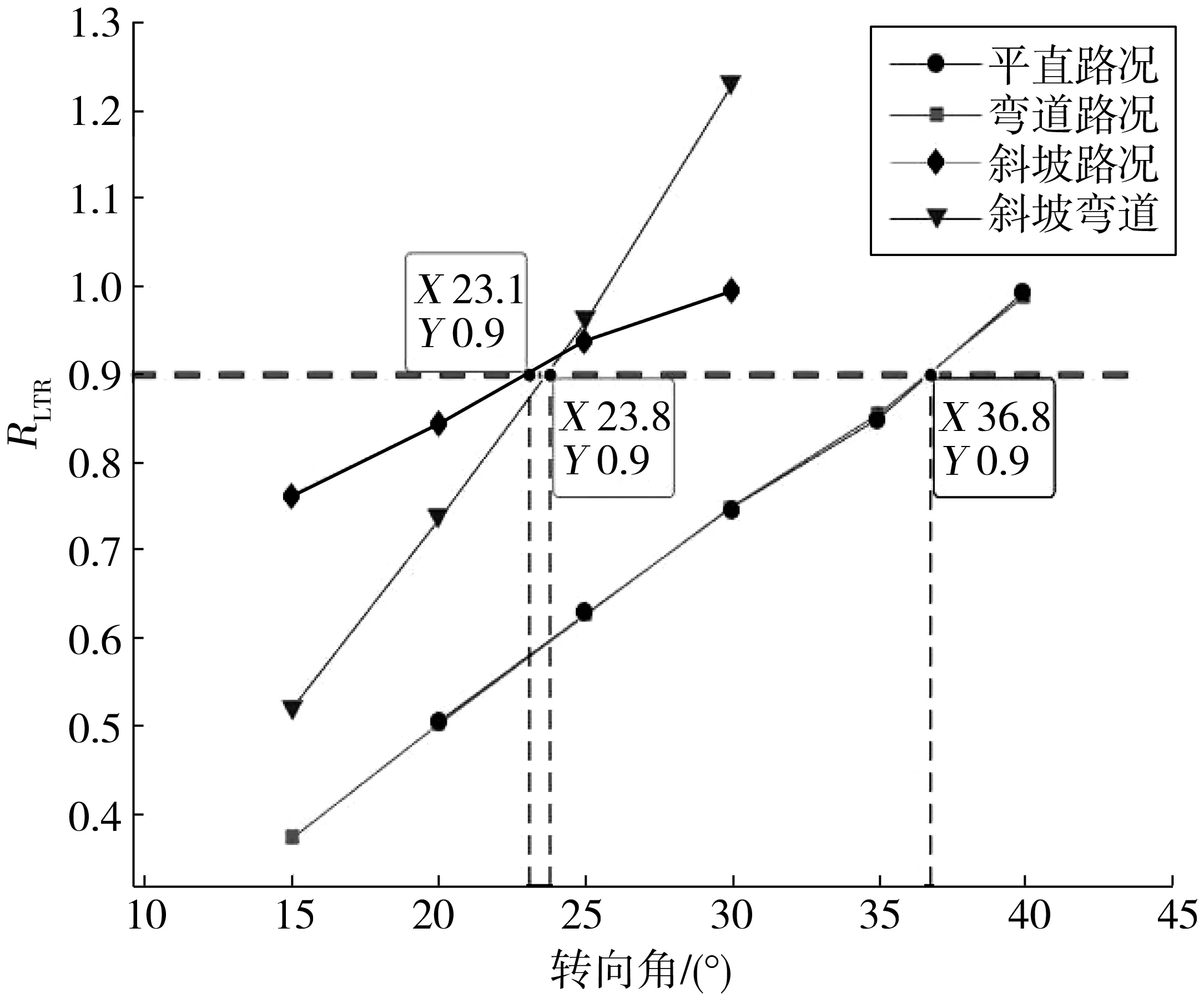
图10 最大RLTR随行驶转向角变化对比Fig. 10 Comparison of the maximum RLTR changing with driving steering angle

3.5 试验结果对比分析

由于实车试验的危险性以及成本太过高昂,不具备可行性,又由于通过比例模型样机试验能够得到与实车试验相近的验证效果,所以笔者利用吉林大学国家重点实验室轮式装载机等比例缩小模型样机对装载机在平直路况下转向以及斜坡路况下转向两种工况的情景进行对比验证,其工况如下:

① 平直路况下转向:分别以速度v=0.7、1.0 m/s在水平路面行驶一段时间,当速度稳定后的2 s左右进行转向操作。② 斜坡路况下转向:分别在坡度角γ=7.8°、10.4°的斜坡路面行驶一段时间,当速度稳定后的2 s左右进行转向操作。试验结果如图11。

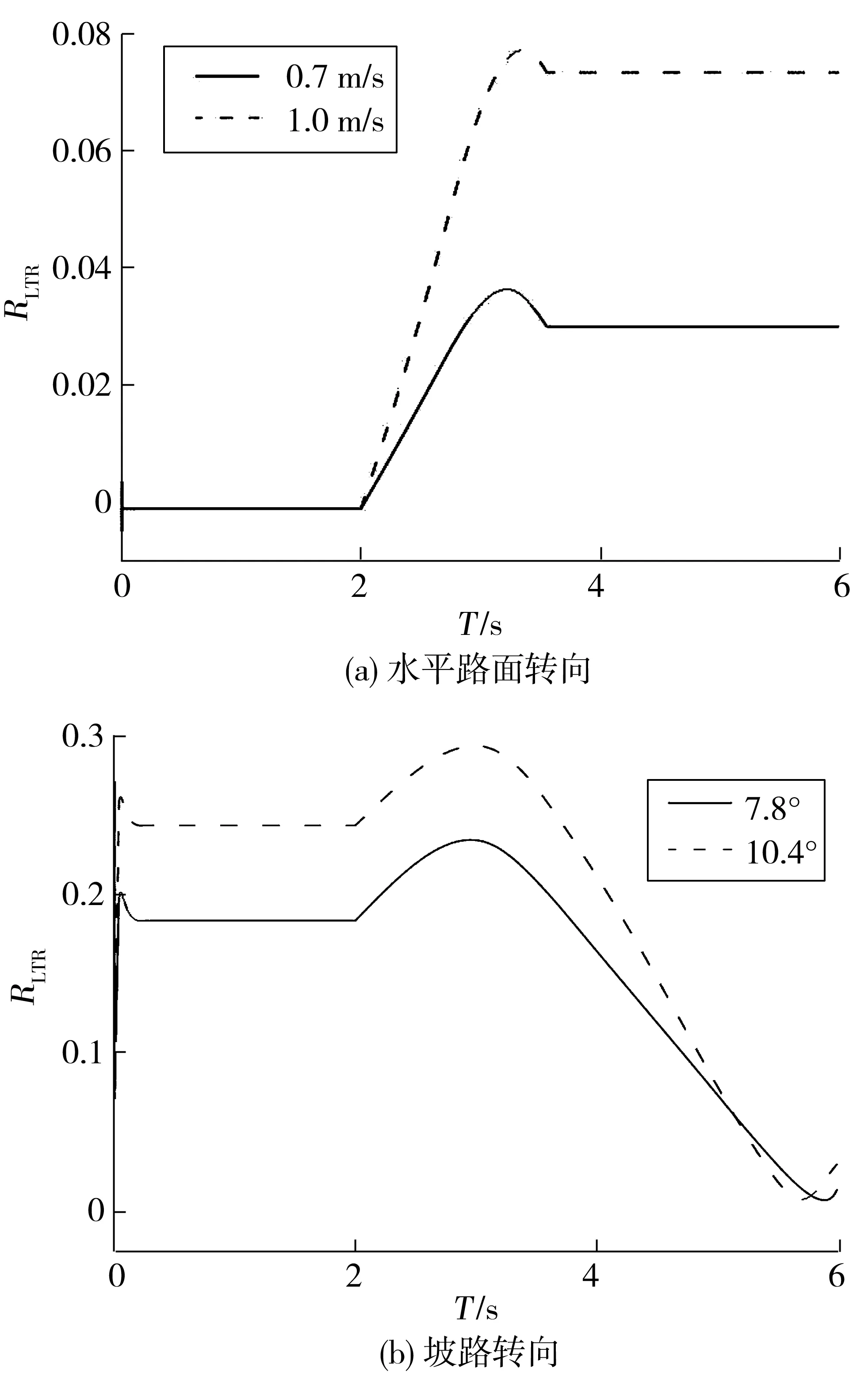
图11 水平和斜坡路况下转向的RLTR变化Fig. 11 Variation curve of RLTR when steering under horizontal road conditions and slope road conditions

图11(a)为在水平路况下,当速度分别为0.7、1 m/s时进行转向操作时装载机RLTR随时间变化情况。与图3(a)对比发现:试验和理论的RLTR变化趋势几乎一致,区别在于转向操作开始的时间不同。

图11(b)为在斜坡路况下,坡度角不同进行转向操作时装载机RLTR随时间变化情况。与图5(a)对比发现:试验和理论的RLTR变化趋势几乎一致。

4 结 论

1)基于传统动力模型进行改进,并对装载机行驶动力学模型的运动微分方程进行了计算求解。模型能反映装载机前后铰接两车实时运动轨迹和轮胎实时受力情况。

2)根据装载机行驶失稳的主要影响因素,分别以行驶速度、斜面坡度角、转向速度、行驶转向角作为变量,得到了多路况下RLTR随时间变化的规律曲线,并进行了失稳阈值对比分析。结果表明:① 针对不同路况,装载机失稳阈值建议值为:平直路况下,行驶速度阈值为0～28 km/h,斜坡路况下不超过22 km/h,斜坡弯道路况下不超过15 km/h;坡度角阈值为0～22°,斜坡弯道路况下不超过17.5°;转向速度阈值应大于1.45 s;行驶转向角阈值为0～37°,斜坡路况下不超过24°,斜坡弯道路况下不超过23°;② 装载机行驶速度和转向速度的增加、斜面坡度角和行驶转向角的增大,会严重加剧装载机倾翻失稳的风险;③ 基于最大RLTR变化曲线,RLTR随行驶速度和行驶转向角曲线变化率时最快,这一结论说明行驶速度和行驶转向角相对于其他参数而言对行驶稳定性的影响最为严重。