多端元模式下高光谱图像解混的不确定性问题

赵一凡,王立国,2

(1.大连民族大学 信息与通信工程学院,辽宁 大连 116605;2.哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)

高光谱技术是一种基于传统遥感技术的新型非接触式目标探测技术,如今的高光谱成像设备的光谱采样范围可以从可见光区域一直延伸至近红外和中红外区域,可将连续的光谱分离为若干独立的窄波段。由于其良好的光谱特性,高光谱遥感技术已被广泛应用于军事、农业领域、生态环境和地质勘探等领域[1]。

随着高光谱探测仪成像技术的发展,光谱图像的分辨率越来越高,但是由于现实环境的复杂性和物理条件的限制,每一个最小成像单位即像元中不可避免会出现包含两类及以上地物类别信息的情况,这样的像元一般称为混合像元[2]。为分析混合像元,高光谱图像解混技术应运而生,其致力于分析高光谱图像中存在的混合像元各类别所占比例的问题。目前研究较为广泛的解混算法有最小二乘法解混算法、非负矩阵分解算法(NMF)、原型分析法等[3-4]。由于最小二乘法物理意义明确,在已知光谱端元的情况下解混效率和精度均较高,故得到广泛使用[5]。

在一般的解混过程中,一个端元用于代表一个类别的地物,即单端元解混,但由于真实的物理环境中高光谱数据的采集和接收会产生一些无法避免的干扰,以及成像地物本身存在类内光谱变化等特点,这种方式的不准确性导致解混误差过大[6]。多端元解混技术在一定程度上克服了单端元解混的不足之处。Roberts等提出的多端元光谱混合分析(MESMA)算法,通过寻找大量的多端元组合模型为每一个像元找出使其解混结果最佳的多端元解混模型[7]。MESMA-SAD算法通过结合光谱角距离(SAD)与平均绝对误差(MAE)的值来减少端元组合的数量以提升算法效率[8]。基于端元束的光谱解混算法将距离很小的多个端元看作一个可以代表该类别的端元整体,来解决光谱类内差异问题[9]。

综上所述,多端元解混技术的发展虽然能在一定程度上提高解混的精度,但它带来的问题即不确定性却鲜有研究。从本质上讲,传统的精度评价是立足于整体的统计评价,而不确定性评价是立足个体,即关心个体像元的分析可靠性,二者既有联系又有区别,偏废任何一方都是不可取的。二者相结合可以实现个体评价与整体评价的辩证统一,形成完整、全面的评价体系,对获得“科学”的科学评价意义很大。为此,本文立足经典的线性光谱混合分析模型,研究不确定性的本质内涵,计算方法,及其降减方法,以获得多端元光谱解混方法的完整评价和性能提升。

1 多端元解混的不确定性问题

从本质上说,不确定性是由类内光谱变化造成的[10],具体特性与解混模型具有密切关系。在解混中产生的不确定性一般可分为两种,即混合像元位置不确定性和混合丰度的不确定性。下面将在二类解混的场景中分析这两种不确定性的实际含义。

1.1 丰度固定时像元位置的不确定性

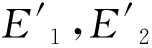
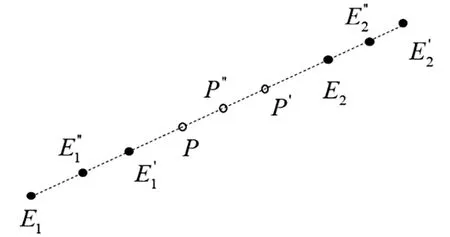
图1 线性排列的三组端元解混示意图

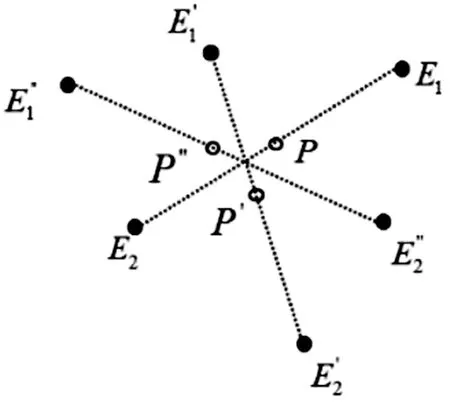
图2 随机排列的三组端元解混示意图

由上述两种情况进行推广,如图3。假设每一类可以作为端元的像元构成一个端元束,圆O1为第一类的端元束,O2为第二类的端元束。对于固定的混合比例α = (α1,α2)T,(α1,α2>0且α1,α2>0),可以找到一个与之对应的混合像元束,中最左侧的点是由端元组合成的,点是由合成的。混合像元束满足约束方程:

图3 混合像元位置的不确定

(1)

在这种情况下,混合像元的位置变化只受到类内端元变化的影响。

1.2 像元位置固定时丰度的不确定性

当已知一像元为混合像元,考虑其光谱可变性,如图4。不同的端元组、和将会得到不同的丰度比例,对于第一类的丰度可表示为

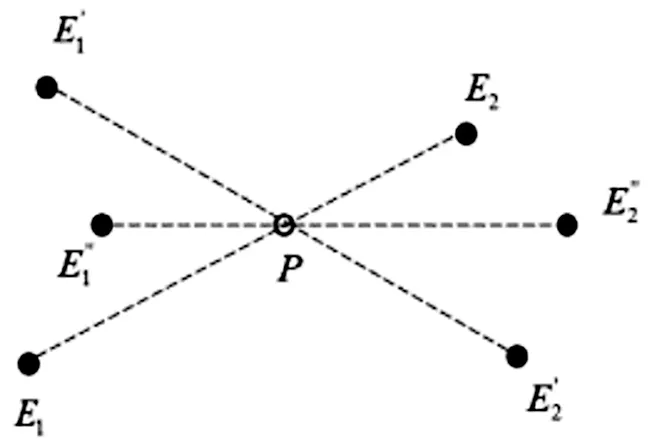
图4 解混丰度的不确定示意图

(2)

将上述的特殊解混模型进行推广,可以得到如图5所示的情形。根据几何解混方法,若不考虑类内光谱可变性的影响,此时解混端元为两个端元束的圆心(O1,O2),解混丰度不确定性为0,即λmax=λmin。在考虑光谱可变性的影响后,对应于第一类的最大分量丰度λmax和最小分量丰度λmin的计算公式为

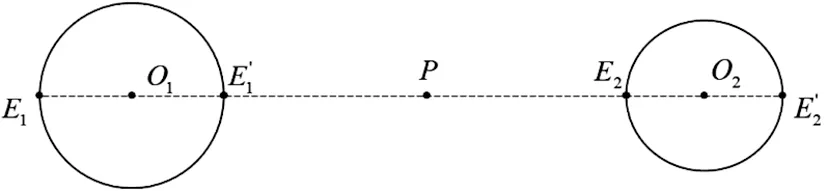
图5 解混丰度的不确定性

(3)

在实际应用中,这两种不确定一般更关心第二类即丰度的不确定,下面将立足流行的线性光谱混合分析(LAMA),给出丰度不确定性的定义及降减方法。

2 LAMA中丰度不确定性的定义及降减方法

2.1 LAMA多端元解混算法

假设待解混的混合像元矩阵X中的任意像元x均由A,B两类地物构成,单端元解混模式下,存在端元矩阵E,P为每类包含的端元个数,混合像元x可被表示为

x=Eα+n。

(4)

式中:α是由A类混合丰度值αA和B类混合丰度值αB构成的丰度矩阵;n为解混误差;使用最小二乘误差问题的建模方法,其模型表达式为

(r-Eα)T(r-Eα) 。

(5)

求解出的丰度值αA,αB均满足全约束最小二乘约束条件。

在多端元解混问题中,由于每类地物存在多个端元,两类地物的端元矩阵分别可表示为EA={eA1,eA2,…,eAP}、EB={eB1,eB2,…,eBP},解混使用的端元矩阵Eij=(eAi,eBj)T,i,j∈1,2,…,p为由EA中任意一个端元和EB中任意一个端元构成的端元矩阵。此时多端元解混最小二乘解混问题中混合像元的混合丰度矩阵,如式(6)。

(6)

2.2 丰度不确定性的定义

本文基于有监督的高光谱解混研究场景对高光谱解混不确定性进行研究,重点探究上文提到的两种不确定性问题之中的混合像元位置固定时的丰度不确定性问题。单个混合像元的解混不确定性α可定义为

(7)

其中:

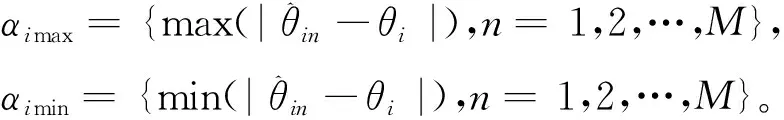
(8)

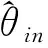
2.3 基于端元加权的不确定性降减方法

传统线性最小二乘高光谱解混方法(LS-LSMA)平均的考虑了端元组中每一个端元对混合像元的影响,对于真实高光谱数据,每一类地物端元组中的各个端元相互独立且包含不同的空间特征信息[11]。

同一类内每个端元对于混合像元解混应有不同的权重值,为了区分不同波段对混合像元构成的不同作用,为基于LSMM的LS-LSMA解混模型,提出基于端元加权的多端元解混方法(EW-LSMA),该方法引入一个加权矩阵A:

(r-Eα)TA(r-Eα) 。

(9)

找到合适的加权矩阵,表示各个特征波段的情况是本算法应用的关键,高光谱的分类技术中的常用方法Fisher判别法,通过类内散度矩阵来体现不同的特征对于分类效果的不同贡献,分类中使用的类内散度矩阵SW可以定义为

(10)

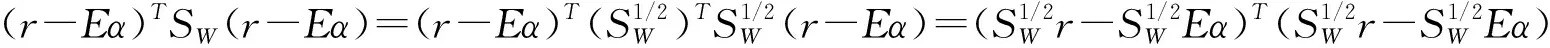
(11)

使用ξSW表示过加权矩阵SW线性变换处理后的矩阵:

(12)

使用类内散度矩阵对最小二乘法解混方法加权后的模型表达式为

(13)

样本加权的解混方法可以区分不同样本对于解混分析中不同的意义,通过训练样本对数据集进行学习,得出以对解混结果影响程度的大小进行度量的加权矩阵,对于产生解混异常程度较大的样本赋予更小的权重可以降低其对解混结果的不利影响,同时对产生更小异常的样本分配更大的权重增强对解混结果的正面影响。

以二分类的解混场景为例,任意混合像元x(x∈X)的丰度矩阵表达式为

(14)

式中,SA和SB为解混端元矩阵的加权矩阵,加权矩阵的加权形式通过端元样本的类内散度矩阵求出,表达式为

(15)

端元矩阵Eij求得的每一组解混结果表示为

(16)

3 实验结果分析

3.1 实验数据

本文实验采用真实高光谱数据与模拟数据相结合的方式,实验使用的高光谱数据集是Indian Pines和Salinas两组经典高光谱数据集。Indian Pines数据集波段数为200,图像中一共包含16类地物信息;Salinas数据集包含224个波段,共计16类地物信息。Indian Pines和Salinas数据集的图像展示如图6～7。其中6a、7a为相应高光谱图像的单波段显示,6b、7b为样本类别标签的分类灰度显示。表展示了后续实验中使用两组数据的部分类别地物的名称与数量信息,见表1与表2。本文选择样本数目较多的类别光谱进行实验分析,排除样本选取的偶然性对实验结果准确性造成的影响。

表1 Indian Pines 部分地物类别名称及数量统计表

表2 Salinas部分地物类别名称及数量统计表

a)单波段显示 b)类别信息图6 Indian Pines数据集

a)单波段显示 b)类别信息图7 Salinas数据集

3.2 解混不确定性计算及规律分析

随机在实验类别的地物光谱库中选取不重复的纯像元按随机混合比例构成合成混合像元,按照此方法共合成1 000个混合像元进行多端元解混不确定性验证。设ki为第i个像元距离类内标准端元的欧氏距离,像元矩阵Kn为第n类地物中全部像元,按照ki正序排序。端元选取范围N为选取Kn中前N个像元作为待选取端元。

在Indian Pines数据集中6类地物构成的合成像元矩阵在不同的端元选择范围N下丰度变化的平均值,见表3。解混结果不确定性随端元选取范围的增大逐步增加,实验证明解混中的不确定性存在且解混的不确定性大小与端元选取的结果密切相关。

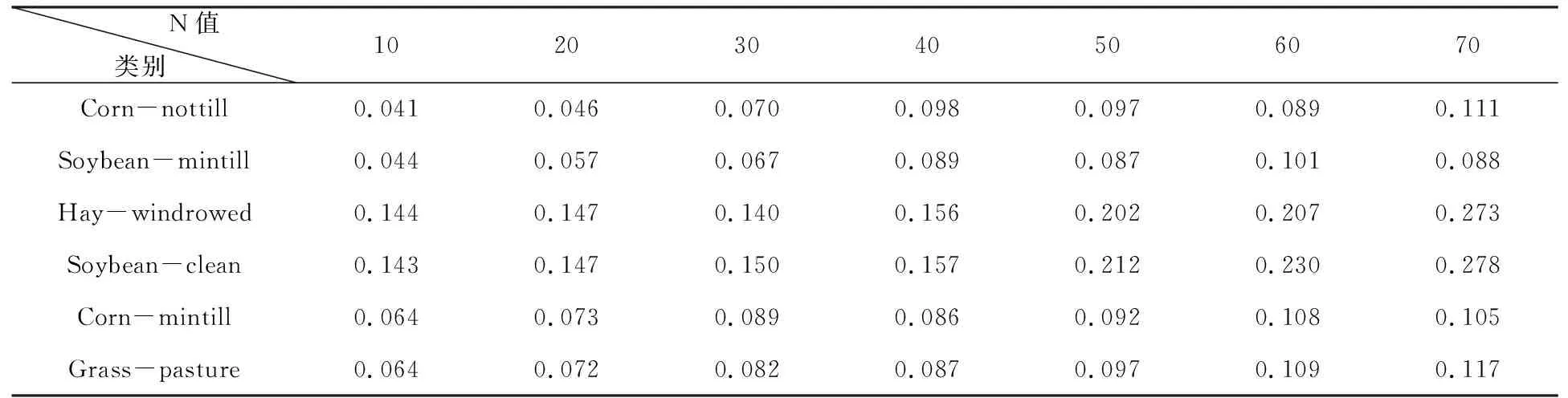
表3 不同N值下解混不确定性变化

3.3 不确定性降减算法性能验证

使用传统的LS-LSMA与本课题提出的EW-LSMA分别对两组数据集进行二类多端元解混实验,实验使用蒙特卡洛随机方法随机选取两类地物构成100个混合像元,每个数据集共进行5组实验,统计解混结果的误差与不确定性,见表3～7。

实验结果表明:两种解混方法均会产生解混误差,两组数据集的实验数据见表4～5。本文提出的EW-LSMA多端元解混方法在一定程度上可以降低解混误差,在两组数据集的测试中均略微改善了误差计算表现。表6～7对比展示了两种解混方法解混不确性的差异,数据表明使用基于端元加权的解混方法在二分类的多端元解混问题中可以有效降低解混的不确定性,在不增加算法的解混误差的情况下可以有效提高算法的结果稳定性。

表4 Indian Pines数据集解混误差对比

表5 Salinas数据集解混误差对比

表6 Indian Pines数据集解混不确定性对比

表7 Salinas数据集解混不确定性对比

4 结 论

本文主要探究了在高光谱数据的多端元解混过程中产生的不确定性问题,并通过实验进一步证明了不确定性的存在。结果表明解混不确定性的大小与多端元解混选取的端元组距离该类地物端元的欧氏空间离散程度有关。本文提出的基于端元加权的最小二乘多端元解混算法,通过衡量每个端元与混合像元的空间相关性大小,赋予多端元不同的权值。实验结果表明,加权多端元解混算法与传统算法相比能有效降低解混不确定性,进一步提升了解混算法的性能。

目前的实验仅在二分类的多端元解混领域对解混的不确定性进行探究与分析,并且由于解混不确定性的存在使得当前对于多端元解混算法的算法评价方法不够完善。在后续研究中,将继续研究多分类解混中的不确定性问题,继续验证新算法在新场景中的指标优化能力,关注利用混合像元与端元的空间关系信息。在降低不确定性的同时保证解混的精度,从而最大程度利用多端元解混方法相较单端元解混的优越性,同时研究完善现有的算法评价体系,将解混不确定性作为评价算法效率的一个重要指标,增加解混算法评价方法的应用价值与实际意义。

最后强调的是,多端元解混技术较之前序单端元解混技术存在不确定性问题,但这并不否认后者的优势。不确定性问题从发现到理解再到有效利用,进一步巩固和提升了多端元解混技术的性能。“不确定性”是内涵信息的,是揭示问题的,是有警示功能的,是可加利用的。“兼听则明”,生产生活亦或科学研究,莫不如此。