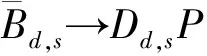QCD因子化框架下衰变过程的研究

常钦,赵萌非,陈丽丽,王晓琳

(河南师范大学 物理学院,河南 新乡 453007)

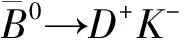
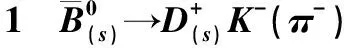
表分支比的理论值、实验测量值以及偏差

总的来说,除了上述两个衰变道以外的其他衰变道还是会有来自湮灭图的贡献.因此在QCDF框架下对它们的分支比进行可靠的计算,同时考虑非零的c夸克质量(mc)和D介子质量(mD)对顶角修正、旁观者和湮灭图的贡献[5].对端点发散问题的处理仍然采用文献[6]中B→PP两体非轻衰变给出的解决方案和输入参数.同时,结合光前夸克模型(LFQM)处理非微扰物理量.通过数据分析解释了弱湮灭振幅贡献有一个比较大的Wilson系数C1但总的弱湮灭振幅的贡献A1非常小的问题.计算了旁观者散射和弱湮灭效应对整体分支比的贡献在O(10-2)量级,和之前的理论预言相比有所改善.

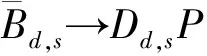
1.1 有效哈密顿量

(1)

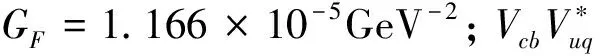
(2)

(3)

其中,α和β表示颜色指标,相同颜色指标表示求和.

1.2 强子矩阵元

在QCDF框架下[8]B介子两体非轻衰变B→M1M2的强子矩阵元可以表示为[9]

(4)

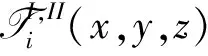
(5)

和

(6)

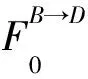
(7)

(8)

其中,B′≡ifBfDfP;V1,H1和A1分别是顶角修正,硬旁观者散射和湮灭图的贡献,可以分别通过计算图2、图3和图4得到.

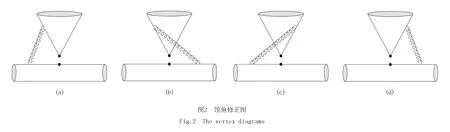
对于顶角修正贡献,通过计算图2可得:

(9)

其中,

(10)

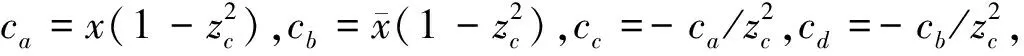
(11)

对旁观者散射图的贡献,通过计算图3,可得:

(12)

(13)

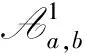
对于湮灭图的贡献,通过计算图4可以得到A1的完整表达式.研究表明,考虑D介子质量时,除了twist-2部分,P介子twist-3阶的光锥分布振幅对湮灭振幅有非零的贡献,这和B→PP衰变过程有明显不同[6,12-13].然而,相对于twist-2部分的贡献,这些贡献被因子rD和rμP压低,所以在接下来的计算中不再考虑这一贡献.采用上述近似,湮灭图的贡献可以表示为:

(14)

(15)

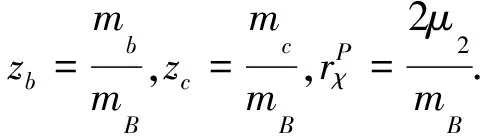
2 数值结果和讨论

2.1 输入参数

在讨论数值结果之前给出输入参数[14]:

(16)

夸克质量取值[14]:

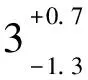
(17)

mc=(1.67±0.07)GeV,mb=(4.78±0.06)GeV,mt=(172.76±0.30)GeV,

(18)

其中,mq≡(mu+md)/2.对于确定的费米耦合常数、介子质量和B介子的寿命,采用PDG给出的参数[14].

本文利用光前夸克模型(LFQM)计算的衰变常数、形状因子和标度为μ=1 GeV下的盖根保尔矩,

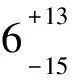
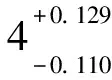
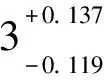
2.2 数值结果

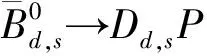
表2 |α1|的实验测量结果和理论预言值

理论上由于弱湮灭振幅贡献有一个比较大的Wilson系数C1,其对整体振幅的贡献可能比旁观者散射大很多.然而,数值上得到:

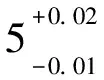
(19)

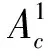
表3 CP平均分支比的理论预言值

3 总 结