平方图的2-距离和可区别边染色

王芹,杨超,姚兵

(1.上海工程技术大学 数理与统计学院;智能计算与应用统计研究中心,上海 201620;2.西北师范大学 数学与统计学院,兰州 730070)

1 预备知识

染色问题是图论中的经典问题之一,具有较强的应用背景,它解决了如存储问题、课程表问题、电路设计等众多实际问题[1].2002年,ZHANG等[1]首次提出了图的邻点可区别正常边染色,即在正常边染色的基础上区分相邻点的色集合,相关研究成果详见文献[2-8].对于两个不同的集合,它们的元素之和可能会相同,但若两个集合元素之和不同,则这两个集合一定不同.2013年,FLANDRIN等[9]提出了图的邻和可区别正常边染色,需要考虑相邻顶点边色集合的元素之和,即图G的一个正常边染色满足任意相邻两点的色集合的元素之和不同.2021年,强会英等[10]在邻和可区别边染色的基础上考虑将相邻点扩展为距离不超过2的点,提出了图的2-距离和可区别边染色的概念,并研究了无K4-子式图的2-距离和可区别边染色.本文探讨5类平方图的2-距离和可区别边色数问题.

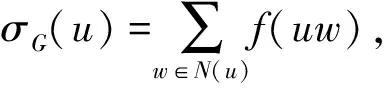
定义2设u和ν分别表示连通图G和H中的最小度点,称图G∧H表示将G中的点u与H中的点ν粘连一起后得到的图.

定义3[11]图G的平方图G2是以V(G)作为它的点集,任意两个点u,ν在G2中相邻当且仅当1≤distG(u,ν)≤2.

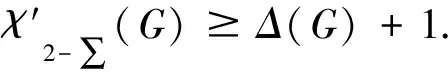
本文论及的图均为有限、无向、连通的简单图.设N(u)表示u的邻点集,Δ(G)(或Δ)表示图的最大度;设u,ν为图G中任意两点,称满足DG(u,ν)≤2的点为2-距离点.文中未定义的术语和符号均采用于文献[13].

2 主要结论

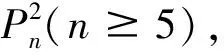
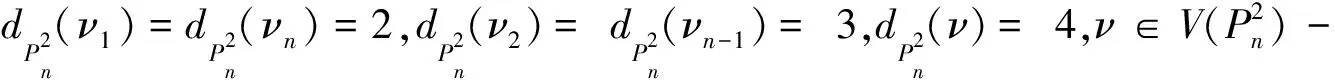
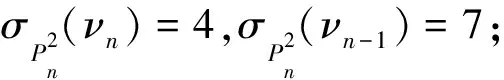
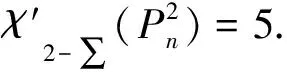
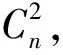
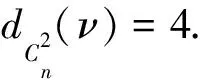
情形1n≡0(mod 5)

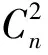
情形2n≠0(mod 5)

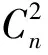
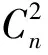
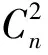
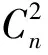
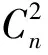
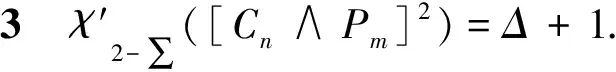
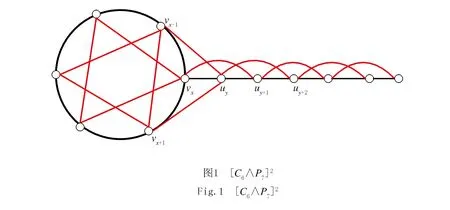
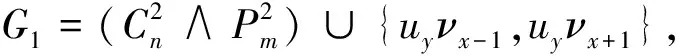
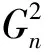
情形1n≡0(mod 5)

情形2n≢0(mod 5)

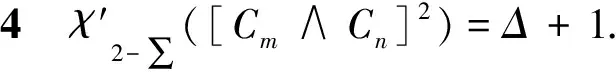
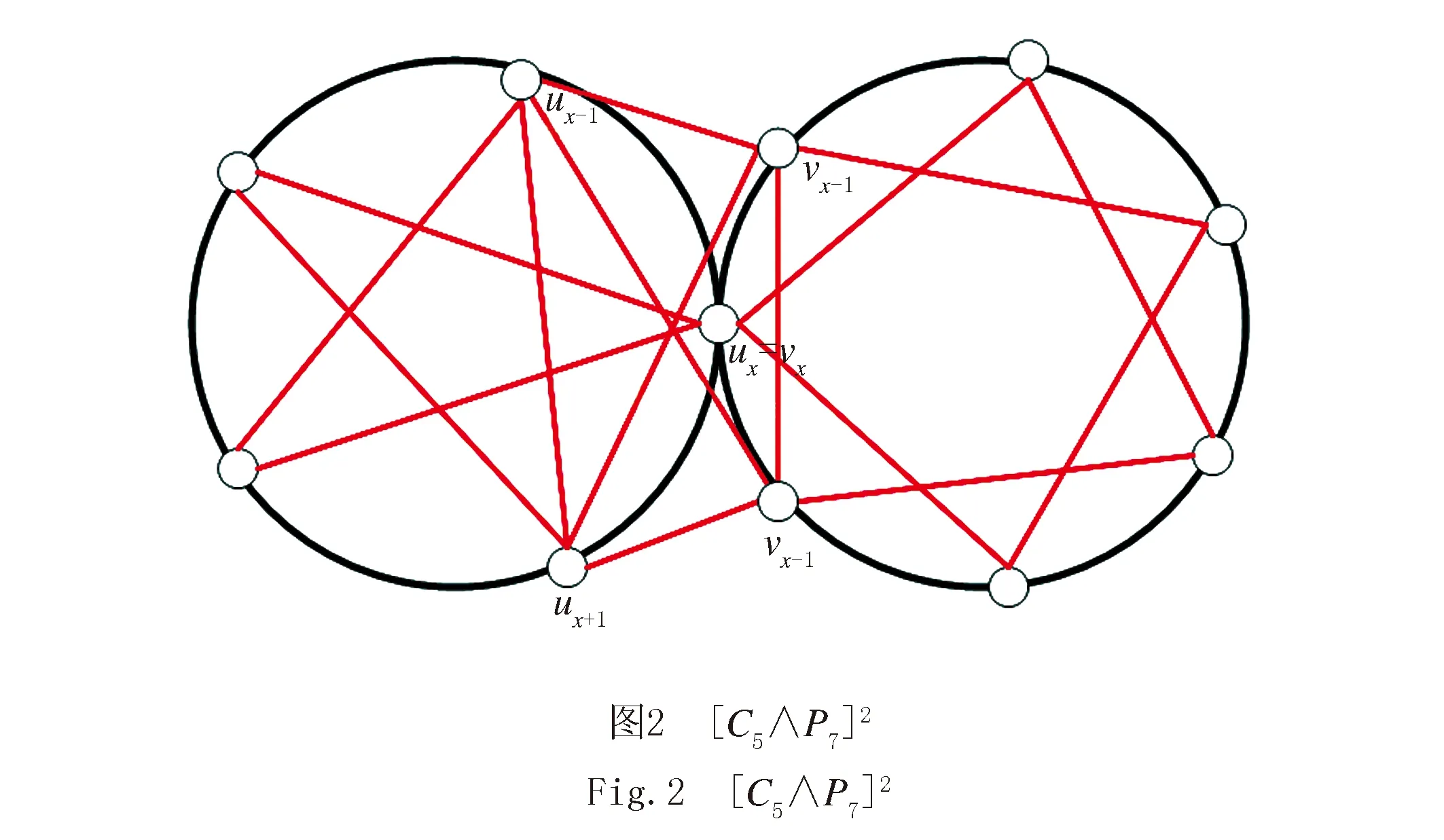
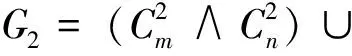
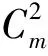
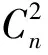
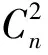
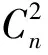
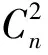
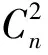
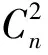
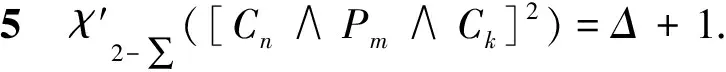
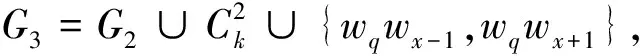
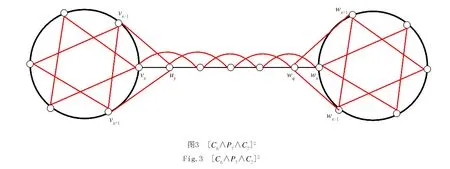
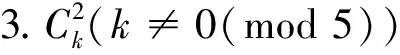
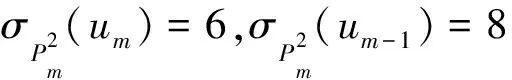
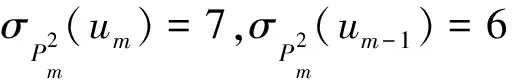
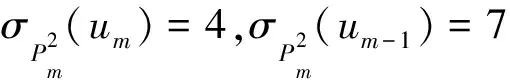
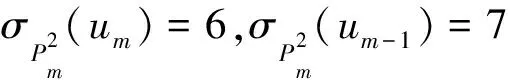
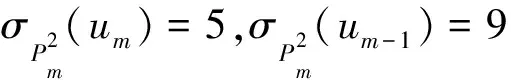
综上所述,结论成立.