基于巴特沃斯低通滤波的自适应步长梯度下降姿态解算方法

王柏森,卢艳军,2,张晓东,2,刘 冬

(1.沈阳航空航天大学自动化学院,辽宁 沈阳 110135;2.辽宁通用航空研究院,辽宁 沈阳 110136)

0 引言

近年来多旋翼无人机在复杂环境探索、低空城市搜救等场景广泛应用,飞行控制逐步由平缓小姿态向快响应大角度方向发展[1-2]。目前姿态测量系统受限于多旋翼无人机的体积与成本,多数仍依赖于陀螺仪、加速度计、磁强计构成的微型惯性测量单元(miniature inertial measurement unit,MIMU)[3],单一传感器一般采用高频采样(1～2 kHz)、数字滤波处理、低频输出(100～200 Hz)方案,在滤波预处理阶段,由于滤波器具有相位迟延效应致使原始数据输出存在一定时滞,导致无人机大角度姿态变换速率无法进一步提高[4]。针对以上问题,文献[5]提出基于巴特沃斯滤波的自适应卡尔曼姿态解算方法,有效剔除传感器原始数据噪声减缓姿态解算时滞,但该算法较依赖高性能处理器平台。文献[6]针对低成本处理器提出动态步长梯度下降姿态解算方法,有效抑制运动加速度对姿态解算的干扰,但在角速率变化快时将出现姿态解算滞后现象。

本文针对旋翼机使用低成本MIMU而造成的姿态原始数据预处理后具有滞后的问题进行研究,建立传感器误差模型后进行现场标定[7],根据零相位偏差原理修正巴特沃斯滤波时滞,设计自适应步长梯度下降姿态解算算法,并在低成本微处理器中验证了算法可行性和提高姿态信息获取的实时准确性。

1 MEMS传感器姿态解算原理

MEMS姿态解算中通常定义相对运动的导航坐标系(n系)和机体坐标系(b系)用以表达姿态变换关系,根据三轴坐标系正向不同指向可产生多个坐标系定义方式[8]。本文导航坐标系使用东北天系,机体坐标系使用右前上系进行姿态描述,初始时两坐标系的原点相互重合,并定义机体坐标系下绕X轴旋转的姿态角为倾仰角(θ),绕Y轴旋转的姿态角为横滚角(γ),绕Z轴旋转的姿态角为偏航角(ψ)。两个坐标系之间一般可用四元数法、欧拉角法、方向余弦法进行转换,其中欧拉角法因万向节死锁问题无法描述全姿态变化,方向余弦法涉及较多三角函数运算不适用低成本处理器中,因此本文使用四元数法更新姿态角变化,根据zyx顺规三轴姿态角有如下四元数表达方式[9]：

(1)

2 基于LPB的自适应梯度下降姿态解算

2.1 LPB参数初始化

传统低通滤波器处理姿态原始数据时,当载体作大角度变换时易受加速度高频噪声干扰,姿态测量与真实值存在一定时延,巴特沃斯低通滤波器(low-pass Butterworth filter,LPB)在处理线性相位与斜率衰减方面具有平坦过渡的特点[10],可有效剔除高频振动干扰,其增益平方幅度响应公式为

(2)

式(2)中,N为LPB滤波阶数,ω为输入角速度,ωc为LPB截止频率。由公式可得平方幅度响应是输入角速度的单调递减函数,滤波器阶数越高幅频特性效果越好,低频测量信号失真度越低。由阻带频率ωs确定阻带衰减As：

As=-20lg|H(jωs)|。

(3)

将幅频特性带入得

(4)

将上述数字角频率推导转换为模拟角频率后,通过查表确定传递函数G(s),再根据双线性变换将S域转换为Z域,通过求取G(z)系数确定LPB的参数,与传统滤波器特性相似的LPB也存在因相位偏移导致的时延问题。

2.2 数字滤波器相位时延的改善

根据零相位数字滤波器原理[11]进行预修正处理,将一定长度的姿态原始数据正向时间序列和反向时间序列通过LPB,根据正反时延差大小消除相位偏移,进而实现巴特沃斯滤波的零相位偏移。

假设x[n]是一组长度为N+1的单边序列,通过冲击响应为h[n]的LPB滤波后得到单边序列y1[n],对y1[n]进行时间序列反转处理并平移得到单边序列y2[n],再次通过冲击响应为h[n]的LPB滤波后得到单边序列y3[n],对y3[n]再次进行时间序列反转处理并平移得到y[n],即

(5)

将以上变换转为频域描述并整理后得到零相位滤波输入输出关系如下：

Y(ejω)=X(ejω)|H(ejw)|2。

(6)

从式(6)可知,输出Y(ejω)与输入X(ejω)之间理论不存在相位偏差,在实际应用时受限于低成本微处理器算力影响,当待滤波数据输入速率大于滤波器处理速度时仍将出现相位偏移现象,此时可通过在存储器中添加FIFO机制适当缓存待处理数据。该种方案将占用大量存储空间,因此需根据实际滤波效果适当选择滤波器阶数。

2.3 梯度下降算法姿态解算

梯度下降算法是一种求解函数极值的数学模型,其一般迭代公式为

(7)

式(7)中,∇J(a(k-1))为目标函数J(a(k-1))在某点a(k-1)的正梯度向量,μ为每次迭代的固定步长。

将n系中的重力矢量单位归一化处理,并将其三轴分解至b系得

(8)

将重力矢量在b系下的分量ab与加速度传感器测量值作差得到误差函数并将其用四元数法表达后可得

(9)

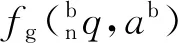
(10)

2.4 自适应步长梯度下降算法

上述梯度下降姿态解算中迭代步长μ为定值,在实际飞行中姿态变化平缓时解算跟随效果较好,当姿态变化迅速时定步长梯度下降迭代更新速率小于姿态变化速率,导致姿态更新迟滞。梯度下降迭代更新过程中迭代步长与机体运动时的角速度以及系统的采样时间成正相关关系[12]。

为避免弱动态飞行时频繁计算得到过小步长,消耗算力增加解算时延,引入机身运动状态估计因子α：

(11)

当状态估计因子α大于阈值α0时,开启自适应计算步长,否则使用定步长μ0解算姿态。

(12)

式(12)中,Ts为系统采样时间,ω为载体运动角速度。

综上,自适应梯度下降姿态解算迭代公式为

(13)

3 实验与结果

3.1 实验测试平台

以项目组自研飞控为平台,微处理器采用低成本ARM Cortex-M3芯片,MEMS传感器为ICM20602,定高传感器为气压计与超声波,水平定位传感器为光流,整机如图1所示。在无转台设备情况下,为验证本系统姿态解算效果使用高精度惯导系统输出的数据作为对比参考,如图2所示型号为440 Series Inertial Systems系列的AHRS440,该惯导可动态输出三轴姿态角度以及相关姿态原始数据,高精度惯导AHRS440参数如表1所示。将本系统与高精度惯性测量系统测量的数据在弱动态、强动态状态下作对比验证。

图1 多旋翼实验平台Fig.1 Multi rotor experimental platform

3.2 巴特沃斯滤波分析

首先通过快速傅里叶变换分析静止状态下传感器数据频谱图,提取噪声截止频率并初始化滤波器参数。图3为加速度原始信号(Raw)在低通滤波(LPF)以及不同阶巴特沃斯滤波(LPB-x)下响应曲线,由图中可知LPB滤波后数据更加平缓,但存在一定时滞。图4为LPF处理后加速度原始信号与未时延修正巴特沃斯滤波(LPB)和时延修正巴特沃斯滤波(ZLPB)后对比图,由图中可知零相位修正后时延得到显著改善,高频噪声部分得到剔除,同时当LPB阶数越高数据过度越平坦,时滞越大。图5为LPF与各阶ZLPB滤波对比,加入零相位修正后中高阶LPB仍存在较大时滞,因此采用二阶LPB。

图3 各阶LPB滤波效果Fig.3 LPB filtering effect of each order

图4 零相位修正对比Fig.4 Comparison of zero phase correction

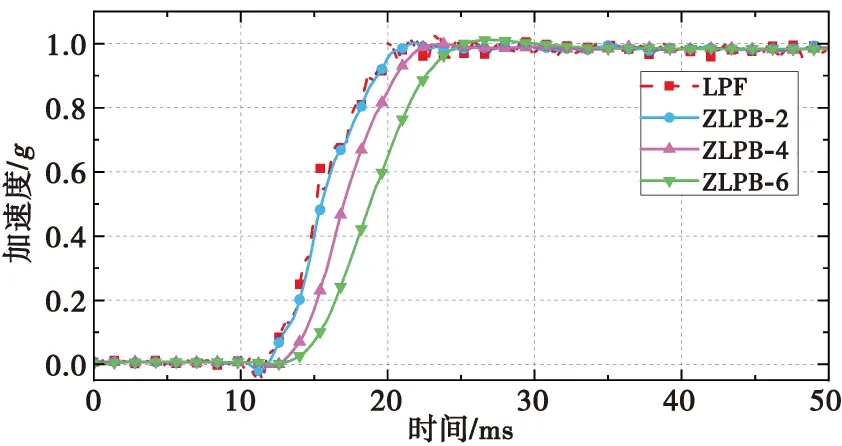
图5 各阶零相位修正LPB对比Fig.5 Comparison of zero phase correction LPB of each order

滤波器阶数选择与时延修正完成后开始处理姿态原始数据。为测量单次姿态解算时长,首先在无操作系统的处理器中设计足够长时间的定时器中断,并记录单次最长解算时间,测量发现在运行速度为72 MHz的处理器中单次采集MEMS姿态传感器9轴原始数据最高消耗1 ms,姿态解算最高消耗2.5 ms,为预留充足系统调度以及其他紧急任务时间,系统最小中断周期设计为5 ms,即传感器采样频率为200 Hz。

实际测试时磁强计作为航向修正观测量,无需高频滤波处理,只需测量加速度与角速度滤波效果。将MEMS姿态传感器低通滤波和时延修正巴特沃斯滤波后加速度数据与高精度惯导输出的加速度数据对比如图6所示。

图6 加速度数据处理对比Fig.6 Comparison of acceleration processing

由图6可知高精度惯导输出的加速度原始数据更加敏感,通过与LPF和AHRS440系统输出的数据对比可知,设计的ZLPB有效滤除了高频噪声使信号过度平坦,经过零相位修正后有效减小时延,误差对比如表2所示。

表2 时延修正滤波后优化结果Tab.2 Optimization results after time delay correction filtering

将MEMS姿态传感器低通滤波后角速度数据和时延修正后巴特沃斯滤波角速度数据与高精度惯导输出的角速度数据对比如图7所示,由图中可知ZLPB处理后的角速度数据时延更小、噪声低。

图7 角速度数据处理对比Fig.7 Comparison of angular velocity data processing

3.3 自适应步长梯度下降姿态解算分析

将两个相同器件飞控现场在线标定后,对比定步长梯度下降姿态解算(N-GD)与自适应步长梯度下降姿态解算(M-GD)分别在弱动态、强动态下姿态解析精度。图8为弱动态下姿态解析对比,由图中可知在弱动态条件下二者解算近似,自适应步长梯度下降姿态解算与高精度惯导数据误差对比,PIT轴为2.12%,ROL轴为1.95%。

图8 弱动态下姿态解析对比Fig.8 Analytical comparison of attitude under weak dynamics

图9为强动态下姿态解析对比,由于传统梯度下降姿态解算每次迭代步长固定,当机身运动角速度大于30 (°)/s的强动态条件时姿态变化较快,迭代不能及时跟随响应,导致姿态解算存在一定时延,且在端点处不能反馈真实姿态信息。定步长梯度下降姿态解算与高精度惯导数据误差对比,PIT轴误差为9.11%,ROL轴误差为8.68%;自适应步长梯度下降姿态解算与高精度惯导数据误差对比,PIT轴误差为2.31%,ROL轴误差为2.14%。

图9 强动态下姿态解析对比Fig.9 Analytical comparison of attitude under strong dynamics

4 结论

本文以旋翼无人机强动态高速运动背景下提高低成本MEMS传感器姿态解析精度、降低时延为核心思想,分析并校正传感器原始数据误差,在强动态运动条件下确定传感器量程范围后设计二阶巴特沃斯低通滤波器,并用零相位时延修正方法削弱因滤波器相位偏移导致的时滞,在72 MHz处理器中设计自适应步长梯度下降姿态解算方法,根据运动状态估计因子大小自适应调整迭代步长。实验结果表明该解算方法在强动态条件下姿态解算精度更高、时延更小,可为无人机提供准确姿态信息,具有一定的实际工程应用价值。