低频振动环境下压电能量转换装置响应特性

梁梦凡,李福松,金功伟

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

传统意义上,微机电系统(MEMS)和无线传感网络(WSN)节点供电主要依赖于化学电源[1]。化学电源可稳定、高效地对电能进行直接存储或释放。然而,在特殊工作环境下,化学电源存在体积大、工作周期有限和需定期人为更换等缺点。考虑到MEMS和WSN器件低能耗的特点,微能量收集装置应运而生[2]。相比于传统的电池供电,能量收集器具有特殊环境匹配性高、长寿命和小体积等优点,被广泛应用于健康检测[3]、传感[4]、医疗器械[5]和环境检测[6]等领域。能量收集器利用电磁效应、静电效应或压电效应等将外部激励(风能、机械能和电磁能等)转化为电能输出,常见的有摩擦纳米发电机(TENG)[7],电磁发电机(EMG)[8]和压电纳米发电机(PENG)[9]等。振动能是生活中常见的机械能量之一,可由飞机机翼、发动机引擎和运输装作业等过程产生,因此,研究振动能量收集器对解决特殊环境下低功耗器件能源保障问题具有重要意义。其中,压电式能量收集器(PEH)由于结构简单、抗电磁干扰和小尺寸等优点逐渐成为研究热点之一[10-12]。

虽然前人对PEH装置做了大量研究工作,提出了许多具有新颖结构的压电收集器,但多数研究局限于单因素优化策略。压电发电的功率密度较高,发展趋于MEMS化,对于悬臂梁结构的PEH器件转换电路多为标准整流电路,因此该结构设计过程存在的不足有：1) 收集器体积较大,一阶振动频率较高,难以应用于低频环境;2) 收集器振动结构使压电材料的工作模式单一,不能有效收集多振动模式下的能量等。因此,针对典型应用场景如周围震动环境实时检测、触摸设备能量回收和智能穿戴自供能等,外界环境的振动随机性和非线性对能量收集器的材料参数、外接负载大小、结构刚度和装置尺寸提出更加苛刻的设计要求,只有不断优化压电能量收集装置的结构才能最大程度提高其输出性能和可靠性。针对低频振动环境下微功耗电子器件结构与性能关系不明确问题,通过有限元方法探究压电微能量收集装置多参数对其输出响应特性的影响,为设计新型能量收集装置和电能源转换技术提供一定的指导作用。

1 PEH工作原理

1.1 压电方程

传统PEH装置原理主要运用以压电材料作为核心结构的压电方程,在一定边界条件下,通过电位移矢量(D)、应力张量(T)、电场强度(E)和应变张量(S)四种物理量将力-电关系以数学形式表现出来。其中,边界条件可分为电学和机械两类,根据约束条件的不同,方程类型和适用场合也不同。机械约束条件分为自由和夹持两种,对应的方程在电学中分别为开路和短路,在特定条件下,机械-电学方程可以实现相互转换,两种机械条件和两种电学条件情况结合而组成四种不同情况,分别对应①～④类。只有在满足对应的约束条件下压电方程才成立,同时也只反映在对应约束条件下所对应的各物理量关系,具体参数如表1所示。

表1 压电方程参数对应情况Tab.1 Parameter description of piezoelectric equation

此外,压电材料在工作过程中通过振动产生的纵向、横向应力作用于压电片上从而有效输出电能,该工作模式下压电材料受外力,压电片边界被束缚不能发生自由形变,符合机械夹持条件,而再无电场力作用但电位移矢量不为零时,电势能由机械能转换而来,此时满足电学短路的约束条件,因此本文选择第②类条件。

对于PZT压电材料而言,d31耦合模式下产生的形变大于d33耦合模式,因此PEH采用d31机电转换模式,旨在通过最低的成本,最大程度地提升该装置的综合输出性能。

1.2 机电耦合模型

图1(a)所示为PEH装置结构示意图,由支撑材料、压电材料、振动质量块和固定支座组成,通过系统振动可带动压电材料沿y方向往复运动,压电材料的极化强度矢量P平行于y轴。图1(b)所示为悬臂梁压电振子等效结构图,两层压电材料负极与负极相连,正极与正极相连,压电层的极化方向相反。该结构体系下,质量块M受自身重力作用,同时存在机械结构刚度系数Ks、阻尼系数Cs和压电材料引起的外界激励Fp。因此,系统的机械方程可表示为

(1)

图1 压电能量转换装置模型Fig.1 Piezoelectric energy harvester model

文献[13]研究表明,PEH装置可等效为电流源与负载并联,因此,根据基尔霍夫定律可知

(2)

联合式(1)和式(2)可得到负载为等效电阻时系统的机电耦合方程,求解该方程组即可得压电能量收集器机械参数与输出性能关系,并探究体系结构(质量组成、压电材料比重和结构刚度等)对压电发电机响应特性的影响。

2 PEH响应特性

2.1 PEH有限元仿真

压电材料作为PEH装置最核心部件,其性能直接影响系统的输出电性能,常见的压电材料性能参数见表2[14]。

从表2数据可知,锆钛酸铅(PZT)材料具有较大的压电系数和较高的机电耦合系数,作为一种较理想的压电材料,被广泛应用于压电装置,因此本文选择PZT为压电材料。为了在有限元模型中得到良好的受力效果,本文的支撑材料和质量块均选择结构钢[15]。通过Comsol 5.2软件构建的图1(a)结构有限元模型参数见表3。

表2 常见压电材料参数[14]Tab.2 Parameter description of piezoelectric materials

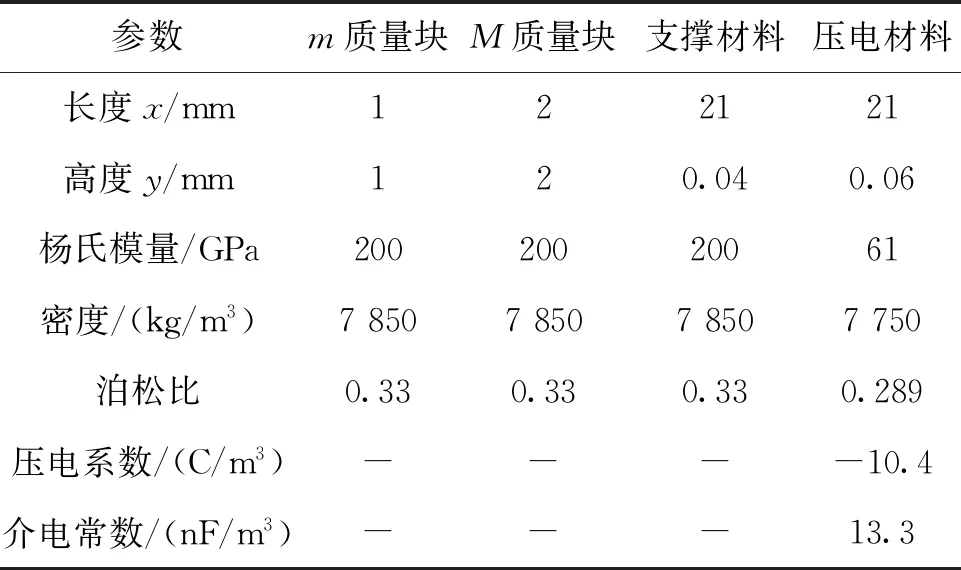
表3 有限元模型参数Tab.3 Parameter description of finite element model

图2 压电能量转换器有限元模型Fig.2 Finite element model of PEH

为了简化计算,本文采用频域响应求解器分析二维结构模型,利用表3参数进行建模得到的初始结构(对照模型)PEH装置几何形状如图2所示。设置初始负载R为10 kΩ,正弦激励加速度为1g,面外尺寸设置为14 mm[16],支撑材料和压电材料阻尼类型简化为各向同性,损耗因子均设置为0.001,通过定义接地端口和终端实现图1(b)所示的等效电路,频域参数化扫描范围设置为71～91 Hz,模拟步长为1 Hz,容差最大迭代次数设置为25,容差因子和残差因子分别设置为1和1 000。

图3为PEH装置响应特性。由图3(a)和3(b)可知,该装置的有效响应频带为75～88 Hz,且随着外界激励频率的增加,PEH装置的输出电压和功率均呈现出先增加后减少的趋势。当外界激励频率为81 Hz时,PEH的输出电压和负载功率均达到最大值,分别为3.58 V和 0.64 mW,此时激励频率与系统固有频率一致。在系统固有频率附近,输出电压和功率都呈现出类似对称的变化过程。为了分析PEH最佳工作状态时的响应特性,图3(c)为81 Hz时PEH输出电压和功率随负载电阻的变化。仿真结果表明,随着负载电阻从102～105Ω变化时,输出电压呈现出先迅速增加后缓慢趋于3.86 V稳定电压的增长趋势;同时,PEH的输出功率随外接负载先增大,达到最大值(R= 3 162 Ω,P= 0.96 mW)后减小。PEH输出功率可表示为

(3)

式(3)中,ω为谐振频率,a为加速度。

图3 PEH响应特性Fig.3 Response characteristics of PEH

根据式(3)可知,当外接负载与内阻电路相等时,即R=π/(2Cpω)=3 162 Ω,此时PEH达到最佳工作状态。因此,在设计PEH装置时,需根据内部等效电阻情况添加合适的负载电路,若所配负载过小,两端电压和功率都很小,若负载电阻远大于等效电阻,电路中电流过小会导致装置功率低。图3(d)为输出电压和功率随加速度激励的变化情况,由图可知,加速度由0.25g增加到4g时,对应的输出电压(功率)分别由0.89 V(0.04 mW)增加到14.3 V(10.26 mW)。值得注意的是,在谐振频率下(81 Hz),输出电压随加速度呈线性相关,而功率与加速度呈二次函数关系。

图4为PEH装置在不同频率下工作的效果图,可以看出在共振频率处端口处压电材料表面的电势最大,因此可在负载两端产生最大的输出电压,与上述分析结果一致。

图4 PEH装置工作效果图Fig.4 A working renderings of PEH

2.2 PEH特性分析

2.2.1传感质量块对PEH响应特性的影响

保持其他输出参数与建模条件不变的情况下,通过改变传感质量块的大小(质量),分析重量对PEH输出响应特性的影响,模拟结果如图5所示。图5(a)为在外接电阻为10 kΩ,加速度大小为1g时,不同尺寸末端质量块的频率响应关系,随着质量块边长(a∶b)由1∶1增加到1∶4时,有效响应频带由118～142 Hz降低为40～52 Hz,PEH体系的固有频率逐渐降低,输出电压逐渐增大从开始的131 Hz(1.88 V)过渡到最终的46 Hz (10.07 V),同时曲线形状也更为陡立。因此,通过改变外部质量块的重量,不仅可以降低PEH固有频率和能量转换效率,还可以调整装置对振动频率的敏感特性。在PEH系统中,外接负载阻抗匹配可有效增加能量输出,图5(b)为电压和功率(内插图)随外部负载响应关系,不难看出,不同质量比时,输出电压随电阻的变化相一致,呈现出先迅速增加后变缓慢并趋于平衡的趋势,当负载电阻为10 kΩ时,不同质量比对应于不同的稳定电压,质量比为1∶4时产生的电压(11.32 V)比1∶1时(2.44 V)提高了3.6倍。同时,随着负载电阻由102Ω增加到105Ω,不同质量比下,每个PEH存在对应最佳负载值,并在此达到输出功率最优。图5(c)为不同质量比下加速度响应规律,由图可知,输出电压和输出功率与加速度(合外力)分别呈现出线性和二次函数关系,随着外部激励的增加,输出电压和功率均增加,该曲线也能从侧面反映电压和输出功率关系。

图5 质量分布对PEH的影响Fig.5 Effect of mass distribution on PEH

2.2.2质心分布对PEH响应特性的影响

为了探究传感质量块质心分布对PEH响应特性的影响,在保证传感质量块体积不变的情况,改变其形状(质量块长宽比分别设置为1∶4、2∶2和4∶1),分析质心分布对PEH装置响应特性的影响。图6(a)所示为输入加速度激励为1g,外接电阻为10 kΩ时,可看出质量块长宽比从1∶4增加到4∶1时,整个体系的固有频率逐渐降低,从87 Hz下降到78 Hz,降低了10.34%,此时,输出电压不断增高,从3.50 V增高到3.62 V,增高了3.43 %。图6(b)所示为输出电压和输出功率随外接负载的变化,可以看出不同质心分布下,输出功率随负载变化曲线具有相同的变化趋势,长宽比从1∶4与2∶2时具有相同的系统等效负载,即5 623 Ω时体系输出性能最优;当长宽比为4∶1时,输出功率在3 162 Ω时达到最大0.92 mW。观察输出电压变化曲线可知,除了陡变区域(103～104Ω)有细微差别外,保证相同体时,不同质心分布对电压的影响并不明显,此规律也可体现在图6(c)中。当外界激励从0.25g增加到4g时,三种形状的传感质量块的输出电性能对加速度响应规律相同。由上可知,当系统质量恒定而改变其质心分布时,可以使整个系统的共振频率发生改变,同时质心分布对体系输出电压不敏感,因此在特定工作情况下,可在保证整体质量不变而改变传感质量块形状以满足应用要求。

图6 质心分布对PEH的影响Fig.6 Effect of distribution of the center of mass on PEH

2.2.3压电材料厚度对PEH响应特性的影响

PEH装置的能量最优化设计中,除了关注系统本身结构的设计外,还需要注重核心压电部件对整体性能的影响,当选定所需压电材料后,其薄膜厚度会明显影响PEH输出电性能。图7所示为不同厚度压电材料对PEH装置输出响应特性的影响。由图7(a)可知,当电压厚度由0.03 mm增加到0.09 mm时,输出电压的振幅逐渐较小,其变化趋势与输出功率相似,是系统的刚度增大所致,导致压电单元的应变降低。PEH谐振频率由41.06 Hz右移至125.44 Hz,同时,负载电压峰值由4.62 V降至3.26 V,输出功率峰值由1.09 mW降至0.47 mW。由图7(b)可知,随着压电材料厚度增加,PEH装置的最大输出功率呈现减小趋势,由1.35 mW降低至0.52 mW,同时,阻抗匹配度也随之变化,负载的改变可导致能量耗散程度变化。图7(c)所示为PEH在不同厚度时的加速度相关性,与上述分析结果一致,输出电压和输出功率随外加激励分别呈现线性和二次函数关系,且随着厚度增加,体系加速度响应的敏感性逐渐降低。因此,在保证压电材料承重强度下,适当地选择较薄压电层,可在低频谐振频率下获得更高的峰值电压和更好的传感灵敏度。

图7 压电材料厚度对PEH的影响Fig.7 Effect of thickness of piezoelectric material on PEH

2.2.4压电材料分布对PEH响应特性的影响

不同工况会对悬臂梁式PEH的力学强度提出不同的要求,压电材料作为压电发电机最核心部件,分析其在振动臂上的分布对装置输出响应尤为重要。本文在确保支撑材料厚度一定,且支撑材料长度与压电材料长度比为1∶1时,探究压电材料的分布位置对PEH装置的影响。根据图8(a)可知,压电材料由靠近固定端(左侧)到振动收集端(右侧)时,体系的谐振频率由83 Hz右移至124 Hz。值得注意的是,压电材料在右侧时体系的峰值电压(5.78 V)明显高于其在左侧(5.00 V)和中间(3.86 V)。由图4可知,靠近振动能量收集侧的悬臂梁形变最严重,因此,可推测当压电材料趋于右侧分布时会使体系的能量转化效率明显提升。由图8(b)可知,随着压电材料向振动收集侧分布,最大功率由0.96 mV增加到2.23 mV,增加了133%。此外,压电材料的分布并不改变体系的阻抗匹配,且随着负载由102～105Ω变化时,在3 162 Ω前,输出电压随外界负载的变化趋势基本相同,且变化大小无明显差别,当负载超过体系等效电阻时,靠近振动能量收集端的体系输出电压随负载变得明显。图8(c)所示为外加激励对PEH装置输出功率的影响,与上面分析的一致,当压电材料靠近振动收集端时,体系对加速度的响应特性更加明显。因此,在不改变悬臂梁长度的前提下,适当增加振动收集端的压电材料分布,能显著提高PEH装置的能量转换效率和传感灵敏度,同时,在相同振动模式下,体系最大功率处负载不随压电材料分布变化而变化,更有利于振动系统对外界能量的收集。

图8 压电材料分布对PEH的影响Fig.8 Effect of distribution of the piezoelectric material on PEH

3 验证

为验证有限元仿真对PEH结构影响特性分析的有效性和正确性,本文将理论分析结果与实验室成果进行比较。文献[16]设计的悬臂梁式PEH结构如图9所示。

图9所示的PEH装置由传感质量块、双压电晶片、铝支架和固定基座组成,其中双晶压电材料尺寸为20 mm×14 mm×0.16 mm,与表3所取的参数一致,为了减少二维模型对模拟结果的差异,本文设置面外尺寸为0.16 mm,与该装置保持一致。铝支架固定在一个模拟环境振动的电磁激振器上,虽然实际PEH结构(图9(a))和图9(b)中给出的(弹簧,质量,阻尼器)模型看起来不同,但在谐振频率附近,该机电耦合模型可准确地描述PEH的振动行为。

图9 PEH装置示意图[16]Fig.9 Piezoelectric generator[16]

图10为本文有限元仿真结果与文献[16]实验室测试结果的比较,不难看出,文献[16]测试得到的体系谐振频率为66 Hz,最大输出功率为0.57 mW,小于本文计算的结果,同时,文献[16]得到的输出功率在13.9 kΩ时达到最大0.58 mW,同样小于本文的计算值。虽然较实验测试数据有所偏差,但本文计算得到的响应特性变化趋势与文献[16]的结论相吻合。由于文献[16]所取传感质量块的质量为0.76 g,而本文并未对质量定值,而是将其作为单位变量进行分析,因此本文设置的等效质量块质量小于文献[16],这也证实了质量分布对PEH的影响规律。为了减少模拟参数误差对整体性的影响,本文的支撑架为结构钢,而非文献[16]所述的铝。同时,由于本文所建立的模型为二维等效结构,无法得出与实验完全一致的结果。综上考虑,本文的计算结果可以较为有效地反映PEH结构参数对其能量转换性能的影响特性,可为微结构能量转换装置的研究提供一定的设计指导和借鉴作用。

图10 响应对比Fig.10 Comparison of response results

4 结论

本文通过有限元方法,探究了不同设计参数下振动频率、外界负载和外部加速度激励对压电能量收集装置输出电性能的影响。仿真结果表明,传感质量块质量的增加伴随着负载电压和负载功率的增加,但保持质量块体积一定时,改变其形状可达到通过控制质心分布来调控PEH装置的输出响应;同时,随着压电材料厚度增加,系统的刚度增大导致压电单元的应变降低,使得PEH装置的最大输出电压和功率降低;压电材料趋于振动收集侧分布时会使体系的能量转化效率明显提升。在负载阻抗方面,改变PEH装置的结构分布都会对系统最佳负载值有影响,然而,只改变压电材料分布时,最佳负载值无明显变化。对外部激励方面,输出电压和输出功率与加速度(外力)分别呈现出线性和二次函数关系,且随着外部激励的增加,输出电压和功率均增加,因此,可通过改变外力情况调控PEH的加速度响应范围和灵敏性,由于本文模型具有较大的横纵比,对纵向振动响应更为敏感。然而单方向振动模式并不能满足实际振动环境的随机性要求,因此,在单因素到多因素优化策略的同时,也需要从单维度到多维度设计,达到拓宽PEH装置工作频带和提高其输出稳定性的目的。