基于数值模拟方法的中心起爆战斗部破片动态飞散特性研究
2023-07-12金贺龙万早燕
谭 波,金贺龙,张 俊,苗 润,万早燕
(1.海军工程大学兵器工程学院,湖北 武汉 430033;2.西安机电信息技术研究所,陕西 西安 710065;3.海军研究院,北京 100161 )
0 引言
引信与战斗部的配合问题最早起源于二战期间。随着近炸引信的出现,在弹道飞行期间选择一个最合适的炸点,使战斗部对目标的毁伤效能最大,就开始成为武器系统设计者关心的问题。在弹目交会过程中,由引信所控制的炸点与战斗部毁伤元的配合效果,决定了武器系统作战任务的完成,因此引信与战斗部的配合问题就显得异乎寻常的重要。
破片战斗部是现役装备系统中最主要的战斗部形式之一。在现有的引战配合条件下,破片战斗部对目标的毁伤具有更为广泛的适应能力,常用于攻击地面、水上和空中的军事目标以及人员等有生力量。就破片战斗部而言,战斗部与引信配合问题,就是引信启动区域与战斗部破片动态飞散区域的协调性问题;为了设计引信的启动区域,首先要研究战斗部破片的空间飞散特性,进而指导武器系统的引战一体化设计。
长期以来,对于破片战斗部的破片飞散参数和毁伤效应的研究主要借助于试验测试手段;近年来,随着计算机数值仿真技术的广泛应用,为战斗部作用过程毁伤元物理特征细节的研究提供了可能,已成为一种不可或缺的研究手段。近些年来,一些学者对战斗部破片飞散特性开展了大量的研究工作,取得了一系列的研究成果。文献[1]通过改进战斗部内衬结构来提高战斗部破片的轴向杀伤威力,并通过数值模拟与试验验证相结合的方式对此类战斗部破片的飞散特性进行研究。文献[2]构建了中空型战斗部破片初速的计算模型,并通过有限元分析软件对采用一端环形起爆与多点起爆的中空型战斗部破片成型过程进行了数值模拟。文献[3]总结了国内外战斗部破片速度测量方法,并对各种测量方法的优缺点进行了较为详细的对比分析,在此基础上重点探讨现有破片速度测量方法中存在的问题。文献[4]采用修正后的破片初速理论计算破片初速,并通过有限元计算模型对战斗部爆炸情况下破片的运动状态进行研究,得到破片飞散轨迹与破片空间分布等特征参量。文献[5]设计了一种阵列式光幕靶测试系统,并将该测试系统用于战斗部外场破片动态试验,结果表明,列阵式光幕靶能够精确测量5 mm小尺寸破片速度以及破片群的分布规律。文献[6]采用有限元计算方法对复合装药战斗部的破片特性进行研究,重点分析中心单点和内外点同时起爆两种作用方式的战斗部壳体破碎与爆轰波传递过程,以及壳体壁厚和装药直径变化对形成的战斗部破片特征参量的影响。文献[7]采用数值模拟计算和试验验证相结合的方式对内刻槽半预制战斗部的破片成型规律进行研究,重点分析横纵向刻槽的形状、深度等参量对破片成型的影响。此外,文献[8—9]也对不同类型战斗部的破片飞散特性开展了研究。总结前人的研究可知,对于破片飞散特性的探索,较为常见的是基于有限元仿真与战斗部静爆试验的破片静态飞散特性研究,战斗部静态飞散特性的研究只能解决战斗部径向一定范围内破片飞散特性问题。但现实中战斗部通常处于运动状态,由于战斗部存在牵引速度,其破片实际飞散特性是破片静态飞散与战斗部牵引速度的叠加,相关研究报道相对较少。并且破片动态飞散特性是战斗部毁伤性能研究的核心内容,因此有必要开展深入细致的研究工作,进而满足引战一体化设计的需求。
本文以采用中心点起爆方式的常规战斗部结构为研究对象,采用数值模拟方法对此战斗部破片的空间动态飞散特性开展深入研究,重点分析不同时刻、不同工况破片速度与破片空间分布特性,为作战目标的高效毁伤以及引信与战斗部的一体化设计提供依据。
1 破片飞散特性的数理模型
1.1 破片动力学方程
战斗部起爆后,其破片获得一定的初始速度,脱离爆轰产物的作用后在空中飞行,此时破片会受到重力和空气阻力这两种力的作用。
根据牛顿第二定律,破片运动的动力学方程表达式为
(1)
式(1)中,m为破片质量,kg;CR为空气阻力系数;ρa为空气密度,kg/m3;v为破片速度矢量,m/s;A为破片飞行方向上的特征面积,m2;g为当地重力加速度,m/s2。对于预制的球、圆柱体等形状破片,其特征面积A的表达形式为
(2)
式(2)中,S为破片的表面积。
由于破片在空中飞行时会不断翻滚,因而除球形破片外,其他形状破片的特征面积一般是随机变量,此时破片特征面积可采用数学期望的形式进行表达
A=φm2/3,
(3)
式(3)中,φ为破片的形状系数。
1.2 空气阻力系数
由破片运动的动力学方程(1)可知,破片在空中飞行会受到空气阻力的影响,空气阻力系数CR是表征破片速度衰减状态的重要特征参数。根据空气动力学相关原理可知,破片的空气阻力系数CR值主要取决于破片速度与形状。CR值通常可以通过风洞试验和数值仿真计算等手段得出。一些学者对于破片空气阻力系数[10]开展了较为系统和深入的研究工作。文献[11—12]给出了立方体形破片在不同破片飞行马赫数区间下的空气阻力系数,如表1所示,本文空气阻力系数采用此项研究成果。
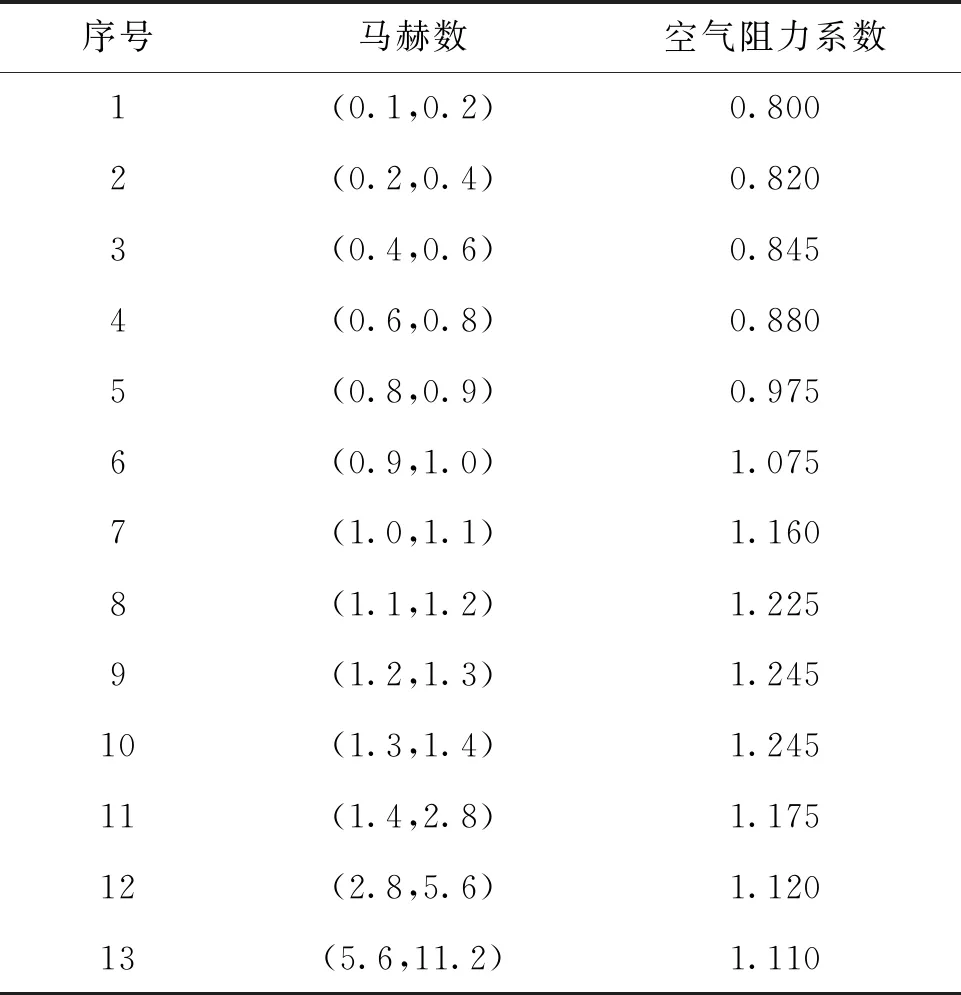
表1 立方体形破片空气阻力系数Tab.1 Air drag coefficient of cubic fragments
1.3 静态破片初速轴向分布
战斗部装药两端的稀疏波与战斗部起爆位置及起爆方式都会对破片静态的轴向初速分布产生影响,端部效应使得战斗部中间部分破片初速高于两端的破片初速,相关领域的精确计算极其复杂。为了简化研究,本文采用前人的研究成果,直接给出圆柱形战斗部在中心点起爆方式下破片初速沿轴向分布的计算公式[13]
(4)
式(4)中,L为战斗部装药长度,d为战斗部装药直径;x为计算微元离基准端面的距离;v0x为x处的破片初速,v0s为静态破片初速。
1.4 单枚破片飞散方向角
破片飞散是战斗部对目标杀伤的一种重要方式,其特性是战斗部毁伤效能评估的重要参量。破片飞散特性决定了破片的空间分布和破片的空间密度,而单枚破片飞散方向角的计算又是破片场空间分布计算的基础。当破片飞离战斗部壳体时,通常会朝着爆轰波前进的方向倾斜某一角度,对于单枚破片的飞散方向常采用较为成熟的泰勒方法进行计算[13-15]。由于本文研究的战斗部采用中心点起爆方式,此种起爆方式有利于形成更大的破片飞散角度。
计算破片飞散方向的泰勒公式为
(5)
式(5)中,δ为计算微元的飞散方向与该处壳体法线方向的夹角;α为爆轰波阵面的法线与弹体轴线之间的夹角;D为主装药爆速。
2 破片动态飞散特性数值方法
本文第1章介绍描述破片运动的基本方程及其特征参量的表达形式,本章在此基础上研究中心起爆战斗部破片动态飞散特性的数值计算方法。
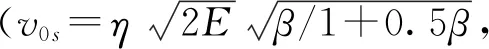
本文研究的常规圆柱形战斗部结构如图1所示,战斗部预制破片采用某金属材料、单层预制破片结构;预制破片轴向布置32个,环向均匀布置30个,共960个;单枚破片形状与质量相同,采用立方体形状,破片质量8 g;战斗部直径为130 mm,战斗部主装药采用某型炸药,采用中心点起爆方式。战斗部初始运动速度v0M,沿弹体轴线方向;另假设战斗部不同位置破片静态初始速度值v0x只沿弹体轴线方向发生变化,其可根据Curney公式计算,并用公式(4)修正得到,计算结果如图2所示。由此可知,战斗部中间部位破片的静态初速大于两端的破片初速,并且战斗部中心部分主要区域破片静态初速约为1 200 m/s。当战斗部转速不高时,破片所受环向速度相对于轴向与径向速度是个小量,因此本文在研究战斗部破片飞散特性时,忽略环向速度的影响。则破片的动态飞散速度v是破片静态飞散速度vs和弹体速度vM的合成。
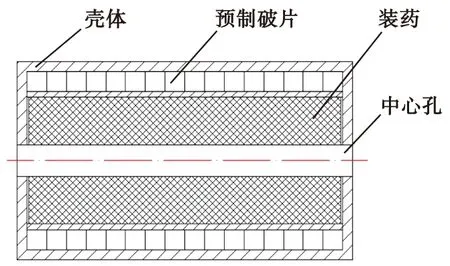
图1 战斗部结构示意图Fig.1 Schematic diagram of warhead structure
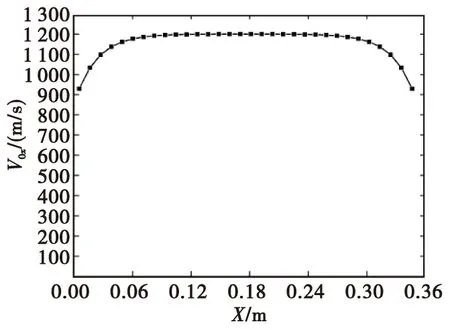
图2 破片静态初速分布曲线Fig.2 Fragmentstatic initial velocity curve
对于破片的运动轨迹采用运动学方程进行描述,其表达式为
(6)
式(6)中,X为破片运动矢量。将式(1)和式(6) 联立,组成描述破片运动完备方程组
(7)
定义地面坐标系Axyz,坐标系原点A取在战斗部中心,Ax轴沿水平线指向弹体飞行方向,Ay轴铅直向上,Az轴按右手法则确定。弹轴坐标系Ox′y′z,坐标系原点O取在战斗部中心,Ox′轴与弹体纵轴重合,指向头部为正;Oy′轴位于弹体纵向对称面内,与Ox′轴垂直,向上为正;Oz轴垂直于其他两轴并构成右手坐标系。将破片运动动力学方程在弹轴坐标系Ox′y′z上分解,同时将破片运动学方程在地面坐标系Axyz上分解,这样破片速度矢量表示为v=[V′x,V′y,Vz]T,破片运动矢量表示为X=[x,y,z]T,对于任一变量采用龙格-库塔方法进行求解。
对于一阶微分方程
dx/dt=f(t,x)。
(8)
若已知tk时刻的参数值xk,则可用龙格-库塔法求tk+1=tk+h时刻xk+1的近似值。对应的四阶龙格-库塔公式为
(9)
(10)
在数值计算开始时,需对战斗部每一枚破片进行初始化参数赋值,初始化参数包括战斗部起爆时刻任一破片在地面坐标系Axyz中的x、y、z位置参量,以及战斗部任一破片的合速度在弹轴坐标系Ox′y′z下的速度分量Vx′、Vy′、Vz。
3 计算结果与分析
3.1 破片飞散特性分析
采用第2章数值方法,对弹体初速v0M为700 m/s,飞行高度50 m,弹体水平飞行工况的战斗部破片动态飞散特性进行研究,得到不同时刻破片飞散场如图3所示。由图可知,不同时刻破片场的飞散区域呈现一种近似的圆环结构,并且在垂直于弹体轴线方向,随着飞行时间的增加,破片毁伤径向区域的范围逐渐扩大;同时破片群的轴向影响范围也在逐渐增加。破片径向范围的扩大由径向初速所致,而对于破片群轴向区域扩大的现象可做如下解释。本文研究的战斗部采用中心点起爆方式,壳体区域预制破片沿中心点对称排列,使得不同位置破片与中心点的连线不同。根据泰勒和夏皮洛等人的研究,当战斗部起爆后,破片总是朝着爆轰波前进方向倾斜某一角度飞离战斗部壳体。不同位置破片飞散角沿中心点向两侧逐渐增加,使得破片向战斗部两侧飞散开来,随着飞行时间的增加,破片轴向区域的影响范围也逐渐扩大。
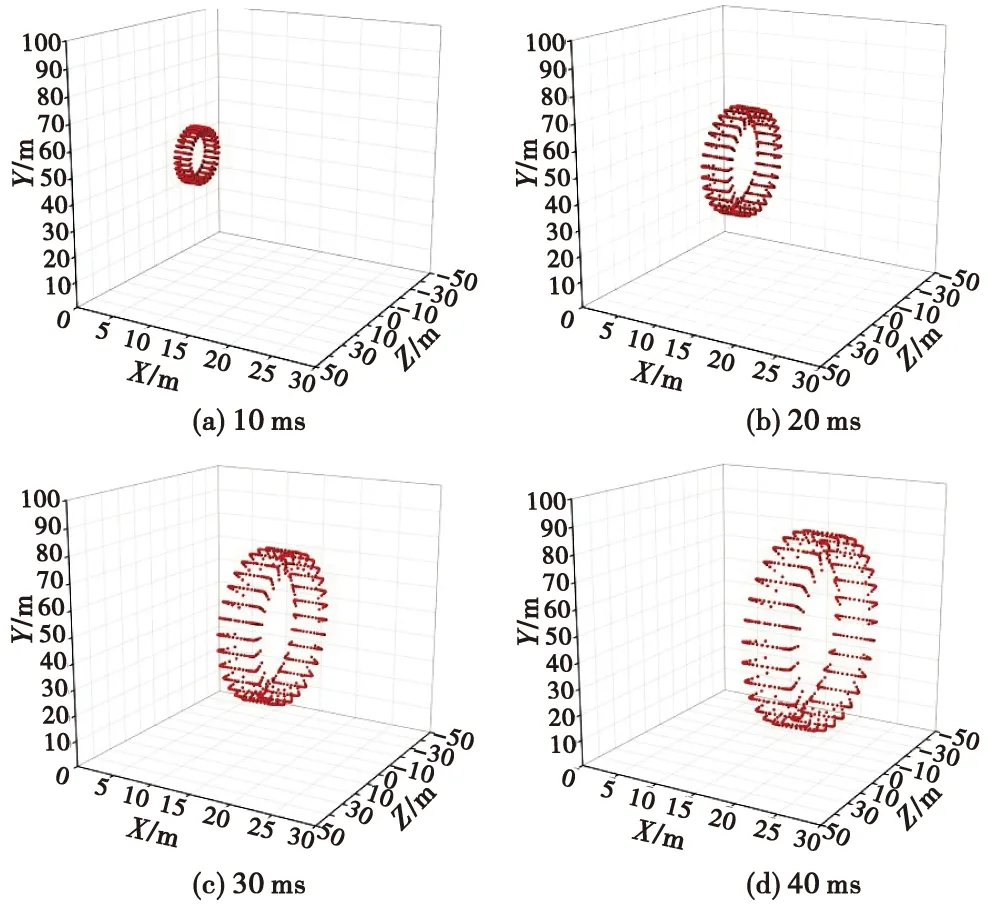
图3 不同时刻破片飞散场Fig.3 Fragment scattering section at different times
由于破片沿战斗部轴线呈现等角度的圆周对称分布,因此在环向均匀布置的30组破片中选一组为研究对象。定义破片飞散半径为破片当前位置与弹轴线之间的距离;以起爆位置战斗部中心点为原点O,弹轴为坐标轴OA,沿径向指向选定破片方向为R轴建立坐标系,则不同时刻破片飞散区域分布如图4所示。通过观察图4可知,不同时刻破片飞散基本分布在以战斗部初始中心位置为原点两条射线之间的区域,该区域也对应此行破片的动态飞散方向。由于战斗部破片分布具有沿轴向等角度对称特性,对应于三维空间,破片飞散区域就是以战斗部初始中心位置为原点,对称于弹体纵轴的空心锥结构,该空心锥区域也就是战斗部破片的杀伤区域。随着破片飞离战斗部表面,该行破片的形状由弧形逐渐向U形过度。弧形结构由静态初速沿轴向分布所致,并且由于受到不同位置破片向前或向后飞散方向以及弹体牵引速度的影响,破片群形状最终呈现U形。并且,破片群在飞散过程中,沿轴线方向的影响范围也是逐渐增加的,与前面三维破片场呈现的规律一致。此外,随着破片飞散时间的增加,相同时间间隔内,破片群的运动距离逐渐减小,表明破片的飞行速度逐渐减小。
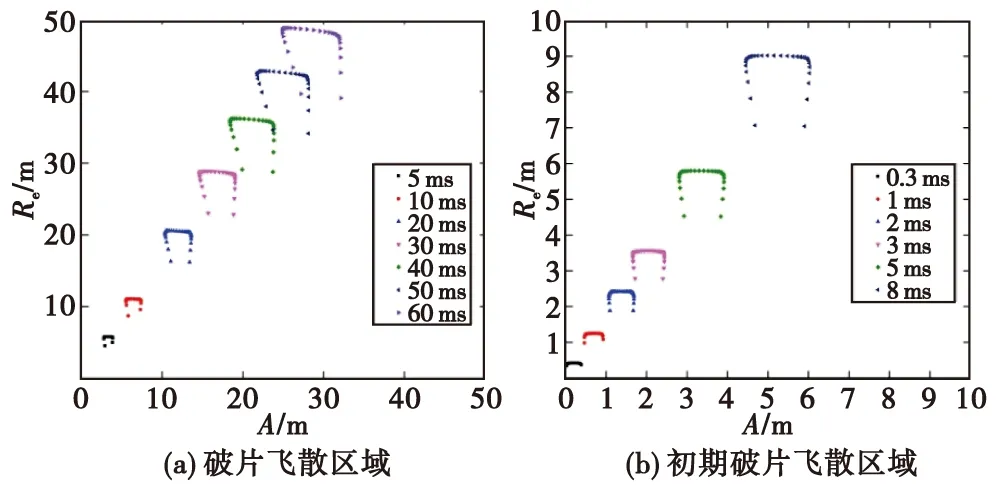
图4 不同时刻破片飞散区域分布Fig.4 Distribution of scattering fragments at different times
为了探索单枚破片的速度与飞散特性,取所研究对象破片群从战斗部左端起第12、18、24号破片进行研究。图5给出不同破片径向速度时间历程曲线。由图可知,当破片脱离爆轰产物作用后其运动速度开始衰减,随着飞散时间的增加,破片的径向速度逐渐减小。并且在飞散运动初期,破片径向速度衰减较快,但随着飞散时间的增加,破片径向速度的衰减程度逐渐变小。
根据式(1)以及相关理论,破片在空中飞散过程中会受到空气的阻力作用,空气阻力与破片速度的平方项成正比。初始阶段,破片速度较大,其承受的空气阻力也相对较大,使得破片速度迅速衰减,随着飞散时间的增加,破片运动速度减小,其受到的空气阻力也逐渐减小。
图6给出不同破片飞散半径随时间的变化曲线。同样,在破片飞散运动初期,破片飞散半径快速增大,表明此时破片的飞散速度较快;而随着飞行时间的增加,虽然破片飞散半径仍不断增大,但其增大程度却在不断变缓。同时,对比3枚破片飞散半径变化的历程可知,飞散运动初期3种工况破片飞散半径差异较小;当破片飞离战斗部30 ms后,3种工况破片飞散半径差异越发明显。在3枚破片中,靠前位置第12号破片的飞散半径最大;并且沿弹轴方向,另两枚破片的飞散半径逐渐减小。表明破片群中间部位的破片,沿着弹轴方向其飞散半径逐渐减小,此与图4呈现的不同时刻破片群飞散特性结果一致。当破片飞散40 ms后,3枚破片飞散半径分别为36.23 m、36.01 m、35.64 m。
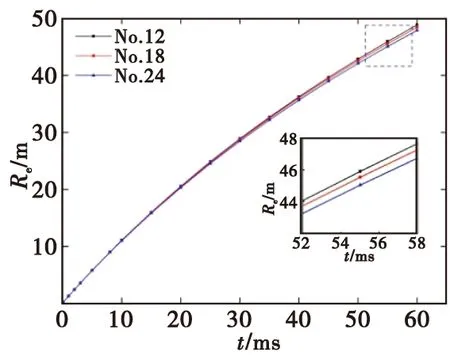
图6 破片飞散半径随时间的变化曲线Fig.6 Variation curve of fragment scattering radius with time
破片动能是反应破片做功能力的一个重要参数,通常破片的动能越大,其对作战目标的毁伤能力也越强。图7给出破片群破片平均动能随时间的变化曲线。由此可知,随着破片飞散时间的增加,破片的平均动能逐渐减小;同样,在飞散运动初期,破片动能衰减较快,之后随着飞散时间的增加,破片动能衰减程度逐渐变小。并且,当破片飞行46.5 ms后,破片平均存速约为735 m/s,对应破片动能为2161J;而使轻型装甲目标损伤的能量准则临界值为2158 J,表明此时破片对轻型装甲目标仍有毁伤能力,其对应的破片飞散半径约为40 m。
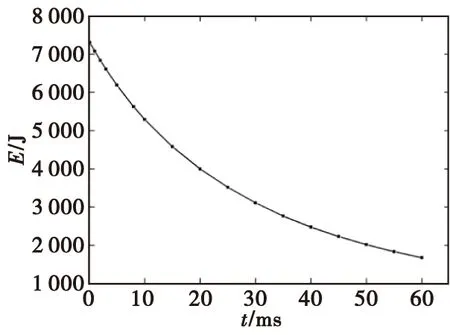
图7 破片平均动能随时间的变化曲线Fig.7 Variation curve of fragment average kinetic energy with time
3.2 质量变化对破片飞散特性的影响
为了研究破片质量变化对其飞散特性的影响,选取单枚破片质量5 g与8 g两种工况对比,同时不同工况破片形状、布置方位以及初速等特征参量相同,通过数值模拟得到不同质量工况破片飞散场如图8所示。对于不同质量的破片群,在破片初始飞散速度相同的前提下,破片质量越大,则同一时刻破片场的飞散范围越大,即破片的毁伤范围越大。表明当破片飞散速度相同时,增加破片质量,可以增强破片的空间飞散能力。
为了探索质量变化对破片速度与飞散特性的影响,选取破片组第18号破片为对象进行研究。图9给出不同质量工况破片飞散速度时间历程曲线。由图可知,当破片脱离战斗部作用后,随着飞散时间的增加,不同质量工况破片的飞散速度变化规律相同,都是在破片飞散运动初期,其飞散速度衰减较快,随着时间的增加,破片速度衰减程度逐渐变缓。并且,当破片飞散在3 ms内时,两种工况的飞散速度相差较小,随着时间历程的增加,两者飞散速度差异逐渐增大。破片质量越大,则破片在飞行过程中速度损失越小,其保存速度的能力越强;同一时刻,其破片余速越大。
图10给出不同质量工况破片飞散半径随时间的历程曲线。同样,在破片飞散运动初期,两种工况的破片飞散半径增大较快,随着时间历程的增加,破片飞散半径增大趋势逐渐变缓,两种工况变化趋势相同。此外,在破片飞散运动初期,不同工况飞散半径差异较小,随着飞散时间的增加,破片飞散半径差异逐渐增大;破片质量越大,同一时刻破片飞散半径也越大。
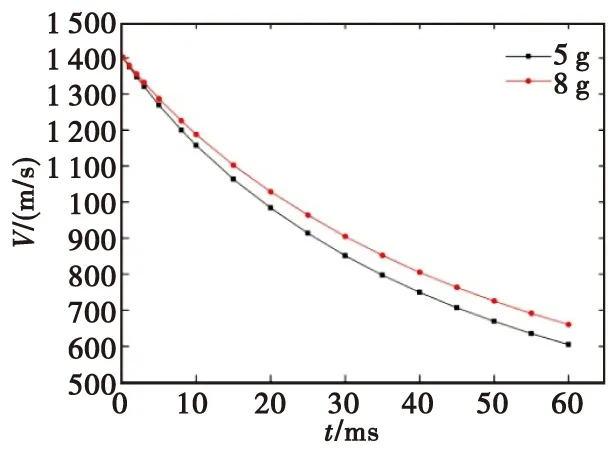
图9 不同质量破片速度时间历程曲线Fig.9 Velocity-time history curve of different mass fragments
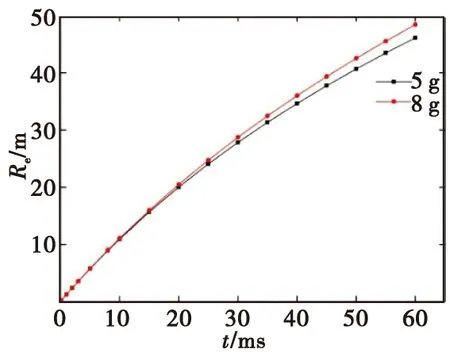
图10 不同质量破片飞散半径时间历程曲线Fig.10 Scattering radius-time history curve of different mass fragments
4 结论
本文以破片动力学基本方程为基础,建立一种研究中心点起爆方式战斗部破片动态飞散特性的数值计算方法。通过对不同时刻、不同工况破片速度与破片空间分布等参数的仿真与分析,得到如下结论:
1)当存在弹体牵引速度时,破片飞散呈现对称于弹体纵轴的空心锥结构。对于中心点起爆式战斗部,随着飞行时间的增加,破片场形状由弧形向U形转变,并且破片场的影响范围也在逐渐扩大。
2)当破片脱离爆轰产物作用后,随着飞散时间的增加,破片径向速度逐渐减小,飞散半径逐渐增大,但变化趋势都逐渐减小。质量8 g立方体破片在牵引速度700 m/s、飞散速度1 200 m/s作用下,破片飞散46.5 ms后,对轻型装甲目标仍具有毁伤能力,其飞散半径约40 m。
3)破片初始飞散速度相同,增大破片质量可以提高破片场的飞散范围。破片质量越大,则破片在飞行过程中速度损失越小,其保存速度的能力越强,破片的飞散也半径越大。
以上结论为指导引信弹药进行引战配合一体化设计,起爆控制策略优化、毁伤效能评估提供支撑。
