基于掺镱激光器的近单周期脉冲后压缩理论研究

程起 ，袁浩 ，曹华保 ，付玉喜

（1 中国科学院西安光学精密机械研究所 阿秒科学与技术研究中心，西安 710119）

（2 中国科学院大学，北京 100049）

0 引言

超短激光脉冲可以产生与原子势相比拟的光电场强度，成为研究非线性光学和强场物理的重要工具。其中，通过飞秒激光驱动的高次谐波过程产生阿秒光脉冲已经成为强场物理研究的重要课题。阿秒光脉冲可以从根本上认知微观世界相互作用与相对运动规律，进而从根本上揭示物质的宏观属性，因此受到了原子分子物理、量子物理、材料、医学等领域的广泛关注［1］。

目前钛宝石激光器是广泛采用的产生极紫外波段阿秒光脉冲的驱动光源，但是由于热效应的限制，基于钛宝石晶体的飞秒激光器平均功率小于50 W，进而限制了阿秒光源的亮度。然而随着阿秒光源应用范围的不断扩大，具有更高重复频率和更高亮度的阿秒光源需求愈发迫切，例如开展电子和离子态的符合测量［2］、探测固体材料能带结构动力学过程［3］、时间分辨的光电子发射显微成像［4］等研究，通常30 kHz到数MHz的高重频、高亮度的阿秒/飞秒光脉冲是比较理想的光源。为了获得短脉宽、高重频、高脉冲能量的驱动光源，研究人员开始将目光转向掺镱激光器。掺镱激光器（例如Yb∶KGW，Yb∶YAG）在近年来发展迅速，中心波长在1 030 nm附近，通过将激光晶体设计为板条或薄片来优化散热，最高可以获得千瓦级高平均功率的激光输出［5］。此外，由于基于高次谐波方法产生阿秒光源的效率与驱动激光波长λ-5、λ-6成正比，使用其二倍频（515 nm）激光能够大幅度提升极紫外波段阿秒光源的产生效率［6］。然而掺镱激光器的脉宽往往较大，在百飞秒量级，如基于Yb∶KGW晶体的激光器输出脉冲宽度可以达到190 fs（ Light Conversion 的pharos系列），基于Yb∶YAG晶体的激光脉冲为500 fs（Trumpf的dira系列），这样的脉宽无法用于产生孤立的阿秒光脉冲。

基于脉冲后压缩是被广泛采用的获得少周期超短激光脉冲的有效途径，目前常用的后压缩方法包括多程腔压缩、固体薄片组压缩、激光成丝自压缩和空芯光纤压缩等。多程腔压缩是近些年发展起来的新技术，具有小型化、简单、高效率等特点，例如HARITON V等利用装有熔融石英板的多程腔将倍频得到的515 nm脉冲压缩到了38 fs［7］。固体薄片组压缩与多程腔压缩在原理上是类似的，WANG Siyang等利用四组八片CaF2薄片将515 nm脉冲压缩到了40 fs［8］。激光成丝自压缩是一种复杂的脉冲压缩方法，主要利用自聚焦、电离诱导的散焦、自相位调制以及自陡峭等非线性效应的联合作用。KRETSCHMAR等利用激光在氩气中的成丝现象将780 nm脉冲压缩到了5.3 fs［9］。充气空芯光纤是一种成熟的后压缩方法，压缩后的光脉冲具有极高的光束质量，其已经广泛运用在800 nm以及中红外等波段，例如ANDERSON A等利用充氖气的空芯光纤将800 nm的脉冲压缩到了5.7 fs［10］；WANG Pengfei等利用充氪气的空芯光纤将4 μm的脉冲压缩到了21.5 fs等［11］。对于由1 030 nm倍频得到的515 nm脉冲，充气空芯光纤依然适用。例如DESCAMPS D等报道了利用倍频的515 nm脉冲的压缩结果，但是他们最终只得到了14.8 fs的压缩脉宽，并没有压缩到两个周期以内［12］。如何利用充气空芯光纤将倍频得到的515 nm的脉冲压缩到近单周期，依然是一个研究重点。

本文理论研究了对515 nm脉冲基于充气空芯光纤的后压缩。初始输入脉冲参考Light Conversion公司的掺镱激光器的输出，通过建立理论模型，优化了空芯光纤参数（纤径、长度、气体类型、气压等），最终获得了近单周期的脉宽，压缩倍数达到100左右，并在此基础上证明了多级压缩在后压缩技术中的有效性。本工作对后压缩方法获得高平均功率、高重复频率、少周期、高光束质量的飞秒激光具有重要的指导意义，推动先进阿秒光源和阿秒科学研究快速发展。

1 理论模型

脉冲在空芯光纤的传输过程中同时受到色散效应以及非线性效应的影响。色散效应与非线性效应的联合作用，描述了脉冲在空芯光纤中传输时的波形变化情况。从基本的麦克斯韦方程组出发，可以推导得到脉冲在空芯光纤中传输时满足的时域广义非线性薛定谔方程［13］

式中，z是脉冲在光纤中的传输距离，T=t-z/vg=t-β1z是随脉冲以群速度vg移动的参考系中的时间量度，A（z，t）是脉冲时域振幅，αloss是介质的损耗系数［14］

式中，a为纤芯半径，κ为空芯光纤外部（熔融石英）和内部（气体）介质的折射率之比。βk=(dkβ/dωk)|ω=ω0代表介质的k阶色散，γ=n2ω0/cAeff代表介质的非线性系数，其中n2=(p/bar)·C为非线性折射率，根据气体类型的不同，C为不同的数值。Aeff=0.48πa2为纤芯的有效面积。式（1）的等式左侧描述了脉冲传输过程中的色散效应，包括损耗（第二项）与各阶色散（第三项）。而式（1）的等式右侧则描述了脉冲传输中的非线性效应，包括自相位调制（第一项）与自陡峭效应（第二项）。

式（1）是一个非线性偏微分方程，在一般情况下无法获得有效的解析解，只能使用数值方法求解。常用的数值方法包括频域有限差分法，即将式（1）傅里叶变换到频域得到

式中，ϵ0为真空介电常数，R为理想气体常数，Nα为阿伏伽德罗常数，α为惰性气体的分子极化率

式中，Tref和pref分别为标准条件下的温度与压强，nref为对应状态下的折射率。由此根据β=nω/c可以求得脉冲在空芯光纤中的传播常数。

2 计算结果与讨论

仿真中的光源参考Light Conversion公司的PH2-2mJ-SP激光器，其中心波长为1 030 nm，重复频率为10 kHz，脉冲能量为2 mJ，考虑50%的倍频转换效率，得到中心波长为515 nm，脉冲能量为1 mJ的输入脉冲，脉宽为250 fs，峰值功率为4×109W。为了在空芯光纤中以最小的损耗实现受控的光谱展宽，一个重要的条件是脉冲的峰值强度应小于惰性气体的光电离阈值强度Ith，即P≤Ith·Aef［f15］。惰性气体的Ith在1014W/cm2量级［16］，由此可以得到纤芯半径为a≥50 μm，在此基础上可以忽略电离对脉冲频谱展宽过程中的影响。此外，由于脉冲在空芯光纤中传播时会受到波导结构的限制，始终保持固定的模式传播，因此可以忽略脉冲传输过程中空间效应的影响。本文使用氩气与氪气进行模拟，在标准条件下氩气与氪气的n2分别为10-23m2/W，2.8×10-23m2/W［17-18］。令模拟过程中二者对应的最大压强分别不超过10 bar、3.5 bar（1 bar=100 kPa），即相当于二者的最大非线性折射率n2相同，为10-22m2/W。图1（a）、（b）分别显示了根据式（4）计算得到的充气空芯光纤的传输特性曲线，纵坐标为气体的群速度色散（Group Velocity Dispersion， GVD）。对于氩气，压强划分为 1、2、4、6、8、10 bar，氪气为 1、1.5、2、2.5、3、3.5 bar。计算表明充气空芯光纤的 GVD始终大于0，是正色散材料。

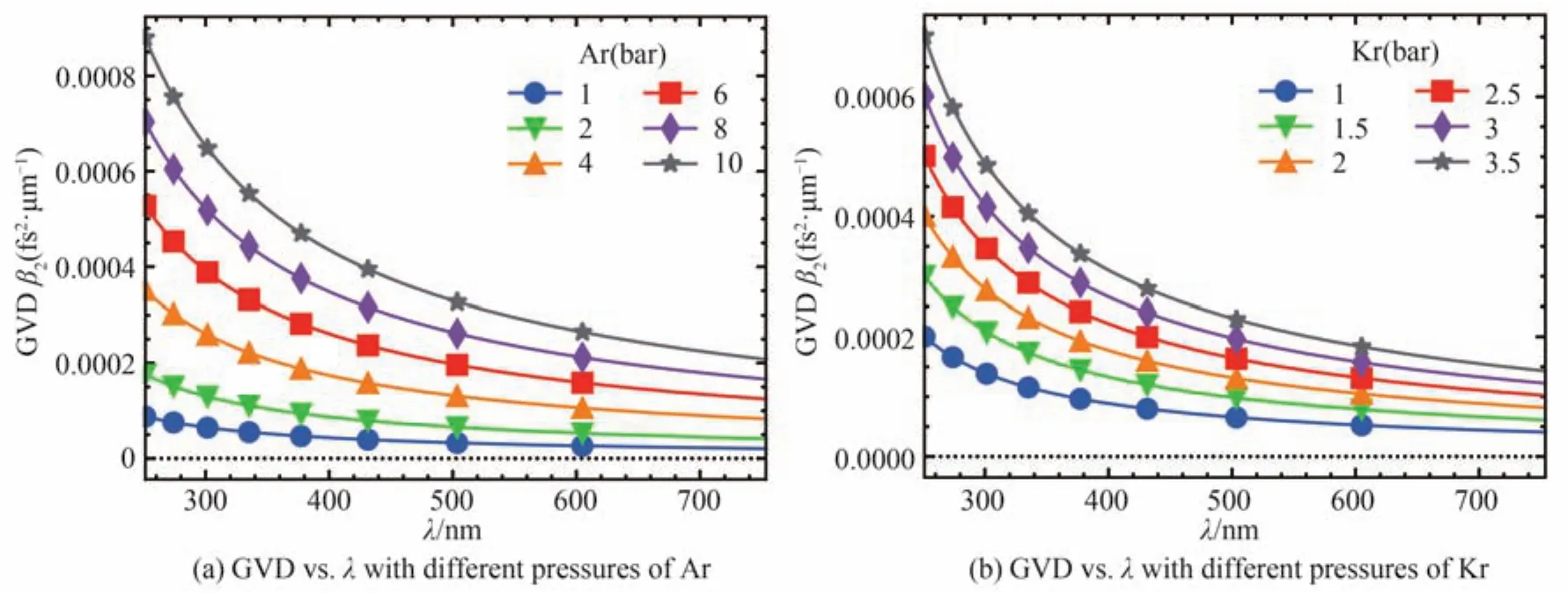
图1 不同压强/波长对GVD的影响Fig.1 The effects of different pressures/wavelengths on GVD

脉冲在空芯光纤中传输时因为损耗系数αloss的影响，其能量会以e-αlossL随着传输距离的增加而逐渐衰减。此外根据式（2）可知，αloss与纤芯半径a的三次方成反比，所以脉冲的传输效率也会受到a的影响。图2（a）显示了以氩气为例，在标准条件下（1 bar）脉冲在空芯光纤中的传输效率η与纤芯半径a和传输距离L之间的关系。图中白线代表η为50%的位置。白线的右侧代表η大于50%，而白线的左侧代表η小于50%。理论上传输效率η还会根据式（2）与式（5）中的惰性气体的折射率与压强的关系从而受到压强的影响。但是计算可得压强对气体折射率的影响在千分位上，其对于传输效率η的影响可忽略不计，所以图2（a）对于前述1～10 bar的压强划分都是适用的。对于氪气同理，氪气与氩气的折射率在标准条件下分别为1.000 3和1.000 4（515 nm处），对于传输效率的影响同样可忽略不计，所以图2（a）对于氪气也同样适用。

图2 纤芯半径a的选取原则Fig.2 Selection principle of fiber core radius a

另外，在忽略色散与自陡峭效应的影响时，可以推导得到输出脉冲的谱宽与输入脉冲的谱宽之比展宽因子F的表达式为［19］

φmax=γPLeff是最大非线性相移，其中Leff=[1-exp(-αlossL)]/αloss为空芯光纤的有效长度。由式（5）可知，展宽因子F与纤芯半径a，传输距离L以及气体压强p的取值有关。在图2（b）、（c）中分别使用氩气与氪气，计算得到了在标准条件下（1 bar）F与a和L之间的关系。对于压强，由于展宽因子F中根式下第二项要远大于1，所以在近似条件下。这样F就与压强成正比，因此对大于1 bar的压强，只需对图2（b）、（c）乘以相同的比例即可。另外根据F≈0.88φmax可以发现，不同气体中的展宽因子差别只在于各自的非线性折射率n2不同，所以图2（b）、（c）中的变化趋势是一致的，差别仅在于氪气的F在相同条件下数值更大。根据傅里叶变换极限脉冲的时间带宽积理论，要想获得具有更短时域脉宽的激光脉冲，脉冲的频谱必须被扩展到足够宽，一般为一个倍频程。对于中心波长为515 nm的脉冲，倍频程的范围大致为350～700 nm，换算到角频率域的范围为2.7×1015rad/s。而其初始谱宽，因此认为展宽因子大于400都是可行的，此时可以计算得到在最大非线性折射率n2下的传输长度L应大于2.35 m。这样由图2综合考虑，最终确认纤芯半径a为125 μm。

由于式（6）中只考虑了自相位调制，并且式（6）只是一个估算公式，所以需要通过进一步的模拟来验证合适的压强与传输距离，使得脉冲的频谱可以在充气空心光纤中展宽达到倍频程。图3显示了在氩气中使用不同组合得到的脉冲展宽结果，其中以初始脉冲进行归一化。由图3（a）可以发现，在10 bar，2.5 m；8 bar，3 m；6 bar，4 m的时候，脉冲的频谱都可以达到倍频程，并且三者的谱形是类似的，此时计算得到三种组合的展宽因子F与传输效率η分别为423，0.86；400，0.84；389，0.79。这样的频谱都支持将脉冲的时域脉宽压缩至近单周期，考虑到10 bar，2.5 m组合下的F与η均为最大值，所以选择10 bar，2.5 m的组合对脉冲进行压缩。

图3 在Ar中不同压强与长度组合的展宽比较Fig.3 Comparison of broadening for different combinations of pressure and length in Ar

上述讨论是针对氩气的，对于氪气同理。图 4（a）、（b）显示了在 3.5 bar，2.5 m；3 bar，3 m；2.5 bar，3.5 m三种组合下脉冲的展宽情况，对应的F与η分别为414，0.86；420，0.84；403，0.81。因为在氪气与氩气分别取到各自最大压强的时候二者的最大非线性折射率n2是相同的，都为10-22m2/W，所以在忽略色散的情况下，二者在最大压强下经过相同的传输距离后频谱的展宽程度与谱形应该相同。但可以发现对于图4（a）中3.5 bar，2.5 m的频谱相较于图3（a）中10 bar，2.5 m的频谱略有不同，这种差别主要来自于二者的GVD不同，这也导致了图4（b）中时域的展宽范围整体要略小于图3（b）的范围。考虑F与η，并且为了与氩气的情况进行对比，同样对于氪气选择3.5 bar，2.5 m的组合。

图4 在Kr中不同压强与长度组合的展宽比较Fig.4 Comparison of broadening for different combinations of pressure and length in Kr

经过上述讨论，最终确定了脉冲分别在氩气与氪气中进行频谱展宽的合适参数。图5（a）、（b）与（c）、（d）分别显示了脉冲在氩气与氪气中传输时频谱与时域随传输距离的演化图。其中图5（a）、（c）为了方便观察，对纵坐标进行了截取。观察图5（a）、（c），由于受到自相位调制随传输距离增大而变大的影响，可以发现脉冲的频谱从中央区域发生了分裂现象，并且由于自陡峭效应的存在，导致分裂的频谱左右两侧是不对称的。此外随着传输距离的增大，GVD的影响也会逐渐增大，导致脉冲频谱的多峰结构发生明显变化，中央区域的振荡峰趋于平缓。此外GVD会产生线性啁啾，而自相位调制则会产生非线性啁啾。两种频率啁啾混合，会使得脉冲的不同部分以不同的速度传输，特别在正色散区（β2＞0），脉冲前沿的低频光传播速度更快，并会与脉冲后沿的高频光发生干涉，而相反的情况发生在脉冲的后沿。这会在时域产生振荡结构并在频谱边带附近生成新的频率分量，从而导致对脉冲进行整型［20-21］。因此会表现为随着传输距离的增大脉冲由高斯型逐渐转变为矩型，图3（b）与图4（b）对这种现象有更清晰的展示，而矩型左右不对称的原因是自陡峭效应导致的频谱的不对称性。

图5 脉冲随空芯光纤长度的演化图Fig.5 Evolution of the pulse with the length of the hollow core fiber

在上述的计算中已经得到了脉冲频谱分别在氩气与氪气中的展宽结果，其与展宽前的频谱对比分别如图6（a）、（c）所示，图中红色虚线为色散补偿后的频谱相位，相位利用复振幅的虚部与实部的反正切求得。利用η=(∑ωA2ω)/E0计算了在氩气与氪气中展宽后的脉冲能量传输率，均为0.86，与前述中利用公式计算得到的结果吻合。展宽后的频谱能够支持的傅里叶变换极限（Fourier Transform Limited， FTL）脉冲如图6（b）、（d）中阴影部分所示，其脉宽分别为2.32 fs与2.13 fs。之后对脉冲频谱进行色散补偿，即可得到压缩后的脉冲，模拟中的色散补偿是通过对频谱的相位添加负的GDD完成的。在实际的实验中，宽带频谱补偿可以使用啁啾镜，例如UltraFast Innovation公司的PC1332啁啾镜可以在400～1 000 nm的范围内对GDD进行补偿。图6（b）蓝线显示了在氩气中得到的压缩结果，当补偿的二阶色散（Group Delay Dispersion，GDD）为-769 fs2时，可以得到最短脉宽为2.91 fs的脉冲，红色虚线为色散补偿后的时域相位。相较于阴影部分的FTL脉冲，最终压缩得到的脉冲在底部还残留有一些小振荡峰。这些振荡峰的出现来源于脉冲传输过程中获得的高阶色散，它们会使得压缩得到的主脉冲的峰值功率下降。图6（d）是在氪气中得到的压缩结果，当补偿的GDD为-580 fs2，可以得到最短脉宽为2.62 fs的脉冲，其中的红色虚线同样为色散补偿后的时域相位。可以看到，对于氩气与氪气，在相同的最大非线性折射率与传输距离下二者的压缩效果是类似的，均成功将脉冲压缩至两个周期以内（ 周期为1.72 fs）。

图6 脉冲的频谱展宽与时域压缩Fig.6 Pulse spectrum broadening and time domain compression

虽然图6显示的结果证明使用充有惰性气体的空心光芯可以将250 fs的脉冲压缩到近单周期，但从图6（b）、（d）可以看出，这时压缩得到的脉冲还残留有许多振荡结构，这是因为在频谱展宽的过程中引入了过多的高阶色散，这些高阶色散很难被补偿。因此，对于初始脉宽达250 fs的脉冲，可以使用多级压缩的方式进行压缩，如图7（a）所示，倍频得到的515 nm脉冲先经过第一级的多程腔进行压缩，将压缩后的脉冲再通过第二级的充气空芯光纤进行压缩，这样可以有效解决高阶色散过多的问题。第一级压缩参考HARITON V等的工作，他们在实验中利用多程腔成功将倍频得到的515 nm，250 fs的脉冲压缩至38 fs［7］。在第二级使用充有0.2 bar氩气、长度为1 m的空芯光纤进行压缩。仍然保证输入脉冲的能量为1 mJ，纤芯半径为125 μm。图7（b）是脉冲频谱展宽前后的对比图。在使用-20 fs2的GDD补偿后，可以得到图7（c），此时脉冲的波形趋于完美，脉宽为2.08 fs，其中阴影区域为展宽后的频谱支持的FTL脉冲，脉宽为2.04 fs。同样使用氪气可以对脉冲实现相似的压缩，图7（d）、（e）显示了压强为0.1 bar，长度为0.8 m的压缩结果。最终压缩得到的脉宽为2.03 fs，此时的FTL脉宽为2 fs。

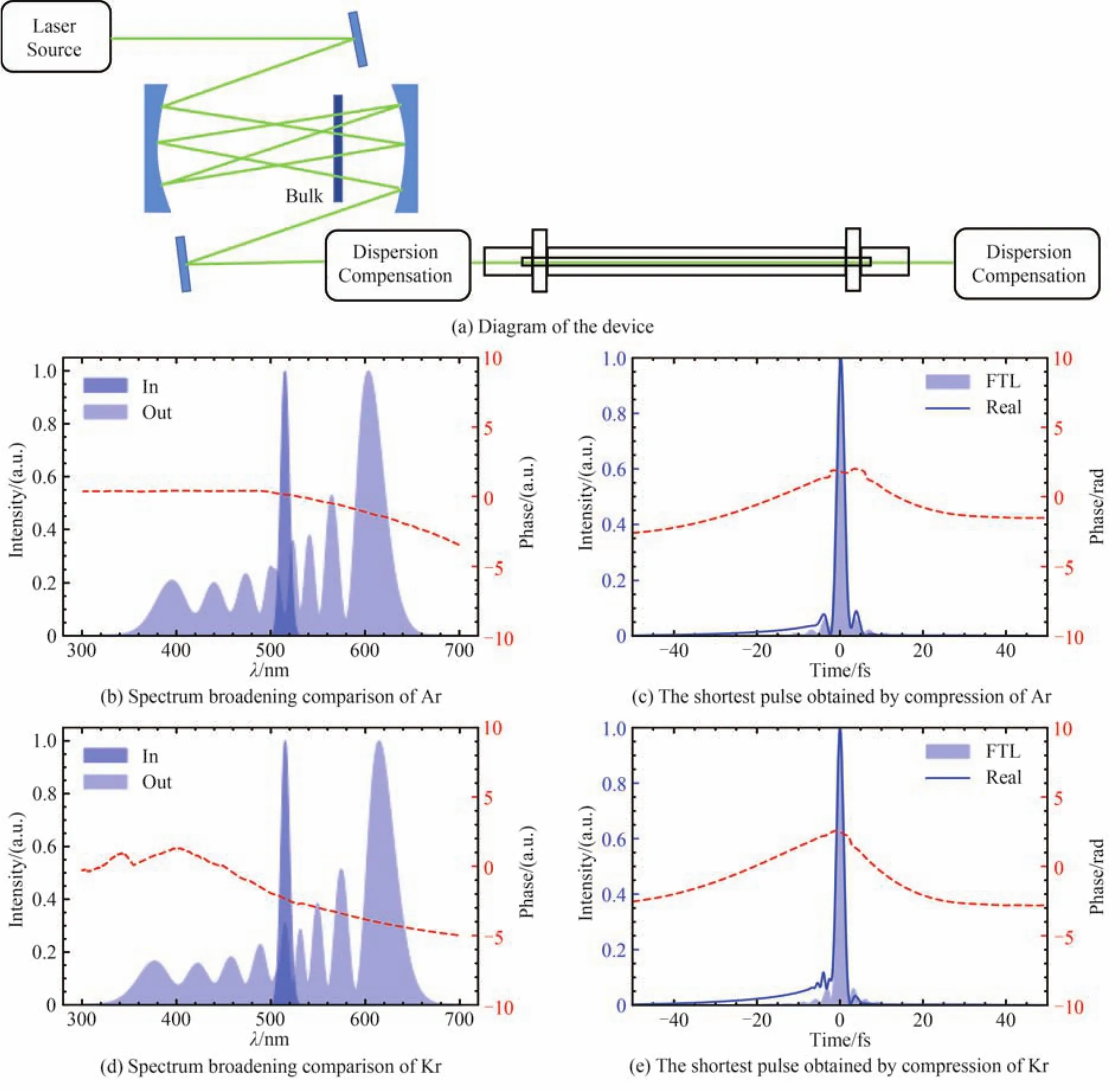
图7 使用第一级压缩得到的38 fs脉冲进行第二级压缩Fig.7 Second stage compression using 38 fs pulse from first stage compression

3 结论

近单周期的短波长脉冲在孤立极紫外阿秒脉冲产生等领域有重要的意义。本文理论模拟了基于充气空芯光纤的后压缩过程，将掺镱激光器倍频脉冲的脉宽压缩至近单周期。利用理论模拟优化了空芯光纤参数，证明经过色散补偿后可以在充有氩气或氪气的空芯光纤中实现100的压缩比，最终获得小于两个周期的脉冲，与DESCAMPS D等［12］利用充气空芯光纤在515 nm处压缩得到的15 fs的实验结果相比从理论上论证了获得更短压缩脉冲的可能性。这样短脉宽、短波长的脉冲可以极大提高由高次谐波产生阿秒光源的效率。但是使用充气空芯光纤直接将250 fs脉冲压缩至近单周期，会产生很多难以补偿的高阶色散，这会使脉冲的对比度下降，造成能量损失。这时可以采用多级压缩的方式，先对250 fs的脉冲使用多程腔压缩，在第二级再使用充气空芯光纤压缩，这样可以有效减少高阶色散的产生，实现对比度更高的脉冲输出。另外模拟中在空芯光纤内使用了均匀的气压，而在实验中可以采用梯度气压避免光纤入口处的有害非线性效应［22］，而且色散补偿中单一啁啾镜的有限补偿带宽也是限制实验中获得少周期脉冲的重要因素。本文的理论研究工作将对基于掺镱高功率亚皮秒激光器获得少周期光脉冲提供重要的理论指导，这对推动高性能阿秒光源研制和阿秒科学研究具有重要意义。