抗弯刚度对斜拉索-黏滞阻尼器系统风致振动影响的研究
2023-07-12宋福春付聿旻
宋福春,付聿旻
(沈阳建筑大学交通与测绘工程学院,辽宁 沈阳 110168)
斜拉索作为斜拉桥主要承重构件,具有质量轻、柔度大、阻尼低等特点,极易在风荷载的作用下产生各种类型的振动从而引起结构破坏。为抑制拉索的大幅振动,在拉索锚固端附近安装阻尼器是目前广泛使用的减振方法之一。黏滞阻尼器作为常用的阻尼器之一,以其参数稳定、安装方便、减振效果好等优点,适合作为斜拉索永久抑振措施。为了得到黏滞阻尼器抑振性能的数据,学者们通过大量数值理论研究了斜拉索-黏滞阻尼器系统的运动方程及其求解。
B.M.Pacheno[1],J.A.Main[2],S.Krenk[3-4]等学者通过不同的计算方法,得到了黏滞阻尼器的理论数值,但这些研究都是针对紧索情况,忽略了斜拉索的初始垂度以及抗弯刚度。部分学者研究了拉索中垂度和弯曲刚度对斜拉索阻尼的影响:H.Tabatabai等[5]认为对于大多数斜拉索而言,拉索垂度的影响不显著,而拉索抗弯刚度会对拉索阻尼比产生显著影响;S.Krenk等[6]研究了安装在下垂索末端附近黏滞阻尼器的最佳调谐和模态阻尼效果,计算低阶模态的完整解,得到了相当精确的解析近似值,并推广了张紧拉索的计算结果;J.A.Main等[7]使用动态刚度的方法,建立了带有黏滞阻尼器受拉梁的自由振动精确解析解;Y.Fujino等[8]对考虑抗弯刚度的下垂索进行了综合分析,对于黏滞阻尼器,影响参数被明确纳入模态阻尼公式中的修正因子,说明了垂度和抗弯刚度对斜拉索模态阻尼的影响;周强等[9]对不同边界条件、不同线性黏滞阻尼器参数下斜拉索抗弯刚度对系统一阶模态阻尼比的影响进行了研究,结果表明,考虑斜拉索抗弯刚度以及垂度会影响斜拉索模态阻尼比以及安装的黏滞阻尼器最佳阻尼系数的取值,但斜拉索由于抗弯刚度较小,通常视为完全柔性,对忽略斜拉索抗弯刚度所带来影响的研究还不够深入。
综上所述,笔者基于斜拉索-黏滞阻尼器系统振动规律,以沈阳市昆山西路斜拉桥为实际工程背景,采用有限元分析方法,使用不同单元模拟斜拉索,研究风荷载作用情况下,是否考虑抗弯刚度对斜拉索以及斜拉索-黏滞阻尼器系统的影响。研究表明,抗弯刚度在斜拉索以及斜拉索-黏滞阻尼器系统的动力分析中非常重要,不可忽略。
1 斜拉索-黏滞阻尼器系统有限元建模
以沈阳市内昆山西路斜拉桥为例,该桥为单塔斜拉桥,桥跨长度为275 m,桥宽31 m,左跨长155 m,选取左跨上的三根斜拉索,位置如图1(b)中标线所示,从短到长依次编号为1、2、3号。三根斜拉索各项数据如表1所示。

表1 斜拉索编号与力学参数Table 1 The cable number and mechanical parameters
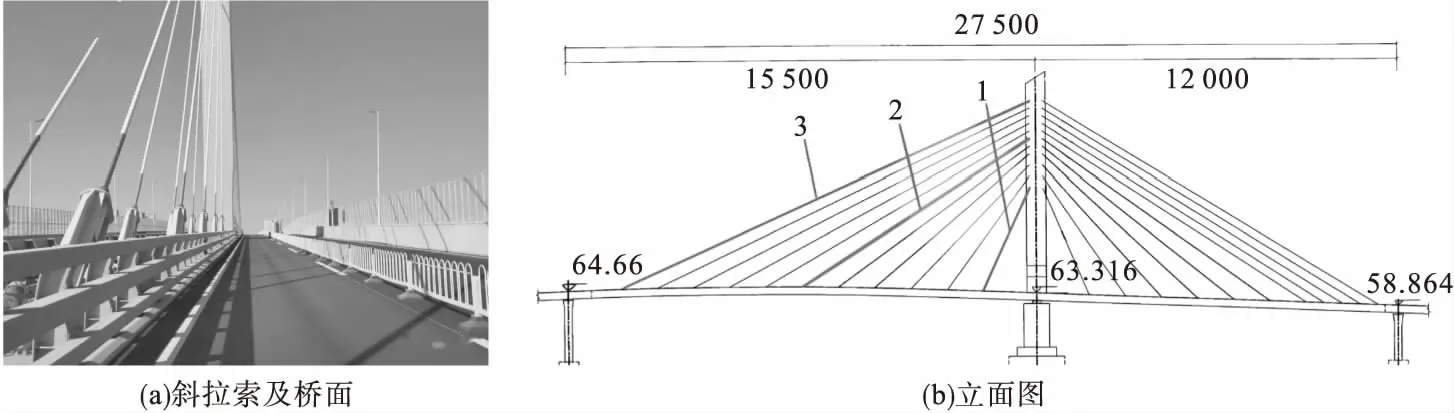
图1 昆山西路斜拉桥Fig.1 The cable stayed bridge on Kunshan west road
计算时使用ANSYS软件,模型示意图如图2所示。
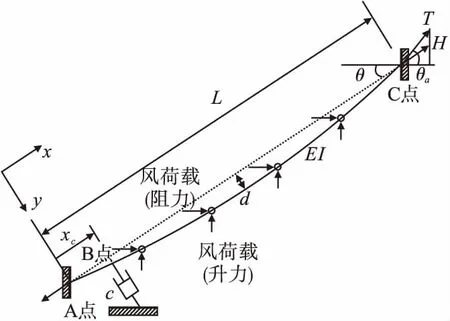
图2 斜拉索-黏滞阻尼器系统示意图Fig.2 The schematic diagram of cable viscous damper system
以斜拉索弦线为x轴,梁端锚固点到塔端锚固点方向为x轴正方向;以弦线垂线为y轴,斜拉索下垂方向为y轴正方向。
斜拉索在每米自重(线密度)M作用下线型为悬链线,弦长为L,抗弯刚度为EI。根据张紧索预应力H求得斜拉索的实际预应力T,以及其实际与水平方向夹角θa。
通过二分法,设置多次迭代计算,求得斜拉索索内各微段水平力的大小。通过该水平力的值计算成桥状态下斜拉索的曲线方程,建立分段模型。根据斜拉索无应力长度以及受荷时的长度,得到初应变大小,通过设置斜拉索材料初应变的方式施加预应力。模型在梁端锚固点A以及塔端锚固点C均约束所有自由度,每一段分别施加不同的风荷载(见图2中箭头)。
在ANSYS软件中,通常使用只承受拉压的杆单元link180来模拟斜拉索。而梁单元beam189除了承受拉压以外,还可以承受弯矩。分别使用link180单元和beam189单元建模计算,将使用link180单元建模的模型称为杆单元模型,使用beam189单元建模的模型称为梁单元模型。
黏滞阻尼器使用combin14单元模拟,在与A点距离为xc处的B点建立阻尼器单元,该单元一端与斜拉索相连,另一端固结,与斜拉索弦线方向垂直,阻尼系数值为c。
采用上述方法建立有限元模型,并与试验结果进行对比。斜拉索试验的索采用7φ5钢绞线,数据如下:斜拉索长13.6 m,倾斜角度为57.7°,线密度为1.203 1 kg/m,横截面积为0.001 237 m2,预应力分别设置为50 kN和120 kN。钢索一端固定,另一端用千斤顶张拉。在索上不同位置安装加速度传感器采集加速度信号,使用频率域的峰值法得到固有频率[10]。
实测数据与有限元模态分析计算值对比如表2所示。
由表可知,计算结果误差较小,使用该方法计算斜拉索模态频率是可行的。计算得到表1中1、2、3号三根斜拉索第一阶模态频率分别为2.933 Hz、1.314 Hz、0.787 Hz。
2 风荷载
2.1 风速时程
根据大量风的实测数据可以看出,在风的顺风向时程曲线中包含两个部分:一种是长周期部分,其周期值常在10 min以上;另一种是短周期部分,其周期通常只有几秒左右。因此,常把风分为平均风和脉动风加以分析:
(1)
平均风沿高度方向成指数函数变化,使用规范规定的标准风压值转换得到。脉动风速时程通常使用自回归方法模拟,该方法模拟速度快计算量小且具有较高精度[11-12]。依据自回归方法编制程序,水平方向脉动风速使用Simiu谱,竖直方向使用Panofsky谱。
计算得到各坐标点处脉动风速时程后,使用快速傅里叶变换(FFT)得到随机脉动风速时程的功率谱,风速时程计算结果与功率谱对比如图3所示。由图可知,模拟谱与目标谱吻合较好,说明了程序计算的脉动风速时程正确。

图3 水平脉动风速时程计算结果Fig.3 The time history calculation results of horizontal fluctuating wind speed
2.2 风荷载时程
斜拉索受到风荷载作用时,其受力可以分为平均风速引起的静风荷载,脉动风引起的抖振力和流固耦合引起的自激力。拉索直径很小,自激力量小,拉索的自激力荷载对整个结构的振动影响不大,故忽略自激力的影响[13]。
单位长度斜拉索所受的静风荷载:
(2)
(3)
式中:Ls,Ds分别为静风荷载的升力和阻力;ρ为空气密度;U为任意高度处的平均风速;B为斜拉索直径;CL(γ),CD(γ)分别为风攻角等于γ时的升力系数和阻力系数,风方向为顺桥向时阻力系数取为1[14]。
根据Davenport的准定常假定,单位长度拉索受到的抖振力[15]:
(4)
(5)
式中:Lb(t)、Db(t)分别为抖振力的升力和阻力;u(t)、w(t)分别为水平方向、竖直方向脉动风速时程;CL′(γ)、CD′(γ)分别为升力系数、阻力系数的一阶导数。
将上述两个部分相加得到单位长度斜拉索受到的风荷载大小,输入斜拉桥所处位置环境参数及各点坐标后,可以得到各点单位长度荷载时程数据(见图4)。
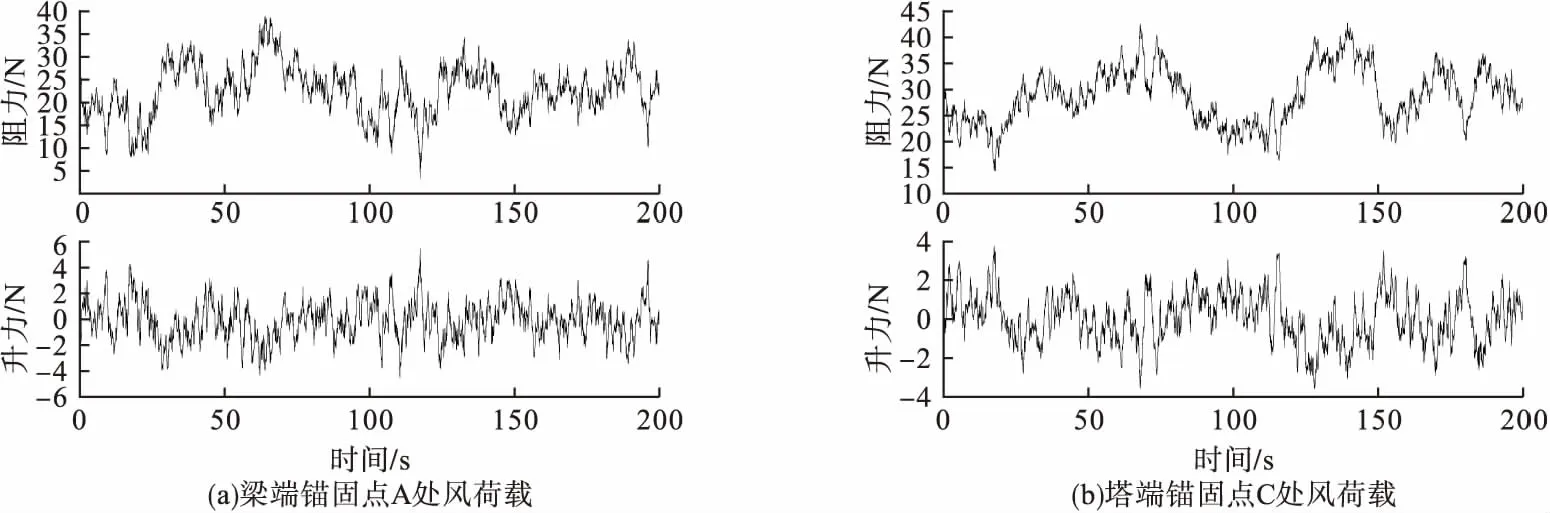
图4 单位长度斜拉索阻力、升力时程图Fig.4 The drag force and lift force per unit length of stay cable
3 斜拉索-黏滞阻尼器系统数值模型
Y.Fujino等[8]研究得到了斜拉索垂度以及抗弯刚度两个变量对斜拉索模态阻尼比和无量纲阻尼器参数的修正系数。在斜拉索计算中,n为模态阶数,ξn为斜拉索第n阶模态阻尼比,Rsn为垂度引起的模态阻尼比修正系数,Rf为考虑抗弯刚度时模态阻尼比的修正系数。在考虑斜拉索垂度的情况下,不考虑抗弯刚度的斜拉索最大模态阻尼比为
夜渐渐地深了,凉棚里也安静了下来,亲友们都找到了躺处,姗姗离去;最后只剩下三五个至亲零零散散地坐在外面打瞌睡,但没有看见高木,他大概回麦村去了。黄方永玩累了,像煨灶猫一样缩在母亲的怀里。小家伙浑身是汗,头发湿搭搭的。桃花轻轻地抱起他,去了里屋,把他放在自己的小床上。小家伙着床时呜咿了几声,在桃花的轻拍下,终于甜甜地入睡了。
(6)
考虑抗弯刚度时斜拉索最大模态阻尼比为
(7)
在黏滞阻尼器参数的计算中,ηn为无量纲阻尼器参数,ηsn为斜拉索初始垂度对无量纲阻尼器参数的修正系数,ηf为斜拉索抗弯刚度对无量纲阻尼器参数的修正系数。
(8)
(9)
(10)

由此可以得到式(6)中系统模态阻尼比最大值在满足式(11)条件时取得。
(11)
即不考虑抗弯刚度时,第n阶模态对应的最佳阻尼系数:
(12)
式(7)中系统模态阻尼比最大值在满足式(13)条件时取得。
(13)
(14)
4 计算结果对比
4.1 抗弯刚度对斜拉索初始垂度的影响
斜拉索初始垂度包括两部分:第一部分为建立斜拉素模型时各点的垂度;第二部分为有限元进行静力计算的垂度。各关键点这两个部分的垂度大小如表3所示。

表3 斜拉索各点初始垂度对比Table 3 The comparison of sag values at selected points for different stay cables
由表3可知,理论公式的计算结果包含了斜拉索上各点初始垂度大小的绝大部分。在有限元静力计算中,使用梁单元计算时,由于抗弯刚度的影响,静力计算结果大于使用杆单元的计算结果,且斜拉索越长,使用不同单元计算得到的差值就越大。
4.2 抗弯刚度对斜拉索风致振动的影响
求解器选为瞬态分析,通过载荷步的方式施加风荷载,由于斜拉索存在较大的几何非线性,初始状态需要通过几个荷载步逐步添加。分别使用杆单元模型以及梁单元模型计算斜拉索在无阻尼器情况下受到风荷载作用时的振动情况。对于同一斜拉索,使用不同单元模型计算时采用的风荷载时程相同,其中2号斜拉索中点处的位移时程如图5所示。
由图可知,梁单元模型的位移时程曲线最大值在5 mm左右,振幅在4.5 mm左右;杆单元模型的位移时程曲线最大值在10 mm左右,振幅在9 mm左右。使用不同单元模型计算得到的中点处位移时程有较大不同,位移时程在考虑抗弯刚度后降低为不考虑抗弯刚度时的1/2左右。
4.3 抗弯刚度对斜拉索-黏滞阻尼器系统风致振动的影响
采用式(12)和式(14)计算三根斜拉索上黏滞阻尼器在一阶模态,即n=1时对应的最佳阻尼系数值,计算中阻尼器的安装位置比xc/L均取为2%,一阶模态频率按表2中的计算结果取值,结果如表4所示。分别用梁单元模型和杆单元模型依次计算阻尼系数为copt1和copt2的两个不同参数黏滞阻尼器的抑振效果。对于同一根斜拉索,在使用不同的单元、输入不同的阻尼器参数时,使用的风荷载均相同。
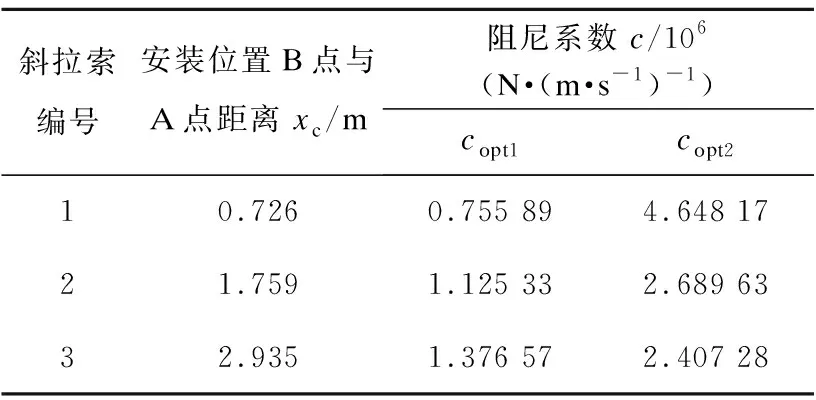
表4 不同斜拉索最佳阻尼系数值Table 4 The optimum damping coefficients of different stay cables
使用杆单元建模进行计算时,斜拉索上的各点的位移均方根(RMS)如表5所示。1、2、3号斜拉索安装阻尼系数为copt1的阻尼器后,斜拉索上的1/4、1/2、3/4三点的RMS值均降至最低,明显优于安装阻尼系数为copt2的黏滞阻尼器的情况。
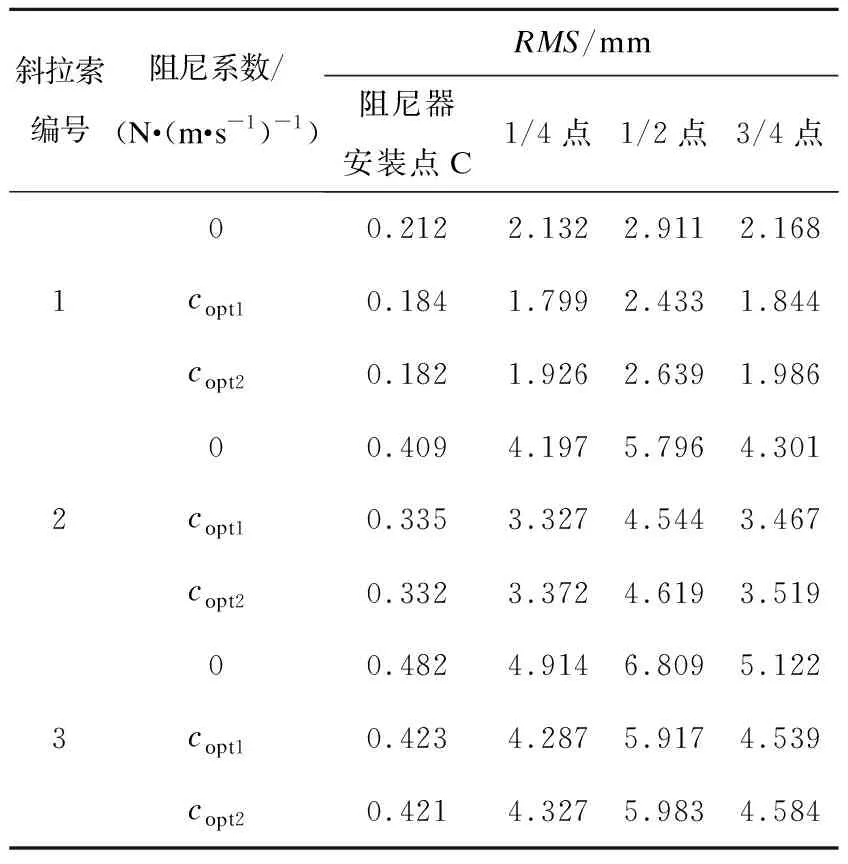
表5 杆单元模拟斜拉索各点RMS值对比Table 5 The comparison of RMS values at selected points in cable element simulation for stay cable
使用梁单元建模进行计算时,结果如表6所示。1、2、3号斜拉索在安装阻尼系数为copt2的阻尼器后,斜拉索上的1/4、1/2、3/4三点RMS值均降至最低。
由文献[16]研究可知,随着阻尼系数的增加,阻尼器抑振能力先增强后减弱。在使用杆单元建模进行计算时,黏滞阻尼器最佳阻尼系数值先于使用梁单元建模进行计算时出现,与理论公式的规律吻合。在1、2、3号斜拉索中,其对应的copt2值都远大于copt1值,特别是在较短的1号索中,copt2为copt1的6.15倍。如果使用杆单元建模进行计算,结果会指向一个较小的最优阻尼系数区间,导致出现较大的误差。而使用梁单元建模计算,则会指向更准确地阻尼系数区间,从而更精确的模拟风荷载作用下应该使用什么参数的阻尼器,无需在计算基础上较安全地选用更大阻尼系数的黏滞阻尼器。
将位移时程曲线转换为频率域中的位移功率谱密度(PSD)曲线,分析斜拉索-黏滞阻尼器系统在受到风荷载时的峰值响应大小。对比使用梁单元建模计算的3号斜拉索上中点以及阻尼器安装点C的响应谱大小如图6、7所示。
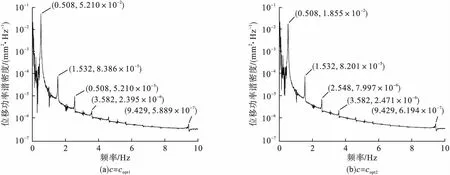
图6 3号斜拉索阻尼器安装点功率谱密度对比Fig.6 The comparison of damper installation position power spectrum density for No.3 stay cable
通常将0~3 Hz内的振动视为低频振动,3 Hz以上的振动视为高频振动[18]。在之前的计算中都只考虑了斜拉索的一阶模态对应的最佳阻尼系数值,而斜拉索在风荷载作用下表现为多模态结合的振动。由式(14)可知,对于斜拉索-黏滞阻尼器系统,计算中考虑的模态阶数越高,对应的最佳阻尼系数值越小,即copt1可以视为考虑抗弯刚度情况下斜拉索高阶模态对应的最佳阻尼系数值。图6中,阻尼系数为copt1时,前三个振动峰值较阻尼系数为copt2时高,而3.582 Hz之后的振动峰值较阻尼系数为copt2时低。对于图7所示的斜拉索中点处的功率谱密度,阻尼系数为copt2时,只有在0.508 Hz处的最大峰值较阻尼系数为copt1时低,其余峰值都不同程度的变大。考虑高阶模态设计的黏滞阻尼器对于斜拉索的高频振动抑制效果有提升,但不能有效地抑制最大的低频振动,由于1、2、3号斜拉索中的高频振动峰值较小,针对斜拉索1阶模态设计黏滞阻尼器就能较好地抑制斜拉索的风致振动。
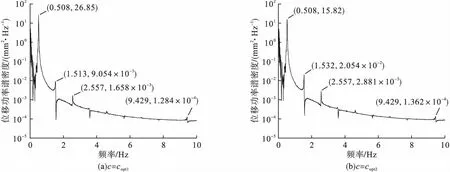
图7 3号斜拉索中点功率谱密度对比Fig.7 The comparison of mid point power spectrum density for No.3 stay cable
5 结 论
(1)对于长度在36~146 m间的1、2、3号斜拉索,考虑抗弯刚度时,有限元静力计算得到的初始垂度值更大,风致振动中的位移最大值和振幅大小为不考虑抗弯刚度时的2倍左右。
(2)对于安装于斜拉索上黏滞阻尼器,1、2、3号斜拉索中其对应的copt2分别是copt1的6.15倍、2.39倍和1.75倍;如果使用杆单元建模进行计算,会指示错误的阻尼系数区间,需使用能考虑抗弯刚度的梁单元建模进行斜拉索或者斜拉索-黏滞阻尼器系统的风致振动计算。
(3)设计黏滞阻尼器阻尼系数时,考虑高阶模态设计黏滞阻尼器能降低3 Hz以上的高频振动,但低于3 Hz的振动会变大,对斜拉索整体抑振不利;考虑第一阶模态设计黏滞阻尼器则能在风荷载作用时较好地抑制斜拉索振动。
