波流载荷作用下的下入安装立管横向动态特性*

2023-07-12孙巧雷刘语维夏乐冯定王鹏张红

石油机械 2023年6期

孙巧雷刘语维夏乐冯定王鹏张红

(1.长江大学机械工程学院 2.湖北省油气钻完井工程工具研究中心)

0 引言

采用立管下入安装水下设备是海上油气钻完井及生产作业的一种手段，立管的安全是保证水下设备顺利安装作业、确保下入设备上部载荷边界的基础[1-3]。受海洋环境载荷、海洋作业水深不断增加等因素影响，水下设备下入安装时立管的承载及动态变化复杂，基于此，笔者开展了波流载荷作用下的海洋立管下入安装横向动态特性研究。

对于海洋立管的横向动态分析主要包括微分方程法、纵横弯曲法、加权余量法、有限元法、能量法等，其中大部分的方法需首先建立立管的横向和纵向近似方程，再结合边界条件、网格划分后进行二次计算获得立管的位移、转角、应力等[4-5]。在相关研究中，周美珍等[6]基于建立的采油树下放过程钻杆的力学分析模型，进行下放不同阶段的最大横向位移分析；焦金刚等[7]通过建立深水送入管柱的物理模型，进行下沉管柱动态应力及送入管柱固有振动频率分析；刘康等[8]基于建立的送入管柱-导向环-导向绳的耦合动力学模型进行管柱应力分布、最大横向应力等分析；管志川等[9]通过建立送入管柱载荷计算模型，分析平台漂移、海流载荷等对管柱横向变形、应力等的影响。除上述研究外，相关学者围绕海上隔水管、测试管柱等进行了横向动态特性分析[10-12]，但鲜有针对立管下入安装水下设备时的横向动态特性分析。

基于此，笔者在对立管下入安装时波流载荷方程、立管横向承载方程的建立后，结合立管定解条件和模型求解方法，进行了实例井立管垂直至最大变形状态过程分析。并基于立管最大横向位移变化特点和底部位移动态变化规律，研究了波浪速度、管柱壁厚和作业水深对立管横向位移、底部弯矩等的影响特性。研究结果可为海洋立管下入安装设备时的安全作业控制提供基础，并为分析下入设备的上部边界提供条件。

1 海洋立管横向承载特性方程与求解

1.1 波流载荷方程

波浪力的计算目前主要基于Airy波理论和莫里森(Morsion)波浪力基本计算方法进行[13]。在考虑黏滞效应和附加质量效应基础上，作用于单位长度管柱的波浪力fw主要由水平黏滞力fI和拖曳力fD组成：

(1)

式中：ρw为海水密度，kg/m3；CD为拖曳力系数；D为管柱外径，m；u为水质点水平速度，m/s；CM为惯性力系数。

对于波浪水平速度和加速度可参照Airy波理论进行求解，拖曳力系数、惯性力系数根据作业海域海况及相关规范选取[14]。

对于海流载荷，一般根据稳定流动条件下阻力进行计算，单位长度立管上的海流力fc为[13]：

(2)

其中：

vc=u1(z/d)+u2(z/d)

(3)

式中：vc为距海底处的海流速度，m/s；u1为海面处潮流速度，m/s；u2为海面处海流速度，m/s；z为计算深度距离海底的深度，m；d为水深，m。

基于此，依据修正的Morsion方程，立管单元波流联合作用力Fx(z，t)为：

(4)

将水质点速度、波流速度等带入修正后的Morsion方程得到波流载荷计算公式为[14-15]：

(5)

式中：x为横向位移，m；λ为波长，m；H为波高，m；t为时间，s；T为波浪周期，s。

从式(5)可以看出，波流载荷是随时间变化的周期性载荷。为了便于计算，本文对波流载荷进行极值处理获得立管的最大横向位移。

1.2 立管横向承载方程

在风浪流等载荷作用下，立管的横向变形、转角、弯矩等变化明显，立管横向变形如图1所示。要研究立管的横向承载特性，首先需建立其横向承载方程。基于已有文献的研究成果[16]，在假设范围内，考虑波流载荷和管柱微元的惯性力以及内部流体的水平方向的惯性力(包括牵连惯性力、相对惯性力和科氏惯性力)，采用微元法建立了立管横向承载方程：

(6)

式中：E为立管材料的弹性模量，Pa；I为立管柱的截面惯性矩，m4；We为单位长度立管浮重，N/m；md为管柱单位长度内液体的质量，kg/m；mst为单位长度管柱的质量，kg/m；vi为管柱内液体的速度，m/s，T(z)为管柱轴向张力，N。

1.3 立管横向承载方程的定解条件

对于立管的上边界条件，立管的上端一般与钻井平台为铰接，考虑球铰刚度Ku，设平台漂移距离为S，则上端边界条件为：

(7)

本实例中，立管的下端与采油树为铰接，其下端边界条件为：

(8)

立管的上下边界需根据实际工况进行调整，其主要存在铰接、螺纹连接、顶部张紧等形式，具体需结合不同实例进行边界调整。

1.4 模型求解

为了对上述立管横向承载模型进行求解，本文采用目前应用较成熟、计算较稳定的有限差分法进行求解[3，16]。求解前需对立管在求解域内进行网格离散，离散后的网格域横坐标为时间域，纵坐标为管柱域，立管管柱节点按0～j进行编号，时间节点按照0～n进行编号，如图2a所示。此时离散后的求解方程为：

(9)

图2 立管网格划分图Fig.2 Grid division of the riser

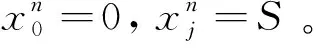
(10)

下边界为：

(11)

2 数值算例及求解分析

2.1 工程实例参数

本文以南海某作业井为例进行实例分析，该井作业水深约为1 500 m，管柱外径为476 mm，壁厚19 mm，弹性模量为210 GPa，材料密度为7 850 kg/m3，作业处海面处极端潮流速度为1.02 m/s，海面处极端海流速度为1.170 m/s，海水密度为1 030 kg/m3，波高为3.5 m，波浪周期为6.5 s，波长为65.9 m。根据相关规范选取拖曳力系数为1.2，惯性力系数为2，管柱顶部钩载设为1.1G(G为海水段钻井立管的重力)，管柱微元段长为h=1 m，时间步长为t=0.000 1 s。立管下部通过球铰与水下井口的防喷器连接。

2.2 计算结果

基于上述理论，通过Matlab编写程序对上述模型进行求解，编程过程除基本参数定义及矩阵生成外，还需对循环求解进行定义。图3为循环程序的部分源代码。

图3 循环子程序

此外Matlab求解过程中还需对方程的稳定性进行求解，该程序的稳定性条件采用矩阵的谱半径进行说明，在计算中通过调整时间步长使其满足稳定性条件。由于时间步和长度步较小，在数据分析时，可减小输出数据量，如通过命令行语句“B=x(3：25：end，3：200：end )”提取x(z，t)中行距为25h、列距200t的部分数据。基于上述参数及流程，获得平台无漂移下的立管由垂直形态到完全变形的形态如图4所示。

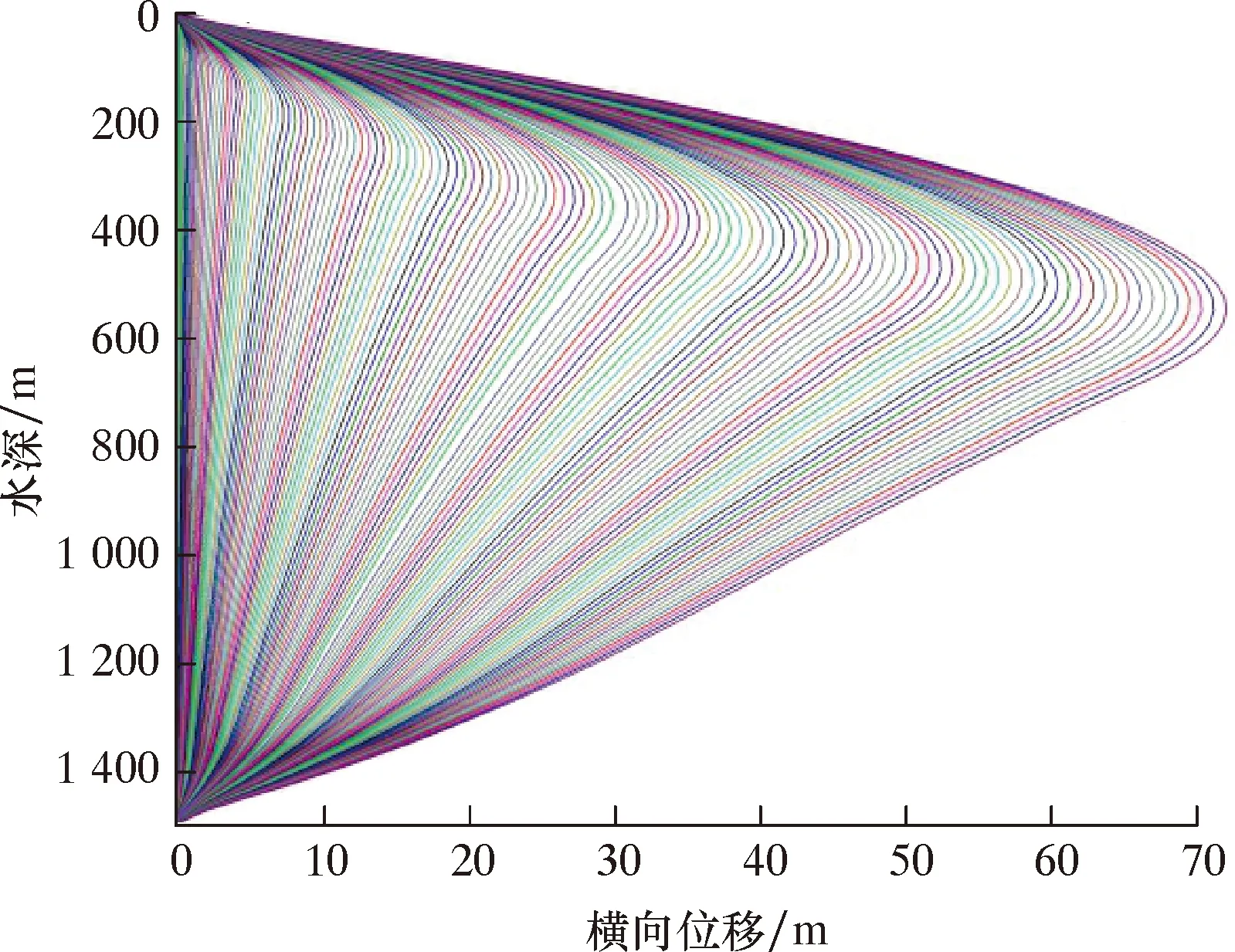
图4 立管变形过程图Fig.4 Deformation process of the riser

同时获取的关键时刻立管横向变形如图5所示。

图5 不同时间下的位移Fig.5 Displacement with time

由图4和图5可知，立管的最大横向位移由海平面逐渐扩展至水下500 m左右，整体上上部横向位移增大较快，下部减小较缓，直至泥线处为0。整体上最大位移的位置在水深的“”位置附近，这一现象与文献[17]的结论基本一致。同时通过详细数据分析发现，任意水深处立管横向位移随时间逐步增大，距离立管底部50 m内横向位移周期性波动增大，而10 m内波动幅度较为明显，且这一现象在平台产生漂移时更为明显。图6为距泥线1～6 m处的横向位移位移动态变化过程。后续研究基于这一实际及下部作业装备安全校核需求，对泥线处的弯矩进行进一步分析。

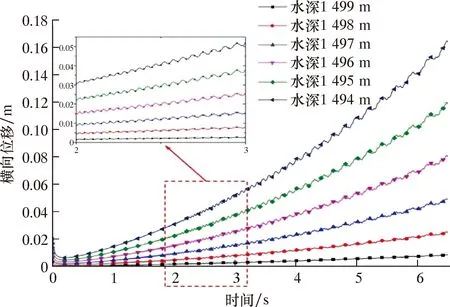
图6 立管底部横向位移动态变化Fig.6 Dynamic changes of lateral displacement at the riser bottom

2.3 时间步长误差分析

时间步长的大小除影响计算稳定性外，还会对数值计算的结果产生影响。在前述0.000 1 s时间步长研究基础上，进行了步长为0.000 08、0.000 20、0.000 50 s下的立管横向位移动态响应分析，对比了10 m漂移量不同时刻下的立管最大横向位移。对比发现，一个周期内，立管的最大横向位移位置均为508 m，最大位移分别为83.425 8、83.426 5、83.429 1、83.437 0 m，不同时刻时的最大位移量相对0.000 8 s时的误差如表1所示。不同时间步长计算的最大横向位移(t=6.5 s)误差均小于0.1%。同时对比主要时间下(0.5～6.0 s，时间间隔0.5 s)的位移误差，0.000 1 s计算步长位移变化过程最大误差为2.68%，而0.000 2、0.000 5均存在大于10%的数据。因此，选用时间步长为0.000 1 s的整体误差较小，满足无关性检验要求。

表1 不同时刻相对0.000 08 s横向位移误差值Table 1 Errors of lateral displacement at different time points relative to 0.000 08 s

3 不同工况因素分析

3.1 波浪速度影响分析

受海洋环境影响，波浪载荷在不同年月不同时间段变化明显。为了进一步研究波速对立管横向位移的影响，结合实例井所处海域波浪变化特点，进行了波浪速度分别为0.254、0.345、0.750、1.170 m/s下的立管横向动态特性分析，其结果如图7、图8所示，最大横向位移及水深位置如表2所示。由图7和表2相关结果可知：随着波浪速度的增大，立管的的横向位移增大，增大区域主要为海平面至1 400 m水深处；同时，在当前波浪速度范围内，立管最大横向位移与波浪速度近乎呈正比，且最大位移水深位置一定程度减小。

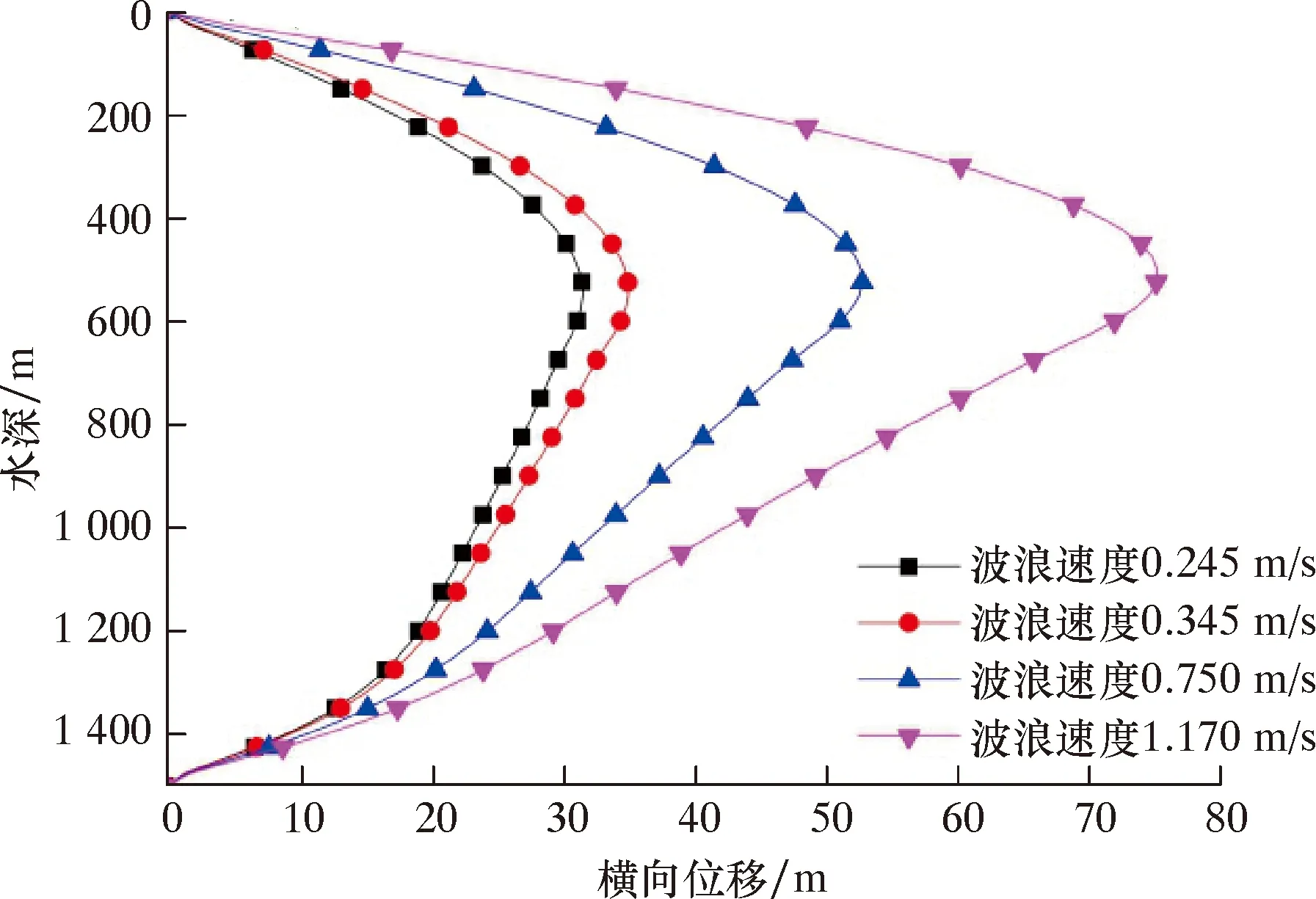
图7 不同波浪速度下的立管最大横向位移Fig.7 Lateral maximum displacement of the riser at different wave velocities

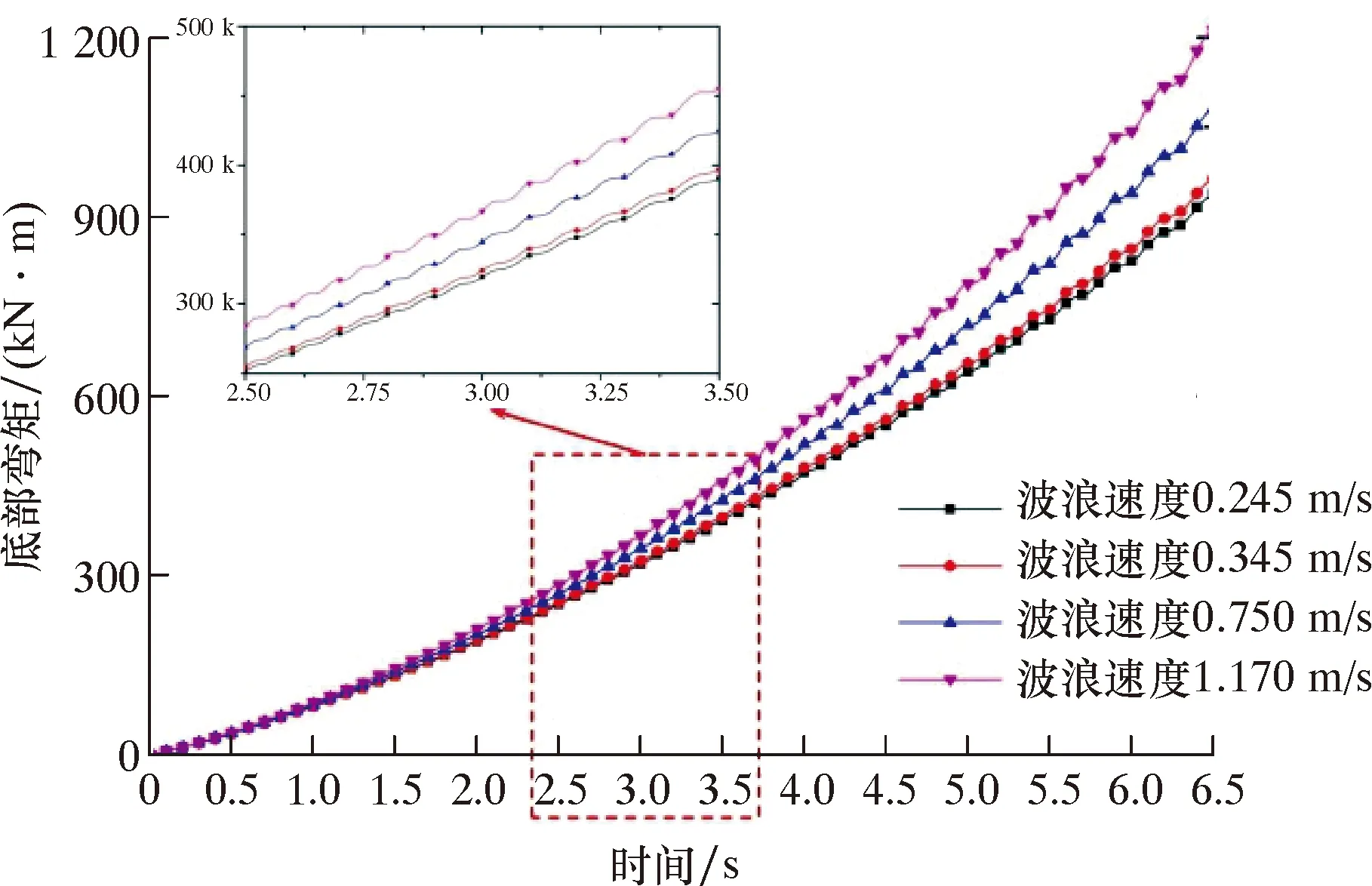
图8 不同波浪速度下立管底部弯矩变化过程图Fig.8 Variation of bending moment at the riser bottom at different wave velocities

表2 不同波浪载荷下立管最大位移及位置Table 2 Maximum displacement and position of the riser at different wave velocities

由图8可知，弯矩随着时间的变化呈周期性逐步增大，且弯矩波动幅度及最大弯矩均随海流速度的增大而增大，这主要是由于立管底部的位移引起底部转角改变，从而使弯矩产生变化。

3.2 立管壁厚影响分析

根据环境载荷及作业载荷变化，现场需合理选择立管厚度以保证立管作业安全，在保持拉力余量的基础上，进行了实例井管柱壁厚11.085、14.225、16.100、19.000 mm下的壁厚横向变形分析，获得不同壁厚下的立管最大横向位移分布及其对应水深如图9和表3所示，立管底部弯矩动态变化如图10所示。

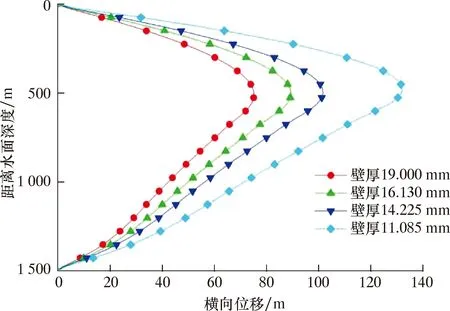
图9 不同壁厚下的立管最大横向位移Fig.9 Lateral maximum displacement of the riser with different wall thicknesses

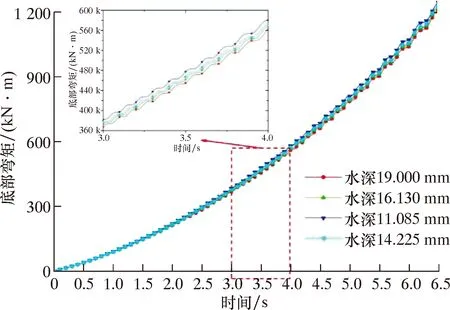
图10 不同壁厚下立管底部弯矩变化过程图Fig.10 Variation of bending moment at the riser bottom with different wall thicknesses

表3 不同壁厚下立管最大位移及位置Table 3 Maximum displacement and position of the riser with different wall thicknesses

由图9、图10可知，随着立管壁厚的增加，立管的最大位移减小，所处位置为自水下“”位置以上靠近水下“”；同时不同壁厚下弯矩整体变化过程呈周期性逐步变大，波动的形态基本一致；随着壁厚的增大，不同时刻立管底部的弯矩一定幅度减小，壁厚的增加使得管柱的截面惯性矩增大，提高了管柱的抗弯能力，因此立管的变形减小使得底部弯矩的值一定程度减小；但壁厚的过大会使立管张紧力增大，引起管柱上部拉力及拉应力的增大。

3.3 作业水深影响分析

随着全球海洋油气资源的勘探与开发水深的持续增大，掌握不同水深影响下的立管横向变形规律将为立管安全作业提供基础。基于此，本部分在保持张紧力系数一致的情况下进行了水深1 000～3 000 m下的立管横向动态位移分析，不同水深下的立管最大位移、位置及弯矩变化如图11和图12和表4所示。

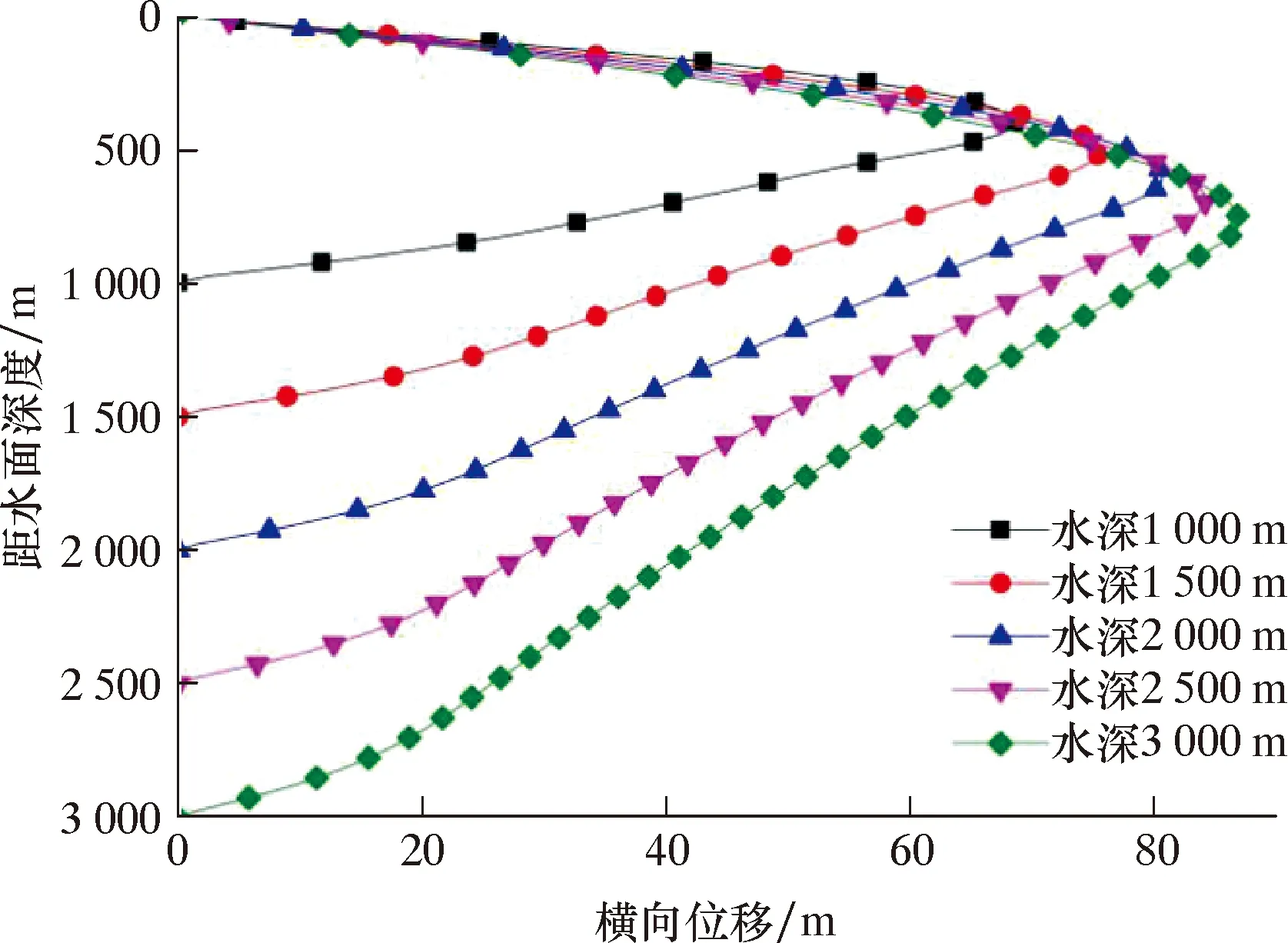
图11 不同水深下的立管最大横向位移Fig.11 Lateral maximum displacement of the riser with different water depths

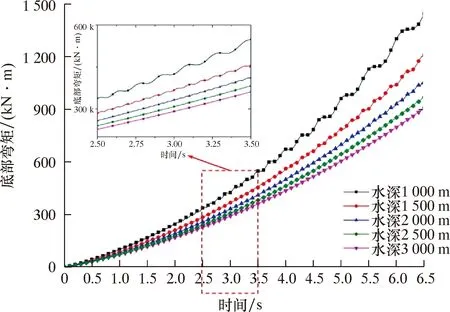
图12 不同水深下立管底部弯矩变化过程图Fig.12 Variation of bending moment at the riser bottom with different water depths

表4 不同水深下立管最大位移及位置 m

由相关结果可知，随着水深的增大，立管最大横向位移增大，位置整体位于水深“”附近，但是随着水深增大，最大位移自水深“”向海面靠近；此外，张紧力余量比例一致下，立管底部的弯矩变化波动周期减小、但变化幅度减小，是由于波浪载荷的主要影响海面200 m以内，200 m以上水深主要受海流影响，在波浪和海流综合影响下，立管上部受环境载荷更明显。