井筒温压场下微型测量器运移模型及校正研究*
2023-07-12廖星奥李军杨宏伟柳贡慧刘伟李牧廖茂林
廖星奥 李军,2 杨宏伟 柳贡慧,3 刘伟 李牧 廖茂林
(1.中国石油大学(北京) 2.中国石油大学(北京)克拉玛依校区3.北京工业大学 4.中国石油集团工程技术研究院有限公司 5.北京科技大学)
0 引 言
随着油气勘探开发的不断深入,剩余油气资源的开发难度越来越大,深部油气资源将逐渐成为勘探开发的重点,深井、超深井的数量必将越来越多[1-2]。然而在深井、超深井钻井过程中,容易遇到高温高压环境带来的钻井液性能不稳定、安全密度窗口窄、井壁稳定性差等难题,从而导致坍塌、卡钻、漏涌等井下复杂事故的发生[3-4]。近年来,因为随钻测量工具在钻井时通过与近钻头处的钻杆连接,能够测量井下温度、压力及钻井液物性参数,所以该工具及相关技术得以较快发展[5-7]。但随钻测量工具在实际钻井过程中存在使用费用较高,高温高压环境下易失效,发生复杂事故可能导致设备报废,深井全井筒信息无法实现实时测量等缺点[8]。因此研发价格便宜、耐温性好、能够全井筒测量的测量工具就显得尤为重要。笔者结合中石油工程技术研究院“井下微型随钻测量与数据监测分析系统基础理论研究”项目,选用研发费用低、耐温性好、能够全井筒测量的微型测量器(结构和工作原理与微芯片示踪器相似[9]),实现整个钻完井过程中快速、连续、低成本井筒多物理场(温、压、动、磁)协同测量,以期解决深井、超深井钻井测量过程中出现的难题。鉴于微型测量器只记录了物理场参数和对应参数的时间参数,没有记录与井深相关的参数,本文在S.F.CHIEN经验公式[10]的基础上,考虑井筒温压场的影响,建立微型测量器在井筒中的运移模型,并对微型测量器在井筒中运移的时间-深度关系进行校正研究。利用微型测量器的功能,可实时获取全井筒钻井液的流动状态及井筒温度压力剖面等信息,避免井下复杂工况的发生[11]。研究结论可为微型测量器的现场应用提供理论指导,并促进智能钻井技术的发展。
1 在井筒中的运移模型
选用的微型测量器如图1所示,其直径ds=10 mm、密度ρs=1.6 g/cm3,球形指数φ=1。
为建立微型测量器在井筒中的运移模型,设定如下假设条件:①微型测量器在井筒内运移的过程中不与井筒发生摩擦、碰撞;②微型测量器在井筒中的运移不受钻柱的旋转作用影响;③井筒中钻井液流速均匀。

图1 微型测量器结构示意图Fig.1 Schematic structure of the miniature measuring instrument
当微型测量器在井筒中运移时,作用于其上有2种力:一种是微型测量器受到的浮重(在流体中所受重力与浮力的合力);另一种是微型测量器在流体中流动时受到的阻力[12]。受力如图2所示。

图2 微型测量器运动过程中的受力图Fig.2 Force diagram of the miniature measuring instrument during wellbore transport
微型测量器在井筒中运移所受到的浮重计算式为:
(1)
式中:Wo、Fb及G分别为微型测量器在井筒中运移所受的浮重、浮力及重力,N;ρ为钻井液的密度,kg/m3;g为重力加速度,m/s2;γs为微型测量器重度,N/m3;γ=ρg。
微型测量器在井筒中运移受到的阻力计算式:
(2)
微型测量器在井筒中的受力与运移速度关系式[13]为:
Wo-R=ma
(3)
由式(1)、式(2)及式(3)得:
(4)

从式(4)可知,微型测量器的加速度等于其在流体中的浮重加速度与阻力加速度之差。当微型测量器从井口投入时,其运移速度为0,所受阻力也为0,这时运移加速度最大,等于它在流体中的重力加速度。此后受到流体的阻力作用导致运移加速度逐渐减小,一段时间后,微型测量器在流体中的阻力加速度与浮重加速度大小相等、方向相反,这时运移加速度为0,在井筒中处于等速滑落状态,相关研究把此时的速度称为等速滑落速度[14]vs。在外力平衡或者微型测量器以vs等速滑落时,由式(4)求解得:
(5)
但实际钻井液都具有一定的黏度,会影响微型测量器的运移速度,如图3所示。当运移速度较小,而钻井液黏度较大时,钻井液会在微型测量器周围呈现一定结构状态的绕流,从而降低运移速度。因此,黏度对微型测量器在井筒中运移的影响不可忽略。基于岩屑滑落相关研究,S.F.CHIEN考虑井筒中岩屑受力和黏度的影响,利用试验数据分析了当不规则颗粒滑落时阻力系数与颗粒雷诺数的关系,阻力系数与颗粒雷诺数及球形系数的关系式[15]为:

图3 微型测量器运移时受到黏度影响形成绕流Fig.3 Flow around the miniature measuring instrument attributed to viscosity during wellbore transport
(6)
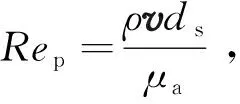
将式(6)代入式(5)中,得到岩屑滑落速度计算式:
(7)
式中:μa为钻井液黏度,Pa·s。
由式(7)可得:
(8)
其中:
(9)
式中:k为稠度系数,Pa·sn;n为流变指数。
由于所用微型测量器形状大小与岩屑类似,且球形系数为1,所以可用式(8)计算微型测量器在井筒内的运移速度。基于式(8),并考虑幂律流体黏度的影响,以此研究微型测量器在井筒中的运移速度的变化。其次,式(8)中ρ为常数,但根据现有研究,随着井深的增加,钻井液的密度会受到温度压力的影响,且该影响不可忽略[16]。因此,本文考虑了井筒温压场下钻井液密度变化对微型测量器在井筒中运移的影响。所用的钻井液密度模型为[17]:
ρL(p,T)=ρ0exp[4.331 7(p-p0)×10-10-
1.999(p-p0)2×4.733 8×10-4(T-T0)×
10-18-1.378 3×10-6(T-T0)2]
(10)
式中:ρL为钻井液随温度压力变化的密度,kg/m3;p为钻井液所受压力,MPa;T为钻井液所受温度,℃;ρ0为地面温度压力条件下钻井液密度,kg/m3;p0为地面压力,MPa;T0为地面温度,℃。
为研究钻井液密度随井深的变化规律,需先求得井筒温度压力剖面。基于井筒温压场计算模型的建立与求解思路[18],利用传热学理论分析钻柱内、环空内和地层间的传热问题,如图4所示。图4中Qa为地层传入环空热量;Qa(z)为环空轴向流出热量;Qa(z+Δz)为环空轴向流入热量;Qap为环空传入
管内热量;Qfp为管内热源项消耗热量;Qp(z)为管内轴向流入热量;Qp(z+Δz)为管内热源项轴向流出热量;Qfa为环空消耗热量;z+Δz为下一个网格位置。

图4 钻柱内、环空内、地层间的传热Fig.4 Heat transfer within the drill string,in the annulus and between formations
利用边界条件并结合有限差分法,得到地层和井筒传热模型:
(11)
式中:qm为质量流量,kg/s;CP为钻井液比热容,J/(kg·℃);β为传热系数,W/(m2·℃);r为距井眼轴线距离,m;z为井眼轴向距离,m;S为热源项,J。
井筒压力计算模型[19]:

(12)
其中:
(13)
式中:pc为井口回压,MPa;y为井深变量,m;h为井深,m;pf为单位摩擦压降,MPa/m;Dhy为水力直径,m。
结合式(11)、式(12)和式(13)3个模型,可建立井筒温压场计算模型,步骤如下:首先对井筒划分网格并进行离散化处理,设定边界条件后,利用有限差分法即可求解井筒温度剖面;接着利用钻井液密度模型及井筒压力计算模型求解井筒压力剖面;最后利用双循环迭代法对井筒温度剖面和压力剖面进行耦合,进而得到钻井液密度随井深的变化规律。井筒温度和压力剖面如图5和图6所示。钻井液密度随井深的变化关系如图7所示。

图5 井筒温度剖面图Fig.5 Wellbore temperature profile

图6 井筒压力剖面图Fig.6 Wellbore pressure profile

图7 钻井液密度随井深的变化关系Fig.7 Relationship between drilling fluid density and well depth
将求得的钻井液密度随井深的变化规律数据带入式(5),建立微型测量器在井筒中的运移模型。为研究井筒温压场对微型测量器在井筒中运移的影响,利用常规井参数,分别计算考虑井筒温压场影响的微型测量器在钻柱内运移速度随井深的变化关系,与不考虑井筒温压场影响的微型测量器在钻柱内运移速度随井深的变化关系,计算结果如图8所示。

图8 是否考虑井筒温压场影响的微型测量器在钻柱内运移速度的对比图Fig.8 Transport speeds of the miniature measuring instrument in the drll string with and without considering the influences of the wellbore temperature and pressure fields
由图8可知,考虑与不考虑井筒温压场影响计算的微型测量器在钻柱内的运移速度差别较大,在井底处误差值接近7%。因此,微型测量器在井筒中的运移需要考虑井筒温压场的影响。
建立微型测量器在井筒中的运移模型流程图如图9所示:

图9 微型测量器在井筒中的运移计算模型流程图Fig.9 Flowchart of the calculation model of wellbore transport of the miniature measuring instrument
2 在井筒中运移的校正模型
微型测量器在井筒中的运移是多维度运动,容易受到井壁不规则、摩擦及撞击等不确定因素的影响而改变运移速度,因此想要获得在井筒中运移的精确位置十分困难。为了提高微型测量器在井筒中运移速度的计算精度,在式(5)中引入速度校正系数x,得到校正后的运移速度:
vs,p=vl,p+xvs
(12)
式中:vl,p为钻井液流动速度,m/s;vs为未校正的运移速度,m/s。
速度校正系数x由UKF算法反演求解。利用UKF算法校正不同井深处微型测量器的运移速度,可以提高其在井筒中运移的时间-深度关系式的计算精度。
2.1 UKF反演算法
常规的卡尔曼滤波算法只能解决线性系统问题,但本文校正模型涉及流体力学计算,属于非线性系统问题。因此,本校正模型将UT变换(无迹变换算法)应用到卡尔曼滤波算法中,形成UKF反演算法,再依据观测量的变化关系反演出所需状态量的最优估计值,进而解决微型测量器在井筒中的运移模型涉及的非线性问题[20-23]。
2.2 在井筒中运移校正模型的建立
将速度校正系数x作为状态量,引入到微型测量器在井筒中的运移方程中,得到钻柱内微型测量器在井筒中运移的校正速度:
vs,p=vl,p+xpvs
(15)
环空内微型测量器在井筒中运移的校正速度:
vs,a=vl,a-xavs
(16)
式中:xp、xa分别为钻柱内和环空内微型测量器运移速度的校正系数。
UKF算法状态方程:
xk=f(xk-1)+wk-1
(17)
式中:wk-1为系统误差。
测量方程:
zk=h(xk)+vk
(18)
式中:vk为测量误差。
微型测量器在井筒中运移的校正模型流程图如图10所示。

图10 微型测量器在井筒中运移的校正模型流程图Fig.10 Flowchart of the correction model of wellbore transport of the miniature measuring instrument
校正计算过程中系统噪声和测量噪声的协方差分别设置为0.25和0.000 1。状态方程主要是对运移系统的预测,从而为下一个时间状态构造先验估计。测量方程主要是结合先验估计值和观测量(观测量是设定值)对当前状态的后验估计进行校正。
3 在井筒中运移校正模型的计算
获取微型测量器现场测量值可通过以下方法:微型测量器从井口投入,运移至钻头位置时,由于钻头喷嘴处直径小,会在短时间堵塞钻头喷嘴,导致沿管内轴向产生增压波,沿环空方向产生减压波(压力波传播速度极快,传播时间可忽略不计)[24];增压波传至井口后,立管压力迅速增大,可用立管压力的响应确定微型测量器到达钻头的时间,微型测量器在环空运移的时间可用套管压力的响应确定。因此,运用上述方法,设定测量值,研究微型测量器在井筒中运移的时间-深度关系。
选用实例井排量数据及相关参数计算微型测量器在井筒中的运移,排量随井深的变化如图11所示。
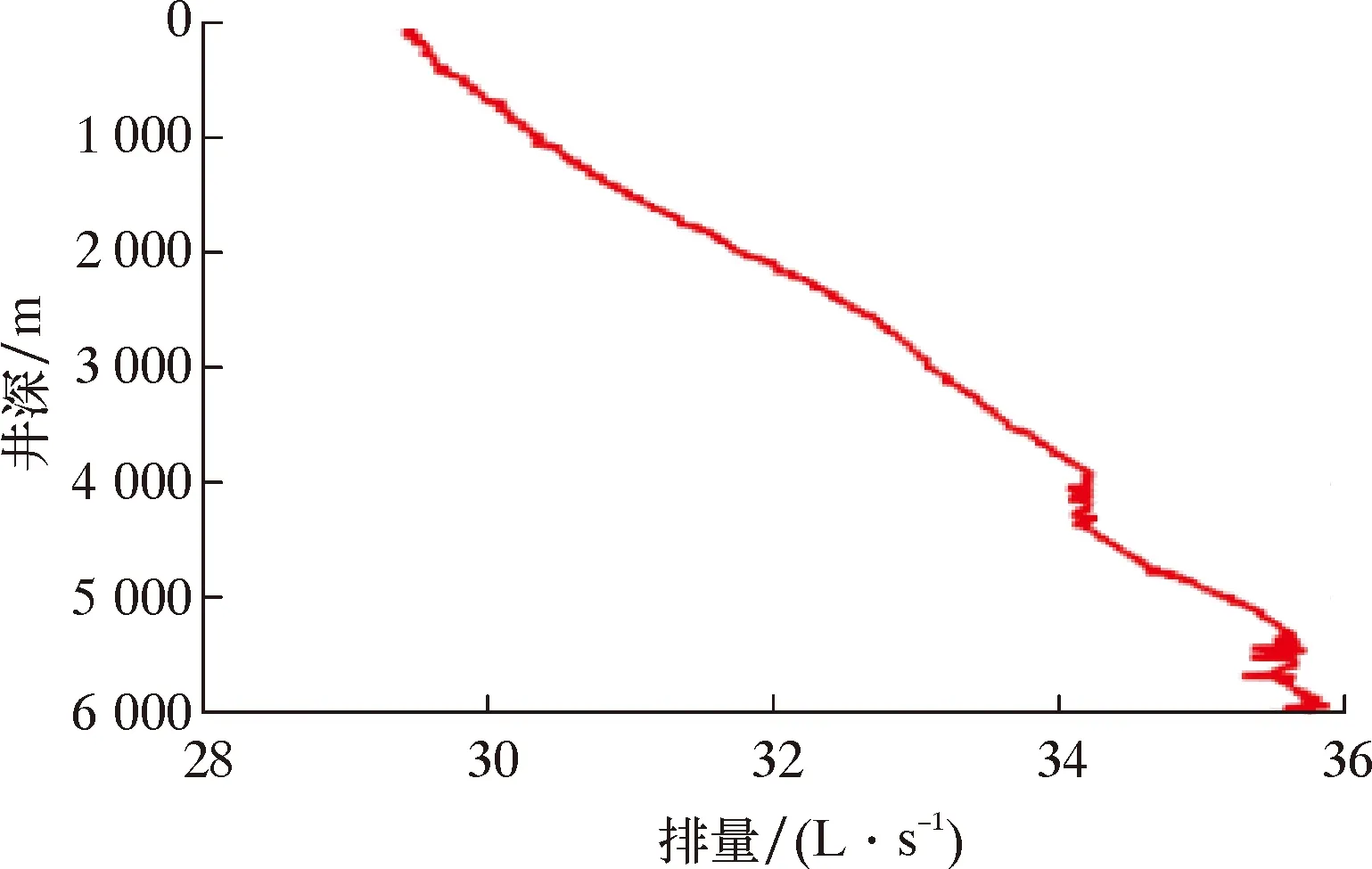
图11 排量随井深的变化Fig.11 Variation of pump rate with well depth
实例井相关参数如表1所示。
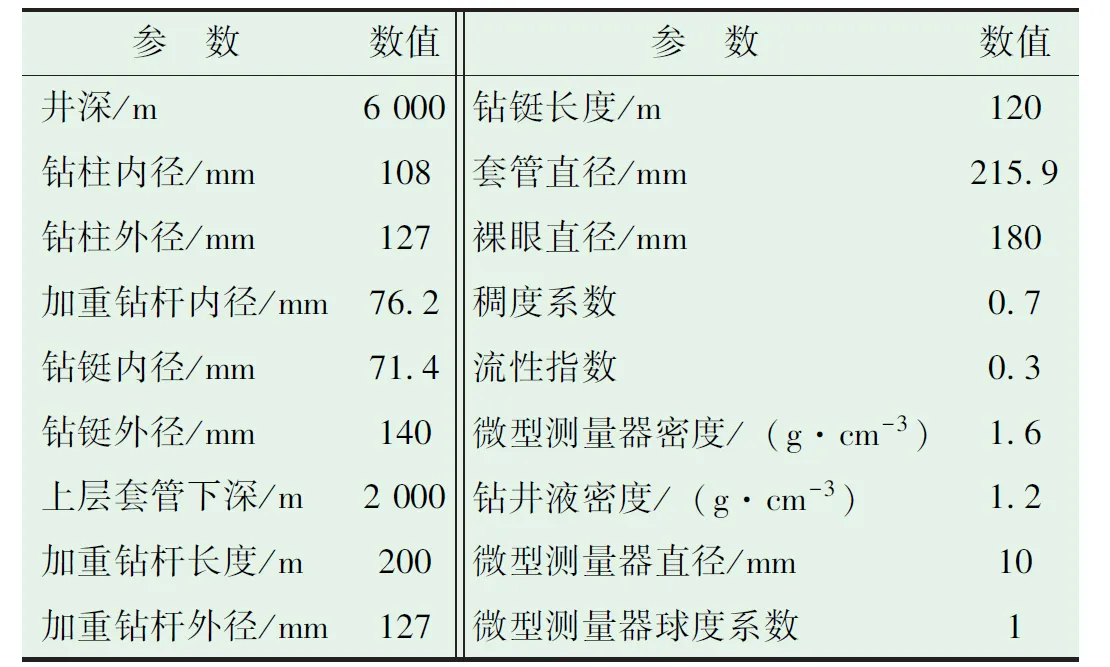
表1 实例井相关参数Table 1 Parameters related to the example well
为验证微型测量器在井筒中运移的校正模型对井下复杂因素影响的适应性,设定微型测量器在钻柱内0~5 680 m运移时的校正系数从1开始逐渐变大,斜率为0.001 m-1;因为钻柱内在5 680~6 000 m处直径变小,导致微型测量器在井筒中的运移更趋近于直线运动,所以设定校正系数增加幅度变缓,斜率为0.008 m-1。相应的,设定微型测量器在环空内0~2 000 m运移时的校正系数从1开始逐渐变大,斜率为0.001 m-1;因为在环空内2 000 m处,微型测量器从套管环空运移至裸眼地层,所以设定环空内2 000 m处校正系数发生突变,之后在裸眼地层2 000~5 680 m受到碰撞和摩擦的影响机率变大,设定校正系数变化幅度增大,斜率为0.001 5 m-1;因为在环空内5 680 m处,微型测量器的运移受井壁和裸眼地层的影响更大,所以设定环空内5 680 m处校正系数发生突变,之后在5 680~6 000 m处由于直径变小,导致微型测量器在井筒中的运移更趋近于直线运动,所以设定校正系数增加幅度变缓,斜率为0.000 8 m-1。微型测量器在钻柱内与环空内的运移校正系数随井深的变化如图12和图13所示。

图12 微型测量器在钻柱内运移校正系数设定值Fig.12 Transport correction coefficient of the miniature measuring instrument in the drill string

图13 微型测量器在环空内运移校正系数设定值Fig.13 Transport correction coefficient of the miniature measuring instrument in the annulus
将校正系数带入UKF算法观测方程即可得到观测量。为避免模型计算时间过长,确定离散后的网格长度为10 m,即每10 m进行一次反演计算。模型校正步骤如下:首先,在钻柱内和环空内根据微型测量器运动的总时间反演计算其运移速度校正系数;其次,在钻柱内和环空内根据微型测量器运移速度校正系数校正其在不同井段运移速度;最后,根据校正后不同井段的运移速度计算不同时间微型测量器所在井深。
处于钻柱内和环空内的微型测量器在井筒中运移速度的反演校正系数与设定校正系数的变化如图14和图15所示。由图14可知:钻柱内微型测量器的运移速度反演校正系数在0~5 680 m处始终与设定值相符,且误差逐渐减小;反演校正系数在5 680~6 000 m有小幅波动。由图15可知,环空内微型测量器的运移反演校正系数在0~2 000 m始终与设定值相吻合,且反演值逐渐收敛于设定值;当微型测量器从套管环空运移至裸眼环空时(即环空内2 000 m处),运移速度反演校正值波动剧烈,随着井深的不断延伸,反演次数逐渐增加,模型的反演校正系数逐渐收敛于设定校正系数;在5 680 m处,环空内微型测量器的运移反演校正系数有小幅波动以后逐渐趋于收敛。

图14 钻柱内微型测量器反演校正系数Fig.14 Inversion of the correction coefficient for the miniature measuring instrument in the drill string

图15 环空内微型测量器反演校正系数Fig.15 Inversion of the correction coefficient for the miniature measuring instrument in the annulus
微型测量器在钻柱内和环空内运移速度反演校正计算误差随井深的变化关系如图16和图17所示。由图16可知:微型测量器在钻柱内0~5 680 m,运移校正系数与设定值的相对误差逐渐减小,最大误差不超过2%;在5 680~6 000 m,由于设定校正系数变化较大,使得计算误差变大,但最大误差不超过0.5%。由图17可知:微型测量器在环空内0~2 000 m,运移校正系数与设定值的相对误差逐渐减小,最大误差不超过3%;在2 000~5 680 m,相对误差发生突变后逐渐变小,在5 680~6 000 m,相对误差发生突变后略微偏大,最大误差均不超过0.5%。
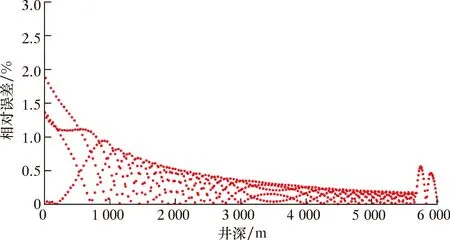
图16 钻柱内微型测量器反演校正计算误差Fig.16 Calculation error of the corrected transport of the miniature measuring instrument in the drill string

图17 环空内微型测量器反演校正计算误差Fig.17 Calculation error of the corrected transport of the miniature measuring instrument in the annulus
微型测量器在钻柱内和环空内运移的时间-深度关系如图18和图19所示。由图18和图19可知,随着井深增加,未校正的微型测量器运移的时间-深度关系与设定值差别越来越大,校正后基本趋于一致。

图19 微型测量器在环空内运移的时间-深度关系Fig.19 Time-depth relationship for the miniature measuring instrument when transporting in the annulus
综上所述,建立的校正模型不仅能够较准确地计算出微型测量器在井筒中运移的校正系数,而且能够根据井下情况实时调整计算结果。将反演得到的校正系数带入建立的运移模型,可以提高微型测量器在井筒中时间-深度关系式的计算精度。
4 结 论
本文结合S.F.CHIEN经验公式,并考虑井筒温压场的影响建立微型测量器在井筒中的运移模型;鉴于微型测量器在井筒中运移受井下多因素影响,建立基于UKF算法的微型测量器在井筒中运移的校正模型,并用实例井排量数据及相关参数进行了计算及分析。研究结论如下:
(1)考虑井筒温压场影响计算的微型测量器在井筒中的运移速度与不考虑井筒温压场影响计算的运移速度差别较大,且考虑井筒温压场影响更符合现场实际情况,因此研究微型测量器在井筒中的运移需要考虑井筒温压场的影响。
(2)校正后的微型测量器在井筒中运移的时间-深度关系式的计算精度受校正次数影响较大,校正次数越多,反演得到的校正系数越趋于稳定。
(3)利用实例井排量数据及相关参数计算,结果发现,微型测量器在井筒中运移的反演校正系数与设定值相吻合,建立的校正模型不仅能够较准确地计算出微型测量器在井筒中运移的校正系数,而且能够根据井下情况实时调整计算结果。
