Searching for QCD critical point with light nuclei
2023-07-11CheMingKo
Che Ming Ko
Abstract Density fluctuations and correlations due to a first-order quark-gluon plasma to hadronic matter phase transition and its critical end point, if they remain present after the hadronic evolution in a heavy ion collisions, can lead to an enhanced production of light nuclei in these collisions.This would then result in a non-monotonic collision energy dependence of the yield ratio NtNp∕N2d of proton number Np , deuteron number Nd , and triton number Nt.Measurements of this yield ratio as a function of collision energy thus provides the possibility to probe the equation of state of strong-interaction matter and its phase diagram.
Studying the properties of baryon-rich quark-gluon plasma(QGP) is the main focus of the beam energy scan (BES)experiments [1–3] at the Relativistic Heavy Ion Collider(RHIC) as well as at the future Facility for Antiproton and Ion Research (FAIR) and the Nuclotron-based Ion Collider Facility (NICA).There have been many theoretical studies on the QCD phase diagram and its structure, based on, for example, the lattice QCD [4], holographic models [5], and effective field theories [6].Also, the QCD phase diagram has been explored in the hydrodynamic framework by the BEST Collaboration [7] and used in machine learning methods to study its effects in heavy ion collisions [8].In particular,using the hydrodynamic [9–12] or transport [13] model with an equation of state that has a first-order partonic to hadronic matter phase transition, it has been shown that the produced matter in heavy ion collisions could be mechanically unstable due to the spinodal instability associated with the first-order phase transition.This would then lead to an amplification of the density inhomogeneity, and the resulting density fluctuations could enhance the production of composite particles, such as hadrons and nuclei, which can then be used as a signal of the first-order phase transition.For example, using a partonic transport model based on a three-flavor Nambu-Jona-Lasinio (NJL) model [14, 15] for Au+Au collisions with the initial quark temperature and density in the spinodal region of the corresponding stronginteraction QCD phase diagram, it was shown in Ref.[13]that the quark density fluctuation after the evolution would be larger for the case with a first-order chiral phase transition than for the case without a first-order chiral phase transition in the equation of state.These results are illustrated in panels(b) and (a) of Fig.1, respectively.
Also shown in Fig.1 are the light nuclei produced from the hadronic matter resulting from the clumping quark matter after hadronization and further evolution as well as their yield ratio Op-d-t=NtNp∕N2d, whereNp,Nd, and Ntdenote,respectively, the proton, deuteron, and triton numbers.According to Ref.[16], where the coalescence model [17–20] is used for light nuclei production, this yield ratio is related to the neutron relative density fluctuation Δn=〈(δn)2〉∕〈n〉2, with 〈n〉and 〈(δn)2〉being the average neutron density and its variance, respectively, byOne thus expects an enhanced Op-d-tif the neutron density fluctuation remains present at the kinetic freeze-out of produced hadronic matter.A similar density fluctuation effect on the yield ratio Op-d-talso holds if deuteron and triton are produced thermally or statistically at the kinetic freeze-out of the hadronic matter [21, 22].It was further argued in Ref.[23] that the critical fluctuations in the vicinity of the critical end point (CEP) of a first-order phase transition could also lead to an enhancement of the yield ratio Op-d-tas shown in Ref.[24].An enhanced Op-d-thas also been interpreted as a signal for the CEP according to Refs.[25, 26], which showed that light nuclei production would be enhanced as a result of their increased binding energies when the attractive part of nucleon-nucleon potential due to theσmeson exchange becomes deeper because of its decreasing mass as the system is close to the CEP.Reviews on this very interesting topic of the relation of light nuclei and the related topic of net baryon number fluctuations to the QCD phase transition can be found,respectively, in Ref.[27] and Refs.[28–30].For a recent review on experimental study of the QCD phase diagram in relativistic heavy ion collisions, it can be found in Ref.[31].
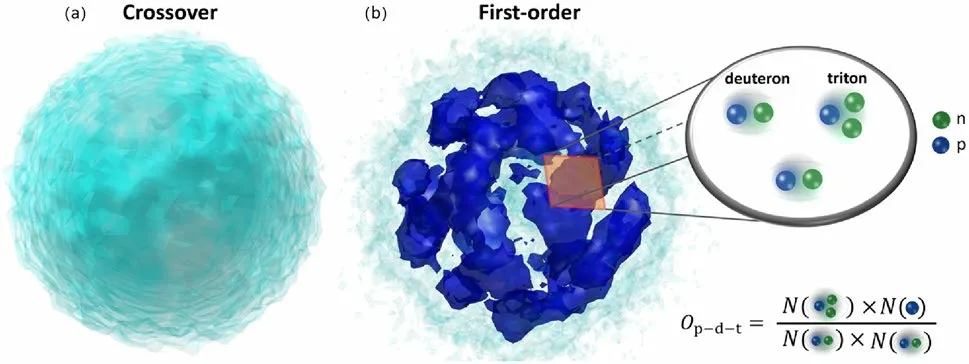
Fig.1 (Color online) Density distribution of strongly interacting matter in a heavy ion collision after its expansion for the cases of crossover transition (panel a) and first-order chiral phase transition (panel b).Also shown for illustration of the latter case are deuterons and tritons produced from the density fluctuating hadronic matter and their yield ratio Op-d-t =NtNp∕N2d , which depends on the magnitude of neutron density distribution as discussed in the text

Fig.2 (Color online) Collision energy, pT dependence of the yield ratio NtNp∕N2d in Au+Au collisions at RHIC for 0%-10% central (left panel) and 40%-80% peripheral (right panel) collisions.Dashed lines are the coalescence baselines obtained from the coalescence-inspired fit.Shaded areas denote the calculations from the MUSIC+UrQMD hybrid [32] and the AMPT [33] model.Taken from Ref.[34]
Recently, the STAR Collaboration has published in Physical Review Letters [34] the yield ratio Op-d-tfrom the data measured during the first phase of BES experiments.This result is based on the analysis led by Daniel Cebra, Matthew Harasty, Hui Liu, Xiaofeng Luo, Nu Xu, Ning Yu, and Dingwei Zhang.As shown in Fig.2 for Au+Au collisions in the center-of-mass energy range ofthis yield ratio is enhanced at 19.6 and 27 GeV in the most central collisions, although it shows a monotonic collision energy dependence.This result has been compared with theoretical predictions of the coalescence model for deuteron and triton production based on kinetically freeze-out protons and neutrons from microscopic models for relativistic heavy ion collisions.The latter include the hybrid model based on the (3+1)D viscous hydrodynamic model MUSIC for the quark-gluon plasma and the UrQMD transport model for the hadronic matter [32, 35] as well as a multiphase transport(AMPT) model that includes both the partonic and hadronic phases [33].With a smooth crossover transition between the quark-gluon plasma and hadronic matter, an essentially collision energy independent Op-d-tis predicted by these models for both peripheral and central Au+Au collisions.There have been attempts to extend the study of Ref.[13] based on the NJL model for the quark matter to include its hadronization and the evolution of the resulting hadronic matter via the AMPT model [21, 36].These studies have shown that the quark density fluctuation can largely survive hadronization but the hadron density fluctuation is somewhat washed out by their scatterings.The resulting yield ratio Op-d-tfrom the nucleon coalescence model based on kinetically freeze-out nucleons can, however, still be enhanced if the system goes through the spinodal region of the QCD phase diagram from the NJL model.Because of the low critical temperature and high baryon chemical potential in the NJL model, the enhanced Op-d-tonly happens in central Au+Au collisions at center-of-mass energies lower than where the peak is seen in the STAR data.More realistic models for the QCD equation of state are thus needed in this transport model study.These equations of state can also be used in the MUSIC+UrQMD hybrid model to study the collision energy dependence of Op-d-tand to extract the critical temperature and baryon chemical potential from the STAR data.

AcknowledgementsThe author thanks Xioafeng Luo, Yugang Ma, and Kaijia Sun for comments and suggestions, and also to Kaijia Sun for the preparation of Fig.1.His work is supported by the U.S.Department of Energy under Award No.DE-SC0015266.
杂志排行
Nuclear Science and Techniques的其它文章
- Resolution analysis of thermal neutron radiography based on accelerator‑driven compact neutron source
- Simple synthesis of silver nanocluster composites AgNCs@PE‑g‑PAA by irradiation method and fluorescence detection of Cr3+
- Photonuclear production of nuclear isomers using bremsstrahlung induced by laser‑wakefield electrons
- High‑precision high‑voltage detuning system for HIAF‑SRing electron target
- GOAT: a simulation code for high‑intensity beams
- Decomposition of fissile isotope antineutrino spectra using convolutional neural network
