Procedure for determining the number of thermal diffusion columns in square cascade for separation of Ne stable isotopes

Fatemeh Mansourzadeh ·Mohammad Mahdi Shadman ·Javad Karimi Sabet ·Valiyollah Ghazanfari

Abstract The thermal diffusion column represents one method of separating stable isotopes.This method is advantageous for smallscale operations because of the simplicity of the apparatus and small inventory, especially in gas-phase operations.Consequently, it has attracted attention for its applicability in tritium and noble gas separation systems.In this study, the R cascade was used to design and determine the number of columns.A square cascade was adopted for the final design because of its flexibility, and calculations were performed to separate 20Ne and 22Ne isotopes.All the R cascades that enriched the Ne isotopes by more than 99% were investigated, the number of columns was determined, and the square cascade parameters were optimized using the specified columns.Additionally, a calculation code “RSQ_CASCADE”was developed.A unit separation factor of three was considered, and the number of studied stages ranged from 10 to 20.The results showed that the column separation power, relative total flow rate, and required number of columns were linearly related to the number of stages.The separation power and relative total flow decreased and the number of columns increased as the stage number increased.Therefore, a cascade of 85 columns is recommended to separate the stable Ne isotopes.These calculations yielded a 17-stage square cascade with five columns in each stage.By changing the stage cut, feed point, and cascade feed flow rate,the best parameters for the square cascade were determined according to the cascade and column separation powers.As the column separation power had a maximum value in cascade feed 50, it was selected for separating Ne isotopes.

Keywords Stable isotope ·Thermal diffusion ·Cascade ·Separation ·Neon

1 Introduction

Stable isotopes are widely applied as precursors for radioisotopes and used in fields such as medicine, electronics,mineral exploration, metallurgy, industry, and physics research [1, 2].Understanding separation techniques would facilitate the production of a substantial of stable isotopes.Thermal diffusion is an important process because of its positive attributes, such as a high separation coefficient,simplicity, and cascade operation.Moreover, the apparatus involved is advantageous for small-scale operation because of its simplicity and small inventory, particularly for gasphase operations.Consequently, it has attracted attention for its applicability in tritium and noble gas separation systems[3, 4].This method produces expensive isotopes with high purity on a small scale (1–2 g of the target isotope per day at a concentration of over 99%).The temperature difference is the most crucial factor affecting mass transfer in a column.Separation using a temperature gradient was first conducted in 1938 by Classius and Dickel, who showed that high-effi-ciency component separation could be achieved by creating a convective flow using a temperature gradient [5].Over an extended period, Clausius et al.separated small quantities of the stable isotopes of chlorine, nitrogen, oxygen, carbon,and successfully separated many isotopes, including126Xe(33.6%),132Xe (17.5%),21Ne (99.6%), and20Ne (99.95%) [3,5].Other researchers have reported successful stable isotope separation using thermal diffusion columns.In 1960, Saxena and Watson optimized the physical parameters of a thermal diffusion column [6].In 1968, Rutherford et al.designed a column sample to compare the theoretical and experimental results of Ar, CH4, and Xe isotope separation and utilized a six-stage cascade to separate124Xe using 24 columns [2].Subsequently, in 1969, they experimentally and theoretically studied the isotopic separation of O2and N2in a thermal diffusion column [7], and in 1970, they examined the separation of21Ne column and cascade [8].In 1972, Roger and Rutherford designed a cascade to separate85Kr using a thermal diffusion column [9], and in 1979, Charles designed and investigated the ideal cascade of thermal diffusion [10].In 1981, Rutherford et al.analyzed the behavior of a cascade by changing the time required to separate multicomponent isotopes [11].In 1982, Zieger et al.optimized intermediate isotope enrichment in multicomponent systems [12].In 2003, Vasaru studied the separation of13C in a seven-stage cascade using 19 thermal diffusion columns, and investigated the enrichment of20Ne and22Ne in an eight-stage cascade comprising eight columns and86Kr and87Kr in a 15-stage cascade of 35 columns [13].From 1987 to 1997,Yamamoto et al.optimized parameters such as feed and pressure in a thermal diffusion column using analytical and experimental solutions for various noble gases [4, 14–17].In 2020, Saiki et al.investigated hydrogen isotope separation via thermal diffusion in a two-dimensional cascade of numerous small cavities [18].Furthermore, from 2014 to 2021, many researchers have studied numerical theories for multicomponent systems [19–22].

The thermal diffusion cascade was investigated in this study because of its application in noble gas isotope separation.The most notable approach to this problem involves determining the separating elements in a square cascade.Because of the importance of square cascades in separating multicomponent isotopes, determining the number of columns is necessary.To the best of our knowledge, although a considerable amount of research has been conducted, it has not been published.In the aforementioned studies, cascades with specific structures were used for isotope separation,and the number of columns for specific isotope separation was not specified.

The minimum total flow rate is the main criterion for determining the cascade stages and separation units, particularly when using analytical approaches [23].This is a typical and efficient approach.In situations in which the separation factor is high, determining the number of separation units using a numerical method is more accurate than using an analytical method.When the difference between the analytical and numerical results is large, previous studies have suggested using the numerical method for determining the number of separation units.Notably, the error also increases when the number of isotopes increases.Therefore, numerical techniques are essential in cascade design [20].

This study investigated the main concepts involved in designing cascades for separating stable isotopes using a thermal diffusion column.This procedure was used as an example for Ne isotope separation, and the match abundance ratio cascade (R cascade) was used to estimate the number of columns required.We modified the numerical algorithm presented in Ref.[20] and compared the analytical and numerical results, after which the required parameters were determined to evaluate the number of columns in the R and square cascades.Owing to its flexibility, a square cascade was then designed using the calculated columns.By changing the stage cut, feed point, and cascade feed rate,the best parameters for the square cascade were determined according to the cascade and column separation powers.To this end, cascade modeling and design methods for thermal diffusion columns were identified, and calculation codes for the cascade design were prepared.

2 Research theories

The common R and square cascades are shown in Fig.1.The feed mixture (F) with compositionzi,Fenters a cascade.The cascade then delivers the heavy product (W) and lightproduct (P) with compositionsxi,wandyi,p, respectively.Stagesreceives the feed flow rateZsand delivers the up and down flow ratesMsandNs,respectively [19–21].

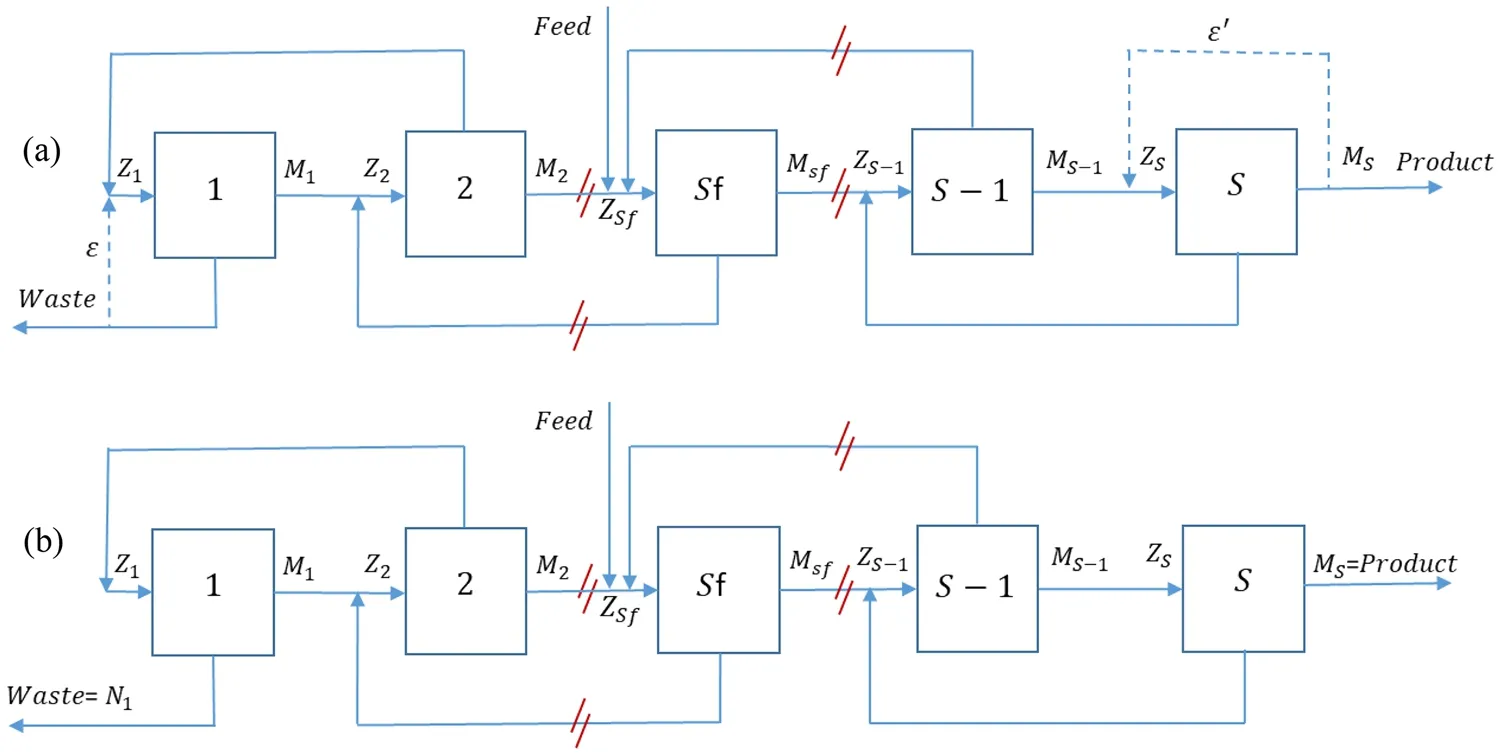
Fig.1 a Square, and b R cascades

The governing equations are listed in Table 1.The total number of stages isS, and the number of components in the feed mixture isNc.In square cascades, the number of separation units and feed flow rateZsare constant in each stage(Eq.1).In contrast to the square cascade, the rate of return flows ε and ε' in the R cascade is zero [21].

Equations 1–7 show the gas flow rates in cascade pipes[20–22].Equations 2–5 show the mass flow balance at the mixing points from 1 toS.In these equations, the cut in each stage isθs.Equations 6 and 7 can be obtained using the mass flow balance in each stage and the definition of cut in stagess

Equations 8–15 show the concentrations of isotopes in the cascade stages.Equation 8 shows the mass conservation of the isotopeith in the stagesth, and Eqs.9–12 shows the mass balance of the componentith at the mixing points.αij,sis the separation factor between the isotopesith andjth at thesth stage (Eq.13), andα0is the overall separation factor for the unit mass difference.MiandMjrefer to the molar weights of theith andjth isotopes, respectively.Finally, the concentrations must satisfy the constraints in Eq.14 [20–22], that shows the sum of the concentrations of each component at the mixing points should be equal to 1.

In the R cascade, the match abundance ratio for the two isotopesk1andk2is defined using Eq.15 [20, 21].The parametersR,R′ andR″ are the abundance ratios in the feed, light, and heavy flows, respectively (Eq.16).Previous studies have shown that the R cascade is suitable for thermal diffusion cascade design, such as the gas centrifuge cascade[10, 24].

The analytical approach to the R cascade is as follows[21, 23, 25]:

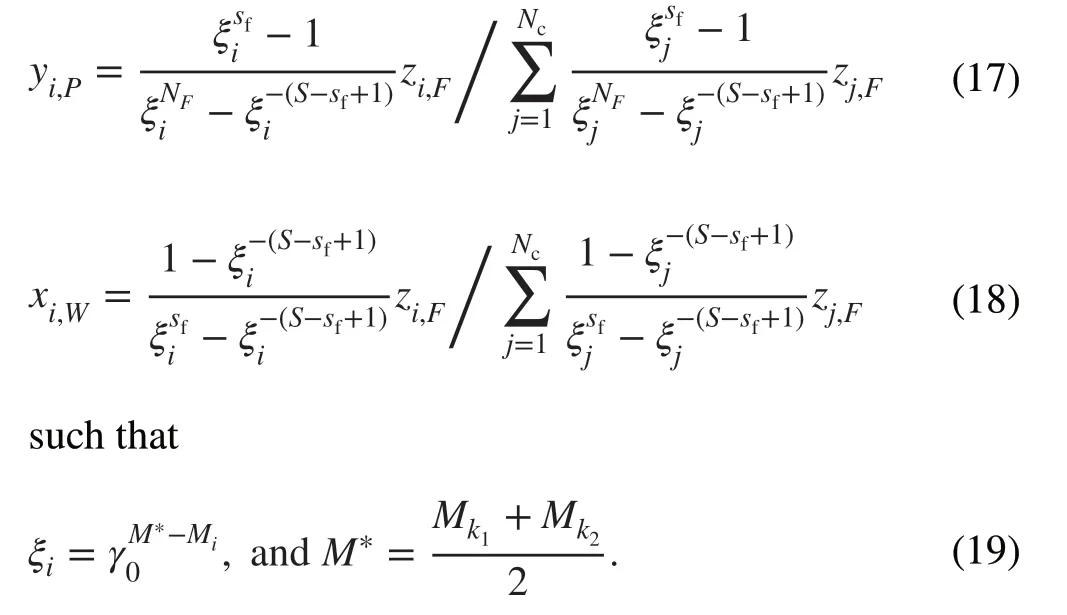
The number of stages (S) and feed stage (sf) with the given external isotope concentrations (yk,P,xk,W) can be obtained by solving Eqs.(17) and (18).The feed flow rate at each stage (Zs) can be obtained using Eq.20.

Based on Eq.20, the parameterZsdepends on ξi,and according to Eq.19, ξiis a function ofM*.Hence, the cascade parameters for isotopesk1andk2can be determined.IfM* is used as an optimization variable and hasa value between the actual components (M1≤M∗≤MNc),there is a continuous set of cascades.

Table 1 Governing equations in the square and R cascades

2.1 Separation power

The separative power was calculated using Eq.(21).

whereF,P, andWare the flows of the feed, light, and heavy products, respectively, andyi,P,xi,W, andzi,F, are the corresponding isotopic concentrations.Moreover,V(c1,c2,…cNc)is the separation potential of the multicomponent system.

There is no standard interpretation of the separation potential of multicomponent systems despite the many approaches devised for its evaluation.Thus far, relationships have been introduced for separation potentials based on different assumptions.If a small number of impurity isotopes are present in the feed and the two components are the main isotopes, the most suitable potential relation is [26].

whereciis the isotopic concentration of the product, waste,or feed streams, andk1andk2are the indices of the main isotopes.

3 Calculation procedure

First, different R cascades and their effects on the separation of20Ne and22Ne were studied, and a cascade design was performed.Consequently, the required number of columns was estimated using the R cascade.Subsequently, a square cascade with specific columns was determined and optimized for the separation of Ne isotopes.

In this regard, the computational code “RSQ_CASCADE”was developed, and the required number of columns was determined to bey20Ne,P>99% , andx22Ne,W>99% by changing the number of R-cascade stages from 10 to 20.The concentrations of Ne stable isotopes in the feed stream werez1,F(20Ne)= 0.9048,z2,F(21Ne)= 0.0027, andz3,F(22Ne)= 0.0925.The componentsk1andk2in the R cascade were20Ne and22Ne , respectively.

The parameters that determine the number of stages were separation power, number of columns, and relative total flow(product flow ratio to total feed flow).In this study, the unit separation factor and feed flow rate of the thermal column were 50–60 cm3/s and 3, respectively.These parameters were obtained from experimental data [15].

The numerical procedure for the RSQ code is shown in Fig.2.This code consists of two separate sections for modeling the R cascade (Fig.2a) and the square cascade (Fig.2b).

3.1 R cascade

The differences between the numerical and analytical total flow values for various alphas are listed in Table 2.When the separation factor increases, the difference between analytical and numerical methods for determining the value of∑Zincreases.Therefore, we used numerical methods to calculate the separation elements.Notably, these results are for Ne isotopes, and additional changes occur as the separation factor increases for other isotopes.For example,∑Z∕Pfor the separation of78Kr using an analytical solution was 2791.2 [25], which is equal to 2863.63 for the numerical calculation and leads to a 2.5% error.This result corresponds to a unit separation factor of 1.1.Therefore, the number of separation units was numerically determined in this study.

Table 2 Calculated total flow rate values for the numerical and analytical methods in different alphas

The R cascade was simulated as described in Ref.[20];however, only the solving of nonlinear equations, and the equation for the continuation technique in it is based on the Newton method and the definition of enrichment factor.A comparison of the two algorithms showed that the convergence time and number of loops required were reduced.Replacing the Newton method with a trust region and changing the homotopy equation reduced the number of required iterations from 1322 to 47.If only the trust region was used without changing the homotopy equation, the iteration convergence was reduced from 1322 to 687.

3.2 Square cascade

As mentioned before, in the simulation of the square cascade,Zsis known and provided as the input.Moreover, the parametersMs,Ns, ε, and ε' are unknown.Therefore, there are 2S+ 2 unknown parameters.The independent equations, which include the equations of flow at the stages and mixing points,are 2S.In solving these equations, two parameters must be determined.In a square cascade, the cut is the most significant operational parameter.Having the cut in the first stage and the cascade cut, the flow rates are obtained using Eqs.(1)–(7)[21].Additionally, using nonlinear Eqs.(8)–(13), the concentration of isotopes is determined using the Q-iteration method explained briefly in this study.

By extracting the parameterzi,sfrom Eq.(8), and replacing it with Eqs.(9) and (10), Eqs.(25)–(28) are obtained in terms ofxi,s.

In these relations,yi,s=qi,sxi,s, and considering this definition for Eq.(13), Eq.(29) is obtained as follows:

First, the value ofqj,sis estimated for all stages; subsequently, it is calculated in all stages using Eq.(29).Therefore, the nonlinear Eqs.(25)–(27) are linearized, and the value ofxi,sis calculated for all stages.Subsequently, the value ofyi,sis calculated from the definition ofqi,s.Additionally,zi,sis determined by considering the conservation equations for the isotopeith in the stagesth.By applying Eq.14, the error value is checked at each calculation step,qi,sis modified, and the calculations are repeated.More detailed explanations are provided in Ref.[27].Although the principles remain the same, the equations differ.

4 Results and discussion

4.1 Results for R cascade and column number estimation

The number of stages in the R cascade was changed from 10 to 20.Figure 3a shows that an increase in the number of cascade stages decreased the column separation power.This parameter varied from 27.48 to 26.95 (sccm).The column separation power for the 10-stage cascade was slightly higher than other R cascades.

Fig.3 a Column separation power, b column number, c light relative total flow, and d heavy relative total flow according to the number of stages

As shown in Fig.3b, the number of columns increased from 85 in the 10-stage cascade to 105 in the 20-stage cascade.Despite the increase in the number of columns and stages, the column separation power did not change considerably.Moreover, the flow rates of light and heavy products largely remained constant.However, as shown in Fig.3c and d, the relative total flow rate decreased as the number of stages increased.The light relative total flow isProduct∕∑S s=1Zs, and the heavy relative total flow isWaste∕∑S s=1Zs.Notably, the waste in this study is related to the flow rate of the22Ne product stream that withdraws from Stage one.This phenomenon indicates that the total flow rate increases as the number of stages increased.Therefore, the best choice is a cascade with 10 stages, fewer columns, and better separation power than other R cascades.Moreover,reducing the number of columns decreases operating costs while improving separation efficiency.Therefore, because of the same light and heavy products, the same enrichment,and greater column separation power the R cascade with 85 columns was selected.

4.2 Results for square cascade

A square cascade with 85 columns was investigated based on R cascade studies.The square cascade comprised 17 stages,with five columns in each stage.By changing theθs,sf, andF, the square cascade parameters were determined according to the cascade separation power and column separation power.Owing to their flexibility, these parameters in the square cascade can change each time.Table 3 presents the main parameters of the optimal squared cascade.

As mentioned above, the optimal feed rate value was 50–60 sccm.Therefore, the input flow rate for all stages was 250–300 sccm.Thus, changes could only be observed regardingθs,sf, andFincreasing the enrichment of both Ne-20 and Ne-22 to 99%.A suitable value for the stage cut was considered to be close to 0.5.

As the feed rate increased, the amounts of light and heavy products in the cascade increased.Moreover, with an increase in the cascade feed flow rate, the column separation power reached a maximum of 27.8 (cm3/min) at 50 sccm and then decreased (Fig.4a).In contrast, as shown in Fig.4b, the cascade separation power increased as cascade feed increased.Therefore, the higher the feed rate, the better the yield and separation capacity.

In the cascade design, a pressure-regulating valve must be used at each stage to separate the desired isotopes according to the operating conditions of the column.Thus, adjusting the cut to a certain value is possible, and the separation can be performed.If the design constraints can be overcome,cascade 5 is more suitable because of its greater cascade separation power and higher product (with an increasing cascade feed rate, the cut deviation rate increases from 0.5).Otherwise, cascade 3 seems more suitable than other R cascades because of its higher column separation power.

Nevertheless, the correct and optimal use of the cascade in isotope separation depends on the preparation of the operational documentation of the column and the effects of the parameters on the separation factor.

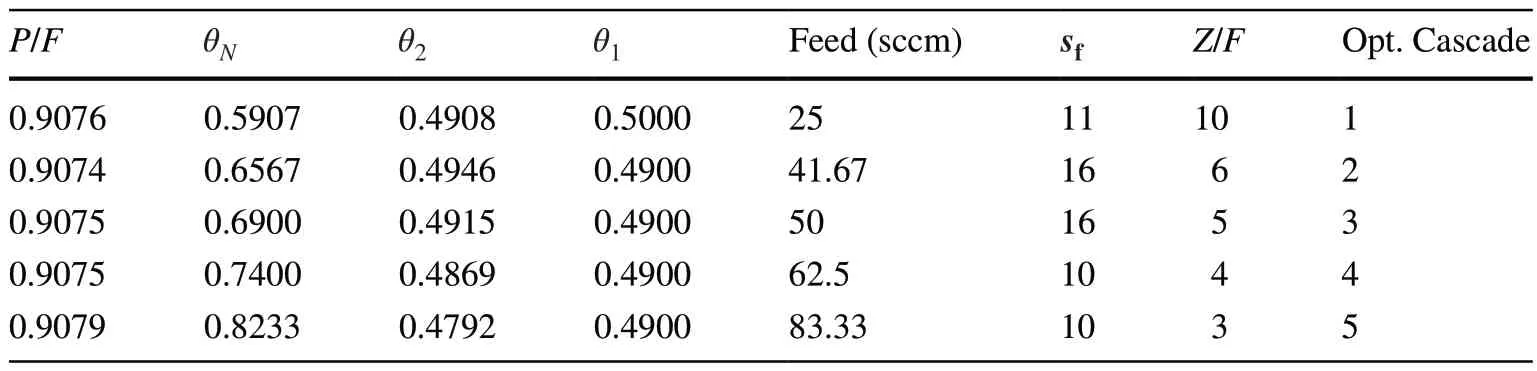
Table 3 Main square cascade parameters

Fig.4 Variation in a column separation power and b cascade separation power according to the square cascade feed rate

5 Conclusion

In this study, a thermal diffusion column cascade was investigated to separate Ne stable isotopes.Owing to the difference between the numerical and analytical total flow values for various alphas, numerical method to calculate the separation elements in the R cascade.Therefore, two calculation codes were developed in MATLAB.Subsequently, the thermal column separation power and the light and heavy relative total flow rates were studied in the R cascade from stages 10–20 to determine the required column numbers.The results suggest a 10-stage R cascade with 85 columns to separate stable Ne isotopes.The R cascade is better than the square cascade for separating stable Ne isotopes because of its proximity to ideal conditions.Because different cuts are required in all stages, single-column tests should be performed according to these requirements.

In the long term, in separating other isotopes of noble gases, a square cascade should be used because of its flexibility.Subsequently, a square cascade was designed, and the calculations resulted in a square cascade with 17 stages and five columns for each stage.

Conflict of interestThe authors declare that they have no competing interests.