An online fast multi‑track locating algorithm for high‑resolution single‑event effect test platform

Yu‑Xiao Hu ·Hai‑Bo Yang ·Hong‑Lin Zhang ·Jian‑Wei Liao ·Fa‑Tai Mai ·Cheng‑Xin Zhao

Abstract To improve the efficiency and accuracy of single-event effect (SEE) research at the Heavy Ion Research Facility at Lanzhou,Hi’Beam-SEE must precisely localize the position at which each heavy ion hitting the integrated circuit (IC) causes SEE.In this study, we propose a fast multi-track location (FML) method based on deep learning to locate the position of each particle track with high speed and accuracy.FML can process a vast amount of data supplied by Hi’Beam-SEE online,revealing sensitive areas in real time.FML is a slot-based object-centric encoder–decoder structure in which each slot can learn the location information of each track in the image.To make the method more accurate for real data, we designed an algorithm to generate a simulated dataset with a distribution similar to that of the real data, which was then used to train the model.Extensive comparison experiments demonstrated that the FML method, which has the best performance on simulated datasets, has high accuracy on real datasets as well.In particular, FML can reach 238 fps and a standard error of 1.6237 μm.This study discusses the design and performance of FML.

Keywords Beam tracks ·Multi-track location ·Rapid location ·High accuracy ·Synthetic data ·Deep neural network ·Single-event effects ·Silicon pixel sensors ·HIRFL

1 Introduction

Various high-energy radiation particles such as protons,electrons, alpha particles, and heavy ions exist in the space radiation environment [1].The single-event effect (SEE) is a process in which space-energetic charged particles in the sensitive region of a device [2] cause a change in the logic state of the device, directly leading to device damage or even complete failure.SEEs are classified as single-particle flip,single-particle lock, single-particle transient, etc., according to the phenomenon; SEE is a general term that includes all single-event effects.Advanced semiconductor devices and large-scale integrated circuits are widely used currently, with the development of semiconductor technology.Electronic systems in aerospace, aviation, and missile devices must consider the hazards of SEEs [3–5].

Ground-based SEE test facilities are common tools for evaluating devices’sensitivity to SEE [6, 7].This experiment has the advantages of a short cycle time, low cost, and greater flexibility than the on-orbit experiment.Heavy ion,proton, and neutron beams are commonly used in ground radiation test facilities [8].In ground simulation tests, the sensitive regions where single-particle effects occur in the devices to be tested must be precisely determined so that the radiation-resistant design of integrated circuits can be targeted and reinforced.

Beam monitors are primarily divided into two types of structures: interceptive [9–11] and non-interceptive [12–14].Interceptive beam monitors can provide real-time data on the beam cross section, flow intensity, and location.For example, Faraday cups [9] use a charge collection plate to capture the particle beam charge directly; scintillator screens [10]are combined with a charge-coupled device (CCD) camera for observing the beam spot, which is a very simple and reliable monitor of the beam profile; and optical transition radiation screens [11] determine the beam profile by detecting electromagnetic radiation from a metal foil.However,when in use, they may turn off the beam at the detector and dismantle the beam structure, making the beam unavailable to the equipment at the back-end of the system, which cannot provide an online measurement of the beam profile.Noninterceptive beam monitors can measure the beam profile,center position, and other information without disturbing the beam structure.For example, beam transformers [12] use a transformer to capture the magnetic field associated with the beam and generate the corresponding voltage, whereas residual gas ionization monitors [13–15] perform almost nondestructive beam profile measurements by collecting ionized particles.Non-interceptive beam monitors not only cause minimal structural damage to the beam, but also effectively extend the life of the detector and enable online measurements owing to the use of indirect measurement techniques because offline analysis needs to store a large amount of data[19] and consumes huge storage space, which is unrealistic.

To meet the beam monitoring requirements at the HIRFL and HIAF, we propose a series of Hi’Beam detection systems [16–19], including HiBeam-A [16, 17] for the accelerator, Hi’Beam-T [18] for the physics terminals, and Hi’Beam-SEE for the SEE terminal at the HIRFL.The Hi’Beam series was implemented based on pixel sensors because of their high-accuracy position resolution, short response time, and fast readout.In this study, we focused on the Hi’Beam-SEE system, which is used to locate the region where SEEs of the Device Under Test (DUT) occur.The structure of Hi’Beam-SEE is shown in Fig.1.The system consists of two pixel detector units with the same structure, but independent of each other and placed perpendicular to each other.Each detector unit contains a cathode plate and a Topmetal-M[20, 21] chip that acts as an anode plate.A uniform electric field perpendicular to the electrodes is provided between the two electrodes in each cell.The DUT was placed on the right side of the detector.As heavy ions pass through the detector,they collide with the air along their tracks, creating electronion pairs.Driven by an applied electric field, the electrons drift toward the anode and are absorbed, and the projection of the ion track in two vertical planes is obtained through the top metal chip, which is used to reconstruct the spatial position of the beam to infer the hit point of the ion at the DUT.The Hi’Beam-SEE system is a heavy-ion beam monitoring series facing the terminal of a SEE test at HIRFL, which needs to have a measurement accuracy of 2–3 μm; therefore,we implemented the first version of the Hi’Beam-SEE based on the Topmetal-M chip.The Topmetal-M [20, 21] chip was the first Monolithic Active Pixel Sensor designed using China’s domestic process for heavy ion physics.Subsequently,we plan to use our self-developed Nupix-S pixel chip, which can achieve an event rate of 10 kHz.In particular, we verified the track localization of the V0 version based on Topmetal-M through preliminary tests and achieved an expected accuracy of approximately 1.6 μm [21].

Fig.1 (Color online) Typology of the Hi’Beam-SEE system

However, current track location methods can only record each frame of data and then locate the track offline.For the final online real-time monitor, the data volume of the current methods is very large, and we only need to record the key information (slope and intercept) of the track in each frame; therefore, an efficient online tracking algorithm is required.With an event rate (particle flux) of 10 kHz and an SEE probability of approximately 1/50, our algorithm must have a processing speed close to 200 fps.In addition,another challenge of trial localization is the need to locate multiple tracks simultaneously in one frame, which is one of the bottlenecks of traditional methods; therefore, we consider neural networks.Highly accurate multi-track location is a challenge that must be overcome.Currently, with the present time of rapid development of deep neural networks,several track location algorithms can be applied to beam location tasks.Deep neural networks are not limited by the number of objects to be detected and exhibit very high accuracy.In addition, well-trained neural networks can provide rapid results.Therefore, it is natural to introduce deep neural networks.In addition, deep learning requires a relatively large amount of data.We propose a method for generating simulated beam data that aids in training to obtain a more robust neural network model.In our experiments, we show that the model developed by training on the simulated dataset still performs well on a real dataset.

In this study, based on Topmetal-M and Hi’Beam-SEE,we designed a method to generate simulated data and provide a fast multi-track location (FML) method to precisely locate the projected tracks.Specifically, the traditional methods and related studies are discussed in Sect.2.In Sect.3 we propose a novel multi-online tracking algorithm for the Hi’Beam series beam monitor, which includes designing a method to simulate the beam data such that the generated data have a similar distribution of gray values as the real data; additionally, we propose a fast method FML to locate one or several ionization tracks by deep learning.Extensive comparative experiments are presented in Sect.4, which include the locations of a single track, multiple tracks,and real tracks (single real track and multiple real tracks).Finally, Sect.5 summarizes our study.Our main contributions can be summarized as follows:

• We designed a fast method, namely, FML, for detecting ionization tracks by deep learning that is nearly 10 times faster than traditional algorithms.By applying this algorithm, we achieved the fast location of single-particle effects in conjunction with hardware systems, thus enabling near real-time location of sensitive areas of singleparticle effects.

• Unlike the traditional methods that are effective only for a single track, the proposed FML can detect multiple tracks with high accuracy.FML is no longer limited by the number of tracks and has better application prospects.

• We designed a method to generate simulated beam data,which is very similar to real data.This simulated dataset greatly expands the beam data to provide strong support for simulation experiments.We verified experimentally that this method, which has good accuracy on simulated datasets, has the same accuracy on real datasets.

• The proposed FML method greatly improves the accuracy of track location compared to other methods not only on simulated datasets but also on real datasets.

2 Related work

2.1 Track location methodology

2.1.1 Mass center method

The mass center method [22] is the most common method used today.This method takes the mass center of the column within the vertical range of the pixel, which is the highest gray value in this column, and then uses the mass center of each column to fit the final predicted track.This method is simple, but has major limitations.First, this method is highly sensitive to noise.The determination of the center’s position determines the accuracy of the mass center method.However, it is difficult to avoid noise when the device is functioning, and the intensity of noise always depends on the uniformity of the electric field and the type of gas [16,17].The mass center method does not exclude these extraneous noise points when calculating the mass center position;therefore, the position is inaccurate.This method becomes more unstable and significantly reduces the accuracy of the results, particularly when the noise is not evenly distributed.Second, the mass center method does not work in the case of numerous tracks.Two or more tracks are frequently observed in the original dataset.Pixels with high gray values are dispersed in various regions of the same column when the image consists of many tracks.Because the mass center method takes only one pixel with the highest gray value in each column, the location of the mass center of this column is determined within a small area perpendicular to that pixel.Therefore, in the case of multiple tracks, the center of mass is often located on one track with a higher gray value,and the other tracks are completely ignored.When the pixels with the highest gray values in various columns correspond to various tracks, the issue worsens.At this point, the results obtained by the mass center method will be extremely confusing.Even if the total number of tracks is known in advance, this method cannot accurately determine the mass center of each track, which significantly affects the outcome of the fitting process.In addition, the mass center method is time-consuming and labor-intensive.Because the track does not span the entire image, it is not necessary to find the center of mass in the column where the track does not appear.Therefore, the column where the track occurs must be manually located before computing the center of mass,which is quite difficult.

2.1.2 Double edge detection method

The double edge detection method is different from the mass center method, which uses the amplitude intensity of the track image as the confidence level of whether the pixels belong to the track.The double edge detection method uses the gradient information of the image to determine whether a pixel point belongs to a track.Owing to the diffusion of the electron cloud, the tracks form a strip pattern with a certain width on the image.Because there is a significant difference in the gray values between the track and background,there is a sudden change in the gray value at the edge of the track, and this change is the gradient information of the track.Inspired by the gradient information of the track,this method does not directly localize the tracks, but first finds the edges of the tracks based on the apparent gradient information.Then, this method determines the number of traces using the Hough transform and uses an edge detection algorithm, such as the Canny edge detection method[23] to obtain the features of the boundaries on both sides of the tracks.The centerline between the two boundaries is the track projection predicted using the double edge detection method.Compared with the mass center method, this method can better handle multi-track situations and provides the information of each track separately.Additionally, this method is not easily affected by distant noise.

However, when using this method, it is difficult to determine the parameters of the algorithm, particularly the segmentation step size of the distance and angle in the Hough transform [24].A very large segmentation step size will lead to insufficient precision.If the segmentation step size is very small, the accumulated energy values of each lattice point in the Hough space will be relatively close, which will cause difficulties in the subsequent non-maximum suppression algorithm.This is unreasonable because the quality of the prediction results is highly dependent on the choice of parameters.Additionally, parameter selection in the nonmaximum suppression algorithm is extremely important.If it is not properly selected, some edges will either be missed or false edges will appear.In addition, the double-edge detection method does not improve the calculation speed compared to the mass center method.

2.2 Deep neural network

Since Alex Krizhevsky proposed AlexNet [25] in 2012,GPU-based convolutional neural network (CNN) models have achieved great success and led to the rapid proliferation of deep learning.With the rapid development of computers, deep learning [26] has been widely used in many fields including physics, chemistry, life science, and medicine[27–30].Deep neural networks (DNNs) constitute the basic framework of deep learning and require networks containing multiple hidden layers [31].Thus, DNNs can discover the distributed feature representations of data by combining low-level features to form more abstract and higher-level representations of attribute classes or features.The core of DNNs is to learn more useful features by building machine learning models with many hidden layers and large amounts of training data to improve the accuracy of classification or prediction.Specifically, DNNs learn a deep nonlinear network structure using a backward gradient propagation algorithm and numerous parameters to approximate complex nonlinear functions, allowing them to interpret data similar to the human brain.DNNs simplify classification or prediction tasks by transforming the feature representation of samples in the original space into a new feature space through layer-by-layer transformation [32].Compared to the manual rule-based method of constructing features, using a large amount of data to learn features is more capable of portraying the rich intrinsic information of the data.DNNs have also been widely used in the field of imaging, where they have demonstrated remarkable capabilities in classification, detection, segmentation, image generation, and other tasks [33–36].

A deep learning-based beam location method was proposed by [24] which uses Garfield [37] and ROOT [38] to generate data.Compared with traditional methods, Ref.[24]provided higher accuracy and better multi-trace location results than conventional algorithms.However, Garfield and ROOT were used to simulate the process of beam injection into the electron collector without requiring the generated images to mimic detailed features, such as the noise distribution and shape of the tracks in the real image.Because the results of neural networks are highly dependent on the quality of the datasets and are sensitive to the detailed features of the data, it is unreasonable to train the networks directly using the data generated by Garfield and ROOT directly.In addition, Ref.[24] does not consider the effects of noise on the final results.In particular, irrelevant noise can easily mislead the judgment of a neural network because of its sensitivity to details.The encoder–decoder structure of the neural network that [24] uses is based on U-Net [39],which is one of the recognized successful methods for image segmentation among the deep learning methods.The encoder–decoder structure and the jump–join approach used in this method can provide surprising segmentation results.In this study, U-Net was used as the comparison method.

3 Methodology

In this section, we provide a specific methodology for generating synthetic data and the FML.

3.1 Noise reduction

We found that the real beam track image contains a large amount of noise.A large amount of noise affects the model’s judgment of real tracks; therefore, we need to preprocess the data for noise reduction.During noise reduction, it is important to maintain the track characteristics.There are many image denoising methods, such as NL-means [40] and DnCNN [41].However, they tend to produce better denoising results by changing the original pixel values.We found that the neural network has a good discrimination ability for a small amount of noise and obvious traces; therefore, it is not necessary to remove the noise completely because it will not improve the accuracy significantly but may destroy the important characteristics of the tracks.By observing real beam traces, we found that a large number of noise points had grayscale values that were much smaller than the grayscale values of the traces.Therefore, we consider noise screening of all pixel points before the track location works by setting a threshold value for grayscale values.By comparing several noise reduction results, we found that the grayscale values of most noise were contained in the latter 99% of the grayscale distribution.Therefore, we sorted the grayscale values of the image pixels, fixed the pixels that are in the top 1% of the grayscale distribution, and set the remaining 99% of the pixel grayscale values to 0.Using this method, we can remove a large amount of noise while maintaining the track characteristics.

3.2 Generation of synthetic data

Training a neural network that works well requires a large amount of data.Thus, it is crucial to generate data that are similar to real data.Based on the characteristics of beam projection data, we designed a method that can generate large quantities of simulation data.For convenience in subsequent experiments, we only describe in detail the method for generating a beam image after noise reduction.The method of generating a beam image before noise reduction is similar and only a few parameters need to be changed.

By observing a real beam image after noise reduction, we found that it had the following distinct features:

(1) A small amount of noise is scattered throughout the image.Most of the noise has small grayscale values,and a small amount of noise has slightly large grayscale values.

(2) The heads and tails of the track are often densely packed with high grayscale points tightly attached to the straight line where the track is located.

(3) The middle part of the track was always composed of loose points with low gray values.The paths consisting of these points were intermittent.

(4) The shapes of the paths were not the same; some were very thin, while others were slightly thicker.In addition, one path was always thick at both ends and thin in the middle.

According to the characteristics of the real track image after denoising, we generated a simulated image according to the following steps.Step 1To achieve the effect of a small amount of random noise with inconsistent gray values on the image,we assigned a valueato each pixel, which was taken from a uniform distribution between 0 and 1.Whena>0.98 , the pixel was marked as a noise point.For these noise points, we assigned each of them the valueb, which was obtained from a uniform distribution between 0 and 1.We set five levels of grayscale values for noise.Whenb<0.3 , we set the minimum grayscale value of level 1; when 0.3 ≤b<0.6 , we set the grayscale value of level 2; and when 0.6 ≤b<0.9 , we set the grayscale value of level 3.When 0.9 ≤b<0.95 , we set the gray value of level 4, and whenb≥0.95 , we set the gray value of level 5.In particular, the highest grayscale value of the noise point was smaller than the average grayscale value of the track area.

Step 2We specified a random integer within 5 for the image, indicating the number of tracks that the image contains.The corresponding number of points in the image was randomly selected as the starting point of the tracks.Because tracks on the same image usually have the same slope, we took a random number from 0.2 to 0.6 as the slope of the tracks of this image.To increase the randomness, we added a ±0.001 deviation to the slope of each track with a 10% probability.We can then obtain the track labels for the simulated data.

Step 3We set three levels for track width thresholds.There is a 45% probability that the tracks will have a fine shape at Level 1; 35% and 20% correspond to Levels 2 and 3, respectively.

Step 4We set three levels for the average grayscale of tracks.For one track, at the head of the track, the average grayscale value was high, whereas in the middle of the track,the average grayscale value was low.At the tail of the track,the average grayscale value oscillated randomly between the two.

Step 5The track had a certain width and was not completely continuous.Therefore, we set the parametercfor the pixels on the track label, which means that this pixel has a probabilitycof not showing the track, indicating that the track is broken here.Clearly, at the head of the track,c=0 ,and in the middle of the track,c=50.

Step 6Depending on whether the pixel shows a track or not and the width threshold of the tracks, we took dense points around the track and chose the number of points randomly within the threshold.

Step 7In accordance with the quality of the real datasets,we added a Gaussian blur effect to the images.

To evaluate the similarity of the synthetic data to the real image, we considered the difference in the gray value distribution and cumulative distribution function of the gray values.If the gray value distribution and the gray value cumulative distribution function of the synthetic and real images are both similar between the synthetic data and the real image, it is reasonable to believe that the algorithm can provide synthetic images that are similar to real track images.Additionally, to avoid chance, we often calculated the average distribution of grayscale for a set of images.In Subsection 4.1, we verify that the synthetic data obtained using the above algorithm are similar to the real data.

3.3 Fast multi‑track location method (FML method)

To conveniently provide the specifics of the FML, Table 1 describes the important symbols.The architecture of the FML method is illustrated in Fig.2.

3.3.1 Data gridding

Because beam tracks are generally straight lines, there is no need to make segmented binary predictions for all pixel points of the entire image, i.e., the location of all pixel points covered by the trace is given in full.In the ideal case of complete accuracy, only two pixel points belonging to the track are required to obtain an accurate location.Considering the length of the effective traces, this study takes eight equal parts in the height direction of the image, i.e.,h=8 , andRow_listwhere each equal part is located is selected.The real column coordinates of each trace in the corresponding row are further obtained using the segmentation labelM.At this time, the column coordinates must be gridded, i.e.,the original width of the imageWis gridded tow, and the column coordinates must be scaled to the original value ofw/Waccordingly, and finally, the single-track training labell∈ℝh×(w+1).By reducing the size of the neural network output shape, the size of the learnable parameters can be effectively reduced.

3.3.2 Predicted points of tracks

We used neural networks to achieve point prediction for the tracks.

First, we obtain the global features of data through the encoder layers.In particular, the encoder layers are a backbone network consisting of multiple two-dimensional convolutional layers with a residual join.The output of the encoder layers is spliced using position encoding to generate the final features.This process can be formalized as follows.

where the features denoted asFE,HE, andWEare the dimensions of the feature map after the encoder layers, andDis the depth of the output channel.

Table 1 Description of symbols

Second, to locate multiple tracks, we introduce a Slot Attention module with reference to [42] to learn the features of each track independently.Specifically, given an upper limit for the number of tracks to be located, a corresponding number of learnable slots were constructed.Slots correspond to tracks individually and redundant slots do not work.Therefore, each Slot gradually learns the information corresponding to a certain track in the representation inputs.The pseudocode of the slot attention algorithm module is given in Table 2.

Third, after the slot attention module, we obtain the final location results, i.e., the output of the network.Because the slots have learned the features of the corresponding traces,we can generate the final predictionsProb∈ℝNQ×h×(w+1)using the decoder layers and the Softmax function.The decoder process can be formalized as:

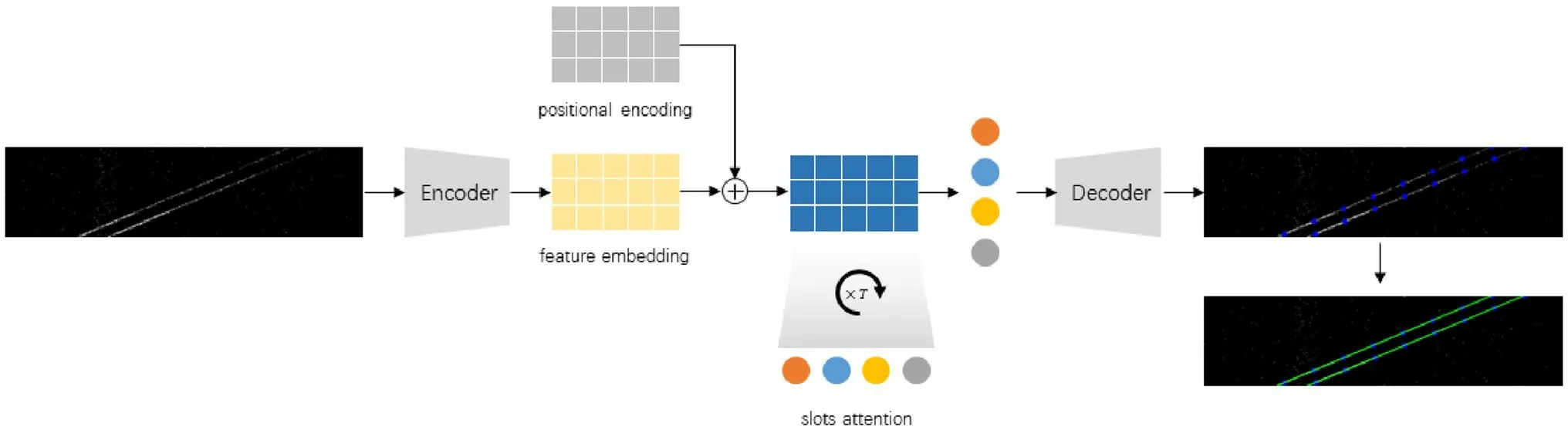
Fig.2 (Color online) Architecture of the FML method

Table 2 Pseudocode of the Slot Attention algorithm module

Because the training label isL′∈ℝNtrack×handNtrack≤NQ,it must be filled withNQ.The missing part is filled withw+1 to indicate the absence of a trace, thus forming the final labelL∈ℝNQ×h×(w+1).Similarly, the dimensionw+1 in Prob is due to the possible absence of tracks at this position.In the training phase, the classification Loss is calculated between Prob andL.Because the pixels belonging to the tracks are only a small part of the entire image, there is a significant imbalance between the positive and negative samples.Therefore, we use Focal Loss (FL) to replace the commonly used cross-entropy loss.

Additionally, because the traces were straight lines, a Straight Loss was constructed for each trace prediction to restrict its performance to straight lines.We calculated the difference between adjacent rows of Prob and found the second parameter as the loss function.

During the testing phase, the weighted sum of Prob and column coordinate values was used as the final predicted position.

3.3.3 Tracks fitting

After obtaining the predicted points for each track, we can fit the final predicted tracks by the coordinates of the predicted points corresponding to each track.Because we want the final fitted tracks to be as close as possible to our predicted points (xpred,ypred) , we use the least-squares method to obtain the final location resultsy∗=kx+b.

4 Experiments and results

In this section, we present the results of preprocessing for noise reduction, a visual and distribution comparison between synthetic and real images, and the comparison results for single-track locations, multiple-track locations,and real track locations.We chose the mass center method,double edge detection method, and U-Net method as the comparison methods for single-track locations, and the double edge detection method as the comparison method for multiple-track locations.

4.1 Denoising and synthesis of data

4.1.1 Data denoising

To improve the accuracy of beam location, we first preprocessed the original data by noise reduction.The original data are presented in Fig.3a, c.It is evident that the original image contains a large amount of conspicuous noise.This noise can affect the model’s judgment of the beam tracks,particularly the method based on the mass center method.Figure 3b, d shows the results of our processing of the original data.A large amount of noise was removed and the tracks remained clear and distinct.It is worth noting that the noise-reduced image retains important features of the track,such as the width and grayscale.

Fig.3 Comparison of data before and after noise reduction.a Original image 1; b image 1 after noise reduction; c original image 2; d image 2 after noise reduction

4.1.2 Data synthesis

By carefully observing the characteristics of the real beam tracks, we generated a large amount of synthetic data.Figure 4 shows our generated synthetic data.Comparing Fig.4 with the real data shown in Fig.3a, c, it is clear that both of them have similar characteristics; for example, the front part of the track has a higher gray value, the middle part of the tracks is intermittent, the front part of the track is thicker than the back end, and so on.Although it appears that the features of the synthetic image are similar to those of the real image, we would like to provide stronger evidence.Because our device is still in the development phase and is limited by the beam time, we selected 337 real images from the beam and calculated the average frequency of each gray value appearing in one real image, as shown by the red histogram in Fig.5a.The red histogram in Fig.5b shows the grayscale’s average distribution of 10000 synthetic images.

The blue curve in Fig.5a, b is the cumulative distribution function of the gray values.It is clear that the distribution of the synthetic data is similar to that of the real data, which provides a strong evidence that the accuracy of neural networks trained with synthetic datasets can be migrated to real datasets.

4.2 Location of single track

Fig.4 Synthetic data.a synthetic data 1; b synthetic data 2; c synthetic data 3; d synthetic data 4

Fig.5 Comparison of the distributions of real data and synthetic data.a Grayscale distribution of real data; b grayscale distribution of synthetic data.(Color figure online)

In this subsection, we choose the mass center method, double edge detection method, and U-Net method as the comparison methods for the FML method, whereas for the mass center method, we first locate the start and end points of the track by manual marking.Figure 6b–e shows the local visualization results of the mass center method, double edge detection method, U-Net method, and FML method, respectively.Figure 6f shows the output of the FML model.The results of the quantitative comparison of the four methods are listed in Table 3, where four aspects (intercept residuals, slope residuals, standard error (SE) [19], and speed)were used to evaluate the performance of the four models.In particular, the speed indicator of the mass center method in Table 3 does not include the manually marked time.To eliminate contingencies, the values in Table 3 were obtained by calculating the average of 2000 results.A comparison of the results is shown in Fig.6, and Table 3 shows that the accuracy of the mass center method is affected by the random noise due to the uneven distribution of the synthetic data.The results of the double edge detection and U-Net methods were susceptible to the inhomogeneity of the track.Our method (FML) exhibits the best performance among all four methods, especially in terms of algorithm speed, which is almost 10 times faster than the traditional methods (five times faster than the deep learning-based method U-Net) and is certainly a great advantage.

4.3 Location of multiple tracks

Because the mass center method and U-Net method fail for the multi-track location task, in this subsection, we choose the double-edge detection method as the comparison model for the FML method.Figure 7a–c shows the synthetic image of multiple tracks and the track location results of the two methods.The neural network output obtained using the FML method is shown in Fig.7d.Similar to the results presented in Table 3, we present the quantitative comparison results of the two methods in Table 4, which are calculated using the average of 2000 results.The visualization results and the comparison of index values show that FML has higher accuracy and higher computation speed than the double edge detection method.

4.4 Location of real tracks

Therefore, it is necessary to verify the validity of the model using real data.Because our neural network was trained on synthetic data, it is also a test of the generated synthetic data.In this subsection, for the location of a real single track,we choose the mass center method, double edge detection method, and U-Net method as the comparison models for the FML method; for the location of multiple tracks, we choose the double edge detection method as the comparison model.Figure 8 shows the single track location results of the four methods on real data from beam, and Fig.9 shows the multiple tracks location results of the two methods on real data from beam.Because there were no ground-truth labels, we could not provide quantitative comparisons of the intercept and slope residuals.The SE results are listed in Table 5 to show the comparison of accuracy, which is the accuracy comparison method in practical application [19].A comparison of the results presented in Fig.9 and Table 5 assertively shows that the FML method can locate multiple tracks well.In particular, we compare the algorithm speeds in Table 5,which is one of the main concerns in this experiment, and we can easily find that the FML method is far superior in speed, which indicates that FML is an efficient online tracking algorithm.

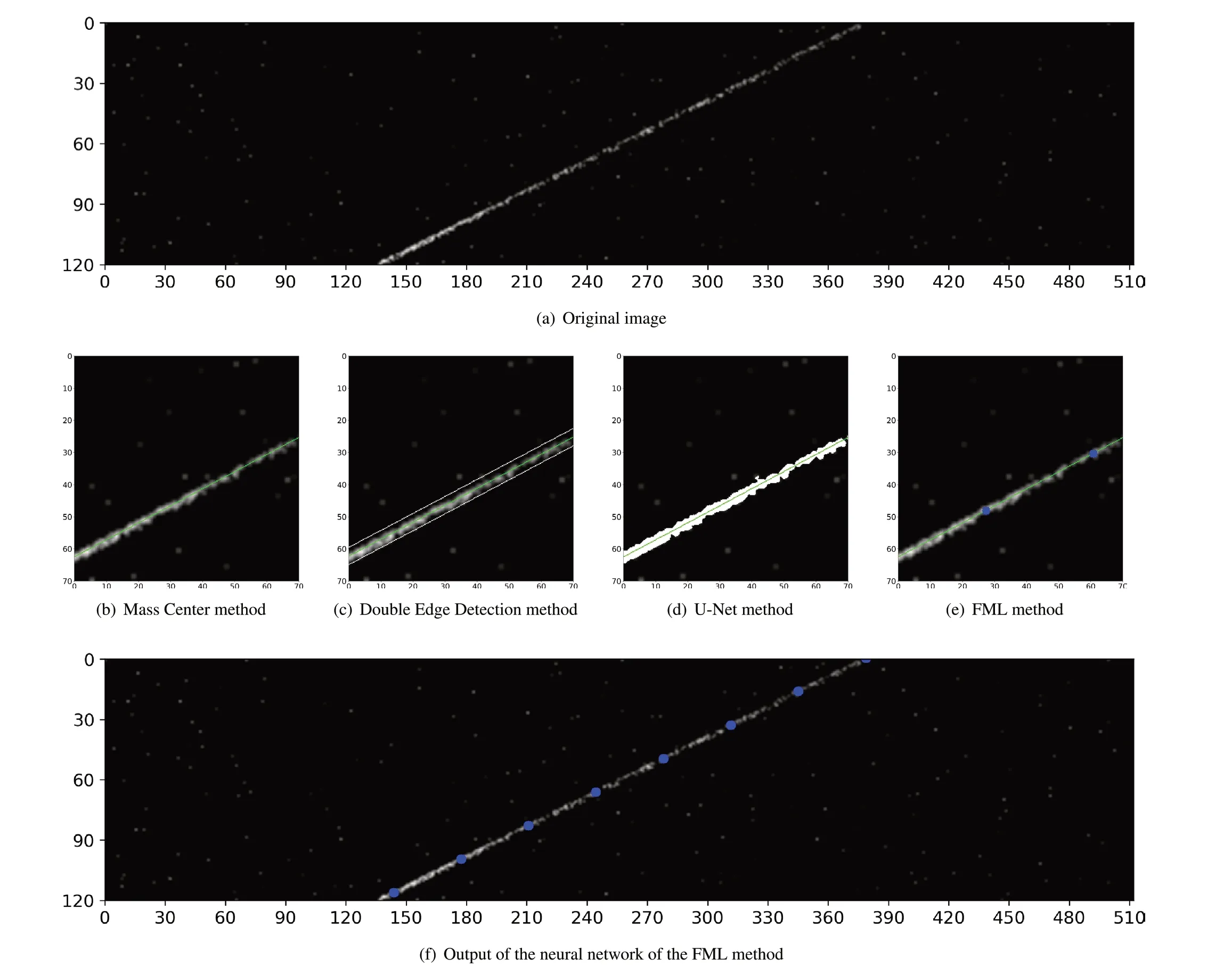
Fig.6 Location of single track.a original image; b mass center method; c double edge detection method; d U-Net method; e FML method; f output of the neural network of the FML method

Table 3 Quantitative comparison of single-track location

Fig.7 Location of multiple tracks.a Original image; b double edge detection method; c FML method; d output of the neural network of the FML method

Table 4 Quantitative comparison of multi-track location

Fig.8 Location of real single track.a Original image; b mass center method; c double edge detection method; d U-Net method; e FML method

5 Conclusion

A non-intercepting and high-resolution beam position monitoring device, called Hi’Beam-SEE, is being designed for HIRFL.The Hi’Beam-SEE consists of a detector system and a readout system.The novel Topmetal-M silicon pixel chip in the detector system directly collects negative ions generated by heavy-ion-ionized air under an electric field, thus producing tracked images.Because of the need to match an event rate (particle flux) of 10 kHz, the system generates a large amount of data that must be processed online.In addition, the projected tracks of the beam are not clear because diffusion occurs during charge drift.Therefore, it is necessary to design an algorithm that simultaneously improves the accuracy and processing speed of positioning on the beam tracks.In this study, we proposed a method called FML based on drifting pixel sensors for fast multi-track locations.To address the limitations of traditional methods, we extracted the global features of the data through the encoder part of neural networks, learned the features of each track independently using the Slot Attention module, and outputted the final location results using a decoder to achieve fast and accurate location of multiple tracks.To make the neural network more accurate and robust on real data, we designed a method to generate synthetic data based on the important features of real data.After verification, the synthetic data had a gray value distribution similar to that of the real data, and the neural network trained by the synthetic data could also provide a highly accurate location for the real data.Comparative experiments demonstrated that the FML method has the lowest bias and fastest speed on a single synthetic track location and multiple synthetic track locations.On real data from the beam, the FML method is valid for multiple tracks and is an efficient online locating algorithm.FML improves the performance by more than five times over the suboptimal algorithm in terms of both processing speed and standard error.In particular, the FML algorithm can operate at a speed of 238 fps.

Fig.9 Location of real multiple tracks.a Original image; b double edge detection method; c FML method; d output of the neural network of the FML method

Table 5 Algorithm comparison on real data

Author ContributionsAll authors contributed to the study conception and design.Material preparation, data collection, and analysis were performed by Yu-Xiao Hu, Cheng-Xin Zhao, and Hai-Bo Yang.The first draft of the manuscript was written by Yu-Xiao Hu, and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data availabilityThe data that support the findings of this study are openly available in Science Data Bank at https://www.doi.org/10.57760/sciencedb.j00186.00064 and http://cstr.cn/31253.11.sciencedb.j00186.00064.

Conflict of interestCheng-Xin Zhao is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article.All authors declare that there are no competing interests.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made.The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material.If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.To view a copy of this licence, visit http:// creat iveco mmons.org/ licen ses/ by/4.0/.