梁弯曲振动的键合空间表示及其在炮口扰动分析中的应用
2023-07-10林圣业王茂森谢杨杨李勇戴劲松
林圣业,王茂森,谢杨杨,李勇,戴劲松
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.西北机电工程研究所,陕西 咸阳 712000)
0 引言
梁的弯曲振动问题一直是学术界和工程界的研究热点。目前,国内外学者已开展了大量关于梁弯曲振动的研究[1-3],分析方法主要包括解析法[4]、有限元法[5]和传递矩阵法[6]等。这些方法各具特色,均已在梁弯曲振动分析中获得广泛应用。但应该看到,以上方法对外接口方式单一,不能很方便地嵌入到多能量范畴耦合的复杂系统动力学模型中。如针对火炮开展连发射击条件下的发射动力学研究时,往往需要联合仿真[7],费效比高。
键合图法[8-10]根据能量守恒,采用统一的方式描述多能量范畴物理量,是解决上述问题行之有效的方法。如惯性元-容性元(IC)混合场键合图法[11]、双功率流键合图法[12]和拉格朗日键合图法[13]等,都在梁弯曲振动分析中获得了成功应用,取得了良好效果。然而,传统的键合图理论将平动和转动视为两个能量范畴的运动,为表征梁弯曲的平动-转动耦合作用,键合图拓扑结构十分复杂,给因果关系的确定带来了困难,不利于发挥键合图法自动符号推导状态方程的独特优势。
本文针对梁发生小挠度弯曲振动的特点,在满足功率守恒的条件下将平动和转动集成到一个能量范畴,构建梁弯曲振动的键合空间表示方法,继而建立梁弯曲振动的键合空间模型,推导系统状态方程,分析自由梁的固有频率特性,以验证梁弯曲振动系统键合空间模型的正确性,再将之嵌入到某火炮自动机发射系统动力学模型中,开展连发射击条件下的炮口扰动分析,通过射击试验验证所提方法的有效性。
1 梁弯曲振动键合空间模型
1.1 梁的键合空间表示
以Timoshenko梁为研究对象,根据质量不变原则和转动惯量不变原则,将梁离散成由N-1个弹簧联接而成的N个集中质量-无质量刚杆组合。定义梁单元的势空间向量、流空间向量、动量空间向量和位变空间向量分别为
(1)
(2)
(3)
(4)

根据功率流和因果关系绘制梁弯曲振动的拓扑结构图,如图1所示。图1中,集中质量表示为共流结1和惯性元件I的组合,刚杆表示为转换器TF,弹簧表示为共势结0和容性元件C的组合。

图1 梁弯曲振动的键合空间拓扑结构图Fig.1 Bond space model for the beam unit
1.2 梁弯曲振动系统状态方程
从图1可以看出,独立的元件为Ii(i=1,2,…,N)和Ci,i+1(i=1,2,…,N-1),其特性方程如下:
1)惯性元件:
(5)

2)容性元件:
(6)


(7)
(8)
l为梁单元等效刚杆的长度,E为弹性模量,IB为惯性矩,ν为剪切系数。
(9)
(10)
式中:Ti为转换模数矩阵,根据几何关系得到第i个集中质量左、右刚杆的模数矩阵分别为
(11)
(12)
2 梁弯曲振动固有频率求解
2.1 固有频率求解方法
令:
(13)
将梁弯曲振动系统的状态方程写成矩阵形式:
(14)
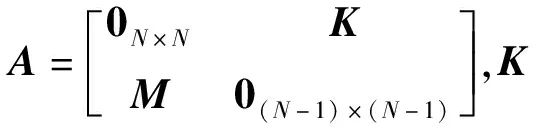
(15)
(16)
式(14)的特征值问题为
λψ=Aψ
(17)
式中:λ为特征值;ψ为特征向量。
按王艾伦等[14]提出的方法求得特征值和相应的特征向量,分别为
(18)
(19)

位移模态的表达式为
ψuξ=diag[(IηSξ)-1]ψpξ
(20)
式中:ξ=1,2,…,β;η=1,2,…,α;Sξ为Laplace算子;α和β分别为独立动量变量和位变变量的个数。
2.2 算例
取一长度为1.2 m的等截面均质自由梁,梁截面为圆环形,圆环外径为50 mm,内径为30 mm,材料密度7 800 kg/m3,材料的弹性模量为204 GPa,泊松比为0.26。由于所研究自由梁是各向同性的,因此仅计算竖直方向的固有频率。为验证所建立的梁弯曲振动键合空间模型,同时采用解析法[15]计算自由梁的固有频率和相应振型:
(21)
Wn(x)=coshsnx+cossnx+vn(sinhsnx+sinsnx)
(22)
式中:ωn为第n阶固有频率,n=1,2,…;Wn(x)为与第n阶固有频率对应的振型;sn和vn为系数,表达式分别为
(23)
(24)
lb为梁的总长度。
采用键合空间法和解析法得到的固有频率列于表1,相应的振型如图2~图7所示。从对比结果可以看出,键合空间法与解析法的计算结果吻合较好,固有频率最大相对误差为0.796 0%,振型相关系数(MAC)不小于0.997 2,说明所建立的梁弯曲振动键合空间模型是正确的。

表1 自由梁前6阶固有频率Table 1 First six natural frequencies of the free beam
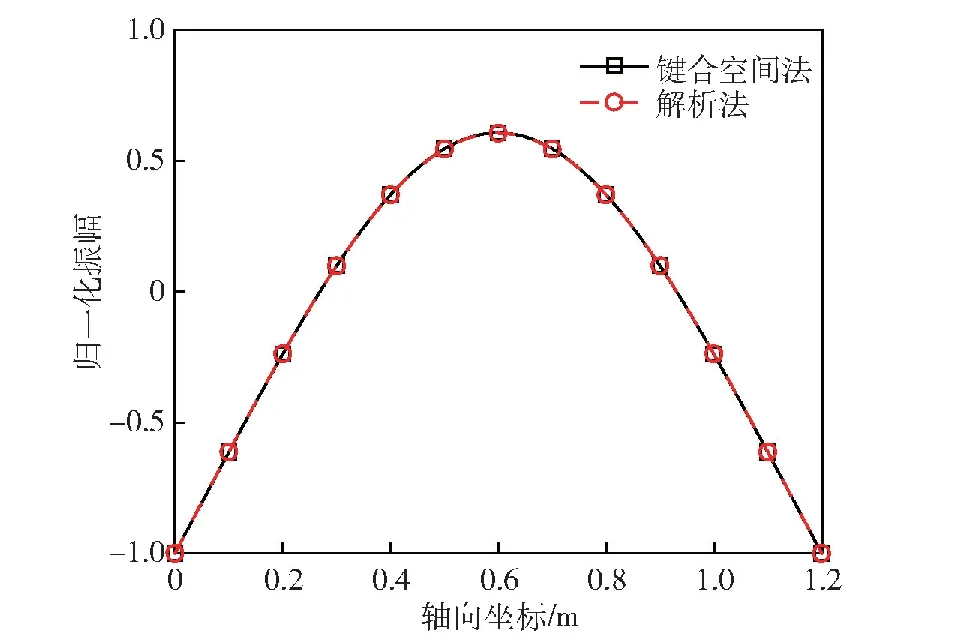
图2 1阶固有振型Fig.2 First-order natural mode of vibration

图3 2阶固有振型Fig.3 Second-order natural mode of vibration
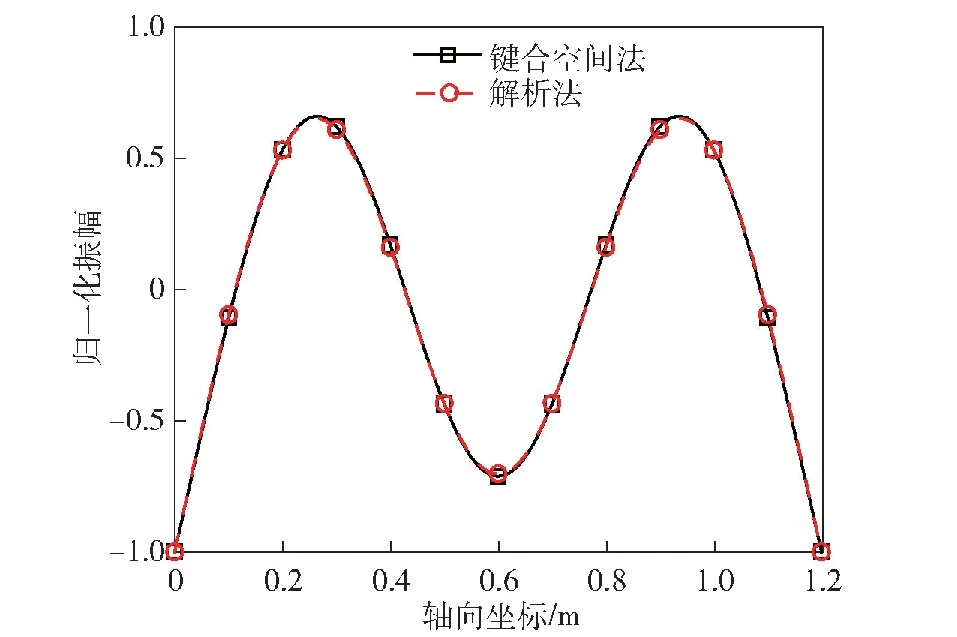
图4 3阶固有振型Fig.4 Third-order natural mode of vibration

图5 4阶固有振型Fig.5 Fourth-order natural mode of vibration
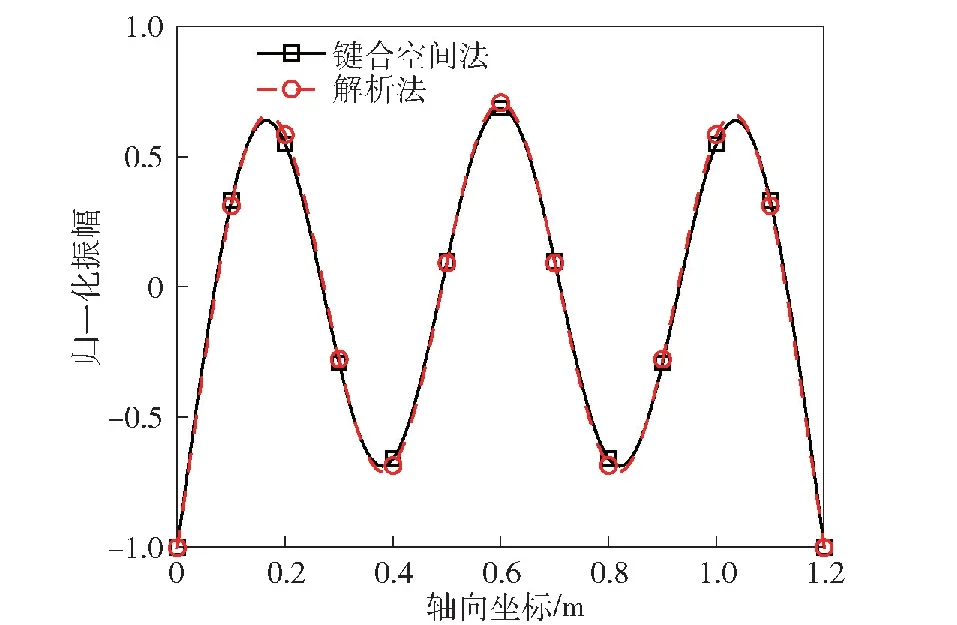
图6 5阶固有振型Fig.6 Fifth-order natural mode of vibration

图7 6阶固有振型Fig.7 Sixth-order natural mode of vibration
3 炮口扰动分析
3.1 发射动力学模型
炮口扰动直接影响射击密集度,一直是火炮发射动力学领域的研究热点[16-21]。将第1节建立的梁弯曲振动键合空间模型嵌入到火炮自动机发射动力学模型中,同时考虑与弹丸的耦合作用,开展炮口扰动分析。
根据某火炮自动机结构特征,将其简化成如图8所示的刚柔耦合模理,继而绘制键合空间拓扑结构图,如图9所示。图9中各结点下标的含义列于表2。

表2 各结点下标的含义Table 2 Description of the subscripts

图8 某火炮自动机物理模型Fig.8 Physical model of the automatic gun

图9 某火炮自动机键合空间模型Fig.9 Bond space model of the automatic gun
从图9可以看出,除了惯性元件I1外,其他所有惯性元件和容性元件都是独立的。推导某火炮自动机系统的状态方程如下:
1)对于炮箱,独立的状态变量包括炮箱与炮管交界处动量p2、后导轨位变q1,r、前导轨位变q1,f。状态方程为
(25)
(26)
(27)
式中:E1为炮膛合力对炮箱质心的作用;C1,f和C1,r分别为炮箱前、后导轨支撑的等效柔度矩阵;n为力指数;R1,f和R1,r分别为炮箱前、后导轨支撑的等效阻尼矩阵。C1,f、C1,r、n、R1,f和R1,r可由L-N接触力模型[22]计算。
2)对于炮管,独立的状态变量包括炮管离散段动量pi(i=3,4,…,N)、相邻炮管离散段交界处相对位变qi,i+1(i=2,3,…,N-1)、炮管上安装缓冲装置处(xi=L)位变qi。状态方程为
(28)
(29)
(30)
式中:Ei、Ci、Ri分别为缓冲装置对炮管离散段作用的等效初力、柔度矩阵和阻尼矩阵;xi为炮管离散段的轴向坐标;L为炮管上与缓冲装置连接处的轴向坐标;lr和lf分别为弹带和前定心部的轴向坐标;Ri,r和Ri,f分别为炮管内壁对弹带和前定心部支撑的等效阻尼矩阵;δ(t)为分段函数,其表达式为
(31)
t为时间。
3)对于弹丸,独立的状态变量包括弹丸动量pN+1、弹带相对各个炮管离散段的位变qi,r(i=2,3,…,N)、前定心部相对各个炮管离散段的位变qi,f(i=2,3,…,N)。状态方程为
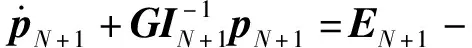
(32)
(33)
(34)
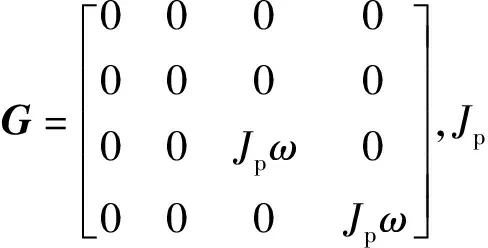
采用4阶龙格-库塔法求解方程组式(25)~式(34),得到火炮连发射击条件下的炮口扰动qN。
3.2 仿真与试验结果对比
将火炮自动机安装于水平固定台架上开展连发射击试验。采用双目立体视觉测试系统测量炮口扰动,测试原理和实景图分别如图10和图11所示。某火炮自动机主要参数列于表3。由内弹道计算得到膛压曲线、弹丸行程和速度曲线分别如图12~图14 所示。计算得到弹带及前定心部与炮管内壁的接触力曲线分别如图15和图16所示。

表3 某火炮自动机主要参数Table 3 Parameters of the automatic gun

图10 炮口扰动测试原理Fig.10 Test principle for measuring the muzzle disturbance

图11 测试实景图Fig.11 Setup for measuring muzzle disturbance

图12 膛底压力-时间曲线Fig.12 Breech pressure

图13 弹丸行程-时间曲线Fig.13 Displacement of the projectile with time
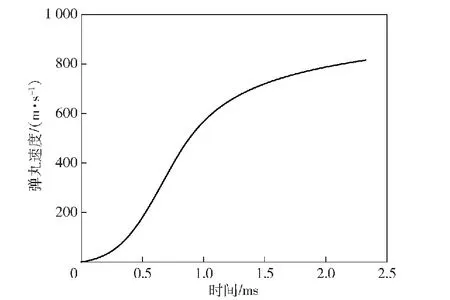
图14 弹丸速度-时间曲线Fig.14 Velocity of the projectile with time

图15 弹带与炮管接触力Fig.15 Contact force between the band and the barrel
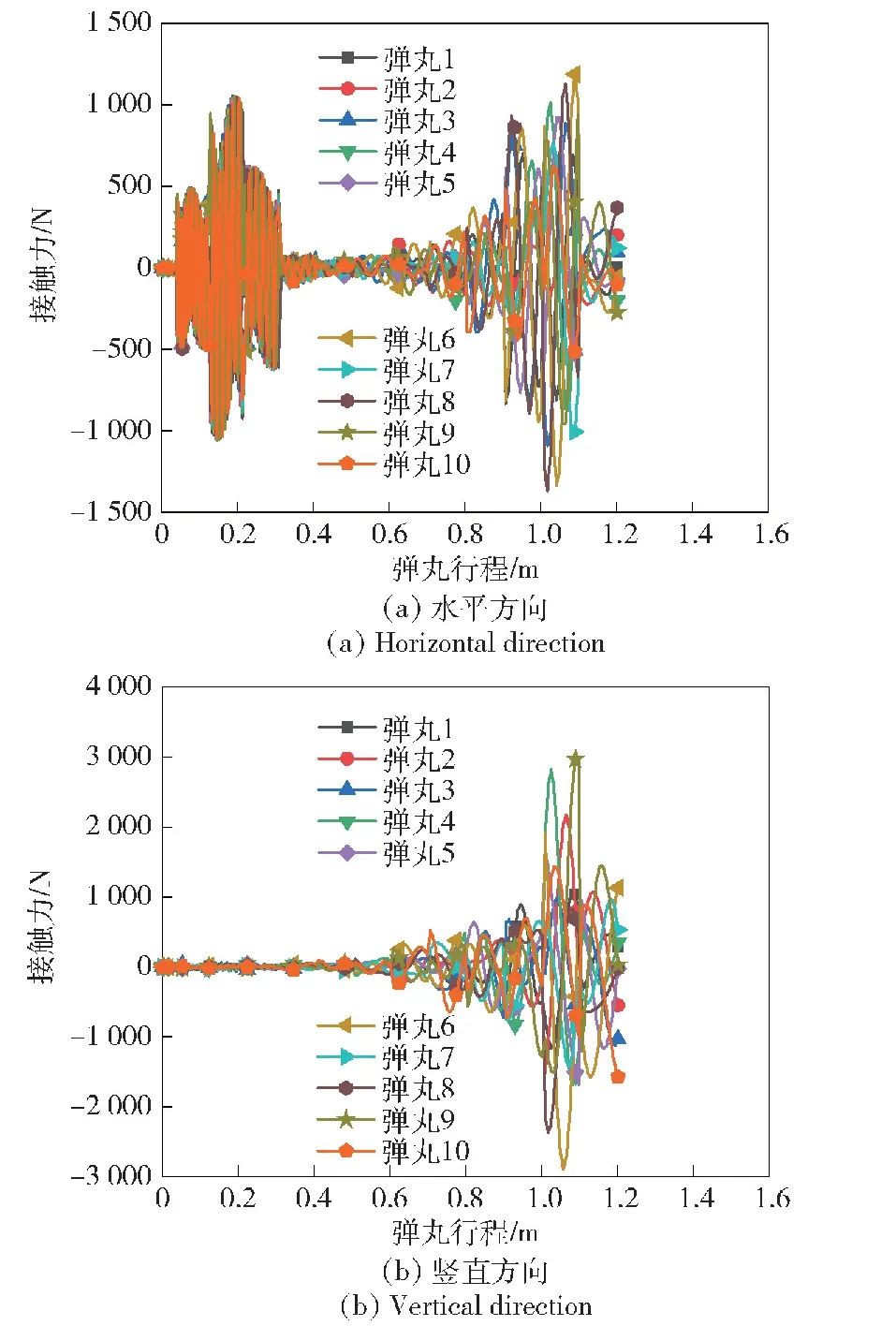
图16 弹丸前定心部与炮管接触力Fig.16 Contact force between the front bourrelet of the projectile and the barrel
采用本文所建模型仿真的垂向炮口扰动与测试数据对比结果如图17所示。从图17中可以看出,仿真与试验结果吻合较好,说明采用本文方法开展炮口扰动分析是可行的。

图17 仿真与试验结果对比Fig.17 Comparison between simulated and experimental results
4 结论
本文构建了梁弯曲振动的键合空间建模和固有频率特性分析方法,结合某火炮自动机具体结构,开展了十连发射击条件下的炮口扰动分析。得出主要结论如下:
1)构建了Timoshenko梁小挠度弯曲振动的键合空间表示方法,相较于传统键合图法,简化了图形的拓扑结构,更易于确定因果关系和符号推导状态方程。
2)提出了梁固有频率特性分析的键合空间法,相较于其他方法,包含动量模态和变形模态,具有更多的模态信息。
3)创建了考虑炮管弯曲变形的火炮自动机系统动力学模型,能够准确计算自动机在连发射击条件下的炮口扰动。
