基于三角函数正交性的永磁伺服系统机械参数辨识

朱其新,姜晨艳,张国平,朱永红

(1.苏州科技大学 机械工程学院,江苏 苏州 215009;2.苏州科技大学 建筑智慧节能江苏省重点实验室,江苏 苏州 215009;3.深圳市大族机器人有限公司,广东 深圳 518058;4.景德镇陶瓷大学 机电工程学院,江西 景德镇 333001)

0 引言

永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)是一种以永磁体进行励磁以实现电能与机械能转换的执行机构,其具有良好的低速性能、快速的动态响应、小的转动惯量和高的转矩电流比,能够很好地满足高性能伺服驱动器的要求,在协作机器人、新能源等领域中得到了广泛的应用[1-2]。在PMSM应用层面不断拓宽的同时,各领域的飞速发展对永磁伺服系统提出了更高的要求,要求其能够在全转速、全转矩范围内控制精确、稳定性好、动态响应快、波动小及对参数不确定据有良好的自适应性等[3],即需要设计优异的速度环控制器和位置环控制器[4]。

为提高控制器的性能,准确获取转动惯量、黏滞摩擦系数、库仑摩擦系数等系统机械参数具有重要意义[5-6]。以工业机器人为例,在运动过程中由于其末端位姿与位置的变化,机器人各轴的负载与转动惯量会发生实时的变化。外在负载扰动的存在将导致机器人各轴伺服系统不能准确匹配,进而导致各轴电机出现振荡、谐振的现象。在永磁同步伺服电机的参数中,电机负载转动惯量的变化对伺服控制系统的机械性能影响最大,当伺服控制系统内部所设置的转动惯量值比实际负载转动惯量大,会降低系统的动态性能与控制精度,相应地若是参数值设置过小,系统响应会加快,但会导致系统速度超调、波动的现象[7]。基于系统数学模型的控制器能够拥有良好性能的前提是机械参数精确,然而在大多数情况下,永磁伺服系统在工作中面临着包括机械参数变化和摩擦在内的多种非线性扰动,控制性能无法得到保证[8-9]。

目前常用的参数辨识算法包括模型参考自适应系统(MRAS)算法、加减速算法、最小二乘算法、扩展卡尔曼滤波算法、状态观测器算法等[10-12]。文献[13]在传统MRAS算法的基础上引入了比例项,同时对MRAS算法的积分项和比例项进行实时更新,进一步提升了算法的自适应能力、参数辨识的精度和速度。传统加减速算法测得的惯性矩值与理论值存在较大误差[14],文献[15]针对变角加速度不恒定且采样信号有噪声的问题,采用积分链微分器随时计算角加速度,同时抑制采样信号噪声,解决了变角加速度引起的大惯性矩识别误测量噪声大等问题。最小二乘算法最初由高斯提出,数据量和计算量大,且以往的数据会对影响新数据的修正效果,因此,在此基础上改进得到带遗忘因子的最小二乘算法、递推最小二乘算法、无偏差最小二乘算法等[16]。卡尔曼滤波算法对模型的依赖性较低,对于速度和负载转矩观测是较好的选择[17],但基于随机模型的卡尔曼滤波器方法的效果并不理想,存在计算负担较重、缺乏必要的设计标准等问题[18]。状态观测器算法可以补偿未知的干扰力矩,并在干扰过程中对机械参数进行辨识,基于状态观测器原理,文献[19]利用扰动观测器估计扰动力矩,并将扰动力矩值应用于惯性矩辨识,性能好但收敛时间较长。文献[20]分别设计了全阶状态观测器和降阶扩展Luenberger观测器,用于估计总负载转矩和转动惯量。

需要指出的是,在众多参数辨识的文献中,鲜有同时考虑辨识电机的转动惯量、黏滞摩擦系数和库仑摩擦系数的,大多数文章在建立数学模型时选择忽略库仑摩擦的影响[21]。文献[22]对电机施加正弦速度指令,利用正弦函数的正交性质,在半周期内进行积分运算分别辨识系统的转动惯量、黏滞摩擦系数和库仑摩擦系数,但此方法只适用于负载转矩为0 N·m的情况。同样,文献[23]利用三角函数的正交性,实现了转动惯量与摩擦系数的解耦,消除了常值负载转矩对机械参数辨识的影响,同时分析了积分区间和参考转速幅值对辨识结果的影响。

本文在文献[22]的基础上,提出一种适用于不定负载转矩工况下的机械参数辨识方法,消除不定负载转矩对辨识结果的影响,利用摩擦系数辨识结果对速度过零处的“爬行”现象做一定的补偿,同时利用摩擦系数和转动惯量辨识值,对不定负载转矩进行观测,经变补偿系数运算后进行前馈以获得更好的实时控制效果。

1 永磁伺服系统数学模型

PMSM是一个高阶、非线性和强耦合的被控对象,存在磁饱和效应、磁滞损耗等,电磁关系复杂,很难进行精确求解,为突出主要问题,需忽略次要因素,故在建立PMSM数学模型时,作出如下假设：

1)定子三相绕组完全对称,在空间中互差120°电角度,所产生的磁场沿气隙按正弦规律分布;

2)永磁体电导率为0 S/m,永磁体内部的磁导率与空气相同;

3)永磁体产生的励磁磁场沿气隙按正弦规律分布;

4)各相绕组中感应电动势波形为正弦波;

5)忽略铁芯饱和;

6)不计磁滞损耗和涡流损耗;

7)转子上没有阻尼绕组,永磁体没有阻尼作用。

永磁伺服系统在dq坐标系下的定子电压方程为

(1)

式中：ud、id、Ld分别为直轴电压、电流和电感;Rs为定子绕组;uq、iq、Lq分别为交轴电压、电流和电感;ωe为电角速度;φf为永磁体磁链。

表贴式PMSM在采用id=0 A的矢量控制时,电机电磁转矩为

Te=1.5pnφfiq

(2)

式中：Te为电磁转矩;pn为极对数。

伺服系统运动方程为

(3)

式中：J为电机和负载折合到电机轴上的转动惯量;ωm为电机机械角速度;B为黏滞摩擦系数;C为库仑摩擦系数;TL为负载转矩。

2 机械参数辨识方法

本文选用正弦速度指令来进行参数辨识。给系统分别施加幅值不同、频率相同的速度指令：

ωm1=A1sinωt

(4)

ωm2=A2sinωt

(5)

式中：A1、A2为两个不同的机械角速度幅值;ω为角频率,两个速度指令的角频率需保持一致。将角速度代入式(3),可得

(6)

(7)

2.1 系统摩擦系数的辨识

为获得与不定负载转矩和系统转动惯量无关的系统摩擦系数的模型表达式,以式(6)为例,两边同乘sinωt,得

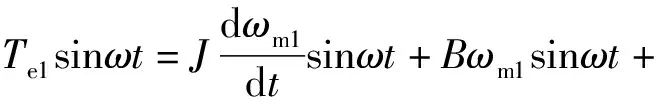
(8)

(9)

式(8)右侧第2项：

(10)

式(8)右侧第3项：

(11)

式(8)右侧第4项：

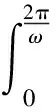
(12)

将式(9)～式(12)代入式(8),得

(13)

同理可得

(14)

解式(13)和式(14)联立的二元一次方程组,得到PMSM的黏滞摩擦系数B、库仑摩擦系数C表达式分别为

(15)

(16)

利用倍角公式和三角函数的正交性,上述推导实现了黏滞摩擦系数和库仑摩擦系数的辨识,同时消除不定负载转矩对辨识结果的影响。

2.2 转动惯量的辨识

为抵消不定负载转矩对转动惯量辨识的影响,在相同的工况下将式(6)与式(7)相减,sgn(ωm1)和sgn(ωm2)显然是相等的,故两式中的sgn(ωm)C项也得以抵消,从而有

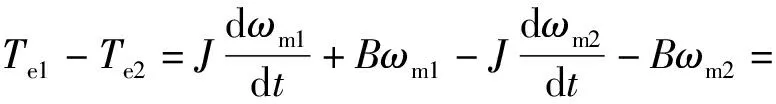
(17)

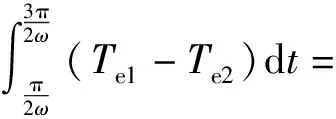
(18)

从而推导出不定负载转矩情况下,PMSM的转动惯量J表达式为

(19)

式(19)推导出的转动惯量仅与电磁转矩有关,不受摩擦系数和负载转矩影响。

本文将机械参数分为系统摩擦系数和转动惯量两部分进行辨识,需要指明推导出的J是电机和负载折合到电机轴上的转动惯量。此外本文提出的辨识方法是在给定速度指令为理想正弦波的情况下推导得来的,但在实际伺服系统中,速度信号由理想正弦信号、离散信号处理系统引起的高频噪声及诸如齿槽转矩的扰动转矩构成,这些噪声和扰动会对辨识结果产生一定的影响,只有当给定的正弦转速信号频率相对较低时,这些噪声对所提方法的影响方可忽略不计。

3 前馈补偿策略

3.1 摩擦转矩前馈补偿

在伺服系统的转速环控制中,速度过零时,受静态摩擦影响,摩擦转矩会出现正负跳变的不连续现象,此时转速环控制器无法快速产生克服此非线性摩擦转矩的电磁转矩,只有当控制器输出的q轴电流产生大于摩擦转矩的电磁转矩时,电机才能实现正常的转速跟踪,伺服系统的控制性能降低。

在辨识出黏滞摩擦系数和库仑摩擦系数后,计算出摩擦转矩并前馈至q轴电流给定,可以帮助控制器产生快速克服摩擦转矩所需的q轴电流,由第2节辨识出的B和C可以推导出摩擦前馈补偿的参考电流值为

(20)

式中：1.5pnφf为转矩常数。

3.2 负载转矩前馈补偿

在PMSM的机械运动方程中,如式(3)所示,选取状态量X=(ωm,TL)T、输入量μ=Te-sgn(ωm)C、输出量y=ωm,则有状态空间表达式

(21)

设观测器增益矩阵L=(L1,L2)T,则有

(22)

从而可得

(23)

(24)

(25)

本文提出的未知恒定负载下基于三角函数正交性的永磁同步电机机械参数辨识及前馈补偿策略的系统控制框图如图1所示。

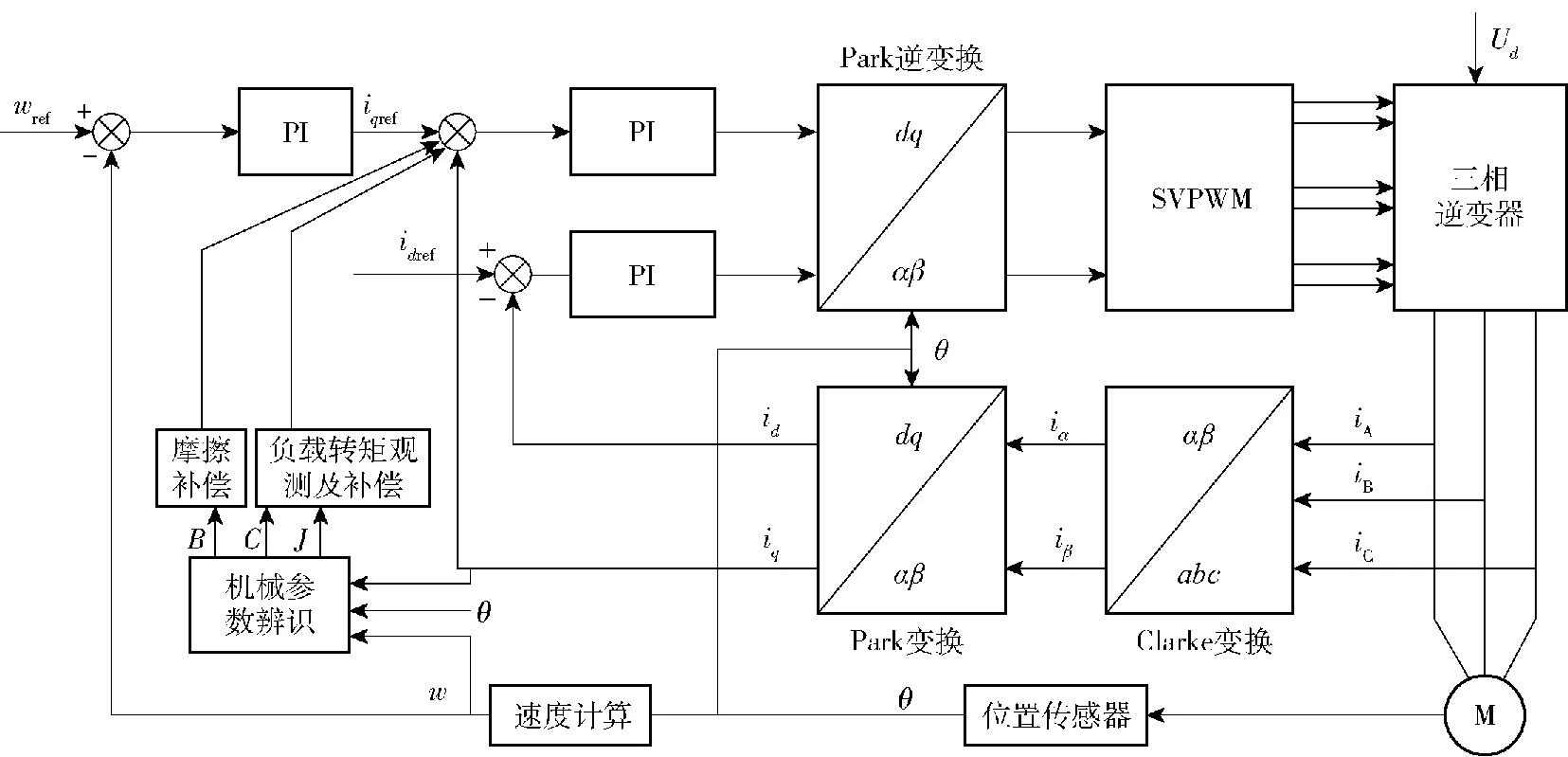
图1 参数辨识及前馈补偿控制框图Fig.1 Control block diagram of parameter identification and feedforward compensation

4 仿真与实验

4.1 仿真

在Simulink软件中搭建如图1所示的系统仿真模型,图中wref和w分别为给定机械角速度指令和实际角速度指令,iqref和idref分别为d轴、q轴的参考电流值,SVPWM为空间矢量脉宽调制环节,iA、iB、iC分别为A、B、C三相的交流电,θ为转子实际位置。仿真中的永磁伺服电机参数设置见表1,给系统施加一个未知恒定负载转矩(仿真中假设其值为5 N·m)。

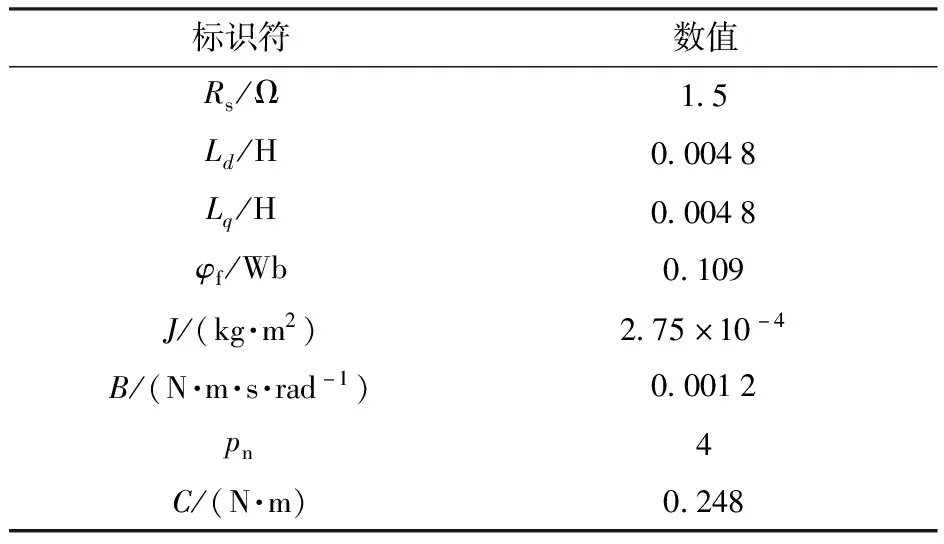
表1 参数设置Table 1 Parameter setting

4.1.1 机械参数辨识

给速度环分别施加机械角速度指令ωm1=20πsin(4πt)和ωm2=60πsin(4πt),即给速度环分别施加转速Nr1=600sin(4πt)和Nr2=1 800·sin(4πt),如图2所示。

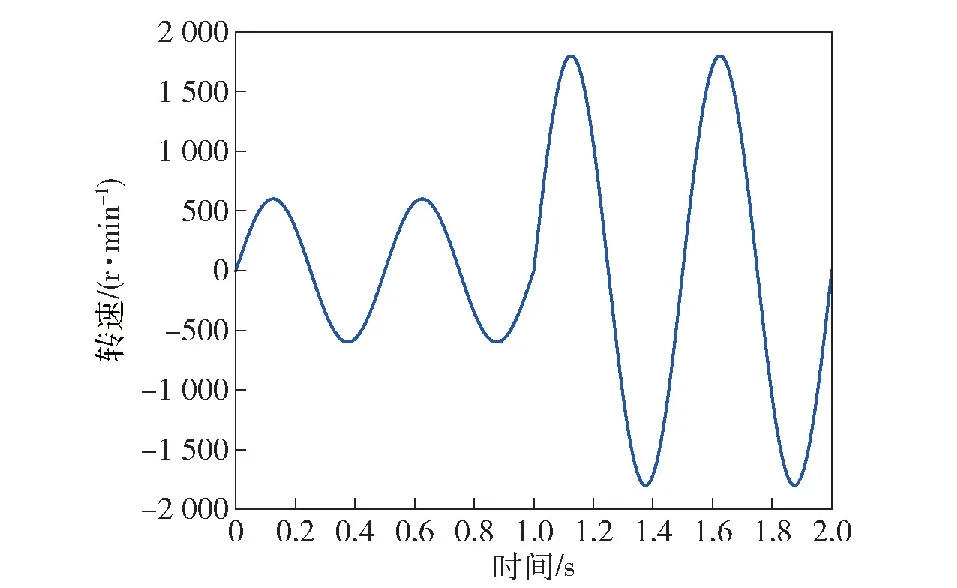
图2 转速指令Fig.2 Speed instruction

按第3节中提出的系统摩擦系数辨识方法,在指定区间内进行积分推导得黏滞摩擦系数B和库仑摩擦系数C,结果如图3所示。

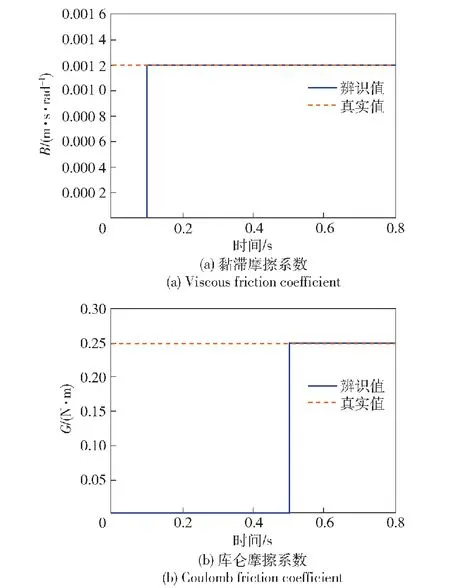
图3 系统摩擦系数辨识Fig.3 Identification of system friction coefficients

转动惯量J数值结果如图4和表2所示。

表2 机械参数辨识结果Table 2 Identification results of mechanical parameters

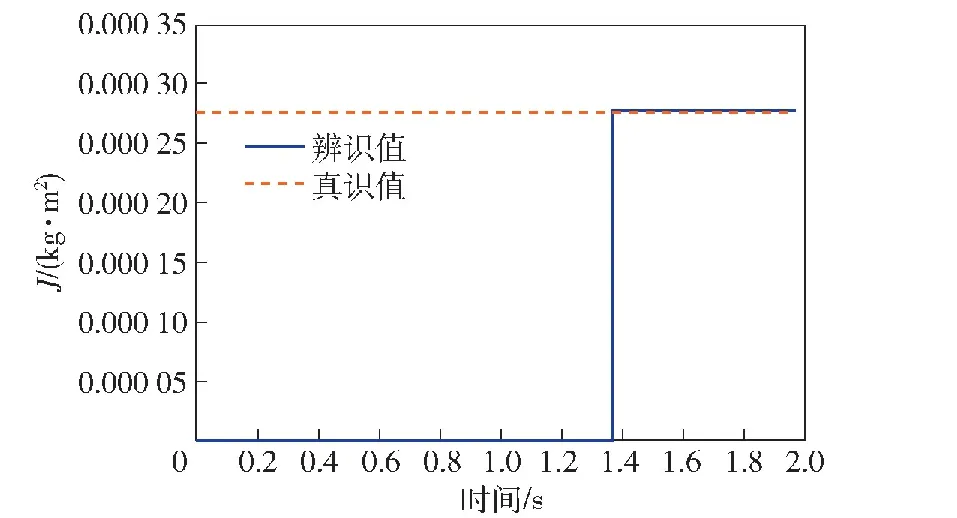
图4 转动惯量辨识Fig.4 Moment of inertia identification

观察表2可以发现,本文所提的辨识方法能够在带未知恒定负载转矩的情况下,有效辨识出电机的机械参数。

4.1.2 前馈补偿

得到各参数的辨识结果后,令PMSM运行于1 800sin(4πt)r/min的给定转速情况下,利用3.2节中的观测器实现不定负载转矩的观测。

图5给出了该工况下的负载转矩观测波形,由图可知,本文设计的观测器可以快速且准确地观测出TL。图6～图9给出了在该工况下的转速误差,其中图6为无前馈补偿的转速误差,图7为有摩擦前馈补偿的转速误差,图8为有负载转矩前馈补偿的转速误差,图9为有摩擦前馈补偿和负载前馈补偿的转速误差。

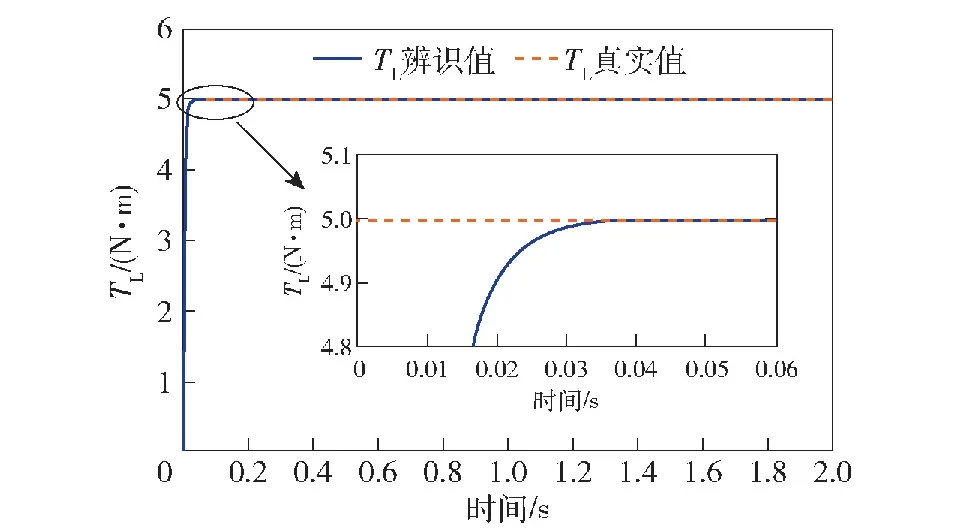
图5 负载转矩观测Fig.5 Load torque observation

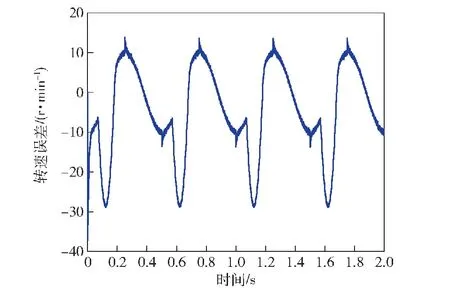
图6 无前馈补偿的转速误差Fig.6 Speed error without feedforward compensation

图7 有摩擦前馈补偿的转速误差Fig.7 Speed error with friction feedforward compensation

图8 有负载转矩前馈补偿的转速误差Fig.8 Speed error with load torque feedforward compensation

观察图6可知：当转速指令过零时,受系统摩擦转矩影响,转速误差为14 r/min,转速跟踪性能降低;受未知恒定负载转矩影响,速度响应有一定程度的滞后。当有产生快速克服摩擦转矩所需的q轴电流后,对比图6和图7可以发现速度过零处的转速误差由14 r/min减小为10 r/min,转速跟踪性能得到改善。将观测到的负载转矩估计值作为q轴电流的前馈补偿(见图8),对比图6和图8发现,实现负载转矩前馈补偿后,响应时间由0.02 s减少到 0.01 s,速度环可以快速跟踪指令转速,负载转矩变化引起的转速误差由25 r/min减小到10 r/min,转速波动得到抑制。最后对比图6和图9可以发现,在得到摩擦前馈补偿和不定负载前馈补偿后,系统的控制性能明显得到了提升。

4.2 实验

为进一步验证本文所提辨识算法的有效性,进行了实物实验。选用深圳市泰金智能有限公司生产功率400 W的60D-A40130D6M永磁同步电机、深圳市大族电机科技有限公司生产的ST5_S_4_220Vac驱动器和明纬(广州)电子有限公司生产的LRS_50_24开关电源,如图10所示。电机的具体参数如表3所示。

表3 电机参数Table 3 Parameter of the motor

图10 实验平台Fig.10 Experimental platform

转矩常数Kt与电磁转矩Te的关系为

Te=Kt×iq

(26)

4.2.1 机械参数辨识

由于实验条件有限,无法在带恒定负载转矩情况下进行实验,因此本文实验在空载情况下进行。实验中给定的正弦转速幅值分别为950 r/min和1 500 r/min,角频率为4π rad/s。为排除采样数据因素对实验结果的影响,采集8组数据进行辨识,结果如图11所示。

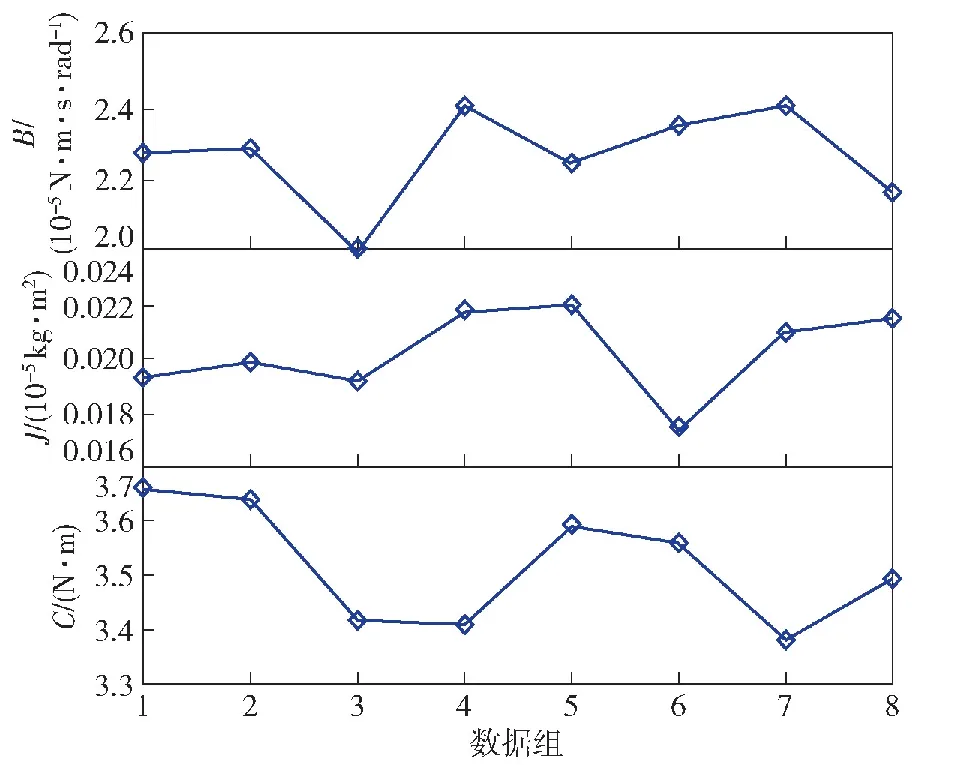
图11 辨识实验结果Fig.11 Experimental identification results

通过观察可以发现,黏滞摩擦系数的辨识值在2.3×10-5N·m·s/rad上下波动,库仑摩擦系数的辨识值在0.02 N·m上下波动,转动惯量的辨识值在0.35×10-4kg·m2上下波动,辨识结果相对稳定。取8次辨识结果的平均值作为辨识结果,从而得出黏滞摩擦系数为2.270 6×10-5N·m·s/rad、库仑摩擦系数为 0.020 4 N·m、转动惯量的值为0.352 3×10-4kg·m2,转动惯量辨识值与标定值误差为3.62%。将摩擦系数用于前馈补偿,如式(20)所示,以解决零速附近转速误差较大的问题。若速度误差减小则证明辨识得到的摩擦系数基本准确,前馈补偿有效。

4.2.2 前馈补偿

实验中施加幅值为1 500 r/min、角频率为4π的正弦参考转速指令,图12为采集到的波形,自上而下分别为q轴电流、实际转速和转速误差。

图12 摩擦补偿前的波形Fig.12 Speed error without feedforward compensation

观察转速误差波形可以发现,在零速附近误差最大,约为50 r/min,这主要是受摩擦的强非线性影响,PI控制器无法快速跟踪上转矩的变化。将实验辨识出的系统摩擦系数代入式(20),给电流施加一个前馈补偿值,补偿后采集到的波形如图13所示。

图13 摩擦补偿后的波形Fig.13 Speed error with feedforward compensation

对比摩擦补偿前后的转速误差波形可以发现,在加入摩擦补偿后,补偿后电流在零速附近产生的电磁转矩有效克服了非线性的摩擦转矩,最大转速误差由50 r/min降低到约25 r/min。由此可知,辨识实验得到的黏滞摩擦系数和库仑摩擦系数准确度较高,产生的摩擦前馈补偿有效提高了转速跟踪性能。

5 结论

本文充分利用了三角函数的正交性,以PMSM的机械运动方程为基准,在带不定负载转矩的情况下,通过施加两个幅值不同、频率相同的机械正弦角速度指令,实现负载转矩与转动惯量、系统摩擦系数的解耦。通过推导出的公式辨识得到系统的机械参数后,利用辨识得到的机械参数值对未知负载转矩搭建观测器进行观测。得到负载转矩值后,通过前馈控制策略,补偿非线性摩擦和不定负载转矩对系统控制性能产生的负面影响。仿真和实验结果表明本文提出的机械参数辨识方法适用范围广、辨识结果精度高,可应用于空载和不定负载转矩的工况下。仿真和实验结果表明了本文所提方法的有效性。