0Cr18Ni9Ti-U71Mn摩擦副高速重载磨损行为的数值模拟
2023-07-10王焕焕林乃明王振霞王玮华曾群锋
严 凯, 王焕焕, 林乃明*, 王振霞, 王玮华, 曾群锋
(1.太原理工大学 材料科学与工程学院, 山西 太原 030024;2.中航工业航宇救生装备有限公司 航空防护救生技术航空科技重点实验室, 湖北 襄阳 441003;3.西安交通大学 机械工程学院, 陕西 西安 710049)
高精尖装备在诸如极端工况(强冲击振动、高速重载等)、极端参数(超大功率/能量、极大/极小尺寸等)和极端环境(高低温剧变、高热流以及强腐蚀等)下服役时,关键零部件的高可靠性和长寿命服役性一直都是机械装备运维领域关注的重点[1].火箭橇是在专用轨道上利用火箭发动机作动力推动火箭滑车高速前进以获取试验测试数据的动态试验装备[2].相较于试验速度可达2 926.6 m/s的美国霍洛曼高速测试滑轨(The holloman high speed test track, HH-STT),我国火箭橇试验速度仅在1 020.9 m/s左右,突破速度瓶颈是当前亟待解决的问题.相关研究表明,火箭橇滑块作为火箭橇与滑轨衔接的重要桥梁,是调控火箭橇试验速度和承载能力的主要零部件材料[3-4].国内普遍使用的滑块和滑轨分别为0Cr18Ni9Ti和U71Mn,然而高速重载下(图1中滑块受力示意图),滑块和滑轨会发生剧烈摩擦,以致于产生大量摩擦热加剧滑块磨损,制约火箭橇速度的提升,并严重威胁试验安全性[5].因此,开展高速重载条件下火箭橇滑块干摩擦磨损行为的研究,提出磨损控制技术,对于保障相关重大装备高效和安全运行具有重要意义.
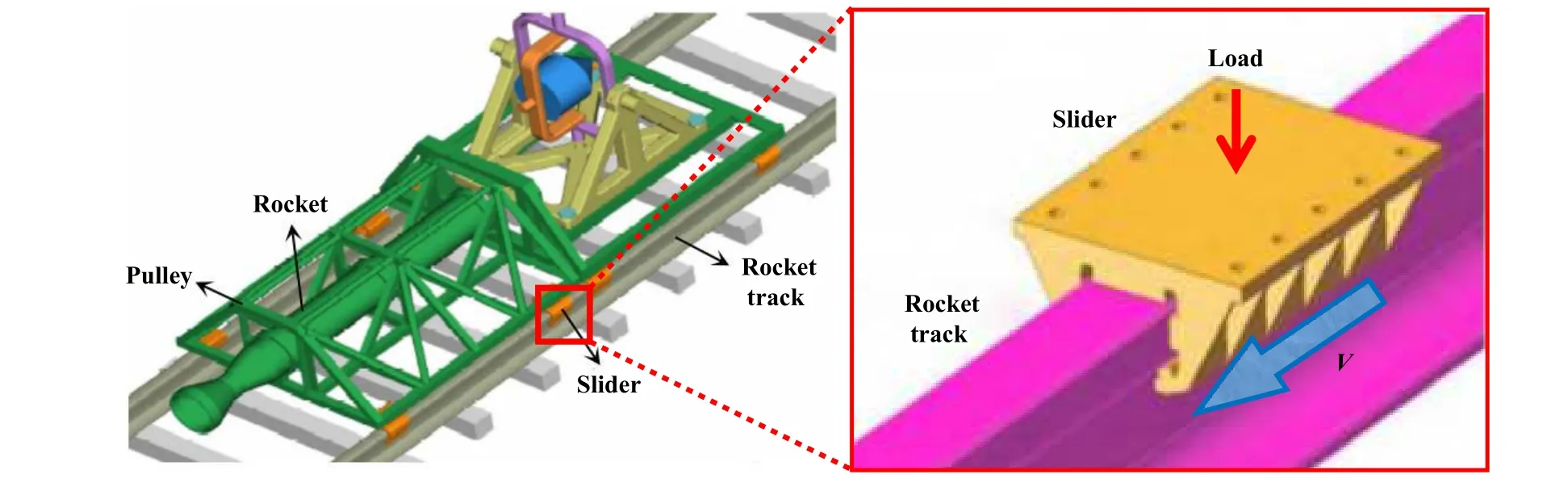
Fig.1 Diagram of rocket sled and force diagram of slide block[5]图1 火箭橇以及滑块受力示意图[5]
传统的评估火箭橇滑块干摩擦磨损分析主要是实测试验手段.Gerasimov等[4]发现高速滑动后滑块的弹性模量和硬度等材料力学性能下降,且出现严重塑性变形和磨损面材料的烧蚀.王玮华等[5]以火箭橇试验后的0Cr18Ni9Ti不锈钢滑块为研究对象,对滑块磨损后的微观形貌和磨损产物进行分析,结果表明滑块表面发生了磨粒磨损、黏着磨损和氧化磨损,滑块材料软化严重,耐磨性下降.汪笑鹤等[6]以试验后的铜合金滑块为研究对象,发现材料硬度沿纵截面2.5 mm范围内由表及里呈现下降变化,且滑块磨损形式为磨粒磨损和黏着磨损.
实测试验固然是最直观且可靠的手段,但火箭橇试验样本量少、试验考核难,因此欲借实测试验手段全方位地揭示滑块磨损行为及磨损动态演变过程是极其困难的,但随着计算机技术和仿真技术的成熟,数值模拟方式成为分析材料摩擦磨损行为的有效途径,并受到广泛关注[7-9].卢铜钢等[10]通过Archard磨损模型分析了温度对枢轨间磨损的影响,发现枢轨间磨损深度随温度的升高而增大.Abood[11]利用Ansys软件研究了接触面粗糙程度、作用力和接触面形状对磨损深度和接触压力的影响,发现粗糙度和作用力对磨损深度或接触压力都有积极影响,而接触面形状会影响接触压力的分布进而促使不同区域磨损深度发生变化.基于Ansys,Rajesh等[12]建立了金属基复合材料的Archard磨损模型,模拟和试验结果均表明载荷和滑移距离对材料磨损率的影响更显著.
火箭橇滑块和滑轨组成的直线导轨作为关键的支撑和引导运动零部件,滑块接触区域所输出的磨损深度以及接触压力等磨损行为对服役生产有很大的影响,但基于模拟手段对滑块磨损行为及磨损动态演变过程鲜有研究.为此,本文中以国内火箭橇普遍采用的0Cr18Ni9Ti不锈钢滑块和U71Mn钢轨钢滑轨为研究对象,构建干摩擦条件下材料的磨损模型,首先进行预模拟分析确定了最大时间子步(Maximum time step,MTS)、磨损时间等参数以及网格划分,其次基于优化了的参数和网格划分进行高速重载磨损模拟,最后从滑块磨损深度和接触压力角度厘清速度和载荷对磨损行为的影响.
1 计算理论与模型建立
1.1 Archard磨损模型理论
Archard磨损模型广泛适用于黏着磨损、磨料磨损以及疲劳磨损等各类磨损环境,许多情况下通过该模型模拟的磨损分布与试验观察结果相吻合[13-14],因此Archard磨损模型可以用于高速重载下滑块磨损过程的刻画.该模型通用形式如下所示:
式中:V和s分别为磨损体积(m3)和滑动距离(m);FN和H分别为载荷(N)和接触对中较软材料的硬度;K为无量纲磨损系数.假设在接触面积ΔA(m2)内,dt时间(s)增量下磨损深度(m)为dh,此时dV=ΔA·dh,以n代表接触压力Pc对磨损率的影响指数,则式(1)变为[15]
研究表明,滑动速度对磨损也有一定的影响[16-17],因此在Ansys中以m代表速度v对磨损率的影响指数[18],进而根据式(2)可以推导出:
若将整个磨损过程离散为N个载荷步,每个载荷步又离散为若干个时间子步.图2所示为离散化磨损过程中载荷步和MTS的关系,其中每个MTS都会进行迭代收敛计算(即完成力和位移的收敛判断).
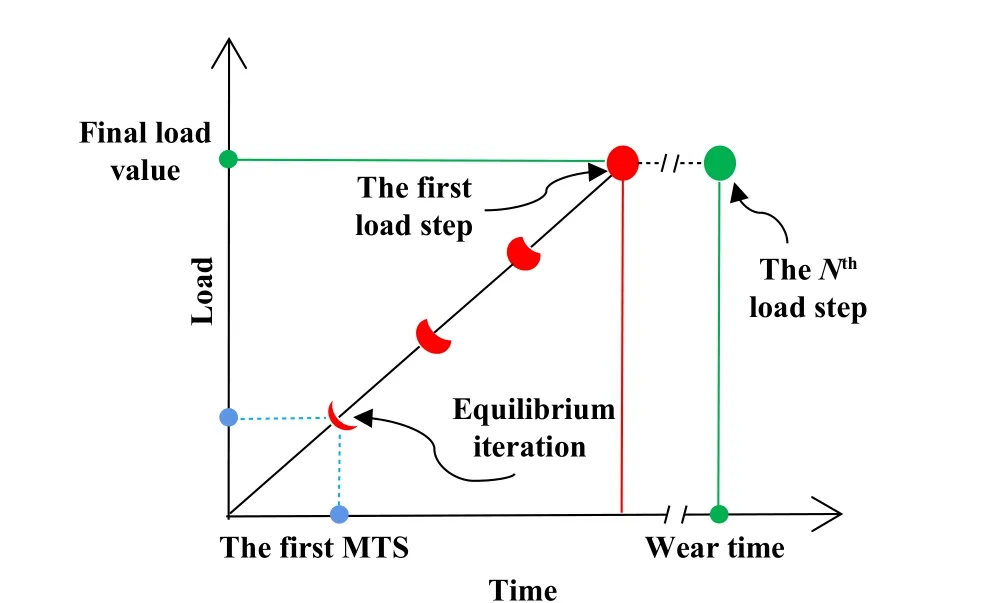
Fig.2 Schematic diagram of load step and MTS图2 载荷步和MTS示意图
那么当速度一定时,离散化单元的第i个节点位置在第j次磨损(即tj时刻)时的磨损深度为
磨损后导致节点位置发生改变,故某节点沿磨损深度的变化表现为该节点沿垂直于滑移方向的磨损深度变化.整个磨损仿真模拟过程如图3所示.

Fig.3 Flow chart of wear simulation图3 磨损仿真模拟流程图
1.2 弹塑性变形理论
0Cr18Ni9Ti材料所受到的应力未达到屈服强度值(220 MPa)就会发生塑性变形[19],且高载荷下考虑材料的弹塑性变形是必要的[20],故本文中引入弹塑性变形理论进行模拟.双线性等向强化模型作为一种典型的弹塑性材料模型,在金属材料塑性加工和高速碰撞等力学响应问题分析方面应用广泛,尤其是在有限元分析中常常通过定义切线模量为弹性模量的1/10或1/20对材料的弹性行为和塑性行为加以分析[21].本文中取滑块材料切线模量为其弹性模量的1/20.
1.3 有限元模型
研究发现高速重载工况下0Cr18Ni9Ti滑块磨损面至纵向1.6 mm范围内力学性能会出现波动[5],综合考虑模拟计算量和模型网格量,兼顾模型简化和吻合实际,采用Ansys workbench中Design modeler模块建立了干摩擦滑动三维几何模型.模型中以0Cr18Ni9Ti不锈钢为滑块材料,建模厚度约为1.6 mm的两倍,即尺寸为11 mm×7 mm×3 mm,而滑轨材料U71Mn钢轨钢不作为主要研究对象,厚度与滑块一致,并设置约束条件和接触摩擦系数0.3[22],如图4所示.材料力学性能参数列于表1中[23-24].

表1 材料的力学性能Table 1 Mechanical properties of material

Fig.4 3D model and constraint settings图4 三维模型及约束设置
1.4 磨损系数K值
已有研究表明[25],0Cr18Ni9Ti-GCr15摩擦副在载荷10 N、转速224 r/min、旋转半径10 mm下磨损30 min后,0Cr18Ni9Ti的磨损率为4.85×10-6mm3/(N·m),根据公式(1)可计算磨损系数为9.365×10-6.
相较于0Cr18Ni9Ti-GCr15摩擦副中两种材料的硬度差,0Cr18Ni9Ti-U71Mn摩擦副中两种材料的硬度差更低,故相同摩擦参数下0Cr18Ni9Ti-U71Mn摩擦副应比0Cr18Ni9Ti-GCr15摩擦副具有更少的体积磨损[26],以致于根据文献[25]所计算出的磨损系数K值偏大.然而,一方面由于该值吻合了K在10-5~10-7的普遍取值范围[27],另一方面是在高速重载条件下火箭橇滑块材料不可避免的会发生较大的磨损,因此可近似认为0Cr18Ni9Ti-U71Mn摩擦副的K值为9.365×10-6.
2 数值模拟与模拟分析
2.1 预模拟
Ansys有限元磨损分析中H以MPa为单位进行输入需要注意,由文献[25]知0Cr18Ni9Ti硬度为197 HV0.2,故取H≈1931 MPa.网格划分是几何结构离散化的唯一途经,是有限元分析中重要的前处理步骤.图5所示为网格划分示意图,获得730 385个节点和148 022个网格.本研究中滑块与滑轨的接触区域是磨损的主要区域,为了更加准确地模拟磨损过程,对该区域的网格进行了加密处理,图4(d)所示为该区域的网格划分,其网格质量为0.941,而接近该区域的网格划分如图4(b)所示,网格质量为0.975.网格质量越好,越有利于模拟过程中准确收集该区域的磨损信息,结果越精确.
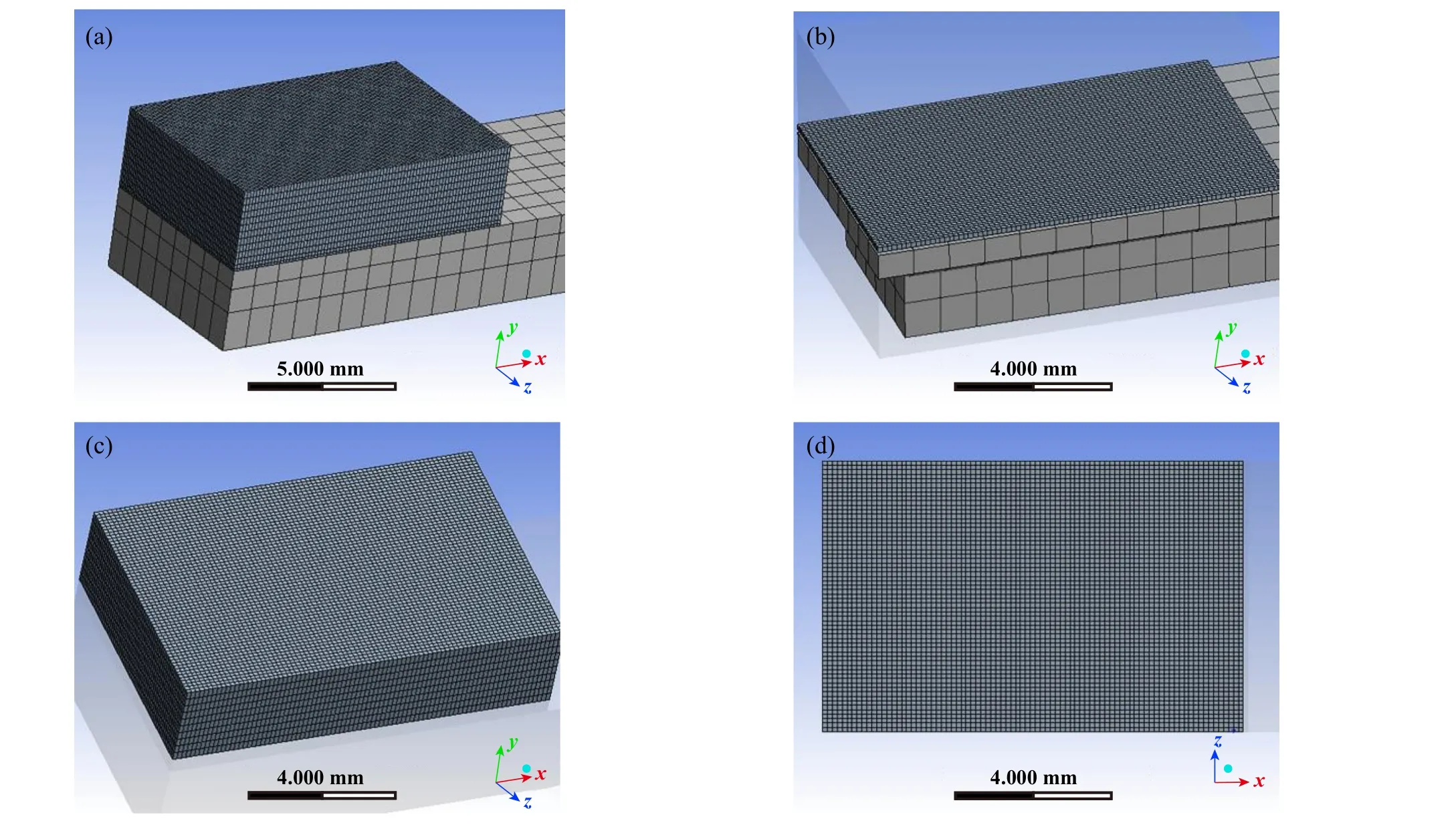
Fig.5 Finite element mesh generation: (a) the overall mesh; (b) the mesh near the contact area of the slider and the mesh in part of the track; (c) the mesh far from the contact area of the slider; (d) the mesh in the contact area of the slider and the track图5 有限元网格划分:(a)整体网格;(b)滑块靠近接触区域的网格以及滑轨部分区域网格;(c)滑块远离接触区域的网格;(d)滑块与滑轨相接触区域的网格
磨损时间从0 ms开始计算,并设置MTS为0.002 ms,预模拟了承载1 kN的滑块以340 m/s在滑轨上运行4.0 ms的磨损状况.图6所示为预模拟获得的接触压力-时间关系曲线.由图6可知,0~1.0 ms内接触压力剧烈变化,在1.0 ms时最大接触压力趋于收敛为27.5 MPa,之后在1.0~4.0 ms内以微弱的起伏变化逐渐下降.这归因于模拟计算初始会传递较大的力以及滑移距离的变化,导致接触压力仅仅在短时间内就有较大的波动,此后滑块底部不断磨损且接触面积增大,受到更大的反向载荷支撑,接触压力反而减小[28].

Fig.6 Variation curve of contact pressure图6 接触压力的变化曲线
与接触压力变化相关的是磨损体积的变化,图7所示为滑块在滑动过程中磨损体积的变化曲线,该曲线表现出了典型的计算体积损失变化,其斜率可以给出体积磨损率.尽管磨损体积不大,但仔细观察可以看到一些细微的特征,即0~0.5 ms内曲线出现了振荡,这是由于对滑块施加瞬间的载荷而产生的惯性效应引起的,一旦滑块中的载荷传递稳定时,体积磨损率就会稳定,并显示平滑的变化.

Fig.7 Variation curve of wear volume图7 磨损体积的变化曲线
0~0.5 ms内的体积磨损率约为1.66×10-3mm3/ms,而在1.0~4.0 ms内,约为1.64×10-3mm3/ms,表明初始惯性效应会引起较大的磨损率,这与接触压力的剧烈变化是密不可分的,反映了高速下滑块磨损深度在极短的时间内就发生了改变.
整个磨损过程中力以及位移的迭代收敛情况如图8所示,发现每个载荷步都实现了收敛(图中虚线为载荷步收敛位置,1个载荷步为1.0 ms),且总共进行了6 029次迭代计算,此外整个磨损过程中位移在第2.0 ms时间内完全实现了收敛(紫色位移收敛值曲线在天蓝色位移标准曲线之下),而力始终处于迭代收敛计算(紫色力收敛值曲线在天蓝色力标准曲线上下浮动).基于前述分析知1.0 ms时间内接触压力变化极其不稳定,至2.0 ms时接触压力以及磨损体积趋于平稳变化,且从图8中可见2.0 ms时(迭代次数3 010次)就显示位移已完全收敛,因此可以认为在3 000次左右迭代计算,即2.0 ms时间内,就已经导致单位时间内增加的磨损体积已经足够小,此后在长时间的稳定磨损阶段对磨损的发展不再构成重大影响.这也进一步表明了以0.002 ms最大时间子步进行计算可以很好的兼顾来自接触力学求解器快速变化的载荷,能够获得具有代表性的磨损结果.

Fig.8 Iterative convergence diagram of force and displacement图8 力和位移的迭代收敛图
2.2 速度及载荷因素模拟分析
预模拟分析结果对模型的修正以及网格优化提供了指导,如图9所示,滑块与滑轨均划分为具有二十节点的可变形的SOLID186固体单元.滑块是主要研究对象,为了提升计算效率且规避因磨损带来的接触面网格变化,相比于预模拟时减少了滑块的网格数量和节点数量,网格数量减少意味着接触面网格尺寸增大,产生的磨损不足以使网格发生较大变化.同时提升了滑块整体的网格质量,处理后,滑块的网格数量为25 500,节点数量少于510 000,网格质量为0.97.

Fig.9 Modelling by Ansys图9 Ansys有限元建模
采用三维非线性面对面“接触对”单元模拟不同时刻两表面间接触面的非线性行为,滑块底部作为接触、滑动以及可变形的面被定义为接触面(CONTA174),而滑轨顶部为可变形的面被定义为目标面(TARGE170).依预模拟结果,模拟时间设置为2.0 ms,MTS为0.002 ms,模拟分析不同速度和不同载荷下的磨损深度数据列于表2中,其余设置与预模拟相同.
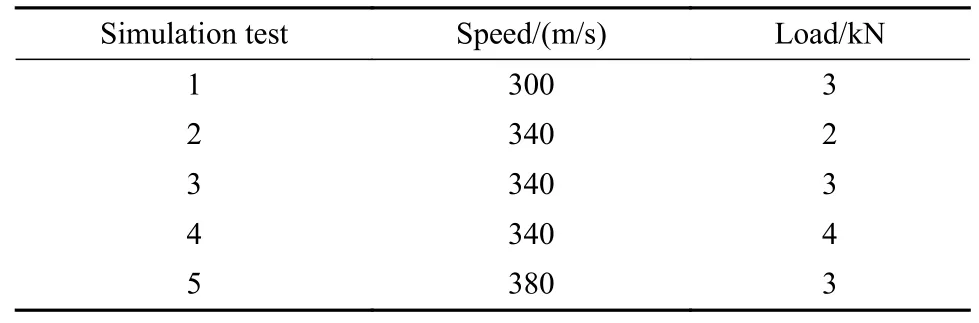
表2 速度和载荷的设置Table 2 Setting of speed and load
2.2.1 恒定340 m/s速度下的摩擦磨损分析
根据表2数据,进行了沿X轴方向、恒定速度340 m/s、载荷分别为2、3和4 kN时的磨损行为模拟.通过自定义CONTA174接触面,可以得到磨损体积随时间的变化曲线,如图10所示.从图10中可知,在2.0 ms时,载荷分别为2、3和4 kN对应的磨损体积为6.6×10-3、9.9×10-3和13.2×10-3mm3,单位时间内的体积磨损率依次为3.3×10-3、4.95×10-3和6.6×10-3mm3/ms.表明随着载荷增大,材料的摩擦磨损会更加严重.

Fig.10 Change of wear volume at constant velocity图10 恒定速度下磨损体积的变化
在1.1中阐述过磨损深度与某一节点磨损深度之间的相关性,因此值得注意的是,Ansys workbench中输出的沿指定方向磨损深度的变化实质上是沿该方向上磨损深度的变化.图11所示为在恒定速度340 m/s、载荷为3 kN以及磨损时间为2.0 ms的条件下滑块接触面分别沿X和Z轴方向的磨损深度,发现滑块沿X以及Z轴方向的磨损深度相比于图12中沿Y轴方向的磨损深度要低4~5个数量级,可见滑块接触面沿Y轴方向的磨损深度是总磨损深度的决定性因素,因此本文中不对沿其他方向磨损深度的变化进行探讨.实际上建模初始改变空间轴的方向,则可以计算出指定方向上的磨损深度.

Fig.11 The wearing depth of the contact surface when the speed was 340 m/s, the load was 3 kN and the wear time was 2.0 ms:(a) along X axis; (b) along Z axis图11 速度为340 m/s、载荷为3 kN和磨损时间为2.0 ms时接触面的磨损深度:(a) 沿X轴方向;(b) 沿Z轴方向
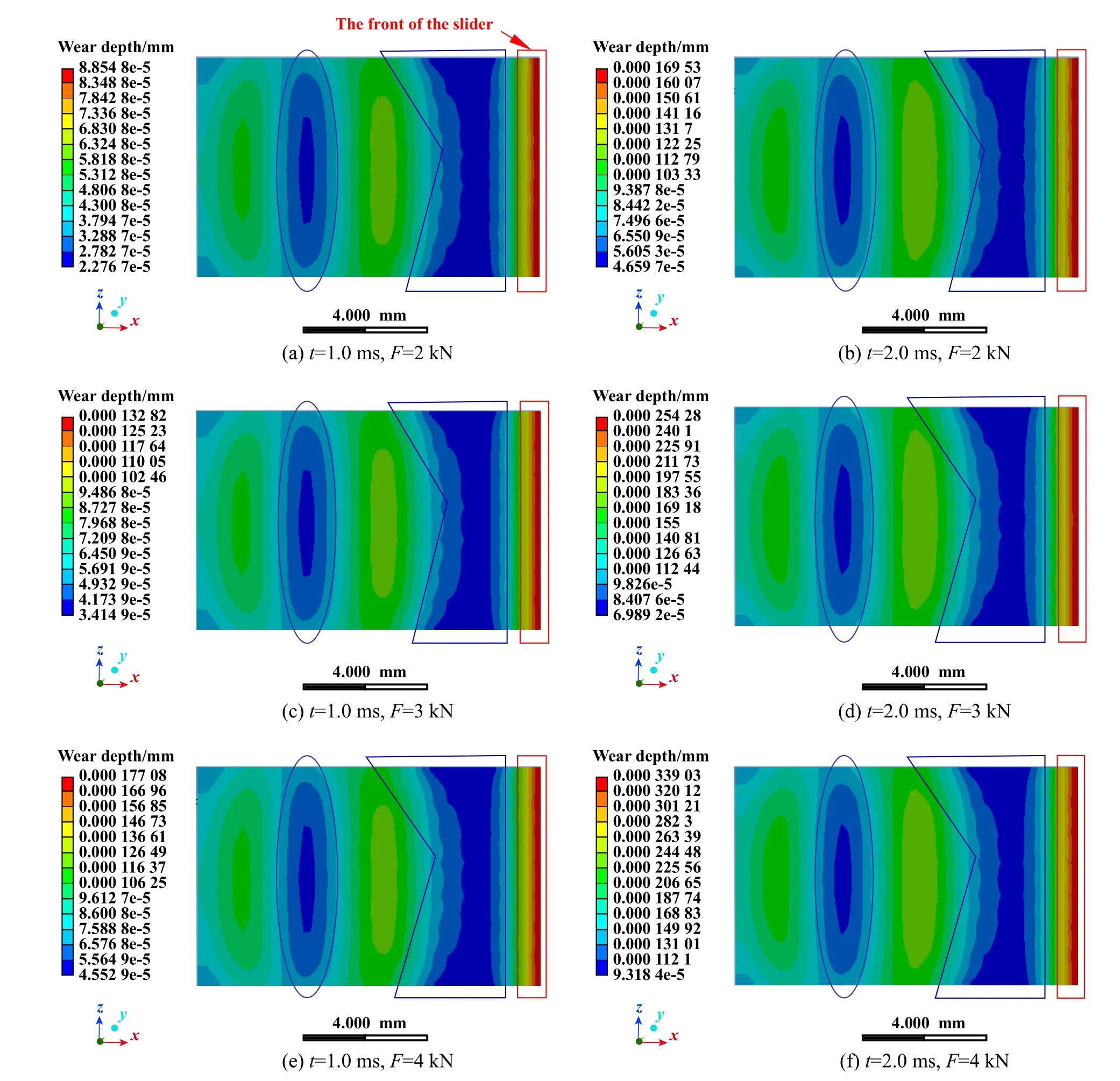
Fig.12 Wearing depth of slider contact surface along Y axis when the velocity was 340 m/s: (a~b) 2 kN; (c~d) 3 kN; (e~f) 4 kN图12 速度为340 m/s时滑块接触面沿Y轴方向的磨损深度:(a~b) 2 kN;(c~d) 3 kN;(e~f) 4 kN
沿Y轴方向的磨损深度如图12所示,比较不同载荷下滑块沿着Y轴方向的磨损深度可以发现,滑块前端始终是磨损最严重的区域(图12中红色方框区域),显然,磨损深度较大的区域之间还存在低磨损深度的区域(图12中蓝色线框区域).从云图变化来看,随着载荷的变化,干滑动过程中磨损深度较大区域未见明显改变,但比较图12(a)、(c)和(e) (t=1.0 ms)可以发现最大磨损深度从8.854 8×10-5增至1.770 8×10-4,最小磨损深度也从2.276 7×10-5微弱增至4.552 9×10-5,同样地在图12(b)、(d)和(f) (t=2.0 ms)中最大磨损深度从1.695 3×10-4增至3.390 3×10-4,最小磨损深度也有所增加,从4.659 7×10-5增至9.318 4×10-5,可见沿Y轴方向的磨损深度随载荷的增加而上升,而2.0 ms时的磨损深度较1.0 ms时增幅不大,故云图无明显变化.
图13所示为速度340 m/s时载荷对接触面平均接触压力影响的等高线图,可以发现,平均接触压力随着载荷的增加而增加,而相同载荷下,平均接触压力随着滑移距离的增加呈现出先增加后减少.由于干摩擦滑动并非理想情况下连续平稳的滑动,故此在模拟中表现为1个物体在另外1个物体表面滑移距离不断增加的断续的滑动过程,易发生振动现象,使得每一时刻接触面与目标面之间的接触状态都是在变化的[29].有限元分析中可以将接触状态分为不完全接触和完全接触[18].因此,在0.5 ms时由于施加瞬间载荷产生了惯性效应导致平均接触压力较低,此后接触压力因载荷传递稳定而增加,但载荷会优先集中到完全接触的区域而形成高压力区,随着滑动持续增加即发生持续性磨损过程,不完全接触的区域就会逐渐变为完全接触,分担高压力区所承受的载荷,就会引起平均接触压力减小[30].

Fig.13 Contour map of the influence of load on the average contact pressure of the contact surface when the velocity is 340 m/s图13 速度为340 m/s时载荷对接触面平均接触压力影响的等高线图
速度为340 m/s时载荷对滑块接触面的接触压力影响如图14所示,从图14(a) (c)和(e) (t=1.0 ms)或图14(b)、(d)和(f) (t=2.0 ms)可以看出,接触面的接触压力均表现出明显的前端效应[31],并与沿Y轴方向磨损深度的变化趋势相同,均是随载荷增大而增大,且高压力区意味着磨损深度较深,低压区意味着磨损深度较浅.另外,根据对比图14(a~b)或图14(c~d)或图14(e~f)可以发现,随着滑移距离的增加,滑块前端的接触压力由均匀性平整演变为断续性集中,这将使得摩擦表面产生大量磨损磨粒,造成三体磨损并形成犁沟,进一步加剧磨损,反映了在高速重载情况下持续性磨损会导致摩擦副最先在前端部位失效.同时低压力区域范围在缩小(图中深蓝色区域),较高压力区域逐渐成为最大接触压力区(图中黑色椭圆区域),且持续性磨损致使接触面积变大导致了最大接触压力随着磨损时间的延长而逐渐降低[28].低压力的边缘区域又会因为磨损增加向高压力区转变,分担载荷在高压力区的集中,即表现为低压力区域缩小[30].
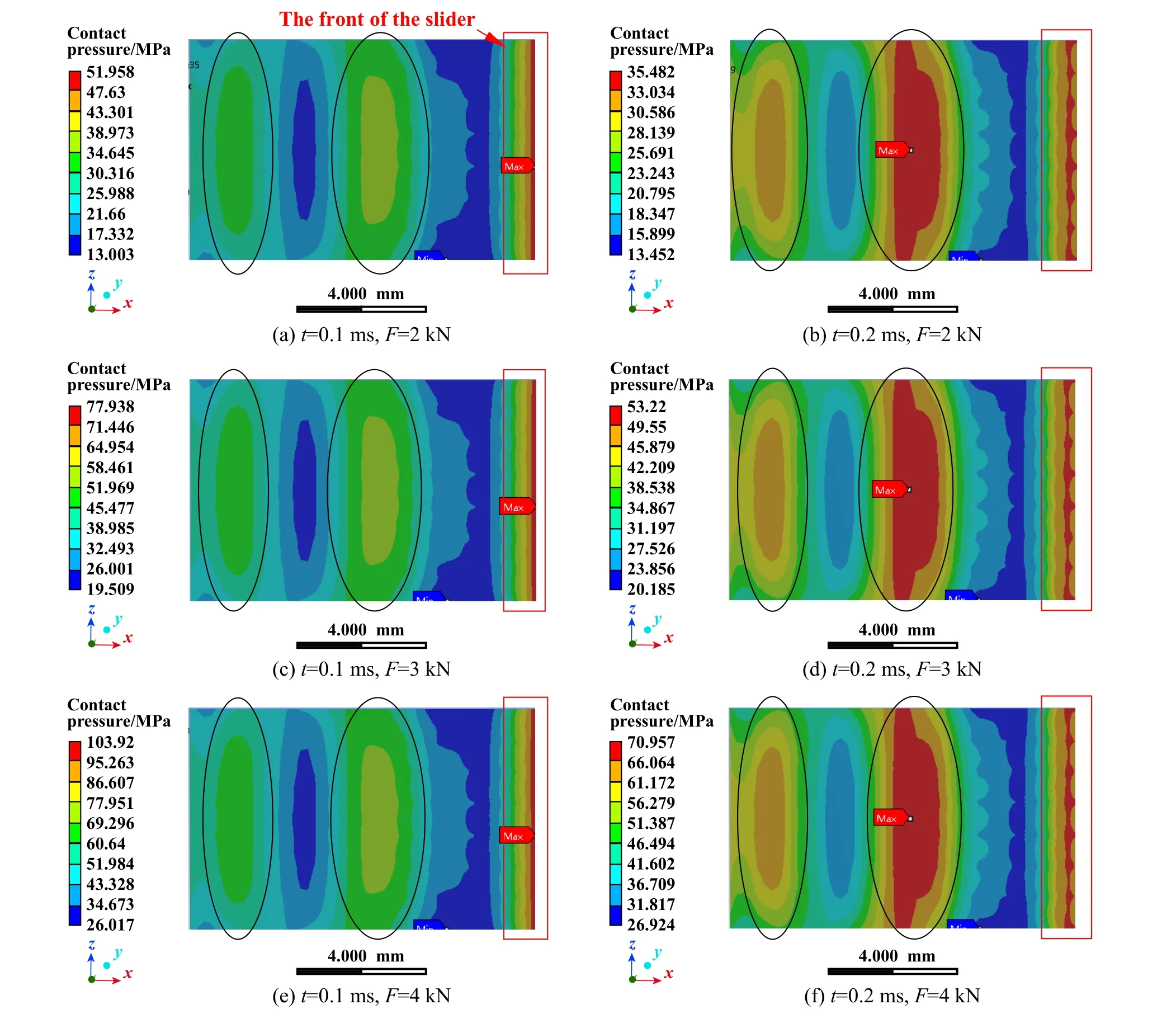
Fig.14 Contact pressure nephogram of slider contact surface when the velocity was 340 m/s: (a~b) 2 kN;(c~d) 3 kN; (e~f) 4 kN图14 速度为340 m/s时滑块接触面的接触压力云图:(a~b) 2 kN;(c~d) 3 kN;(e~f) 4 kN
第1.0 ms内接触压力变化不稳定,因此以第2.0 ms接触压力作分析,即由图14(b)、(d)和(f)可知不同载荷下最大接触压力分别为35、53和71 MPa,即18 MPa/1 kN.工程上依据材料屈服(或局部屈曲)时荷载最大为设计理念[32],那么不考虑应变硬化可认为0Cr18Ni9Ti滑块临界载荷值约为12 kN.
总体来看,由于滑块在高速滑动下有向前下倾的趋势,最大磨损深度区域与最大接触压力区域均位于滑块前端,表现出明显的前端效应,将导致滑块前端较其他区域的磨损更为严重.接触面最大接触压力与最小接触压力之间的差值也在不断减小,这表明随着滑移距离的增加,接触面的磨损将从一开始的局部严重磨损向稳定的磨损转变.
2.2.2 恒定3 kN载荷下的摩擦磨损分析
根据表2中的数据,进行了恒定载荷为3 kN,速度分别为300、340和380 m/s时的磨损行为模拟.同样地,在结果分析中自定义CONTA174接触面,可以得到图15所示的磨损体积随时间的变化曲线.从图15中可以看出,在2 ms时间内,速度为300、340和380 m/s时对应的磨损体积分别为8.7×10-3、9.9×10-3和11.1×10-3mm3,即单位时间内的体积磨损率依次为4.35×10-3、4.95×10-3和5.55×10-3mm3/ms.
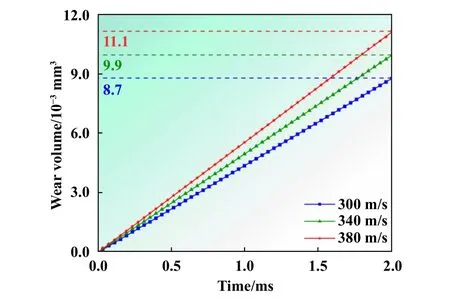
Fig.15 Change of wear volume at constant load图15 恒定载荷下磨损体积的变化
图16所示为在不同速度下t=1.0 ms以及t=2.0 ms时接触面沿Y轴方向的磨损变化云图,由图可知,在恒定载荷以及不同速度下接触面的磨损演变情况.从图16中可以看出,前端效应始终存在,即滑块前端仍然是磨损最严重的区域.

Fig.16 Wear of slider contact surface along Y axis When the load is 3 kN: (a~b) 300 m/s; (c~d) 340 m/s; (e~f) 380 m/s图16 载荷为3 kN时滑块接触面沿Y轴方向的磨损深度:(a~b) 300 m/s;(c~d) 340 m/s;(e~f) 380 m/s
在图12和图14中,恒定速度、不同载荷时前端效应区域几乎没有明显变化,而图16中明显看到恒定载荷时,前端效应区域随着速度的增加而扩大,这是由于单位时间内滑移距离随速度的增加而增加,致使滑块磨损更早进入稳定阶段,而载荷增加不利于磨损阶段的转变.且从图16(a)、(c)和(e) (t=1.0 ms)或图16(b)、(d)和(f) (t=2.0 ms)可以发现,同一时刻下滑块磨损深度随速度的增加而缓慢上升,这主要是单位时间内滑动距离的增加缓慢所导致的.与前端效应区域扩大不同的是,低磨损深度的区域随速度的增加而增加,原因是不完全接触区域因速度增加而增加,降低了接触区域的接触压力,使得接触区域所受摩擦力减小,进而扩大了低磨损深度的区域范围.
载荷3 kN时速度对接触面平均接触压力影响的等高线图如图17所示,可见速度对平均接触压力的影响并不像载荷对平均接触压力的影响一样具有很强的规律性.原因在于随着速度的增加,接触区域的接触状态随滑移距离的增加而不断变化,当接触状态多数处于不完全接触时会导致平均接触压力降低,若多数为完全接触时平均接触压力升高.从变化趋势来看,同一速度下平均接触压力均是呈现出先升后降,速度为300 m/s时上升趋势最明显.此外,对比t=1.5 ms到t=2.0 ms时可以发现,随着速度的增加,平均接触压力的降低趋势明显,缓解了磨损的加剧,这表明增加速度有利于初始磨损阶段向稳定磨损阶段的发展.

Fig.17 Contour map of the influence of velocity on the average contact pressure of the contact surface when the load is 3 kN图17 载荷为3 kN时速度对接触面平均接触压力影响的等高线图
载荷为3 kN时,速度对滑块接触面接触压力的影响如图18所示.由图18(a)、(c)和(e) (即t=1.0 ms时)可见最大接触压力从81.574降至74.344 MPa,同样地在图18(b)、(d)和(f) (即t=2.0 ms时)中可见最大接触压力从63.512降至53.783 MPa,原因在于恒定载荷、速度增加时会引起接触面与目标面之间的振动不稳定,造成实际单位时间内相对运动方向上的接触面积减小,即向不完全接触转变,降低了接触压力.因此在图中表现为低压力区(蓝色区域)随着速度的增加而扩大,而图中标识为蓝色椭圆的低压力区因高速下振动现象的缘故出现向滑块后端偏移的现象.
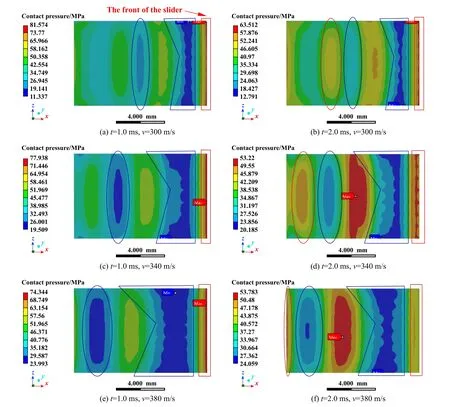
Fig.18 Contact pressure nephogram of slider contact surface when the load is 3 kN: (a~b) 300 m/s;(c~d) 340 m/s; (e~f) 380 m/s图18 载荷为3 kN时滑块接触面的接触压力云图:(a~b) 300 m/s;(c~d) 340 m/s;(e~f) 380 m/s
另外,比较图18(a~b)或图18(c~d)或图18(e~f) (即载荷与速度都一定时)可以看出高压力区范围扩大,低压力区范围缩小,这是由于滑移距离的增加引起接触面发生持续性磨损,致使接触面积不断变大从而引起了最大接触压力减小,最小接触压力略微增加[31].由图17 可以看出平均接触压力并未因高压力区范围的扩大而增加,而是降低的;图18(c~d)则提供了佐证,即最大接触压力的降低程度远远大于最小接触压力的增加程度,平均接触压力降低.
2.3 模拟验证
高速重载动态磨损过程极其复杂,难以满足必要的试验条件,通过试验直接验证本文中的结论将是1个充满困难的任务.在Archard磨损理论受广泛认可的情况下,可以在一定程度上反映本文中磨损结果的正确性,且磨损面的表面形态容易表征,因此本文中主要通过与相关文献中的数据进行比较来验证模拟的准确性.
在图12或图16中均可发现滑块前端、中部以及后端沿Y轴方向的磨损是严重的.第2.0 ms时磨损深度已经稳定,同时考虑到载荷是影响磨损的重要因素,故以340 m/s、载荷4 kN为例[图12(f)],滑块磨损程度:前端(3.390 3×10-4)>中部(2.633 9×10-4)>后端(2.066 5×10-4),这与文献[33]通过对试样厚度测量验证的结果是完全一致的,滑块初始厚度为14.7 mm,经过磨损后其前、中、后部的厚度分别为12.9、14.4和14.5 mm.该结果在文献[34]中也显示出一致性.
另外,在图14或图18中因持续性磨损致使滑块前端的接触压力由均匀性平整演变为断续性集中,这易导致应力集中,使得磨损面产生的磨粒促使犁沟的形成.这与文献[5]通过对试样前端磨损面的微观形貌的分析结果是高度相符的.图19所示为本文中模拟结果与文献中实际结果的对比示意图,可以发现,图19(a)中A'、C'、E'高压力区范围更大,且越靠近滑块最前端时接触压力越集中,甚至出现尖端区域,这将使得A'、C'、E'区域受较长时间的高压力集中作用,导致磨粒出现,而实际结果的分析发现A、C和E区域由于磨粒磨屑的产生导致出现深浅不一的犁沟磨痕或沟槽,这与本文中模拟结果中A'、C'和E'压力集中易导致磨粒产生是相呼应的.同样地可发现,图19(a)中B'、D'高压力区范围小,且沿滑动方向表现为均匀性,这将导致该区域整体受力均匀,不至于产生大量磨粒,这与文献中对B、D区域出现块状磨屑堆积的分析相吻合.

Fig.19 Comparison of the simulation results in this paper and the actual results in Ref [5]: (a) the amplification schematic diagram of the front-end local area in Fig.14(f); (b) SEM micrograph of the microstructure of the local wear surface at the front end of the specimen in Ref [5]图19 本文中模拟结果与文献[5]中实际结果的比较:(a)图14(f)中前端局部区域放大示意图;(b)文献[5]中试样前端局部磨损面微观形貌的SEM照片
Archard磨损模型应用广泛,本文中通过模拟和试验对比发现滑块磨损面模拟结果和试验结果在磨损趋势和表面形貌分析上都呈现出一致性,验证了此模型能够预测局部区域是否存在磨损风险的合理性.
3 结论
利用Ansys有限元模拟软件并嵌入Archard磨损程序代码和定义的弹塑性变形模型,模拟了由0C18Ni9Ti不锈钢滑块材料与U71Mn钢轨钢滑轨材料组成的摩擦副在速度大于300 m/s、载荷大于1 kN时的干摩擦磨损行为,研究了载荷和速度对火箭橇滑块磨损行为的影响.主要结论如下:
a.载荷和速度均是影响滑块磨损深度的主要因素,磨损深度随二者的增加而增大.在本文研究水平范围内,速度对滑块磨损深度的影响并不显著,但速度增加会促进磨损更早进入平稳磨损阶段;相反滑块磨损深度随载荷的增加而显著上升,但载荷增加不利于磨损阶段的改变;此外不考虑应变硬化时滑块的极限承载为12 kN.
b.恒定速度或恒定载荷下的接触压力分布,都存在明显的前端效应,前端出现高应力集中,将使得火箭橇滑块最先在前端区域出现严重磨损,这与相关文献分析是一致的,因此Archard磨损模型能够合理预测局部区域存在磨损风险.
c.数值模拟能够基于火箭橇滑块的服役条件(载荷、速度等)以及火箭橇滑块的力学性能参数计算滑块磨损深度并预测严重磨损区域,这将对解决火箭橇滑块的干摩擦磨损性能、进而提高试验速度的制约等一系列问题提供一定的指导.
d.本仿真模拟过程对接触面粗糙度、材料性能参数与温度相关、摩擦生热等其他因素的考虑不够全面,尚且不能全方位地描述整个磨损过程,但对磨损过程的预测是适用的,可为后续的深入研究提供一种可靠有效的方法.
