基于混合正交法的环喉式膨胀偏流喷管性能影响因素研究①
2023-07-08张渴欣周博成汪根来
王 革,张渴欣,周博成,陈 磊,关 奔*,汪根来
(1.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.中国航天科工集团有限公司第六研究院41所,呼和浩特 010076)
0 引言
火箭发动机是一种可以直接产生推力的喷气推进动力装置,其自带燃料和氧化剂,可以在大气层以外工作,成为宇宙航行和大气层外飞行的主要动力装置。相关研究[1]表明,发动机的性能指标实际上总是低于理论上可达到的值,这是由于在发动机工作过程中,会存在燃料混合、燃烧及燃气膨胀不充分等问题,造成发动机性能损失。在发动机所有损失中,喷管的非适应性损失占据较大比例,最大可达到15%。非适应性损失[2]是指传统喷管在非设计高度工作时,由于喷管内部气流的过膨胀或者欠膨胀而带来的损失,为了减小这种性能损失,多种先进的火箭喷管概念相继出现[3-5],包括双钟型喷管、塞式喷管、膨胀偏流喷管和延伸喷管等,通常将它们称为高度补偿喷管。在这些高度补偿喷管中,膨胀偏流喷管具有长度短、质量轻、型面变化连续等优点,可以削减火箭发动机30%的体积和15%的结构质量[6],因此受到了广泛的关注。
膨胀偏流喷管(ED喷管)的概念由RAO[7]于1960年提出。典型的ED喷管结构包括外壁轮廓和中心塞锥两个部分,这种结构使发动机燃气流经喷管喉部时的方向朝向喷管外壁轮廓,燃气在塞锥拐角处发生膨胀,并在外壁轮廓的限制作用下偏转为喷管轴向喷出。ED喷管存在两种工作模态,即低空开放模态和高空闭合模态。此两种工作模态的转换为ED喷管提供了优秀的高度补偿能力。为了获得ED喷管内更多的流动细节,学者们进行了大量的实验和数值研究[8-14]。研究发现在两种工作模态下,ED喷管内部均存在激波和膨胀波,在“开放”工作模态,超音速核心流经过一系列激波-膨胀波偏转以保证波后压力能够适应大气环境压力;在闭合工作模态,气流在膨胀波束作用下,流动方向发生了较大偏转,超、亚声速区域之间的剪切层与喷管轴线相交,形成再附激波,使气流以平行于轴线方向排出,喷管中激波的位置及强度决定了喷管的流动特性,进而决定了喷管的性能。WANG等[15]数值研究了大扩张比ED喷管内的流动规律,重点分析了推力效率下降的流动机理。SCHOMBERG[16]和TAYLOR[17]等实验对比了ED喷管和传统喷管、双钟型喷管的性能,发现ED喷管的效率要高于传统收敛-扩张型喷管,与双钟型喷管对比后发现,在高压比条件下,ED喷管推力性能更具优势,验证了ED喷管的先进性。同时,学者们也开展了结构参数对喷管性能的影响研究。TAYLOR[18]和SCHOMBERG[19]等研究了喉部几何形状对ED喷管性能的影响,发现ED喷管允许被大幅缩短长度,从而节省结构重量。PARK等[20]研究了不同压比下具有不同塞锥折转角的ED喷管的流动特性,JOHN等[21]数值研究了塞锥基底曲率半径对喷管性能的影响。张琦等[22]采用数值手段,分析了塞锥尾椎角、初始扩张角和收敛角对环喉式膨胀偏流喷管性能的影响,并获得了其最佳值。
本研究拟采用数值手段,对环喉式膨胀偏流喷管(ATEDN)的内流场进行仿真计算,利用混合正交法[23]设计数值模拟实验,探究扩张比、入口压力和塞锥基底半径三个影响因素共同作用下喷管性能的变化规律,为后续ATEDN型面设计提供参考。
1 数值方法
1.1 几何模型及边界条件
ATEDN的计算模型主要由喷管外壁和中心塞锥两部分组成,喷管外壁扩张段母线采用三次样条曲线进行设计,与喉部过渡圆弧保持相切,如图1(a)所示。图中,RH和Re分别为塞锥基底半径和出口半径,Gt为等效喉部宽度,喷管设计直径为30 mm,初始扩张角∠C=53.51°,塞锥下游延伸段长度L=120 mm,其余参数取值参照文献[24]。ATEDN的计算区域如图1(b)所示,喷管入口采用压力入口边界,将远场设置为压力出口边界,喷管壁面为绝热无滑移壁面,考虑本文所使用的ATEDN为二维轴对称结构,因此采用轴对称边界。外部流场沿喷管轴向方向长度设置为20Re,径向长度设置为6Re。
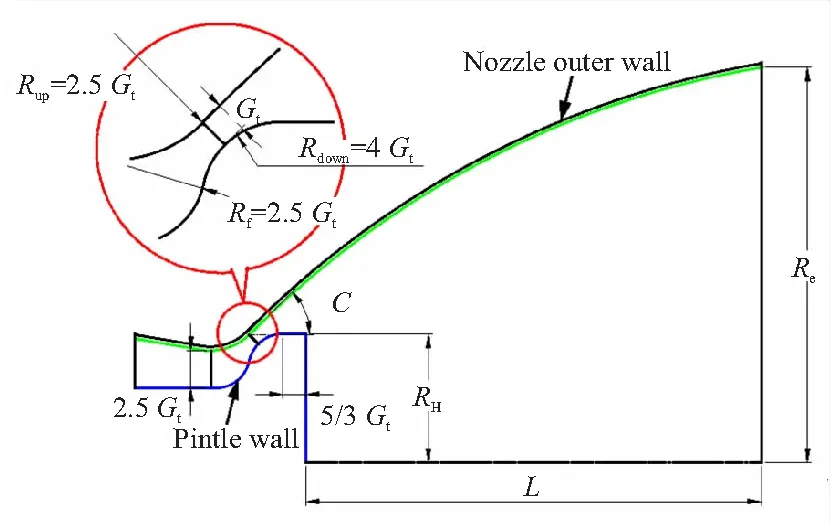
(a)Calculation model for ATEDN
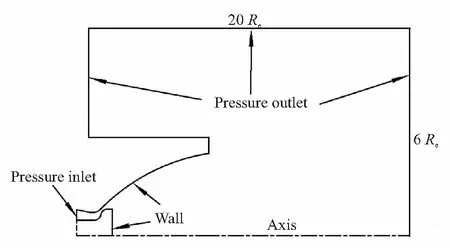
(b)Boundary conditions图1 ATEDN计算模型和边界条件设置示意图Fig.1 Sketch of the calculation model for ATEDN and boundary conditions
1.2 数值模型
针对喷管地面实验工况,不考虑喷管外部高速来流,忽略ATEDN内的化学反应及多相流动,不考虑其内部辐射传热、型面烧蚀等影响,忽略重力的影响,控制方程为可压缩流的N-S方程。
质量守恒方程:
(1)
动量守恒方程:
(2)
能量守恒方程:
(λT)+S
(3)
理想气体状态方程:
p=ρRT
(4)
其中,
Φ=·(τ·v)-(·τ)·v
式中ρ为流体的密度;t为时间;v为速度矢量;p为压强;τ为粘性应力张量;μ为动力黏度;I为单位张量;S为变形速率张量;λ为热导率;T为温度;Φ为耗散函数;R为特定气体常数。
采用剪切应力输运k-ω(SSTk-ω)湍流模型[25]将雷诺平均N-S方程进行封闭,SSTk-ω模型是基于湍流动能k和比耗散率ω的两方程模型,能够较好地预测由于激波引起的分离流动特性[26-27],其表达式如下:
(5)
(6)
式中Gk为由层流速度梯度产生的湍流动能;Gω为ω方程产生的湍流动能;Гk和Гω为k和ω的扩散率;Yk和Yω为扩散产生的湍流。
选取基于密度的隐式求解器求解控制方程,差分格式使用AUSM格式[28],空间离散使用二阶迎风格式。计算在稳态条件下进行,库朗数取值为2,在计算过程中,对喷管出口质量流量进行监控,当残差下降至10-3以下,监控参数无明显变化时,判定计算收敛。
1.2.1 网格无关性验证
采用结构网格对图1(a)所示计算域进行网格划分,并对贴壁网格进行加密处理,网格生成结果如图2所示。在喷管入口压强为4 MPa,出口状态为海平面、压力为101325 Pa的工作条件下,利用40 000、80 000、160 000、260 000网格对ATEDN流动进行数值模拟,绘制不同网格数量情况下的喷管壁面压力变化曲线,如图3所示。可以看出,随着网格数量增加,曲线之间差异逐渐减小,当网格数量达到160 000后,网格数量的继续增加对壁面压力曲线变化几乎不再产生影响,因此本文采用数量为160 000的网格进行数值计算。
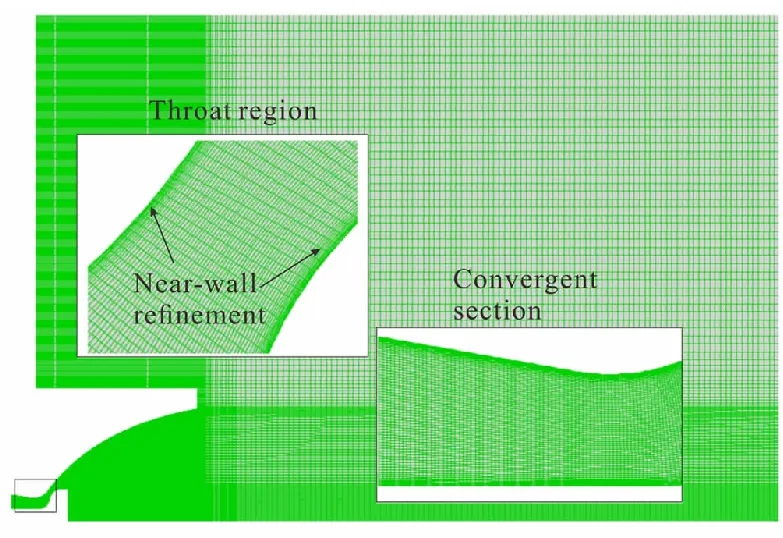
图2 计算区域的网格划分Fig.2 Mesh layout of the computational domain
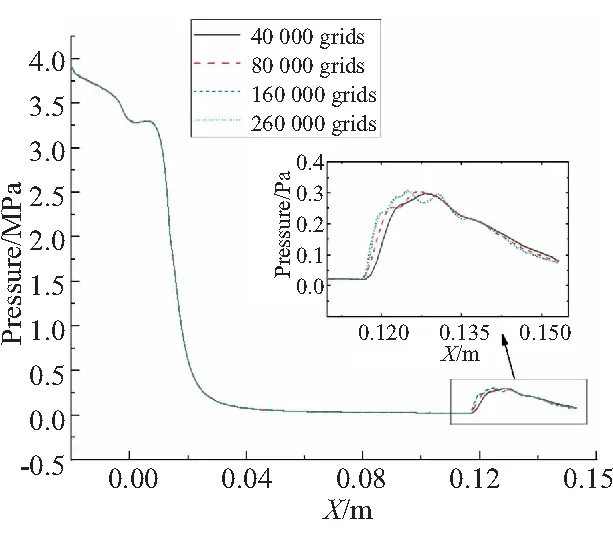
图3 四种不同数量网格下喷管壁面压强分布Fig.3 Pressure distributions along the nozzle shroud with four different mesh layouts
参照WAGNER和SCHLECHTRIEM的实验结果[12]对当前使用的数值方法进行验证,实验与数值模拟图像对比见图4。

(a) Experimental images (b) Numcrical images图4 实验结果[12]与当前数值结果对比Fig.4 Comparison of experimental images[12] with the present numerical results
由图4可以看到,该数值方法可以很好地模拟出WAGNER和SCHLECHTRIEM的实验结果。在该实验条件下,当NPR=10时,喷管流动处于“开放”工作模态,而在NPR=30时,喷管流动处于“闭合”工作模态。数值方法很好地模拟了这两种工作模态下的流动特征,激波和膨胀波清晰,从而证明了数值方法的准确性。
1.2.2 参数设置
喷管工质采用热流燃气,其总温T0=2500 K、比热容比γ=1.161、气体常数Rg=408.35 J/(kg·K)。将燃气视为定压比热容的可压缩理想气体,热导率按动能理论给定,粘性系数按萨瑟兰粘性定律[29]给定。为了分析ATEDN在宽高度下的性能,选取0~31 km之间的8个典型高度工况,不同高度工况对应的大气参数通过《标准大气参数公式》[30]进行计算,计算结果如表1所示。
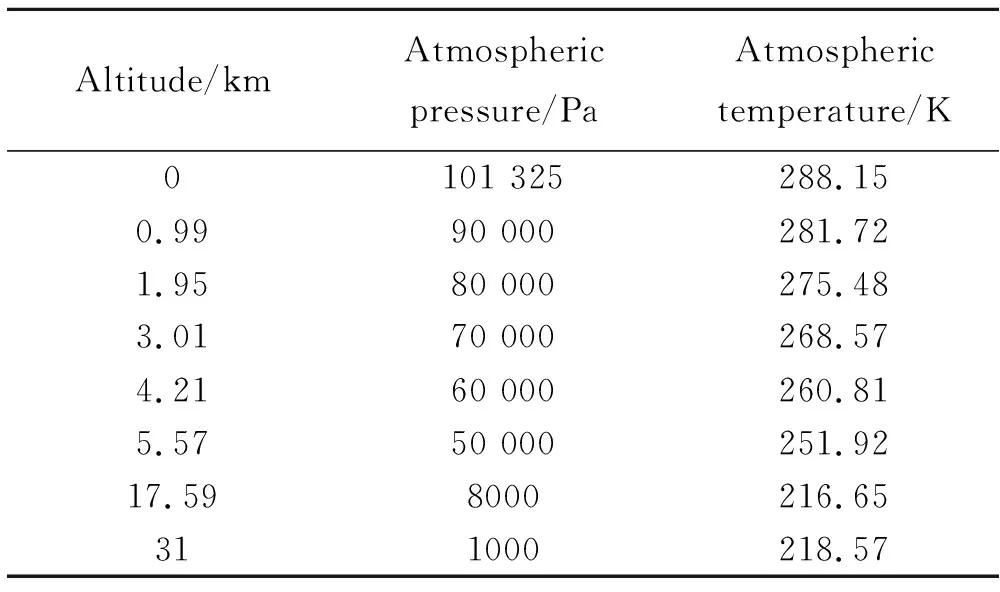
表1 大气参数Table 1 Atmospheric parameters
1.3 喷管推力计算
ATEDN推力为其内、外表面全部作用力的合力,计算公式为
F=Fin+Fex
(7)
其中,Fin由ATEDN入口、喷管外壁面的燃气一侧(图1(a)中绿线)和中心塞锥壁面(图1(a)中蓝线)提供,表示燃气对ATEDN内表面的作用力的合力;Fex由喷管外壁面外侧提供,表示外界大气对ATEDN外表面的作用力。
1.4 混合型正交表设计
现有火箭发动机的燃烧室压强一般都保持在4~10 MPa[31]的水平上,因此选取喷管入口压力的4个水平分别为4、6、8、10 MPa;考虑到ATEDN能够满足大扩张比要求的结构特性[13,22],选取扩张比的4个水平分别为40、60、80、100;而考虑到塞锥基底半径RH过大会降低发动机的有效载荷,在可接受范围内选取塞锥基底半径的3个水平分别为30、34、38 mm。使用上述参数设计用于数值仿真的混合正交表,如表2所示,在之后分析中,将编号1、2、3、…所代表的组合方式称为Case 1、Case 2、Case 3、…。
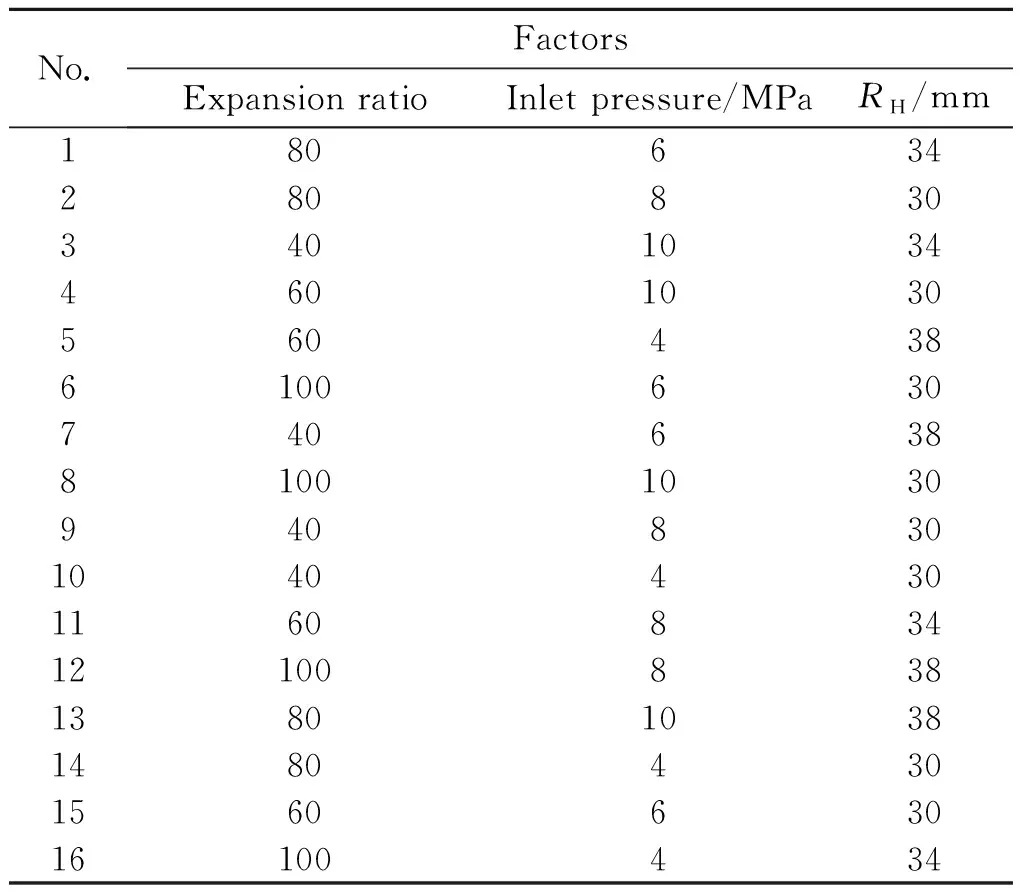
表2 混合型正交表Table 2 Mixed orthogonal table
2 结果与讨论
2.1 ATEDN典型工作模态分析
为了分析ATEDN在不同高度下的流场特征,此处以Case 5为例,将其典型工作模态下的流场和壁面压力分布进行对比,如图5所示。可以看到,在低空时(0~1.95 km),ATEDN尾流处于“开放”模式(图5(a)),高速燃气在塞锥末端发生流动分离形成剪切层。剪切层两侧分别为沿喷管外壁的超声速核心流和中心塞锥后方的亚声速回流区。由塞锥基底尖角处发出的入射激波撞击到喷管外壁面发生发射。从喷管外壁面压力分布曲线可以看到,喷管收敛段壁面压强有小幅下降,而进入喉部后则压强骤降,之后保持稳定。在喷管中后段,激波反射造成壁面压力的小幅度上升,随后逐渐降低至环境压力。将ATEDN的此工作模态称为开放-固壁反射模态(OW模态)。随着工作高度增加 (3.01~4.21 km,见图5(b)),喷管尾流虽然仍处于“开放”模式,但喷管内部超声速核心区面积增加,入射激波在喷管外壁面的反射点被推出喷管。此时激波发生自由边界反射,喷管外壁面压力在经过喉部之后保持恒定。将ATEDN的此工作模态称为开放-自由边界反射模态(OF模态)。当工作高度进一步增加(达5.57 km后,见图5(c)),ATEDN尾流“闭合”,使得塞锥基底处的小面积回流区无法受到外界环境压力变化影响,喷管壁面压力分布曲线与OF模态相同且不随工作高度的继续增加而改变。此处将ATEDN的这种闭合工作模态简称为C模态。
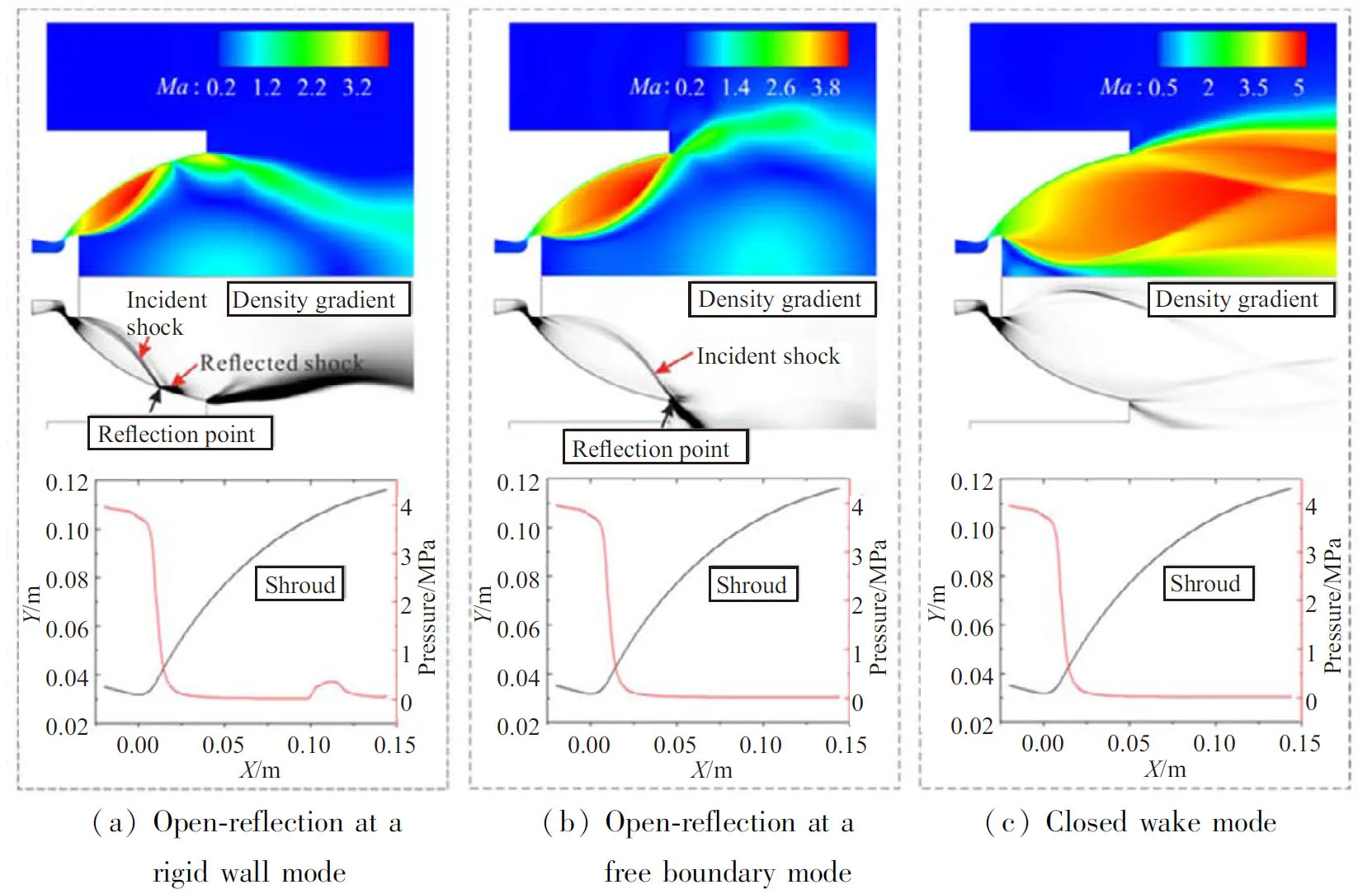
图5 Case 5在三种典型工作模态下的流场(上)及壁面压力(下)分布Fig.5 Flow fields (upper row) and pressure distributions(lower row) of Case 5 at three typical operating modes
对表2所示各组合方式下ATEDN的工作过程进行数值仿真,发现在0~31 km高度范围内,Case 5的三种典型工作模态并不总是出现在所有的喷管工作过程中。比如Case 2不存在OW模态,Case 3仅存在C模态,经过必要的算例补充后发现,Case 10和14存在非常短暂的OF模态,而Case 16的C模态发生在 7.2 km。将不同ATEDN所经历的典型工作模态及相对应的工作高度范围进行归纳,可将其工作过程分为以下三类:
(1)喷管全程处于闭合工作模态(Case 3、4、7、8、9、11、13);
(2)喷管先后经历OF和C模态(Case 2、12、15);
(3)喷管先后经历OW、OF和C三种工作模态(Case 1、5、6、10、14、16),归纳结果可见表3。
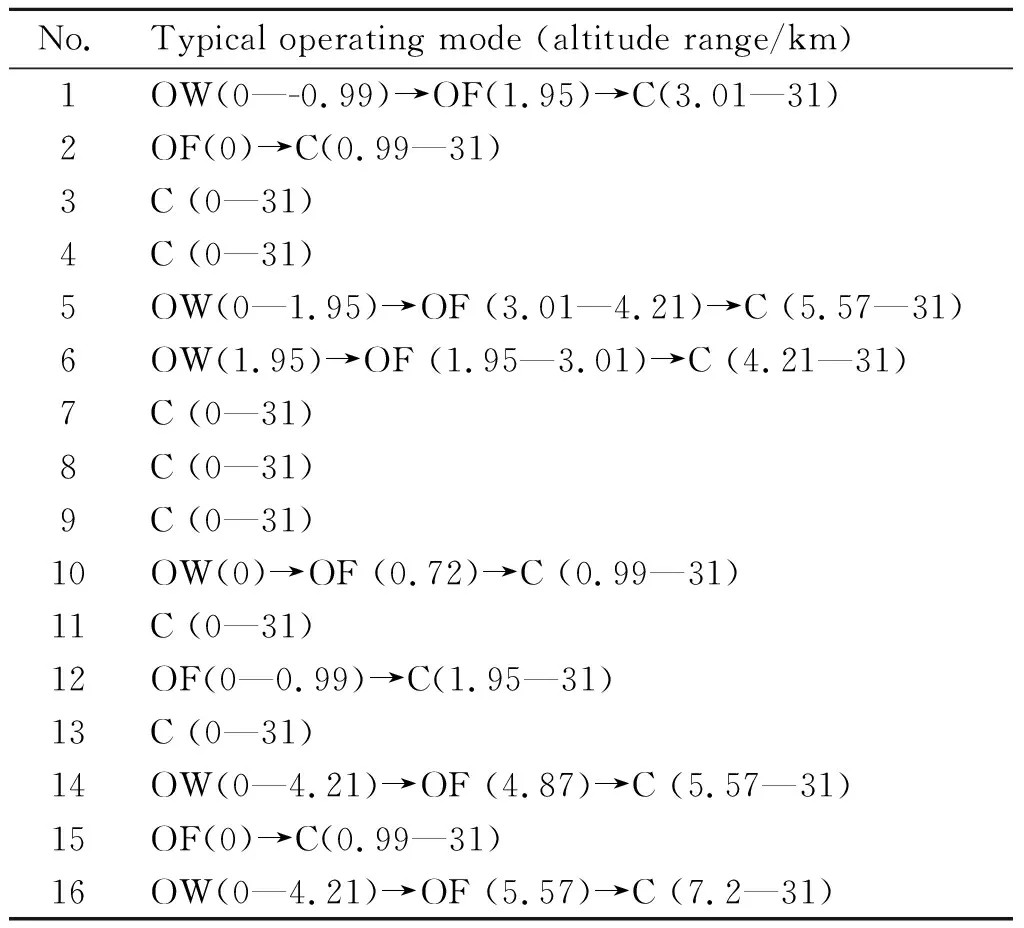
表3 ATEDN典型工作模态及对应的高度范围Table 3 Typical operating modes and corresponding altitude ranges of ATEDNs
选取Case 3对第一种工作过程(即全程C模态)的流场进行分析,图6为其在0、3.01、5.57 km高度工况下对应的马赫数分布图。可以看到,喷管尾流在海平面即处于“闭合”模态,这主要与喷管的入口压力和扩张比有关。通过多个喷管流场的对比结果可以看出,当扩张比和塞锥基底半径相同时,入口压力越大,喷管达到闭合模态所对应的工作高度越低;当入口压力和塞锥基底半径相同时,扩张比越小,喷管达到闭合模态时对应的工作高度越低。处于第一种工作过程的喷管或是入口压力足够大,或是扩张比足够小,使其在海平面即处于“闭合”工作模态。全程C模态使ATEDN失去了高度补偿能力,所以在喷管设计时应该尽量避免喷管在海平面即处于闭合模态的情况发生。
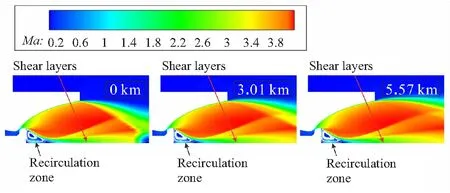
图6 Case 3在H取0、3.01、5.57 km的马赫数分布图Fig.6 Mach number distributions of Case 3 at H=0,3.01,5.57 km
图7为Case 2、12、15(均处于第二种工作过程,即由OF转变为C模态)在0、0.99、1.95 km工作高度的对应的马赫数分布云图。可以看出,在海平面工作条件下,激波反射点位于喷管外部,激波发生自由边界反射,工作高度增加后,喷管尾流处于“闭合”模式。
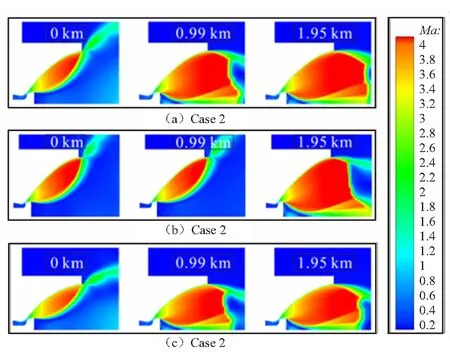
图7 Case 2、Case 12、Case 15(c)在H取0、0.99、1.95 km的马赫数分布图Fig.7 Mach number distributions of Case 2, Case 12 and Case 15 at H=0,0.99,1.95 km
绘制0~31 km高度范围内Case 2、Case 12和Case 15对应的喷管推力变化曲线,如图8所示。可以看出,随着工作高度的增加,Case 2、Case 12和Case 15对应的喷管推力逐渐增加。由式(7)可知,喷管推力由两部分组成,分别是燃气对喷管内表面的作用力Fin和外界大气对喷管外表面的作用力Fex。随着喷管工作高度的增加,喷管推力的Fin值变化很小,但是Fex的值却显著降低,此时喷管推力主要由喷管出口压差所产生,因此,其推力逐渐增加。
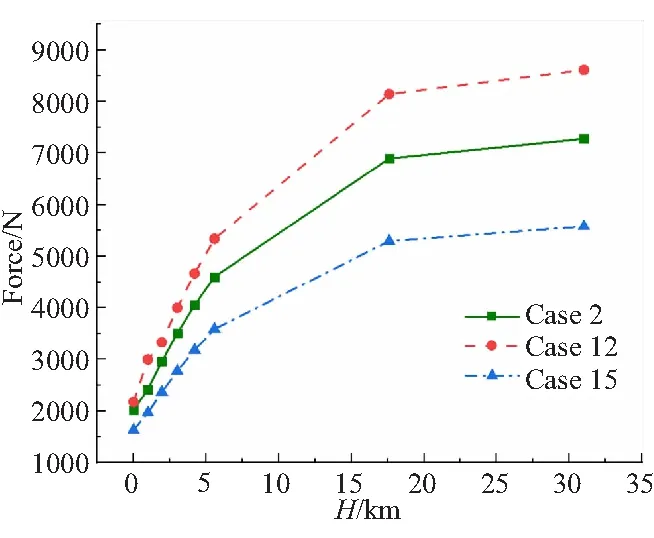
图8 第二种工作过程的推力随高度变化曲线Fig.8 Thrust histories with altitude variation of the second operating process
选取Case 5对第三种工作过程(即由OW转变为OF再转变为C模态)流场进行分析,图9为典型高度工况下其对应的马赫数分布图。可以看出,在0~ 1.95 km 处,喷管处于开放-固壁反射工作模态,入射激波在喷管壁面发生反射,当高度增加至3.01 km时,剪切层下移,喷管内高速核心区域增加,激波反射点移动至喷管出口外,剪切层上方的入射激波发生自由边界反射。当高度增加至5.57 km时剪切层与喷管轴线相交,塞锥下游的亚声速回流区不再与外界环境连通,喷管进入“闭合”工作模态。
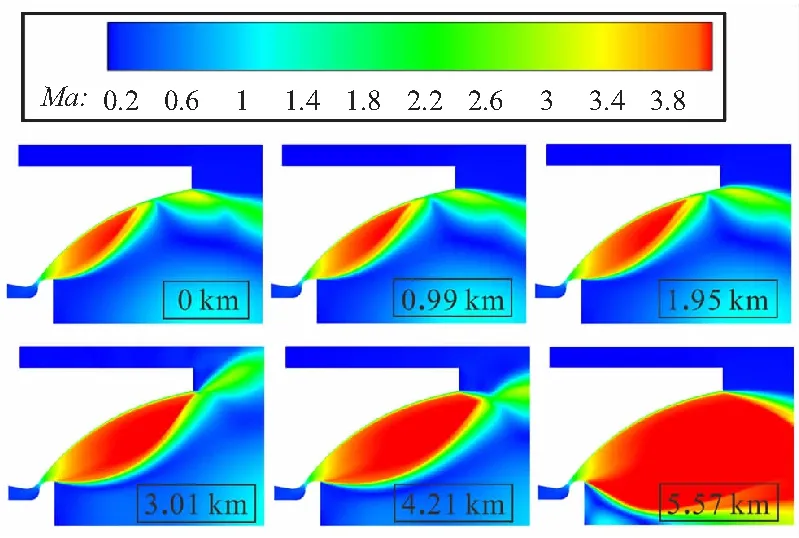
图9 Case 5在宽高度工况下的马赫数分布图Fig.9 Mach number distributions of Case 5 within wide height condition
图10为第三种工作过程的喷管推力随高度变化曲线。可以看到,Case 1、5、6对应的喷管推力先增加后减小后又增加;Case 16经历了2次推力增加和2次推力减小,Case 14经历了3次推力增加和2次推力减小。在该工作过程中,喷管推力变化情况较为复杂,由WANG等[15]的研究可知,这种推力的变化极大地受到喷管内激波位置和激波强度的影响。
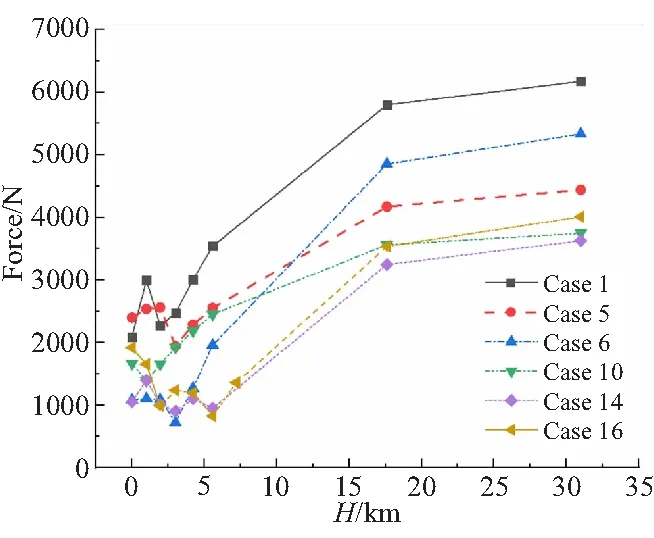
图10 第三种工作过程的推力随高度变化曲线Fig.10 Thrust histories with altitude variation of the third operating process
在由开放-固壁反射到开放-自由边界反射的模态转换过程中,喷管均出现推力骤减现象,这一现象可利用壁面压强变化进行解释。以Case 5为例,其喷管所对应的Fin和Fex随工作高度变化曲线如图11所示。
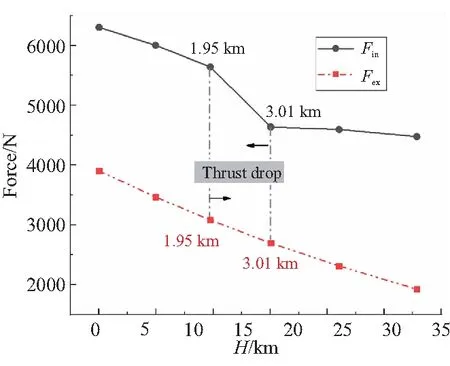
图11 Case 5的Fin和Fex随高度变化曲线Fig.11 Fin and Fex histories with altitude variation of Case 5
由图11可见,随着工作高度增加,Fin和Fex均逐渐减小。由于在模态转换过程中(1.95~3.01 km),ATEDN喷管内部的高速核心流区域扩大,激波反射点被逐渐推出喷管,喷管扩张段壁面的局部高压区消失,使得Fin骤减,且其减小值要显著大于Fex的减小值。因此,在该模态转换过程中,喷管的总推力出现短暂的骤减现象。
2.2 正交法分析影响因素
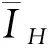
(8)
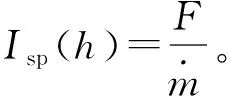
表4为正交模拟计算结果。正交设计法所采集的数据常用极差分析法进行处理。极差表示某一因素在所有水平条件下性能参数最大值与最小值之间的差值,此处的极差大小反映各因素对喷管性能影响的主次关系。极差的计算公式为
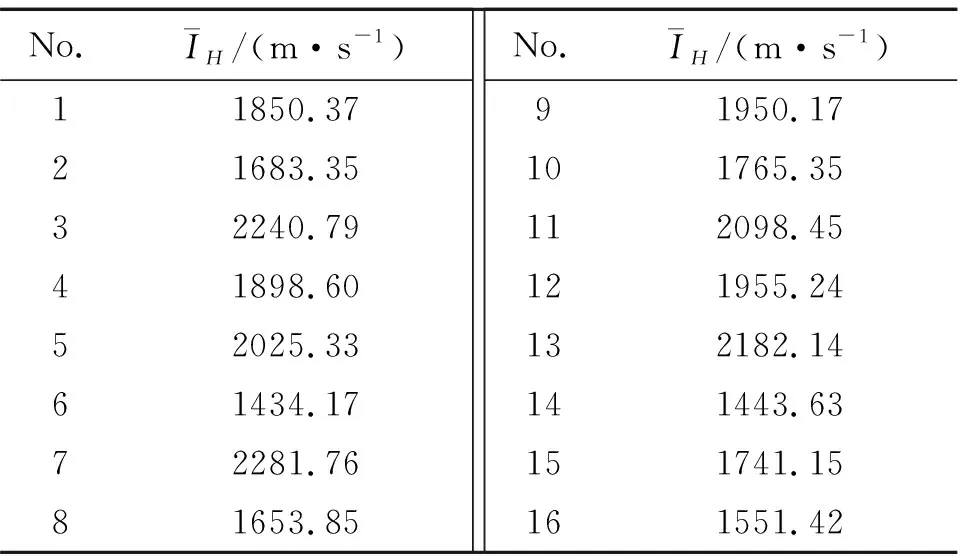
表4 正交模拟结果Table 4 Orthogonal simulation results
(9)
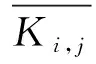
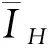
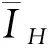

图12 三个因素不同水平时高度积分平均比冲变化曲线Fig.12 Altitude-integral average specific impulse of the three factors at different levels
3 结论
本文对环喉式膨胀偏流喷管的流动过程进行了数值仿真计算,采用正交法和极差分析法研究了扩张比、入口压力和塞锥基底半径对喷管性能的影响及其重要程度,得出如下结论:
(1)ATEDN在不同高度工况工作时,存在开放-固壁反射(OW模态)、开放-自由边界反射(OF模态)和闭合(C模态)三种典型工作模态。研究发现,喷管在0~31 km高度范围内存在三类不同的工作过程:喷管全程处于C模态;喷管先后经历OF和C模态;喷管先后经历OW、OF和C三种工作模态。
(2)ATEDN的不同工作过程表现出不同的推力变化特性。对于第二种工作过程,ATEDN推力逐渐增加;对于第三种工作过程,喷管推力变化情况较为复杂,且在由OW模态到OF模态的转换过程中,喷管推力出现骤减。
