爆震波逆向传播抑制特性数值仿真

2023-07-08张彦军严凯威王晓东王卫星

航空发动机 2023年2期

张彦军，严凯威，王晓东，王卫星

（1.中国航发沈阳发动机研究所，沈阳 10015；2.南京航空航天大学能源与动力学院，南京 210016）

0 引言

与传统布雷顿循环方式相比，基于爆震燃烧构建的热力学循环效率理论上可提高近50%，其具有低耗油率、自增压和能量释放率高的优点。因此，基于爆震燃烧模式的推进系统具有较大的潜在优势[1-2]。目前采用爆震燃烧方式的发动机有脉冲爆震发动机、旋转爆震发动机和斜爆震发动机[3]。

19 世纪60 年代，Abel[4]和Berthelot 等[5]对爆震波传播速度进行了系统研究；1900年左右，Chapman[6]和Jouguet[7]提出了C-J 理论，可精确预测爆震波前后的物理参数。在理论研究基础上，近年来爆震发动机在工程应用上取得了长足进展。Schauer[8]开展了以脉冲爆震发动机为动力的飞行试验；刘世杰等[9]模拟自由射流对旋转爆震冲压发动机整机进行试车，实现了稳定传播的旋转爆震波并初步测得其频率；张子健等[10]开展了斜爆震流场数值仿真研究，实现了超声速气流中斜爆震波的起爆和驻定燃烧。

冲压爆震发动机主燃烧室工作时压力脉动十分剧烈，其与进气道之间缺乏机械隔离部件，爆震波产生的非定常压力脉动前传，会使进气道发生流场振荡，严重时可能影响进气道流场，进而干扰到发动机正常工作[11]。Fotia 等[12]对一种冲压脉冲爆震发动机燃烧室中爆震波对进气的影响进行了研究；莫建伟等[13]建立了旋转爆震发动机周期性反压简化模型，发现在周期性反压作用下进气道性能与稳态情况下基本一致；张鑫[14]对冲压旋转爆震发动机隔离段进行了研究，表明改变隔离段构型可有效抑制斜激波前传，对流场稳定带来不利影响。常见的消波手段多种多样，如壁面孔洞[15]、节流板[16]和扩容室[17]等。

从对国内外研究现状分析可知，目前对于爆震燃烧在试验与仿真方法、流动机理方面已经有了较为深入的研究，爆震发动机设计也取得了长足发展，已经开始工程研制。而对爆震冲压发动机扩张段内强压力扰动主导的复杂非定常流动及抑制技术研究相对较少。本文在爆震工作条件下开展基于刚性障碍物的扰动传播抑制技术研究。

1 物理模型与计算方法

本文研究对象为爆震冲压发动机扩张段，借鉴直连试验的思路，设计一拉瓦尔喷管将气流加速至超声速近似模拟进气道喉道下游流场，同时对进气道扩张段进行简化将其设计为环形的等直涵道即进气涵道，带刚性障碍物进气涵道物理模型如图1所示。图中H为障碍物高度，D为障碍物间距，α为障碍物顶角角度，h为进气涵道出口高度。进气涵道扩张段面积扩张比为2.0，当量扩张角为1.14°。本文着重开展强扰动逆向传播抑制技术，在保留涵道出口高频强扰动主要特征的前提下，开展2 维轴对称非定常计算，以便开展获得关键流动特性与设计参数。进气涵道左侧为进口，给定压力进口边界条件；右侧为出口，给定压力出口边界条件；上下均设置为壁面。采用结构化网格划分，壁面底层网格尺寸为0.01 mm，沿流向最大网格尺度为1 mm，总网格量约为19万。

图1 带刚性障碍物进气涵道物理模型

来流条件见表1。

表1 来流条件

在爆震发动机正常工作时，下游燃烧室会产生高频爆震波，产生周期性的强压力扰动，该强压力扰动以运动激波的形式向上游传播。本文采用文献[18]中给出的正弦脉动压力公式描述出口压力边界条件

式中：p*为涵道进口来流总压；p*为来流总压；A为压力振幅；B为形状因子，改变形状因子B可以改变高压区域在整个周期时间的比例；C为恢复区压力。

通过改变A、B和C的值，能够获得不同压力振型的爆震波。本文所研究的出口高频脉动压力随时间变化曲线如图2 所示。压力脉动频率为2000 Hz，峰值压力为1.4p*，恢复区压力为0.76p*，时均压力均为0.79p*。

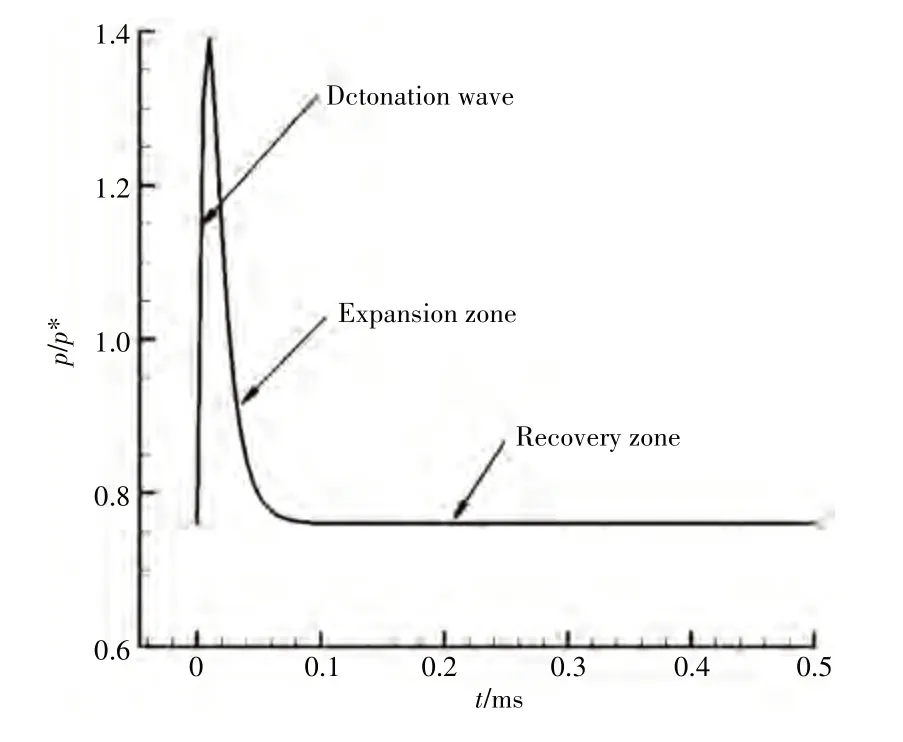
图2 高频脉动压力随时间变化

本文采用定常/非定常计算方法开展研究工作，求解全粘性Navier-Stokes方程，选择近似牛顿迭代双时间步（dual-time-step）开展非定常计算。选用隐式格式的时间推进以加速计算收敛和保持计算稳定，空间离散采用2 阶迎风格式，无粘通量分裂格式采用AUSM 格式，黏性通量采用2 阶中心差分格式离散。湍流模型取用k-ω- sst 2方程模型，sst模型适合用于含有逆压力梯度的流动，计算精度高，应用范围广。气体选取理想气体，考虑比热随温度的变化，其中粘性系数采用Sutherland公式求解

比热比采用5次多项式拟合

式中：μ为黏性系数；μ0为标准大气压下0 ℃条件下的黏性系数；T为气体温度；T0=273.15 K；K为常数；与气体性质有关；Cp为比热比。

本文主要研究旋转爆震发动机燃烧室进气涵道流动特性，涉及到运动激波前传、运动激波/边界层干扰、运动激波衰减等诸多复杂流动现象，对非定常数值计算方法的精度要求较高，需要对数值计算方法进行校验。

采用Bruce等[19]的试验结果验证扰动传播计算方法的准确性。Bruce 试验中来流马赫数为1.4，壁面滞止压力为0.14 MPa，试验模型出口处放置一椭圆形凸轮，凸轮旋转使出口处产生变化接近正弦脉动的压力。此脉动压力振幅约为时均压力的4%，频率为43 Hz。1 个周期内监测点压力脉动曲线与结尾激波位置的动态变化曲线对比如图3 所示。从图中可见，数值计算结果与Bruce 试验结果吻合。因此本文所采用的非定常数值仿真方法能够较为精确地模拟运动激波主导的复杂流动，适用于本文研究内容。

图3 1个周期内监测点压力脉动曲线与结尾激波位置的动态变化曲线对比

采用Izumi等[20]开展的运动激波聚焦反射试验对本文采用的计算方法校核，其中激波运动马赫数为1.5。运动激波聚焦反射过程中不同时刻的流场结构如图4 所示。其中上半图为试验纹影图谱，下半图为数值仿真结果，时间t采用z1/2D/a进行了无量纲化处理，符号为t͂。从图中可见，所采用的非定常计算方法能够较准确模拟出运动激波传播过程中复杂的流场结构变化。

图4 运动激波聚焦反射过程中不同时刻的流场结构

由上述2 个典型非定常算例校核结果可知，本文所采用的非定常计算方法满足本课题的研究需求。

本文所研究的流动涉及运动激波传播、运动激波激波/边界层干扰等复杂流动现象，而网格尺度与数量对复杂流场分辨率有很大影响，需要开展网格无关性分析。本文共对比分析了3 套不同空间分辨率的网格，底层网格尺寸分别取0.005、0.010 和0.030 mm，2 维轴对称网格总量分别为13 万、18 万和23 万，分别命名为coarse mesh、fine mesh 和refine mesh。采用上述3 套网格计算得到的同一时刻进气涵道中心线和下壁面沿程压力分布曲线如图5 所示，同一位置进气涵道局部马赫数等值如图6 所示。从图中可见，3 套网格计算得到的压力沿程分布规律一致。与粗糙网格和稠密网格相比，中等密度网格计算得到的中心线压力峰值相对误差分别为1.21%、0.21%，下壁面压力峰值相对误差分别为2.57%、0.44%；不同网格计算得到的流场结构基本相同。为保证计算精度同时兼顾计算工作量，本文选取fine mesh 开展数值仿真研究，其底层网格尺寸为0.01 mm。

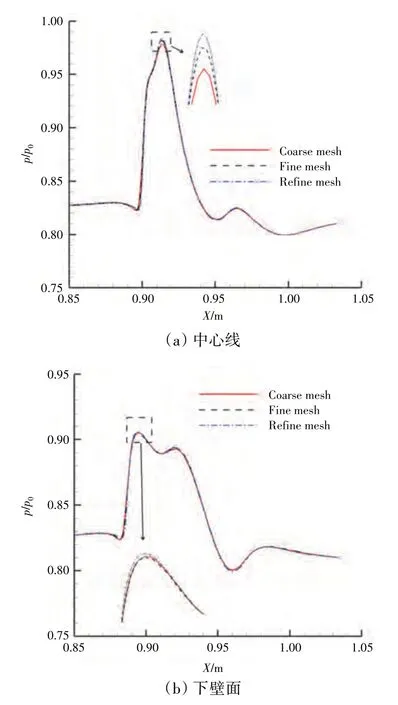
图5 同一时刻进气涵道中心线和下壁面沿程压力分布曲线

图6 同一位置进气涵道局部马赫数等值

2 强压力扰动下进气涵道流动特性分析

爆震工作条件下，进气涵道内出现逆向传播的运动激波。1 个周期时间内进气涵道流场演化过程如图7 所示。从图中可见，受出口强压力脉动影响，涵道内存在逆向传播的运动激波。图中黑色虚线代表同一道运动激波在不同时刻所处位置，虚线斜率即表征激波运动速度，随着时间推移，运动激波逐渐向上游运动，虚线斜率增大，运动激波间距缩小，这表明运动激波传播速度逐渐降低，并最终在结尾激波下游滞止演化为驻激波，进而屏蔽下游扰动对上游流场的影响。气流经过运动激波压缩后马赫数迅速降低，随后受波后膨胀影响，马赫数逐渐增大；而后流经下一道运动激波，重复这一过程，流场存在周期性变化。由图还可看出，与定常反压状态相似，涵道内流场结构非对称，内壁面附近气流马赫数明显低于外壁面附近气流，运动激波靠近壁面一侧。分析认为内壁附近边界层较厚，运动激波与当地边界层干扰，进一步增大了边界层厚度。同时还注意到出口强压力扰动诱发结尾激波位置出现明显振荡。

图7 1个周期时间内进气涵道流场演化过程

受边界层与运动激波/边界层干扰影响，运动激波形态整体上呈现“λ”波特征，近壁面为斜激波，中部接近正激波。同时运动激波逆向传播过程中，中部接近正激波部分逐渐减小。

1 个周期内进气涵道内流场压力等值如图8 所示。从图中可见，来流经过运动激波压缩后压力迅速升高，随后受波后膨胀影响，压力缓慢下降。与马赫数图对应，流场也呈现非对称状态，由于内外壁面边界层厚度差异较大，明显看出运动激波压力峰值位置更靠近外壁面。

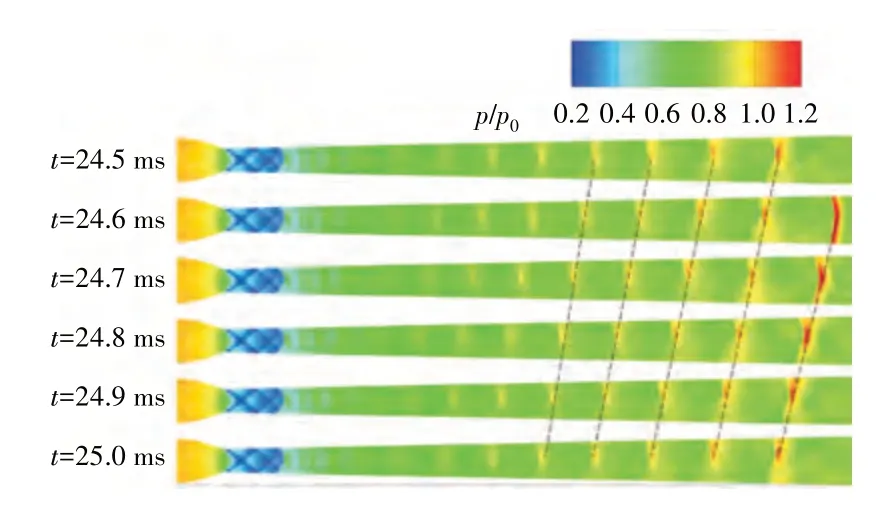
图8 1个周期内进气涵道内流场压力等值

1 个周期内进气涵道内中心线沿程压力分布曲线如图9 所示。从图中可见，随着进气涵道内受出口脉动压力影响产生的运动激波连续向上游传播，压力峰值与谷值逐渐下降，且运动激波间距减小，进一步表明运动激波传播速度逐渐降低。结尾激波位置随时间基本不发生变化。

图9 1个周期内进气涵道内中心线沿程压力分布曲线

进气涵道运动激波强度与传播速度沿程分布曲线如图10 所示，其中p2为运动激波波后压力，p1为运动激波波前压力，速度为绝对坐标系下运动激波逆向速度。从图中可见，运动激波逆向传播过程中强度先迅速衰减，前传约0.12 m 后强度衰减速率减小，至X=0.3 m 附近，激波强度达到最小值，随后缓慢升高，详细分析将在下文给出。从图中还可见，运动激波逆向传播过程中，传播速度一直下降直至为0，此时运动激波演化为驻激波。

图10 进气涵道运动激波强度与传播速度沿程分布曲线

涵道内存在逆向传播的运动激波，必然诱发压力脉动，为反映该压力脉动的强度，引入压力无量纲标准差进行评价

式中：ε为涵道内某监测位置处无量纲标准差；pi为采样瞬时压力为监测位置处时均压力；n为采集数据量。

本文取2 个完整周期数据量。ε值越大，表征压力脉动强度越大。

基于质量流量平均进气涵道沿程压力脉动强度分布曲线如图11 所示。从图中可见，随着运动激波在涵道内逆向传播，压力脉动强度先减小，至C 点到达谷值，后增大在B 点处出现极大值，随后迅速减小至0。依据压力脉动强度分布，进一步可将整个进气涵道可分为2 段，OA 段为未受运动激波干扰区，AD段为运动激波干扰区；其中AD 段可继续细分：AC 段为当地速度主导区域，CD 段为运动激波主导区，各区详细解释将在下文分析。

图11 基于质量流量平均进气涵道沿程压力脉动强度分布曲线

1 个周期内流场演化过程如图12 所示。爆震工作条件下存在明显的运动激波逆向传播。图12（a）刻画了截面D→C流场演化过程，从图中可见，运动激波由出口向上游传播，传播过程中运动激波空间上逐渐向外壁面靠近并且变小，分析运动激波轨迹可知其传播速度下降。图12（c）详细描绘了运动激波传播速度逐渐下降直至为零，运动激波演化为驻激波的过程。

图12 1个周期内流场结构演化过程

由上述分析可知，爆震工作条件下涵道内存在逆向传播的运动激波，气流经过运动激波后马赫数降低，压力升高；随后气流膨胀，压力降低。运动激波在逆向传播过程中强度先迅速衰减，后增大，而传播速度逐渐下降直至为零。

3 刚性障碍物对运动激波传播特性影响

3.1 刚性障碍物对涵道流动特性影响

本节开展刚性障碍物对涵道流动特性影响研究，在物理模型（图1）中，障碍物高度H=0.05h，障碍物间距D=3H，顶角α=45°。

带刚性障碍物进气涵道1 个周期内流场演化过程如图13 所示。从图中可见，整体上与无刚性障碍物涵道流场结构相似，受出口强压力脉动影响，涵道内存在逆向传播的运动激波，运动激波传播速度逐渐降低。运动激波形态整体上呈现“λ”波特征，运动激波逆向传播过程中，中部接近正激波部分逐渐减小。

图13 带刚性障碍物进气涵道1个周期内流场演化过程

运动激波流经刚性障碍物演化过程如图14 所示。从图中可见，受刚性障碍物影响，运动激波进入进气涵道后波根处气流被障碍物阻挡，速度降低。中间正激波部分基本不受干扰，整体上运动激波形态由弯曲向平直演化，如III、IV图所示。

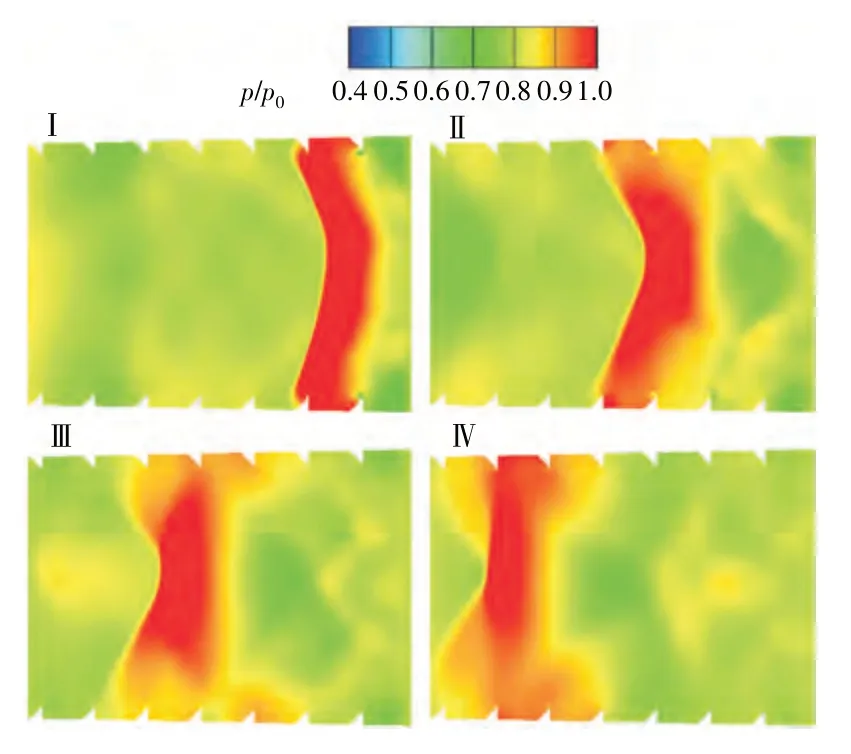
图14 运动激波流经刚性障碍物演化过程

带刚性障碍物进气涵道压力脉动强度沿程分布如图15 所示。从图中可见，带刚性障碍物进气涵道压力脉动强度分布与基准涵道规律一致，随着运动激波逆向传播压力脉动强度先减小后增大，至结尾激波下游达到极大值，后快速衰减直至为零。刚性障碍物影响压力脉动强度，与基准涵道相比，在刚性障碍物位置处，进气涵道压力脉动强度衰减速率加快；谷值降幅较小，所在位置后移；极大值略有上升，所在位置前移。

图15 带刚性障碍物进气涵道压力脉动强度沿程分布

带刚性障碍物进气涵道运动激波逆向传播马赫数、波前当地马赫数与相对马赫数沿程分布如图16所示。从图中可见，带刚性障碍物进气涵道沿程马赫数分布与基准涵道相一致，运动激波逆向传播马赫数沿逆向逐渐减小，绝对坐标系下波前来流马赫数沿逆向逐渐增大，波面坐标系下相对马赫数沿逆向先减小后增大。在刚性障碍物位置处，与基准涵道相比，运动激波逆向传播马赫数下降。绝对坐标系下波前来流马赫数上升，这是由于气流进入刚性障碍物区域后，流管收缩，气流加速，马赫数增加。在二者共同作用下，波面坐标系下相对马赫数下降速率更快，更快达到谷值。

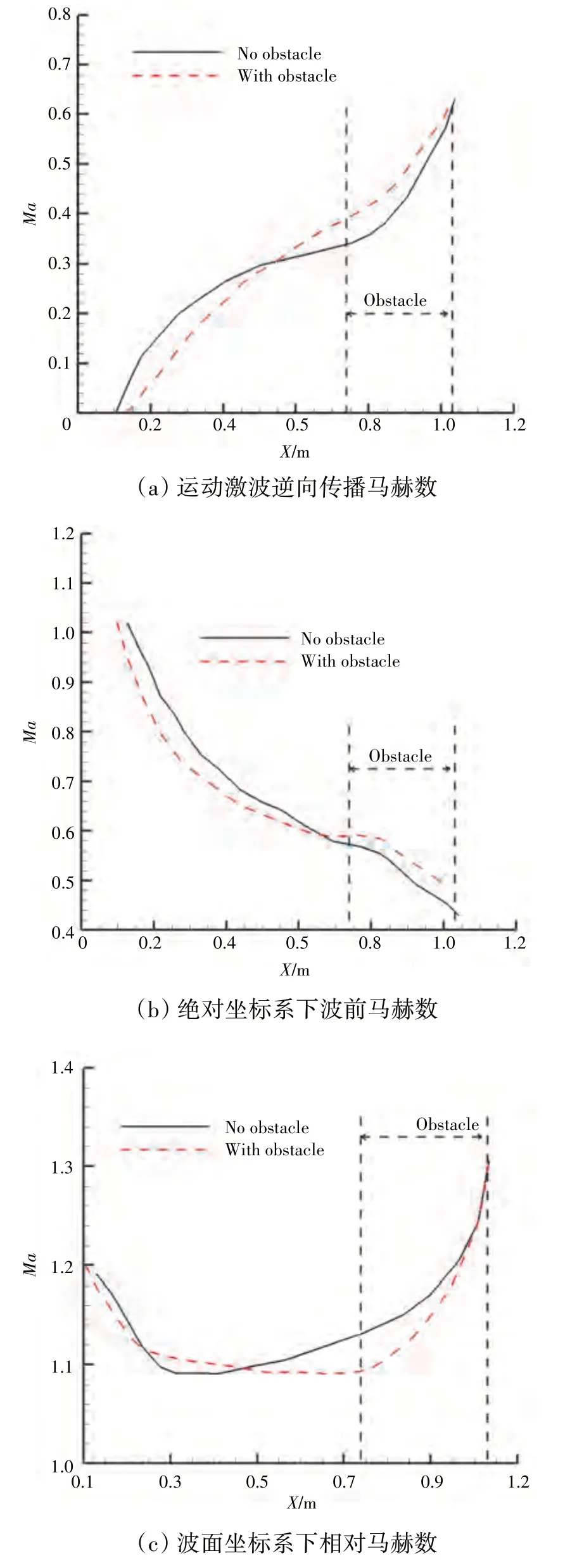
图16 带刚性障碍物进气涵道运动激波逆向传播马赫数、波前当地马赫数与相对马赫数沿程分布

由以上分析可知，刚性障碍物可有效加快运动激波衰减速率。添加刚性障碍物对压力脉动强度谷值影响较小，可以缩短到达谷值所需距离。

3.2 刚性障碍物高度对涵道流动特性影响

本节研究刚性障碍物高度对涵道流动特性的影响，在物理模型（图1）中，在保证刚性障碍物安装位置、形状以及间距不变的前提下，改变障碍物高度H。

在爆震工作条件下，不同刚性障碍物高度进气涵道流场结构如图17 所示。从图中可见，添加刚性障碍物后，结尾激波前移，流场不对称性降低。随着障碍物高度增大，结尾激波逐渐向上游移动，如图中黑色实线所示。结尾激波位置决定波前马赫数，影响结尾激波强度，进而影响激出口总压恢复。对于本文研究的超声速扩张涵道，结尾激波越靠近喉道，波前马赫数越小，激波强度越弱，总压损失越小，涵道出口总压恢复越高。在障碍物位置处，核心流经过运动激波所形成的低速区逐渐减少，运动激波强度逐渐减弱。由局部放大图可知，不同障碍物高度下，障碍物之间均被一个涡旋完全占据，障碍物高度范围内几乎全为低速区；障碍物高度越高，该低速区越大。

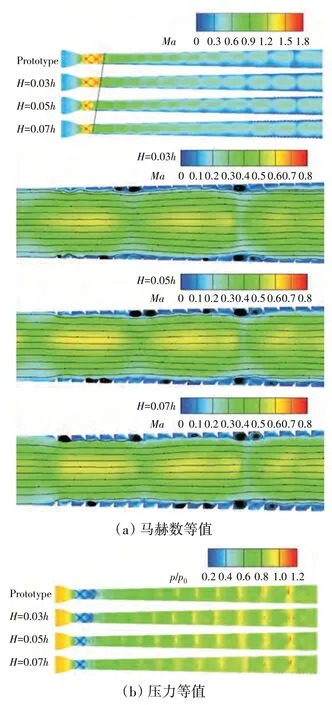
图17 在爆震工作条件下，不同刚性障碍物高度进气涵道流场结构

在爆震工作条件下，不同刚性障碍物高度进气涵道中心线参数沿程分布如图18 所示。从图中可见，与基准涵道相比，结尾激波下游运动激波压力峰值和谷值升高，马赫数峰值和谷值降低。随着障碍物高度增加，结尾激波向上游移动。

图18 在爆震工作条件下，带刚性障碍物进气涵道中心线参数沿程分布

不同刚性障碍物高度进气涵道运动激波强度和逆向传播速度沿程分布曲线如图19 所示。从图中可见，添加障碍物后，在障碍物位置，激波强度衰减速率加快；激波前传速度下降。随着障碍物高度增加，激波强度下降，激波前传速度先减小后增大。

图19 带刚性障碍物进气涵道运动激波强度和逆向传播速度沿程分布

不同刚性障碍物高度进气涵道压力脉动强度沿程分布如图20所示。从图中可见，添加障碍物后，H=0.03h构型与基准构型压力脉动强度分布基本一致。随着障碍物高度增加，压力脉动强度谷值先略微增大，后减小，谷值位置后移。

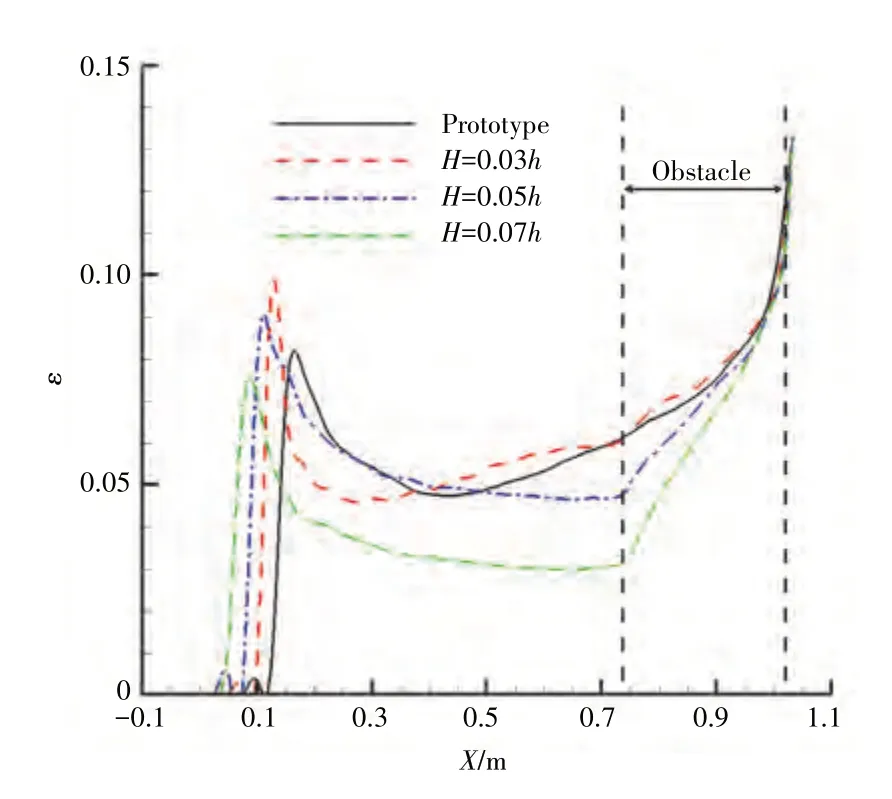
图20 不同刚性障碍物高度进气涵道压力脉动强度沿程分布

在爆震工作条件下，不同障碍物高度进气涵道性能参数见表2。从表中可见，添加刚性障碍物后，涵道出口马赫数和总压恢复系数增大。随着障碍物高度增加，涵道出口马赫数和总压恢复系数增大。分析认为这主要是由于结尾激波前移，波前马赫数降低，结尾激波强度减弱，总压损失减小。与基准构型相比，不同障碍物高度下进气涵道压力脉动强度谷值均降低，最大降幅为36.6%。