脉冲爆震涡轮发动机转子系统优化设计

2023-07-08王福斌郑龙席郑召利

航空发动机 2023年2期

傅超，王福斌，郑龙席，路宽，郑召利

（西北工业大学智能飞行器结构强度与设计研究所1，动力与能源学院2：西安 710072；3.武汉第二船舶设计研究所热能动力技术重点实验室，武汉 430205）

0 引言

近年来，脉冲爆震燃烧设计的涡轮发动机（Pulse Detonation Turbine Engine，PDTE）因其循环热效率高、具有自增压的特点而受到了国内外航空工业相关研究人员的广泛关注[1-2]。相比早期的脉冲爆震发动机（Pulse Detonation Engine，PDE）将高温高压燃气直接排向大气[3]，PDTE 则可通过涡轮传输部分能量，提高能量利用率的同时实现了发动机的静止起动。因此，PDTE 在民用、军用飞行器及超声速导弹上均有广阔的应用前景，对现代化经济和国防建设具有重要意义[4-5]。

从国内外研究现状来看，目前PDTE 的研究主要集中在点火和起爆方法[6-7]、燃烧室设计与传热分析[8-9]以及总体性能[10-11]方面。Hutchins 等[12]针对脉冲爆震发动机工作时的燃烧规律和能量传播特性进行了研究，讨论了不同压力下发动机工作的效率；Reddy[13]提出了一种新的燃气涡轮发动机中波转子和爆震发动机的集成方法，通过比较工作和热效率发现此方法有利于提高发动机的整体性能；Alsi 等[14]提出了用于脉冲爆震燃烧非定常激励的1 维欧拉气体动力学分析方法，并基于3 维有限元分析结果对比验证了所提方法的正确性。PDTE总体设计包括根据循环参数进行压气机、涡轮及燃烧室等设计，然后基于压气机和涡轮的尺寸和级数进行转子系统设计。转子系统的设计又包含支承方案设计、支点布局及系统各部位的几何参数确定，即转子系统必须满足总体设计在结构布局和尺寸上的要求，还要支撑发动机总体性能的实现。因此，除了在基本的结构尺寸方面必须服从总体设计以外，对转子系统在脉冲爆震气动载荷和不平衡量作用下的动力学特性也必须进行研究。张越等[15]还分析了机动飞行下转子系统的振动特性。与传统航空发动机不同，在PDTE 工作时作用在转子系统上的气动载荷具有显著的非定常性和周期性。在对PDTE 转子系统建模分析的过程中，必须考虑弯曲、扭转和轴向3 方面的振动，增加了转子动力学特性的分析难度；李胜远等[16]阐述了基于有限元法分析转子3 个方向振动的步骤并针对某模型转子进行了数值计算。在设计转子时，一般希望在包含工作转速在内的转速范围内，转子的振动幅值不超过某一限定值或使其最小化；傅超等[17]从转子系统加速启动振动响应中识别不平衡量大小，以便进行平衡而降低振幅。同时，为避免共振，要求临界转速距离工作转速存在20%以上的安全裕度。这些要求给转子系统的设计提出了很大的挑战，而优化算法在解决此类问题时具有较高的可行性。

本文根据总体设计要求构建了转子系统的初步结构，建立了其弯曲、扭转和轴向耦合有限元分析模型，考虑脉冲爆震气动载荷开展了动力学特性分析，并采用多目标优化算法基于临界转速裕度和振幅对转子系统进行了设计优化。

1 转子系统设计及动力学特性分析

1.1 转子系统初步设计

根据某PDTE 总体设计方案，转子系统设计为单转子构型，包含2 级风扇、4 级压气机和3 级涡轮，如图1 所示。发动机的设计转速为30360 r/min，慢车转速为7107 r/min。风扇、压气机及涡轮的进、出口总参数（温度、压力）、各级叶盘的质量和几何尺寸均由总体设计给出。该转子为细长结构，根据国内外先进航空发动机转子系统支承方案设计经验及基于本文转子模型的前期仿真研究，为避免过大支反力及便于调节临界转速与工作转速之间的裕度考虑，采用1-1-1支承方案。在转子两端采用棍棒轴承支承，仅承受径向载荷；中间采用止推轴承支承，既承受径向载荷又承受轴向载荷。该转子系统整体上属于薄壁盘鼓-轴承空心结构形式，以减轻整机质量。

图1 转子系统结构

上述转子-轴承系统可通过有限单元法进行离散和建模，然后基于数值方法进行求解其模态和动力学响应特性，以便后续调整和优化。

1.2 转子动力学特性有限元分析

基于有限元法将转子系统离散为Timoshenko 梁单元、刚性盘单元及轴承单元，其中梁单元包含了剪切效应。与转子系统常规有限元分析不同的是，为了考虑非定常、周期性气动载荷的影响，本文中每个节点包含了6个自由度，即节点的完全自由度向量Ue为

式中：x、y、z为节点在3 个坐标轴方向上的平动位移；θxθy,θz为节点在各平面内的转动位移。

每个单元包含2个节点，共12个自由度。单元内任意位置的位移可通过连续轴段的形函数插值求得。对于各种类型的单元，其运动方程和单元矩阵的推导过程见文献[18]。气动载荷对单元矩阵有一定影响，不能忽略。例如在发动机工作时产生的扭矩和轴向力会给梁单元施加附加刚度项ka和km[16]

式中：fa和fm为作用在单元上的轴向力和轴向扭矩；L为轴单元长度；Ny和Nz为形函数。

完成每个单元的建模后，基于Lagrange 方程推导出转子系统的运动微分方程

式中：M、C、K和G分别为转子系统的质量矩阵、阻尼矩阵、刚度矩阵及陀螺矩阵；Ω为系统的转速；Fg为重力；Fu和Fp分别为不平衡激励和气动载荷激励；φ为不平衡激励力加在对应的节点上，其大小为

式中：m为质量不平衡量；e为偏心距；φ为不平衡激励的初始相位。

在不考虑压力反传的条件下，压气机受到的轴向力近似为常数，方向向前。涡轮转子在脉冲爆震燃烧室（pulse detonation combustion，PDC）不燃烧时，同样受到固定幅值的轴向力作用，方向向后。当PDC发生燃烧反应而产生脉冲冲击时，给涡轮转子1 个向后的高幅值轴向力冲击。因此，在连续的工作循环下，涡轮转子受到周期性的脉冲冲击轴向力作用。压气机转子和涡轮转子所受的扭矩具有幅值相等而方向相反的特点，因而无论PDC 是否产生脉冲冲击，二者所受的扭矩均为时变周期性的。设PDC 工作频率为fpdc，当PDC 不燃烧时，压气机转子上所受向后的轴向力为A1，轴向转矩大小为M1，涡轮上所受向前的轴向力为A2，轴向转矩大小为M1；当PDC 发生燃烧时，压气机转子上的轴向力不变，涡轮转子上所受轴向力变为A3，压气机转子和涡轮转子上所受转矩大小为M2。根据以上分析，PDTE 转子上所受到的冲击力载荷在时域描述为

式中：t为时间；Hpdc= 1/fpdc，为PDC 的燃烧工作周期；Fcomp为压气机转子所受轴向力；Mcomp为压气机所受轴向扭矩；Fturb为涡轮转子所受轴向力；Mturb为涡轮转子所受轴向扭矩。

其中力矩的正负可通过规定的正方向和右手定则确定。建立了非定常周期性气动载荷的力学模型后，转子系统的运动微分方程可采用数值积分法求解[19]，如Newmark-β法和Runge-Kutta法。

2 基于NSGA-II的转子优化设计

航空发动机转子系统工作环境恶劣、分支结构众多，特别是PDTE 中存在的脉动式气动载荷给转子的设计带来了新的挑战。对于满足总体设计基本要求后的转子结构，还应根据临界转速裕度要求对支承位置、支承刚度及几何参数等进行优化，使得转子在目标范围内临界转速处的振幅最小化，达到控制振动的目的[20]。这一优化过程涉及优化目标设置、优化变量选取及约束条件构建等。本文转子的多目标优化设计问题可表述为

式中：di（g，h）为临界转速处的振幅；aj≤gj≤bj为不等式约束条件≤hk≤为各设计参数，上划线和下划线分别表示其上下限；Ωj为发动机怠速和工作转速；ωi为与Ωj相近的临界转速，二者的差异作为临界转速裕度约束。

第2 代非支配遗传算法（Non-dominated Sorting Genetic Algorithm II，NSGA-II）的基本思路是通过对种群中的个体进行非支配排序并分级，测算各个体的拥挤距离，最终获得满足终止条件的近似解。在本文的优化计算中，以两端轴承的支承刚度、止推轴承的支点位置及转子壁厚作为设计变量，根据抗拉和抗扭强度校核壁厚不应低于6 mm，以参数取值范围和临界转速裕度为约束条件，以共振幅值最小化作为优化目标。

3 结果与讨论

在仿真计算中，图1 中转子的轴段长度L1～L10分别为0.02、0.02、0.08、0.045、0.065、0.04、0.20、0.72、0.04、0.08、0.030、0.03 m。转子材料的弹性模量E=2.1×1011N/m2，密度ρ=7850 kg/m3，泊松比σ=0.3。在优化前后，转子上的激振力均由相同大小的不平衡量产生，其值为1×10-5kg/m。止推轴承位于距离转子左端0.38 m 处。轴承1、3 的径向刚度、轴承3 的径向和轴向刚度以及转子壁厚b等优化设计参数的初始值见表1。

表1 转子物理参数

在脉冲爆震燃烧过程中产生的轴向力会引起转轴内部拉伸正应力，轴向扭矩产生切应力，气动扭矩附加的切应力效应远比气动轴向力产生的正应力效应大。根据总体设计中压气机和涡轮的几何尺寸和进、出口压力可估计作用的轴向力和扭矩大小。忽略发动机工作时短暂的填充和排气过程，设燃烧室燃烧频率为20 Hz，根据式（6）～（9）给出涡轮所受轴向力和扭矩随时间变化规律，如图2 所示。压气机所受的扭矩与涡轮端大小相同方向相反，所受轴向力则为方向相反的恒定力。

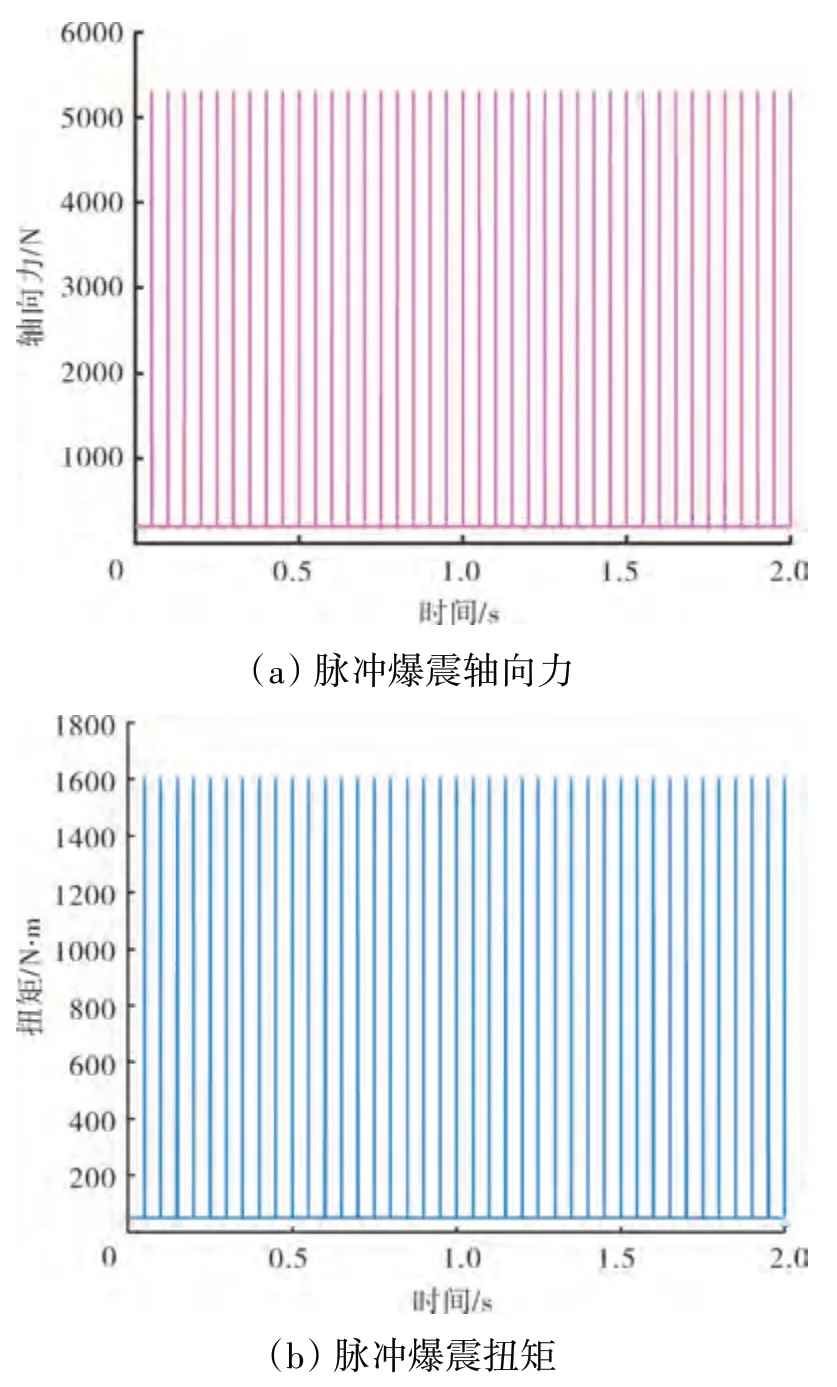
图2 涡轮所受轴向力和扭矩随时间变化规律

根据上述条件计算出转子的Campbell 图和频率响应特性，如图3、4 所示。从图中可见，转子转速在0～15000 r/min 内有多阶临界转速（正向同步涡动）且在靠近30000 r/min处存在第1阶临界转速。显然，转子的临界转速与发动机额定工作转速及慢车转速之间的安全裕度（避开率）不够。因此，需要进一步对其支承位置和刚度以及壁厚等参数进行优化。

图3 转子Campbell图

图4 转子幅频响应特性

基于优化策略，优化迭代完成后所得相关设计参数的值见表2。此外，优化后止推轴承的位置为距转子左端0.46 m。从表中可见，转子的壁厚经过优化减小至8 mm，这对降低转子的整体质量有益。采用优化后的转子参数进行动力学特性计算，得到改进转子的Campbell图和幅频响应曲线，如图5、6所示。

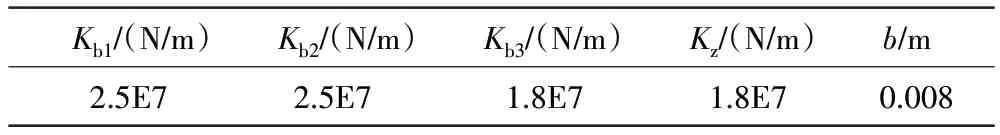
表2 优化后的设计变量

图5 优化后转子的Campbell图

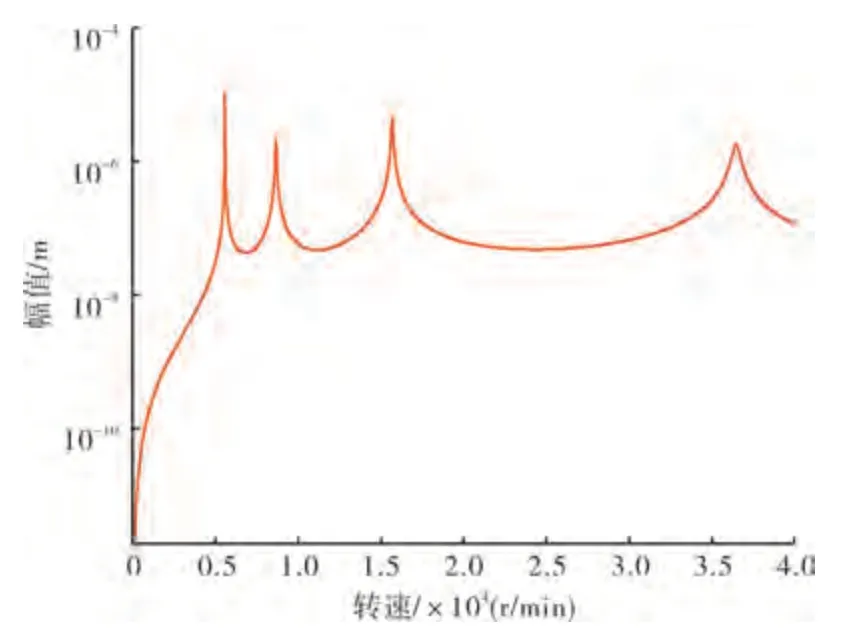
图6 优化后转子的幅频响应特性

从图中可见，优化后转子的临界转速分布比较均匀，前4 阶分别为5561、8644、15672 和36446 r/min。与慢车转速相邻的第2 阶临界转速的安全裕度分别为21.7%和21.6%，靠近工作转速的第4 阶临界转速的安全裕度为20.1%且数值上绝对转速差超过6000 r/min。在前4 阶临界转速范围内，转子的振幅均为10 μm 量级。由此可见，优化后的转子具有足够的安全裕度且各阶临界转速下其振动幅值已优化至最小化，在符合总体设计要求的同时控制了转子的振动幅值，确保了发动机的运行安全性。在优化设计过程中，根据设计需要和具备的计算资源可设置更多优化目标和选择更多的设计参数，确保设计方案满足各方面要求。