控制力矩陀螺微振动时的固有频率波动机理研究
2023-07-06朱泽昊周徐斌刘兴天冯彦军
朱泽昊,周徐斌,刘兴天,杜 冬,冯彦军
(1.上海卫星工程研究所;2.上海航天装备微振动环境模拟工程技术研究中心:上海 201109)
0 引言
控制力矩陀螺(CMG)是航天器姿态控制系统的重要执行机构,被广泛用于以高分辨率卫星[1]为代表的高精度航天器的姿态控制。近年来,在工程研制中常发生CMG 扰动引发蜂窝板等弹性支撑结构共振的问题,直接影响航天器姿控精度和相机工作,导致图像扭曲和模糊,并造成CMG 内部机械部件工作环境恶化。如何从CMG 的振动机理出发,指导地面试验进行不同工况的共振风险测试,以确保卫星在轨工作的可靠性,成为相关系统设计的关键问题之一。
为防止发生共振,设计CMG 时通常会避免宽频激励的频带范围覆盖其固有频率,然而在CMG旋转过程中其固有频率并非定值,因此存在发生设计外共振的风险。具体而言,CMG 是一个变结构系统,其内转子和框架的转动导致其固有频率存在不可忽视的波动范围,这使得其共振风险较传统结构明显增加。上海航天技术研究院近几年对多个遥感型号地面试验和在轨案例的分析也证明了上述情况。
CMG 的动力学研究是基于转子和陀螺的特性展开的。文献[2-4]通过理论建模深入研究了CMG的微振动扰动输出特性,但未对CMG 的本征特性进行具体分析。综合现有研究可知,CMG 固有频率波动的力学机理包括两方面:一是由于旋转机构带来的系统惯量变化和陀螺力矩方向的变化;二是由于不同柔性支承结构(如隔振器[4]、蜂窝板[5]、轴承非线性[6])导致的支承刚度变化。
CMG 的动力学地面试验与飞轮的类似。文献[7]阐述了刚性边界下,飞轮静止时(未考虑陀螺效应)安装界面处的加速度测量方法。文献[8-9]考虑陀螺效应的影响,设计了飞轮旋转时安装界面处的加速度测量方法。CMG 与飞轮最大的区别在于其框架角的变化会导致系统惯量和陀螺力矩方向发生变化,文献[10]研究得出在不同框架角下CMG微振动的响应幅值不同,但并未对CMG 的局部模态进行分析。文献[11]发现添加测力计导致CMG的一阶固有频率发生偏移,同时影响微振动响应,但没有分析框架角对固有频率的影响。总体来说,研究人员对CMG 固有频率变化与微振动特性的影响关注较少。
本文从CMG-蜂窝板组合体固有频率波动的机理出发,建立蜂窝板上CMG 的等效动力学模型,通过等效板理论和薄板理论求解蜂窝板刚度矩阵,结合CMG 工作时变化的惯量矩阵和陀螺矩阵,得到柔性界面CMG 系统的固有频率曲线,并分析其波动量的影响因素,提出CMG 设计优化策略,以期为CMG 地面试验设计提供理论指导,解决CMG 与蜂窝板共振问题。
1 数学模型建立
1.1 CMG-蜂窝板固有频率波动机理分析
CMG 作为典型的陀螺系统,含有两个旋转部件——高速转子系统和低速框架系统。在蜂窝板等柔性支承边界下,框架低速旋转改变CMG 的主惯量方向,转子高速旋转与蜂窝板的形变产生陀螺效应,从而改变CMG-蜂窝板组合体的固有频率。而组合体固有频率分析需要求解陀螺系统的二次特征值[12]问题,即
式中:M、K为对称的惯量矩阵和刚度矩阵,G为反对称的陀螺矩阵,皆为六阶实方阵,分别取决于CMG的质量特性和蜂窝板的刚度特性;λ和X分别为陀螺系统的特征值和特征向量,分别对应组合体的固有频率和振型。显然,M、K、G三者决定了CMG 的固有频率。下面对各系统矩阵进行详细建模。
1.2 CMG-蜂窝板动力学模型建立
1.2.1 相关假设与坐标系建立
柔性界面CMG 固定坐标系Ogxgygzg和蜂窝板面内坐标系Oxyz如图1 和图2 所示,首先假设:
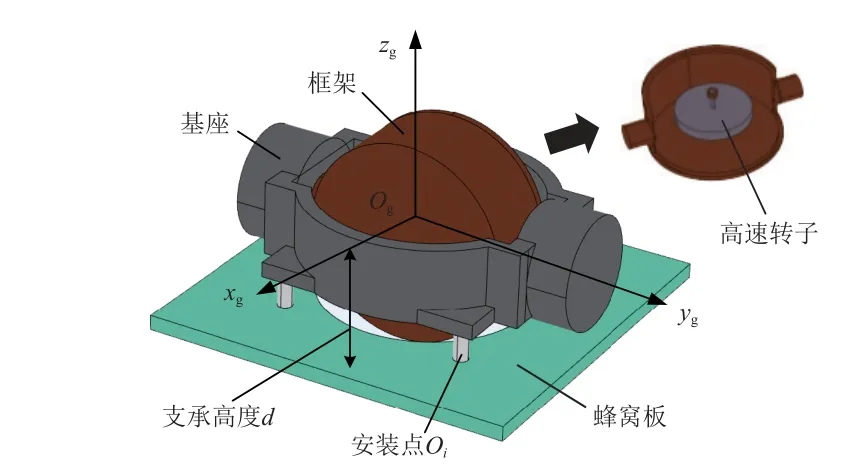
图1 柔性界面CMG 坐标系Fig.1 Coordinate of flexible interface CMG

图2 蜂窝板安装面坐标系Fig.2 Coordinate of honeycomb panel installation
1)CMG 的质量和惯量集中在其质心Og处,基座主惯量的方向不变,框架和转子的主惯量方向随框架旋转;
2)CMG 内转子的转速固定为Ω;
3)CMG 安装在长×宽×高为a×b×h的蜂窝板上,4 个固定安装点(记为Oi,i=1, 2, 3, 4)呈矩形分布(面积m×n),该矩形的中心与板的中心重合,CMG 质心Og的高度为d;
4)Og有6 个自由度,而由蜂窝板的性质可知Oi各有3 个平动自由度。
1.2.2 惯量矩阵和陀螺矩阵
在CMG 固定坐标系Ogxgygzg下,参考文献[4],采用一般形式的拉格朗日方程得到柔性支撑CMG 无阻尼自由振动的动力学方程
式中:
式(2)~式(6)中:xg为CMG 的平动和转动自由度;m为总质量矩阵;Jb为基座主惯量阵;Jg为框架(含转子)初始总主惯量阵;A为坐标转换阵;G0为初始陀螺矩阵;δ为框架角;Jp为转子轴向惯量。
分析式(3)、(4)可知,与转子固有频率的Cambell图[12]类似,CMG 的固有频率受到陀螺效应的影响而发生偏移,区别在于CMG 的框架绕y轴旋转,导致其主惯量阵和陀螺矩阵随框架角δ变化,且两矩阵在x、z方向交替变化,因此引起CMG 固有频率的周期性波动。可见,影响惯量阵的变量为框架角δ以及CMG 在x、z方向的初始主惯量比Jg1/Jg3,影响陀螺矩阵的变量为框架角δ、转子转速Ω和转子轴向惯量Jp。
1.2.3 蜂窝板刚度矩阵理论解
CMG-蜂窝板组合体的刚度矩阵K以仿真解为主,未见其数学模型以及理论解,而理论解在研究一般规律时有更好的效果。为得到组合体的等效刚度矩阵,采用柔度法计算刚度矩阵,即参考Hoff理论[13]将蜂窝板等效为各向同性板,在板的中心作用单位力(矩)矢量,得到柔度矩阵U,对其求逆即得刚度矩阵K=U-1。

1)薄板弯曲问题:在(xj,yj)作用集中力Zj,该问题有解析解,参考文献[15],薄板的挠度为
式中:Cps为满足力/位移边界条件的待定常数;k为挠度函数的阶数。由文献[15]得四边简支板的待定常数
式中D为薄板的弯曲刚度,D=Eh3/[12(1-μ2)],其中E和μ分别为薄板的杨氏模量和泊松比。
2)平面应力问题:在(xj,yj)作用集中力Xj、Yj,设面内位移方程为
式中,Aps、Bps为面内位移函数的待定系数,下面依照其边界条件进行求解。
将集中力用脉冲函数δ等效为体作用力,则有平面应力问题的平衡微分方程组


式(12)中:Fj=[XjYjZj]T,为各安装点的各向集中力;Uj=(xj,yj,zj),为各安装点的位移。
记板中心到安装点的矢量为Li=(ai,bi, 0),板中心位移为U0=(x0,y0,z0,α0,β0,γ0)T时,安装点位移为
式中Gi为位移传递矩阵,
则总位移传递矩阵为
其中,U=[U1U2U3U4]T,G=[G1G2G3G4]T。
同理,得到力的传递关系
式中:F0=(Fx0,Fy0,Fz0,Mα0,Mβ0,Mγ0)T,为作用在板中心的外力;F=[F1F2F3F4]T。
综合式(13)、(16)、(17)及刚度定义式F0=KU0,得总刚度矩阵
式(18)得到了CMG 质心与蜂窝板中心重合时刚度的解析解,并将蜂窝板等效为一个六阶解耦的弹性单元,当蜂窝板中心与CMG 质心的距离为d时,平动与转动刚度存在耦合,最终的刚度矩阵为
其中
根据上述分析,在蜂窝板材料、尺寸确定的情况下,CMG-蜂窝板组合体的刚度矩阵与CMG 的安装面积S=m×n、安装区域长宽比m/n以及质心高度d相关。
2 CMG 固有频率波动数值的仿真结果分析
2.1 模型正确性验证
将式(3)、式(4)与式(19)代入式(1)即可求解CMG-蜂窝板组合体的固有频率,为验证式(1)所得固有频率理论解的正确性,采用有限元软件模态分析进行对比,仿真参数的取值见表1。

表1 CMG-蜂窝板组合体仿真参数Table 1 Simulation parameters for CMG-honeycomb panel assembly
CMG-蜂窝板组合体的等效有限元模型如图3所示,蜂窝板等效为单层板单元,四边固支并通过4 个连接点与CMG 质心Og连接。组合体的4 种振型如图4 所示,其中(a)为绕y轴的弯曲模态,对应X/RY 模态;(b)为绕x轴的弯曲模态,对应Y/RX模态;(c)为沿z轴的线位移模态,对应Z 模态;(d)为绕z轴的扭转模态,对应RZ 模态。
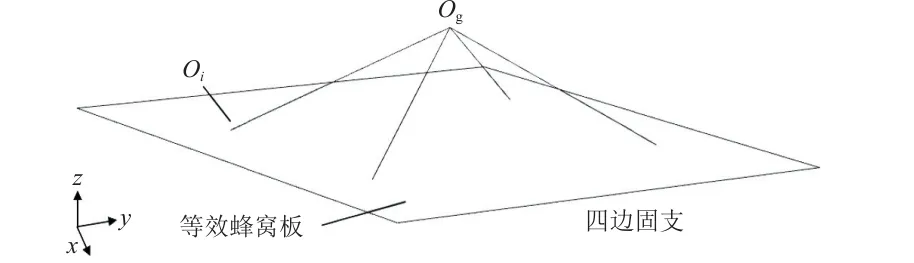
图3 CMG-蜂窝板组合体的有限元模型Fig.3 Finite element model of the CMG-honeycomb panel assembly
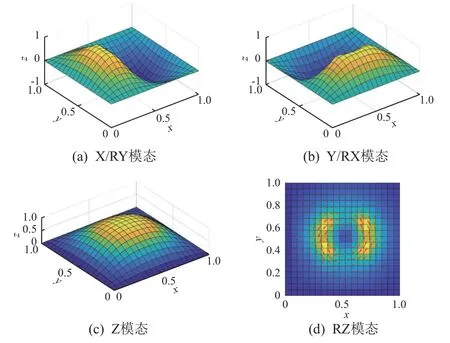
图4 CMG-蜂窝板组合体的振型Fig.4 Vibration mode of the CMG-honeycomb panel assembly
对比δ=0°、Ω=0 Hz 时CMG 固有频率的理论解和有限元解(如表2 所示),随着位移函数阶数k的增大,理论解与有限元解之间的偏差减小,当k=40时,最大偏差为RZ 模态的13.87%,其余模态的偏差都在10%以下,说明平面应力的求解方法收敛较慢,但可以见到其收敛趋势,故此理论解的正确性得到验证。
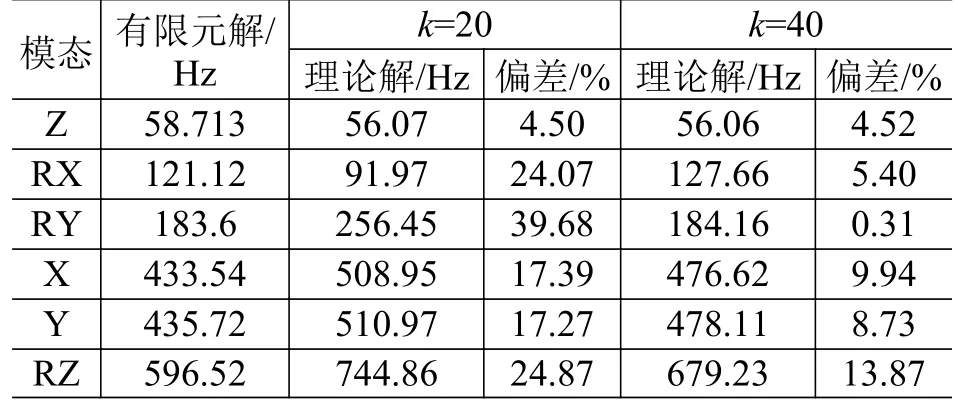
表2 固有频率的有限元解与理论解对比Table 2 Comparison between finite element solution and theoretical solution of natural frequency
2.2 等效刚度矩阵分析
蜂窝板的等效刚度矩阵与CMG 的安装面积S=m×n以及安装区域长宽比m/n相关。令S不变,m/n从0.1 到10 变化,板刚度曲线如图5 所示,当m/n→0.1, 10 时,安装区域退化为长梁,刚度显著增大;而当m/n处于0.2~5 的区间范围时,安装区域符合板的设定,刚度没有变化。
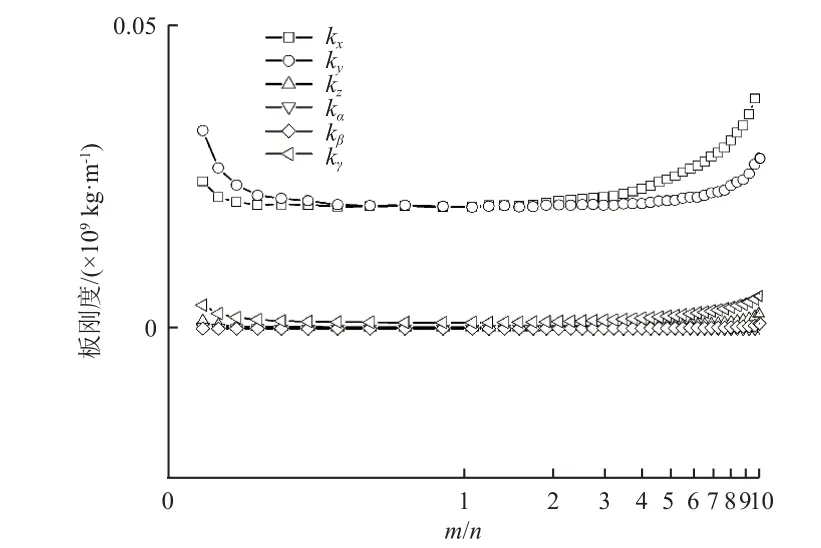
图5 板刚度与m/n 的关系Fig.5 Relationship between plate stiffness and m/n
令m/n=1.5 不变,改变S,板刚度曲线如图6 所示,图中的横坐标为安装面积比(S/(a×b))。可以看出,随着安装面积的增大,安装区域边界趋近板的边界时,板的刚度迅速增大;当安装区域边界无限靠近板边界时,板刚度无穷大。
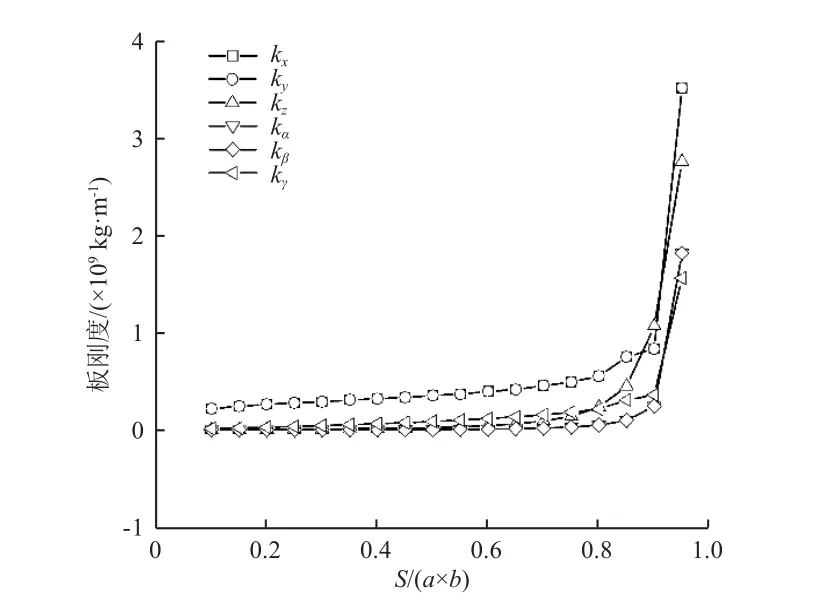
图6 板刚度与安装面积比的关系Fig.6 Relationship between plate stiffness and installation area ratio
上述分析说明,当CMG 安装在蜂窝板的中心,且其安装面积S固定时,安装区域的长宽比不影响板的刚度;安装区域面积越大(越接近边界),板的等效刚度越大。上述方法同样可用于计算载荷未安装在板的中心以及安装区域不规则的情况。
2.3 CMG 固有频率分析
CMG 安装于蜂窝板时,影响其固有频率的因素为框架角δ、CMG 质心高度d和转子转速Ω,最终表现形式为其模态耦合,如表3 所示:质量矩阵使得RZ、RX 惯量耦合,刚度矩阵分别使RX、Y 和RY、X 的平动与转动刚度耦合,陀螺矩阵使得3 个转动自由度互相耦合。

表3 CMG 的模态耦合情况Table 3 Modal coupling of CMG
由于 CMG 系统矩阵的耦合情况很复杂,下面分几种情况进行讨论。
1)只考虑刚度耦合,即δ=0,Ω=0,d≠0
如图7 所示,改变CMG 的安装高度d,则x、y向的转动刚度与平动刚度耦合,使得RY、RX 自由度的固有频率降低,x、y自由度的固有频率增加,此时RX、RY 频率可能与转子转速Ω的扰动力共振。
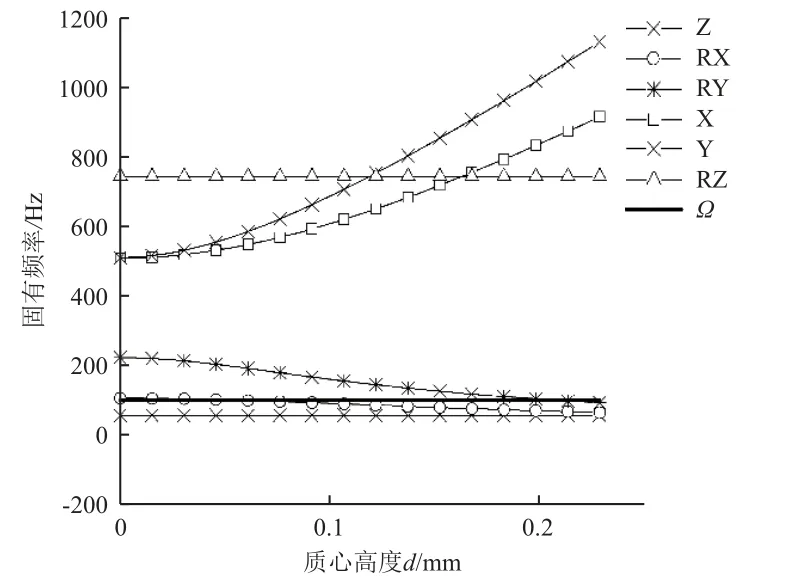
图7 CMG 固有频率随其质心高度的变化Fig.7 Variation of natural frequency with height of center-ofmass
2)不考虑刚度耦合,即δ≠0,Ω≠0,d=0
当d=0 时刚度矩阵为对角阵,图8 为CMG 位于δ=0°位置时,其固有频率随转子转速Ω变化的Cambell 图,其中RX、RY 模态为正反进动曲线,由于RX 模态频率与Ω在100 Hz 附近有交点,存在共振危险。图9 为转子转速为Ω=100 Hz 时,不同框架角δ下CMG 框架旋转时六阶固有频率的周期性波动情况,可以看到,此时RX、RY、RZ 模态频率都发生了频率波动,由式(3)、(4)可知RX、RZ 的频率波动来源于x、z方向惯量的交替变化,而RY的波动量来源于增加的陀螺矩阵。
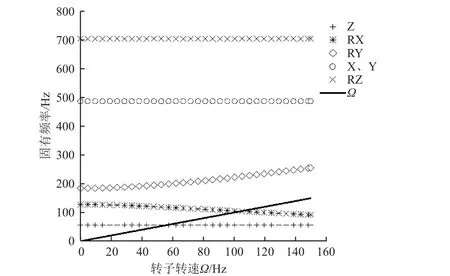
图8 CMG 固有频率随转子转速Ω 变化的Campbell 图(δ=0°)Fig.8 Campbell plot of CMG natural frequency varying with rotor speed Ω (δ=0°)

图9 CMG 固有频率随框架角δ 的变化Fig.9 Natural frequency varying with frame angle δ
2.4 CMG 共振频带分析
由于CMG 框架和转子的旋转导致惯量方向和陀螺力矩方向改变,两者共同作用使得CMG 的固有频率发生复杂的变化。图10 为转子升速到100 Hz时,CMG 固有频率随框架角变化的包络曲线,阴影区域即为在固定转角下,转子升速时CMG 固有频率的变化量。令df1为阴影区域的最大长度,df2为该频率的波动宽度,两者分别表征δ、Ω引起频率波动的频带大小。将两者除以δ=0、Ω=0 时的基频f0,得到无量纲参数分别表征δ、Ω引起i(i=X, Y, Z, RX, RY, RZ)阶模态频率波动的频带大小。
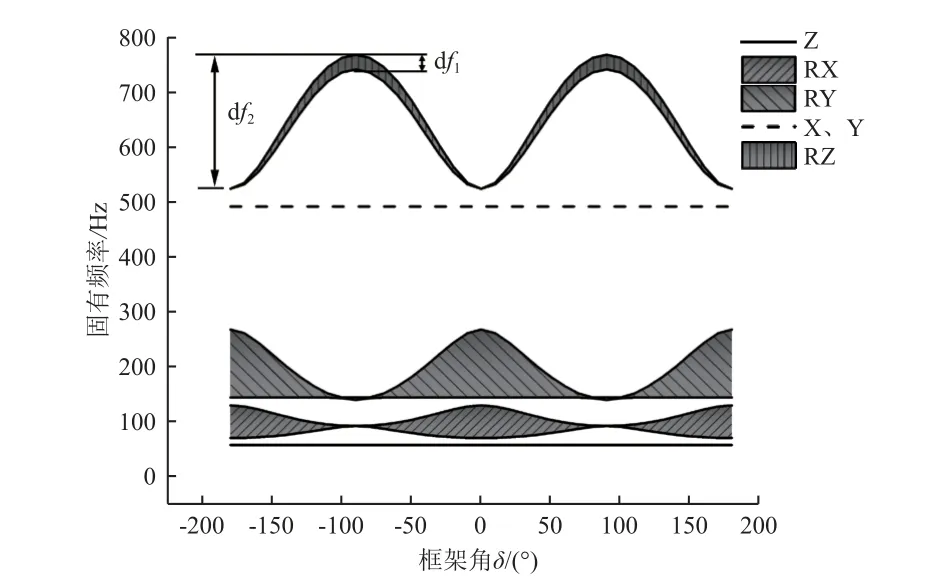
图10 不同角度下CMG 固有频率包络(Ωmax=100 Hz)Fig.10 Natural frequency envelope of CMG at different angles (Ωmax=100 Hz)
当转子轴向惯量Jp从0 增加到1 kg·m2时,如图11 所示,令纵坐标为相对波动量riI,横坐标为转子惯量与CMG 同方向惯量的比值Jp/Jg3。由图可知,与Jp/Jg3成正比,即转子惯量增加时陀螺效应变强,这是转子系统所共有的特性。
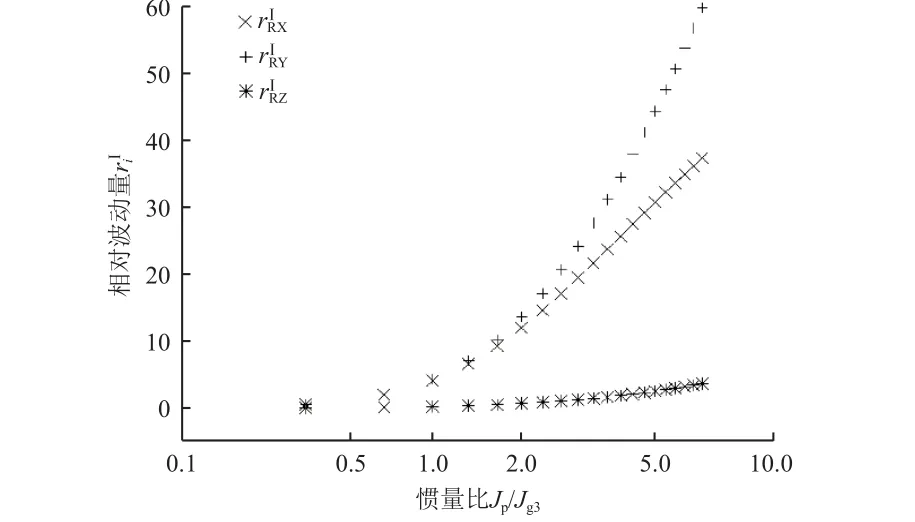
图11相对波动量riI的变化规律Fig.11 Changepatternof relativefluctuation variable riI
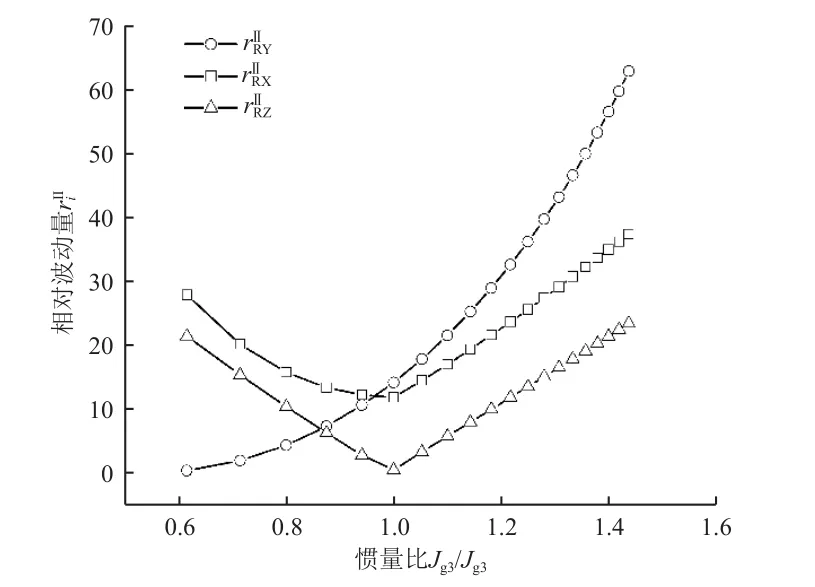
图12 相对波动量riII 的变化规律Fig.12 Change pattern of relative fluctuation variable riII
3 结论及建议
本文建立了蜂窝板上CMG 的动力学模型,分析了导致CMG 固有频率波动的多方面因素,得到结论如下:1)CMG 的安装面积比越大,CMG-蜂窝板组合体的等效刚度越大。2)CMG 的安装高度越高、转子转速越快,由于刚度耦合以及陀螺效应引起的固有频率偏移越大;3)转子轴向惯量相对框架同方向的惯量越大,陀螺效应对CMG 固有频率的影响越大;4)框架惯量交替变换引起CMG 固有频率周期性波动,且交替变换的两个惯量差值越大,波动量越大。
基于上述分析结果提出对应设计建议:1)CMG的安装区域应接近蜂窝板边界,以确保达至尽可能高的界面刚度;2)适当降低CMG 的安装高度和转子转速,以确保组合体固有频率的偏移量在可接受的范围;3)在保证转子惯量Jp满足姿轨控的角动量需求基础上,通过适当增大框架沿转子轴的惯量Jg3,可以有效减弱陀螺力矩对CMG 固有频率的影响。4)令框架惯量Jg3与Jg1(Jg2为电机轴惯量)接近,可以减小惯量变化引起的固有频率波动。
同时,上述分析对CMG 的地面试验也有指导作用,体现在:1)CMG 的固有频率在其工作过程中是一个变值,对其进行准确测量较为困难,因此先基于理论分析得到CMG 固有频率再进行微振动测试可以简化试验流程;2)通过CMG 固有频率的理论分析结果对扫频试验时的共振频率进行预测,有助于对其结构模态进行充分辨识,从而制定更有效的振动抑制策略。
本文主要基于已有的地面试验和在轨测试现象进行理论分析,条件具备时将对文中研究内容进行专门的验证试验。
