高强钢管混凝土的耐火极限

刘 晓, 贺海阳, 杨 佳, 回彦川,2, 王 杰

(1. 沈阳大学 a. 建筑工程学院, b. 沈阳市民用建筑智慧防灾减灾重点实验室, 辽宁 沈阳 110044;2. 武汉大学 土木建筑工程学院, 湖北 武汉 430072)

高强钢一般指屈服强度超过460 MPa的钢材,在钢管混凝土的基础上改变钢材强度就成了高强钢管混凝土。钢管混凝土(concrete-filled steel tube, CFST)构件是指在钢管中填充混凝土而形成的组合构件。按截面形式的不同可以分为矩形截面、圆形截面和多边形截面钢管混凝士结构,其中圆形截面和矩形截面钢管混凝士结构应用较为广泛[1]。火灾下,钢材的材料性质会随着表面温度的不断升高而逐渐劣化,而核心混凝土一方面可以吸收来自外钢管的热量使其升温滞后,另一方面可以承担外钢管卸载下来的载荷。当钢管混凝土柱承受的载荷相同时,采用高强钢管比采用普通钢管更能提高耐火极限。

国内外的专家学者对钢管混凝土均匀受火的耐火极限进行了一系列的研究:李坤等[2]对影响钢管混凝土柱耐火极限的各项参数进行了分析;侯景军[3]建立了轴心受压钢管混凝土柱有限元模型,并分析了柱的长度、钢材屈服强度、柱截面尺寸等参数对构件耐火极限的影响;宋天诣等[4]对不同组合结构的耐火极限研究成果进行了归纳,并进行了深层次的研究和展望;王志滨等[5]研究了异形钢管混凝土柱的耐火极限,同时分析了截面形状、保护层厚度和保护层种类等参数对耐火极限的影响。

本文利用ABAQUS有限元软件对高强钢管混凝土的耐火极限进行模拟,分析混凝土强度、钢材屈服强度、载荷比和外钢管壁厚等对火灾下高强钢管混凝土耐火性能的影响。

1 有限元模型建立

采用相继热力耦合的方法,运用ABAQUS软件建立高强钢管混凝土构件的有限元分析模型。先对钢管和核心混凝土选择合适的热工参数,建立正确的温度场模型,再选择高温下钢材和混凝土的本构关系,最后将温度场得到的节点温度导入到力场模型的预定义场中进行耐火极限的计算。

1.1 温度场建立

本文致力于研究火灾下高强钢管混凝土的耐火极限,首先需要建立温度场模型,通过比对国内外学者关于温度场的研究,最终选择Lie等[6]提出的温度场热工模型来建立温度场。火灾模型选取ISO-834标准升温曲线。

建模时核心混凝土和盖板采用实体单元,外钢管采用壳体单元,壳体厚度用9个辛普森积分点提高计算的准确性。高强钢管混凝土柱网格划分如图1(b)～图1(d)所示,分析步设为热传递,钢管外表面考虑热对流和热辐射,参考欧洲规范的建议,受火面对流换热系数为25 W·(m2·k)-1;综合辐射系数为0.5;玻尔兹曼常数为5.67×10-8W·(m2·k4)-1; 钢管与混凝土之间采用绑定约束,钢管与端板采用壳与实体单元接触[7]。钢管采用4节点壳单元, 混凝土和盖板采用8节点实体单元。

在预定义场中

整个模型选择初始温度为20 ℃,温度场中热辐射和热对流的布置参考图1(a)。

1.2 应力场建立

应力场模型可以先把温度场复制后进行修改,这里面的核心步骤是把温度场输出的文件导入预定义场中。温度场的分析步时间要和应力场一致,保证整个受火阶段的温度都要导入,最后通过加载点的位移来计算它的耐火极限。在建立应力场模型时可以参考文献[8]的设置,即外钢管和混凝土的相互作用由法线方向的硬接触和切线方向的库伦摩擦模型构成,其中摩擦系数取为0.6较合适。划分网格要和温度场模型保持一致,所有的部件单元类型设置为3维应力。

为了让计算更符合工程实际,选择合适的应力-应变本构关系模型显得尤为重要。高强钢管混凝土柱在火灾下的耐火极限计算主要经历常温和升温2个阶段,下面是2个阶段的本构模型。

1) 常温阶段。常温阶段的钢材本构可以参考韩林海[9]提出的双折线模型。由于高强钢材在常温阶段无明显屈服平台,因此采用如图2的应力-应变关系保证此模型具有较好的计算精度。核心混凝土在常温阶段采用韩林海[9]提出的约束混凝土的应力-应变模型(20 ℃),而钢管与混凝土之间的相互作用关系可以通过约束效应系数来考虑。

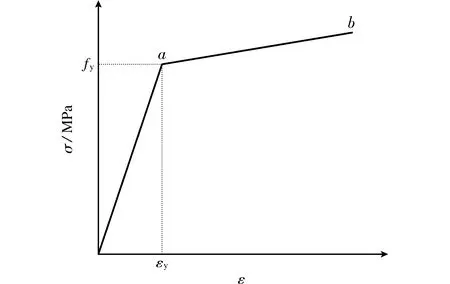
图2 钢材的应力应变关系曲线Fig.2 Stress-strain relationship curves of steel

2) 升温阶段。在这一阶段,文献[10]中高温下的钢材应力-应变模型效果更为明显,能够顺利模拟出钢材在火灾下的力学性能。其中钢材的泊松比基本不随温度变化,其值为0.3。升温阶段下的核心混凝土本构模型参考韩林海[9]提出的约束混凝土应力-应变模型。

2 模型验证

利用ABAQUS对于文献[11-12]中的试件进行模拟,建立相应的温度场和耐火极限模型,分别验证模型的正确性。试件主要参数如表1,其中:Bo为外钢管的直径;to为外钢管的壁厚;L为柱高;fyo为钢材的屈服强度;fcu为混凝土立方体抗压强度;N为施加在试验构件上的固定载荷;n为载荷比;tr为耐火极限试验值;t为通过有限元模拟计算得到的耐火极限值。

表1 试件参数Table 1 The parameters of the specimen

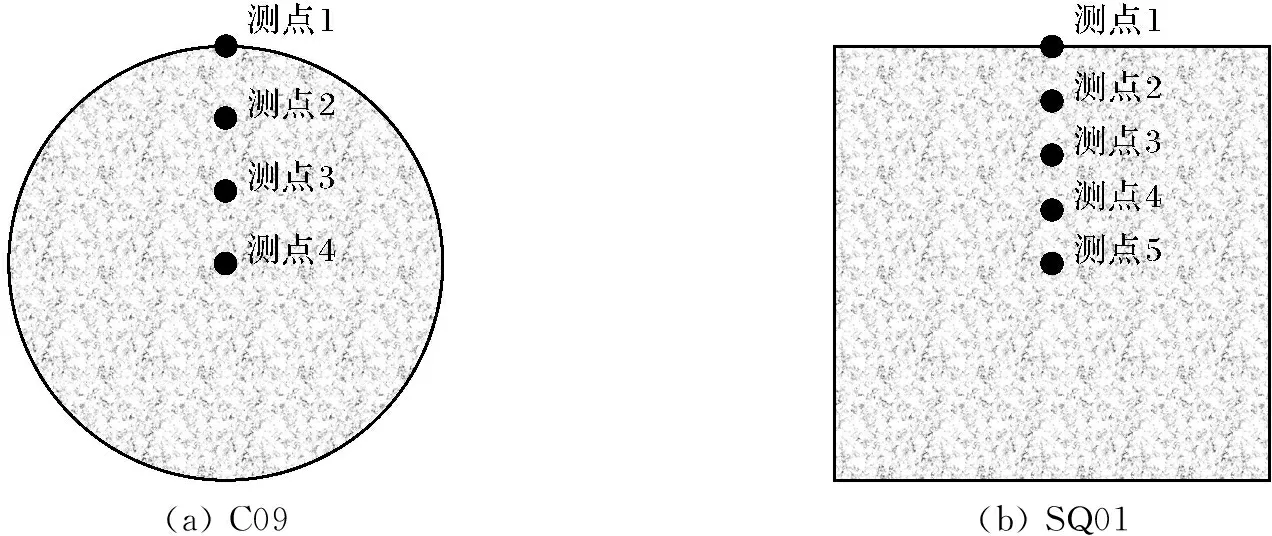
对表1试件C09和SQ01分别进行温度场分析,图3是高强钢管混凝土柱截面形状的测点,图3(a)中测点1是钢管外表面,测点4是混凝土内部中心点,测点2和测点3均匀分布在测点1和测点4之间。图3(b)中5个测点将钢管外表面到中心点的距离均匀分成4份。图4为温度场试验测点、曲线与建模计算对比,由图4可见,用ABAQUS模拟得到的温度测点-时间曲线与试验测得的温度测点-时间曲线比较接近,所以可以用ABAQUS来模拟试件的温度场。

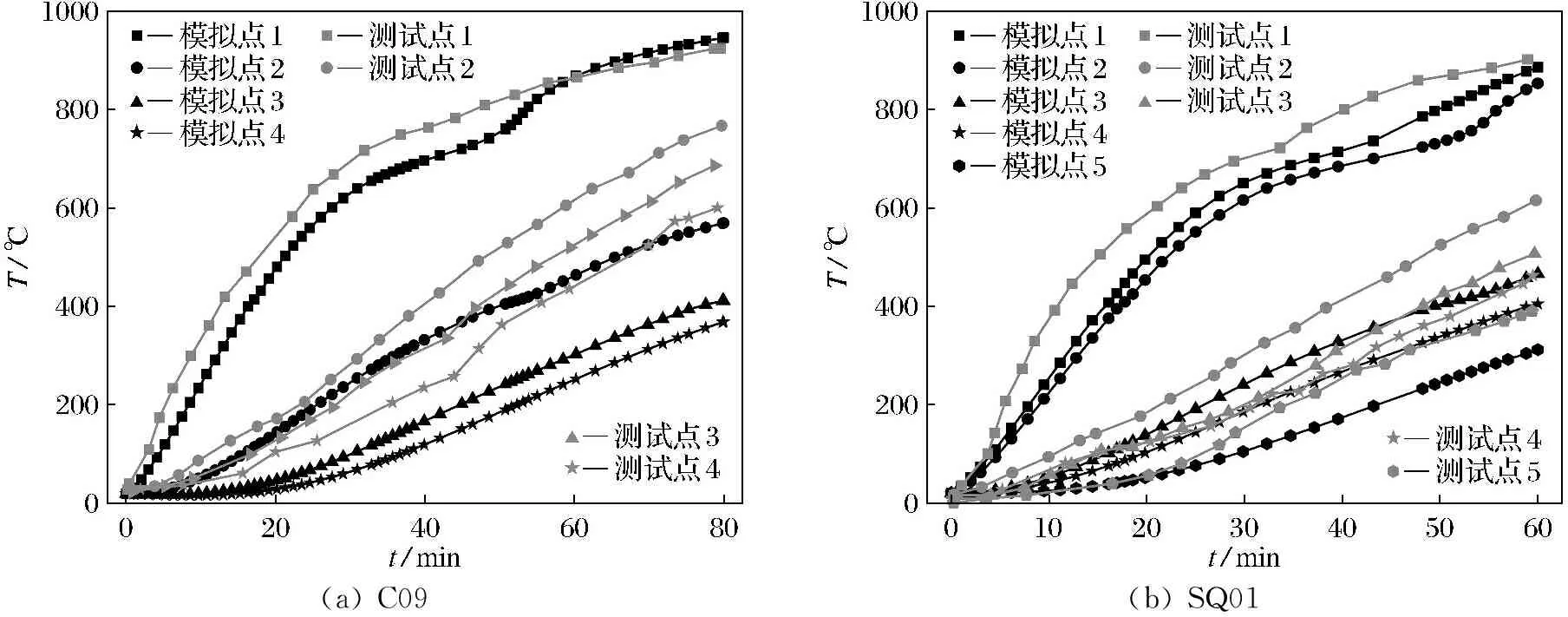
图3 高强钢管混凝土柱截面形状的测点Fig.3 Point measurement of the cross-sectional shape of high-strength steel pipe concrete column

图4 温度场试验测点曲线与建模计算对比Fig.4 Comparison of the temperature field test point curve with the modeling calculation

对表1中4个试件进行耐火极限建模分析计算,图5所示为钢管混凝土柱耐火极限实测结果与模拟结果的对比情况,从中可以看出4个试件都比较吻合,C09前期的膨胀较大,曲线开始下降的时间也比较晚,但是整体来看大体趋势较为相似。S7和S10前期膨胀得早,后期曲线下降得也早。模拟得到的耐火极限与试验值二者比值的平均值为1.01,均方差为0.01,可见二者总体上相差不大,所以可以用ABAQUS来模拟试件的耐火极限。

(a) C09(b) SQ01

3 温度场分析

以1根柱长为1 m的圆形钢管混凝土柱为例进行温度场分析,钢材屈服强度为460 MPa,核心混凝土抗压强度为30 MPa。外钢管直径为200 mm,壁厚为3 mm,升温时间是180 min。对构件进行截面温度分析,其中测点1是钢管外表面,测点3是内部混凝土中心的点,测点2在测点1和测点3中间。根据图6可知钢管混凝土前期温度升高较快,后期温度升高逐渐变慢。从位置来看,测点1温度高于测点2,测点2温度又高于测点3,可见测点温度随着距离钢管外表面的加大而降低。

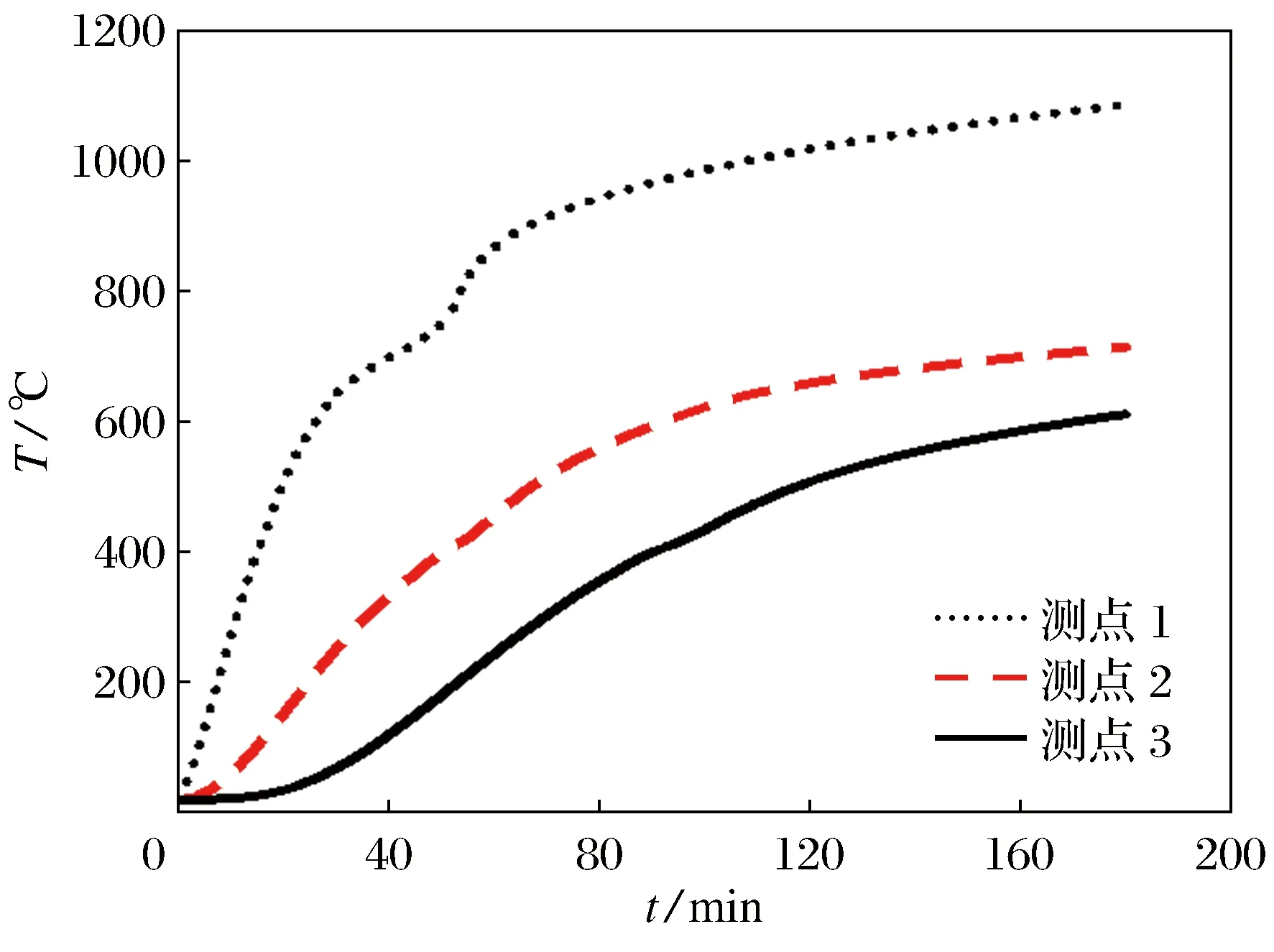
图6 柱截面不同测点的受火时间温度曲线

图7为混凝土截面温度场分布趋势,由图7可知,从混凝土外侧到中间点温度先均匀降低后下降速度逐渐变慢,混凝土最高温度1 088 ℃、最低温度612 ℃。温度从外到内逐渐降低,一方面是因为混凝土吸热,另一方面也受到混凝土中水蒸气的影响。

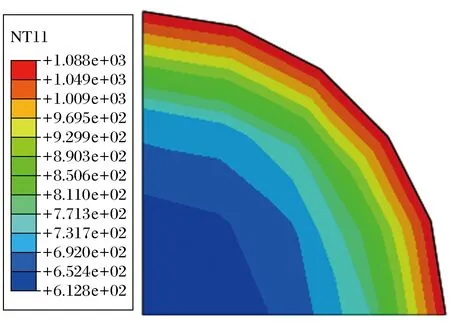
图7 混凝土截面温度场分布趋势

4 参数分析

火灾下均匀受火的高强钢管混凝土柱的耐火极限受钢材屈服强度fy、混凝土抗压强度fcu、载荷比n、外钢管壁厚to等参数的影响。有限元模型参数如表2所示。

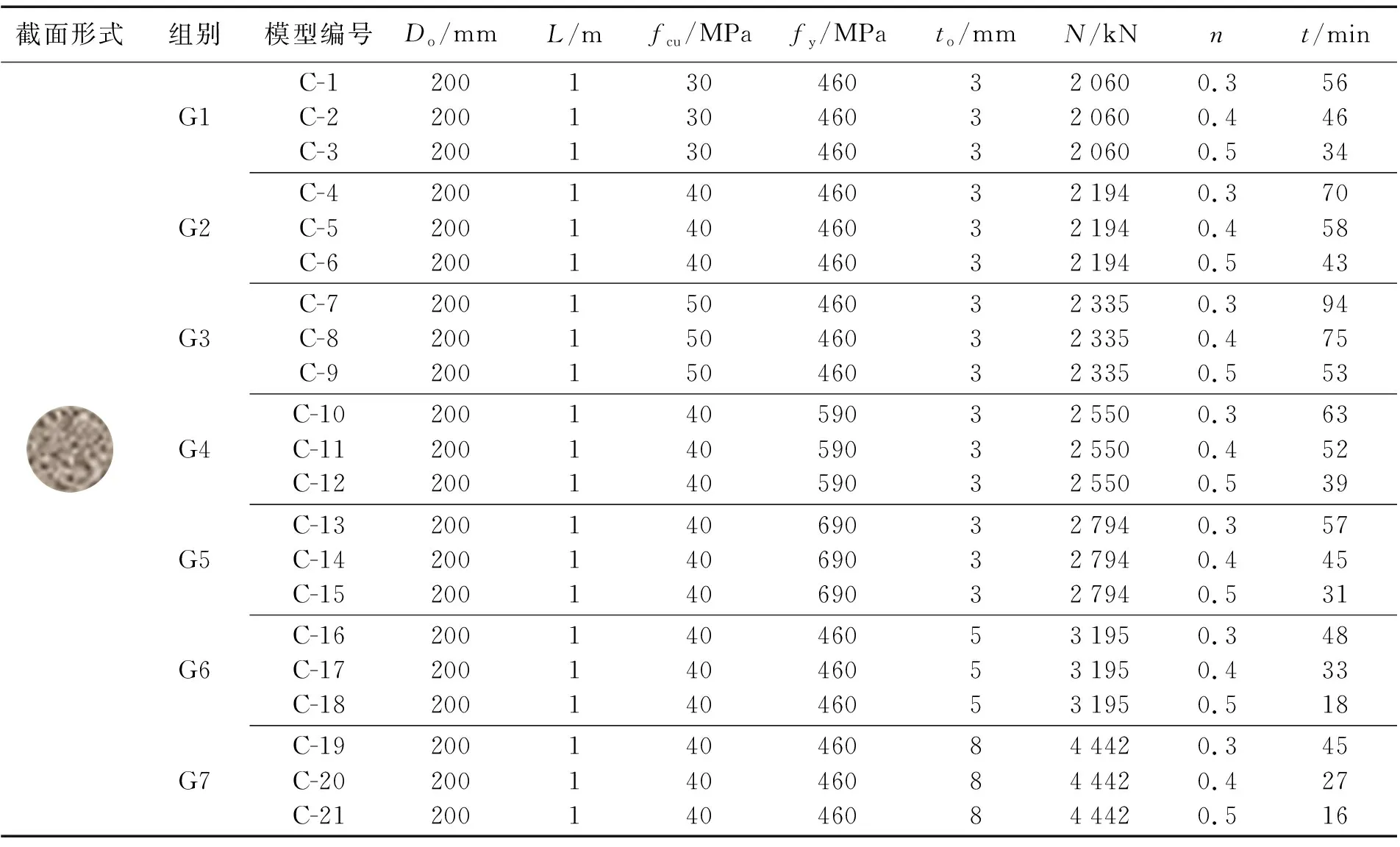
表2 有限元模型参数Table 2 Finite element model parameters

4.1 混凝土抗压强度

对G1、G2、G3等3组模型进行对比分析,来研究不同混凝土抗压强度对耐火极限的影响。不同混凝土抗压强度对耐火极限的影响如图8所示。当载荷比为0.3时,从30 MPa到40 MPa再到50 MPa耐火极限分别增加25%和34%;当载荷比为0.4时,耐火极限分别提高26.1%和29.3%;当载荷比为0.5时,耐火极限分别提高26.4%和23.2%。研究发现,当其他参数不变而仅改变混凝土强度时,耐火极限数值呈递增趋势,即随混凝土抗压强度的不断增加而增加。一方面,核心混凝土强度变化也会影响极限承载力数值,即随核心混凝土强度的提高,常温下构件的极限承载力数值分别增加了6.5%和6.4%,可见核心混凝土强度的提高对常温极限承载力贡献极小;另一方面,随着核心混凝土强度的提高,构件可以承受更多钢管卸载的载荷。因此,通过提高核心混凝土的抗压强度也可以提高耐火极限,并且效果比较明显。

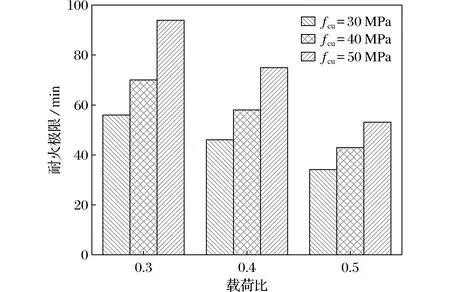
图8 不同混凝土抗压强度对耐火极限的影响Fig.8 The effect of different concrete compressive strengths on fire resistance limits

4.2 钢材屈服强度

对G2、G4、G5等3组模型进行对比分析,来研究钢材屈服强度对耐火极限的影响。不同钢材屈服强度对耐火极限的影响曲线如图9所示。研究发现当只改变钢材的屈服强度而保持其他参数不变时,耐火极限数值呈降低趋势,即随钢材的屈服强度的升高而降低。屈服强度数值从460 MPa升至590 MPa和690 MPa时:当载荷比为0.3时,耐火极限分别下降了9.5%和10%;当载荷比为0.4时,耐火极限分别下降10.3%、13.5%;当载荷比为0.5时,耐火极限分别下降9.3%、20.5%。分析发现,随着钢材屈服强度的增加,高强钢管混凝土的极限承载力分别增加了16.2%和9.5%。可以看出,钢材屈服强度对常温下试件的极限承载力有很大影响。在相同载荷比的火灾情况下试件会受到更大的载荷,钢材屈服强度的增加变相增加了作用在核心混凝土上的载荷。所以钢材屈服强度与耐火极限成反比,增加钢材屈服强度反而会降低耐火极限,并且随着钢材屈服强度的提高耐火极限的下降趋势会逐渐变大。

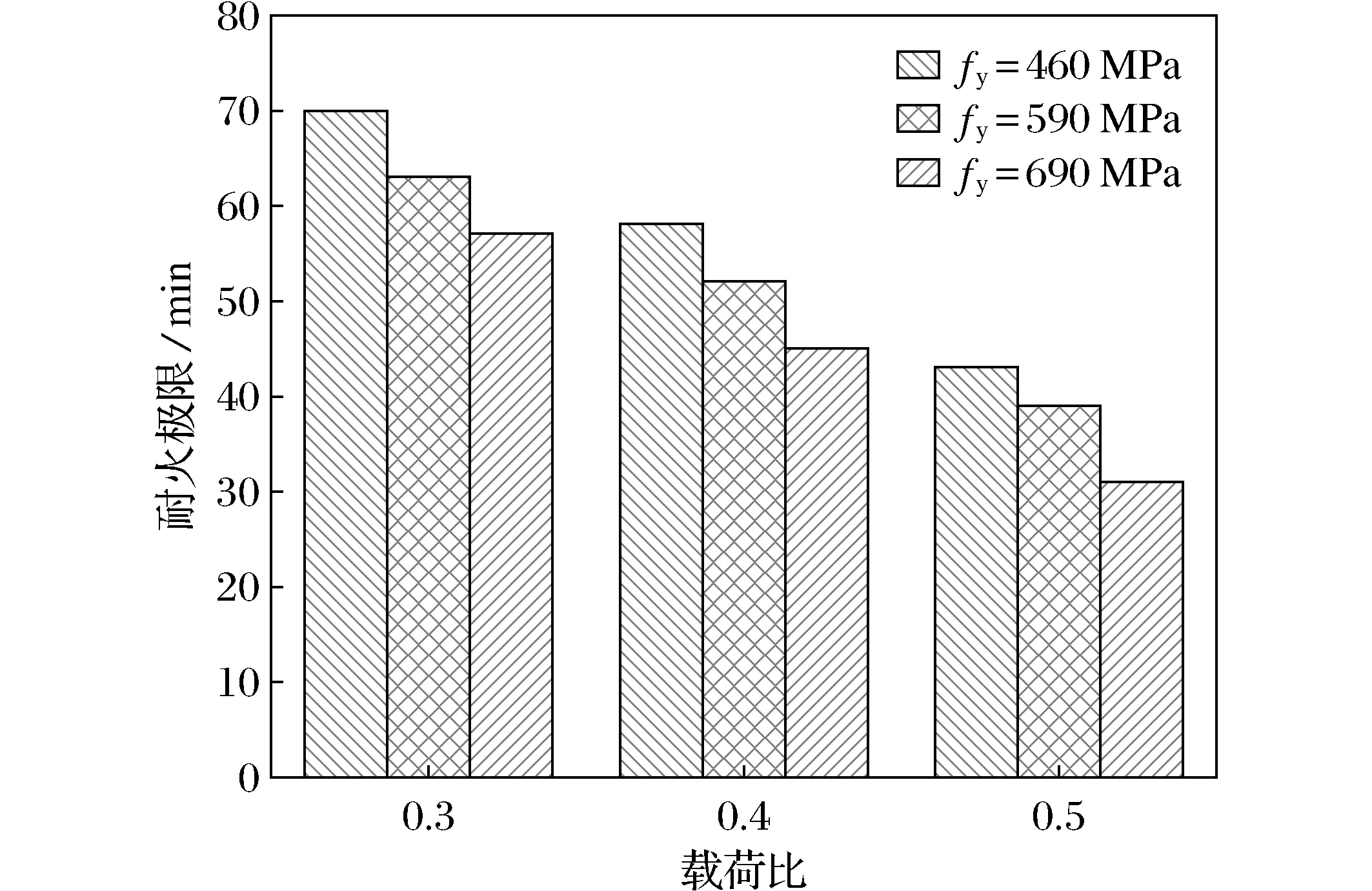
图9 不同钢材屈服强度对耐火极限的影响Fig.9 The effect of the yield strength of different steels on the limit of fire resistance

4.3 载荷比

载荷比是火灾下高强钢管混凝土柱受到的恒定载荷与常温下受到的极限承载力的比值。对G1、G2、G3等3组高强钢管混凝土模型进行对比分析,不同载荷比对耐火极限的影响如图10所示。当混凝土抗压强度为30 MPa,载荷比从0.3到0.4再到0.5时耐火极限分别下降17.8%、26.0%;当混凝土抗压强度为40 MPa时,载荷比从0.3到0.4再到0.5时耐火极限分别下降17.1%、25.5%;当混凝土抗压强度为50 MPa时,载荷比从0.3到0.4再到0.5时耐火极限分别下降20.2%、29.3%。研究发现,耐火极限随载荷比的增加而降低,因为随着载荷比的增大,作用在受火构件上的载荷也增加,构件达到耐火极限所需的时间减少。

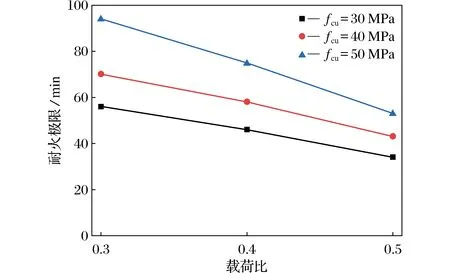
图10 不同载荷比对耐火极限的影响Fig.10 The effect of different load ratios on the limits of fire resistance

4.4 外钢管壁厚

对G2、G6、G7等3组高强钢管混凝土模型进行分析,外钢管壁厚选用3 mm、5 mm、8 mm等3种,不同外钢管壁厚对耐火极限的影响曲线如图11所示。外钢管壁厚从3 mm到5 mm再到8 mm时:当载荷比为0.3时,耐火极限分别下降31.4%、6.3%;当载荷比为0.4时,耐火极限分别下降41.3%、62.5%;当载荷比为0.5时,耐火极限分别下降58.1%、11.1%。

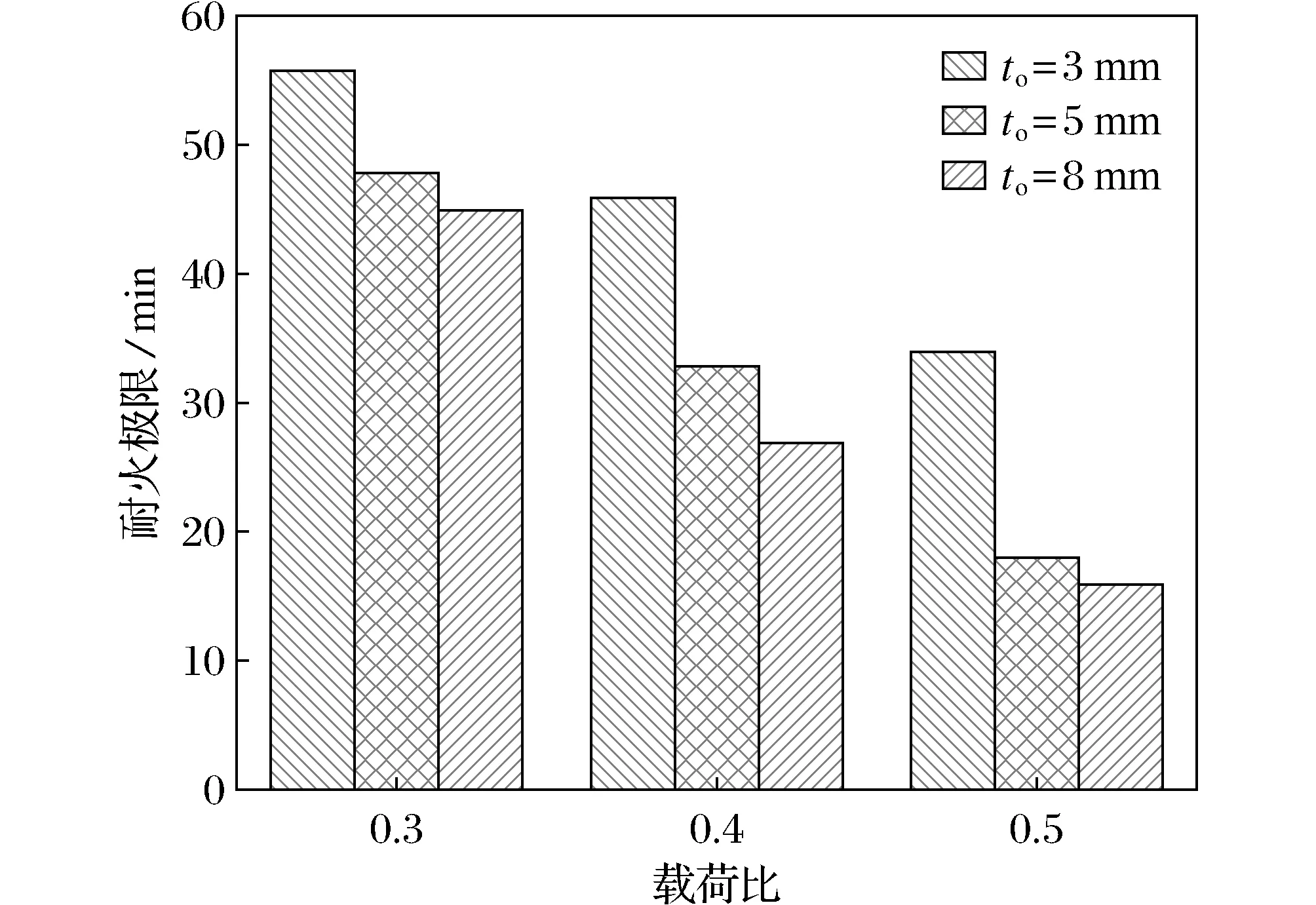
图11 不同外钢管壁厚下的耐火极限Fig.11 The limit of fire resistance under different outer steel pipe wall thicknesses

5 结 论

建立了高强钢管混凝土耐火极限有限元模型,对比试验结果验证了该模型的正确性。得到结论如下:

1) 耐火极限数值会随核心混凝土抗压强度的不断增大而增大。核心混凝土抗压强度的增加对常温下试件的极限承载力影响不大,但对耐火极限有显著影响;

2) 耐火极限与钢材屈服强度成反比,增加钢材屈服强度反而会降低耐火极限;

3) 耐火性能随载荷比的增大而大幅度降低,由此表明载荷比是影响高强钢管混凝土柱耐火性能的主要参数;

4) 在同一载荷下,高强钢管混凝土在耐火极限方面要优于普通钢管混凝土。