基于改进ShuffleNetV2的织物颜色恒常性算法

杨必成, 张团善

(西安工程大学 机电工程学院, 陕西 西安 710048)

近年来,随着工业生产效率的不断提高,人们对织物的颜色有了越来越高的要求。以前,织物之间的色差都是由专业的师傅肉眼进行辨别,但是由于长时间工作产生的视觉疲劳的影响,织物的色差检验准确率较低[1-2]。为了提升检验的准确率,机器视觉被引入织物的色差检验中,然而由于工业生产环境复杂,不同的灯光颜色以及明暗程度都会对织物产生一定的色偏,进而影响色差的检验效果。

移除不同光照颜色带来的色偏称为计算颜色恒常性。计算颜色恒常性的目标是模拟人类视觉系统在不同光照下对物体颜色的感知能力保持不变的特性。随着人工智能的发展,计算颜色恒常性为计算机视觉下游任务提供了稳定的颜色特征,例如:目标检测、3维重建等。因此,颜色恒常性在计算机视觉中扮演着越来越重要的角色。

目前,计算颜色恒常性的方法分为2类:基于统计的方法和基于学习的方法。最经典的统计算法是灰度世界算法(gray-world),该算法假设世界上的颜色都趋向于中性灰色,因此,光照颜色可以被估计为输入图像的平均颜色。随后,在此基础上又提出了灰色阴影算法(shade of grey)和灰色边缘算法(grey-edge)。这类算法是高效、快速、敏捷的,但由于是利用像素统计和物理特征来估计场景中的光照且对于光照反射的分布统计过于简化,因而很难去处理复杂世界的复杂场景。随着机器学习和深度学习的不断发展,基于学习的颜色恒常性算法在性能方面得到了很大的提高。Barron等[3]提出了快速傅里叶颜色恒常性,这个算法是把颜色恒常性问题转化为环面上的空间定位问题,通过频域操作,性能得到了很大的提高,可以作为一种精确、实时的自动白平衡算法。Hu[4]等提出了带有置信度加权池的全卷积颜色恒常性算法,该模型会自适应地给予每个patch局部位置不同的权重来进行端对端的训练,解决了某些patch可能包含信息模糊的问题,从而实现了更高的效率和准确性。Banic[5]等提出了基于学习的无监督的颜色恒常性模型,模型在逼近训练图像的未知真实地面光照后学习其参数值,避免了校准。McDonagh[6]等把相机自适应颜色恒常性问题视为少镜头的元学习问题,利用色温的概念进行少样本的回归任务,可以快速适应之前看过的相机。Afify等[7-14]在颜色恒常性方面做出了很大的贡献,利用基于U-Net的多输入多输出网络结构提出了跨相机卷积颜色恒常性,这个模型可以生成卷积颜色恒常性的权重从而动态的适应不同的相机,同时挑战传统的单帧时域颜色恒常性算法,通过取景器中的多帧来完成光照颜色的估计。最近,Tang等[15]使用统计方法与迁移学习相结合的思想,把数据集处理为与相机无关的情况,从而实现了跨相机颜色恒常性。Zhou[16]等为了消除场景光照对染色织物色差评价的影响,提出了一种基于极限学习机和灰狼优化器-蚁狮优化器的染色织物光照校正算法。另外,Zhou[17]等针对印染环境中光源的不稳定会引起织物表面颜色的变化,造成严重的色差评价误差问题,提出了一种基于正则化随机向量函数链接网络的染色织物光照估计方法。Liu[18]等针对染色织物易受光线变化影响,影响染色织物色差分类正确性的颜色特性,提出了基于改进海洋捕食者算法优化随机向量函数链的染色织物色恒度计算方法。后来,Liu[19]等为了解决现有照明估计方法在图像恢复时精度不高的问题,提出了一种基于鲸鱼优化算法的随机向量函数链接照明估计算法。以上这些基于学习的方法相较于基于统计的方法,在准确性方面有很大的提高,也可以去处理复杂世界中的场景。但是,由于计算量和参数量较大,在速度、推理方面较慢,不适合部署到计算机资源有限的移动终端上。

因此,本文提出了一种基于改进ShuffleNetV2的织物颜色恒常性算法。这个算法以ShuffleNetV2的框架为基础[20-21],使用H-Sigmoid激活函数代替ReLU激活函数,引入通道注意力机制[22]。在公共数据集上的结果表明,本文提出的算法可以有效地消除图像中的色偏,而且在织物的颜色校正上短时间内也能取得很好的效果。

1 基于改进ShuffleNetV2的织物颜色恒常性算法

1.1 Lambertian成像模型

在RGB颜色空间中,物体表面一点的颜色与相机、物体表面、光照有关,图像成像模型如下:

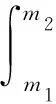
(1)

式中:x表示RGB空间中的坐标;λ表示可见光的波长;[m1,m2]表示可见光谱,可见光波长范围为380～780 nm;g(x)表示实际获取的图片;E(λ)表示光源光谱分布;R(x,λ)表示物体表面x处在标准白光照射下的光谱反射率;C(λ)表示相机传感器的感光特性函数。

如果在图像采集的过程中,场景中只有一种光源,那么光照颜色只与光源的光谱分布和相机的感光特性函数有关,那么光照颜色可表示为

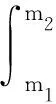
(2)

式中,e代表的是光照颜色向量。

1.2 对角模型

与VonKries模型类似,在2种不同光照下,同一相机拍摄出来的同一场景的图片可以由对角乘积来互相转换。可以表示为

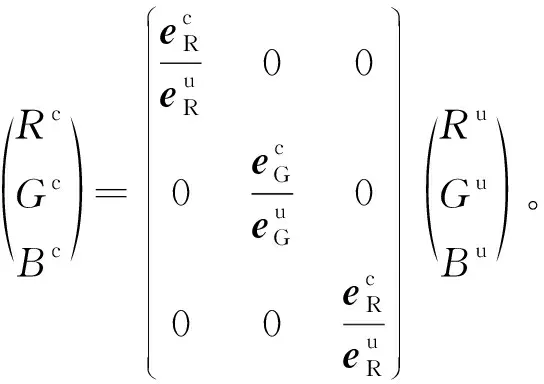
(3)

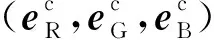
1.3 网络模型构建

由对角模型可知,颜色恒常性问题的解决需要估计出场景光源的颜色。神经网络可以学习一个函数来估计出光源的颜色,可表示为

ec=f(I)。

(4)

式中:ec表示光源颜色;I表示输入图片;f(I)表示构建的神经网络。

1.4 改进ShuffleNetV2的颜色恒常性算法

为了充分提取关于光照的颜色特征并解决部署在计算资源有限的移动终端的算法适配性不强的问题,提出了基于改进ShuffleNetV2的颜色恒常性算法,该算法的整体网络框架如图1所示(见封2)。本文算法首先对数据集进行预处理,将预处理后的图片传入改进的ShuffleNetV2结构进行特征提取,提取出的特征经过6×6×64以及1×1×4两个卷积层后得到4维特征层,第1维特征层为confidence(置信度),剩余3维特征层为estimation(估计)。然后通过对提取的特征进行置信度加权以获得更多的用于光照估计的特征从而准确地估计出光源,最终,用估计出来的光源来矫正带有色偏的图片,从而获得标准光源下的图片。

1.5 改进的ShuffleNetV2单元结构

ShffleNetV2网络的框架是根据4条轻量化网络设计准则进行搭建的:1)输入输出通道数相同时,内存访问量MAC(内存访问成本)最小;2)分组数过大的分组卷积会增加MAC;3)碎片化操作对并行加速不友好;4)逐元素操作(element-wise)带来的内存访问和耗时不可忽略。根据这4条准则设计出的ShffleNetV2网络单元结构如图2所示。

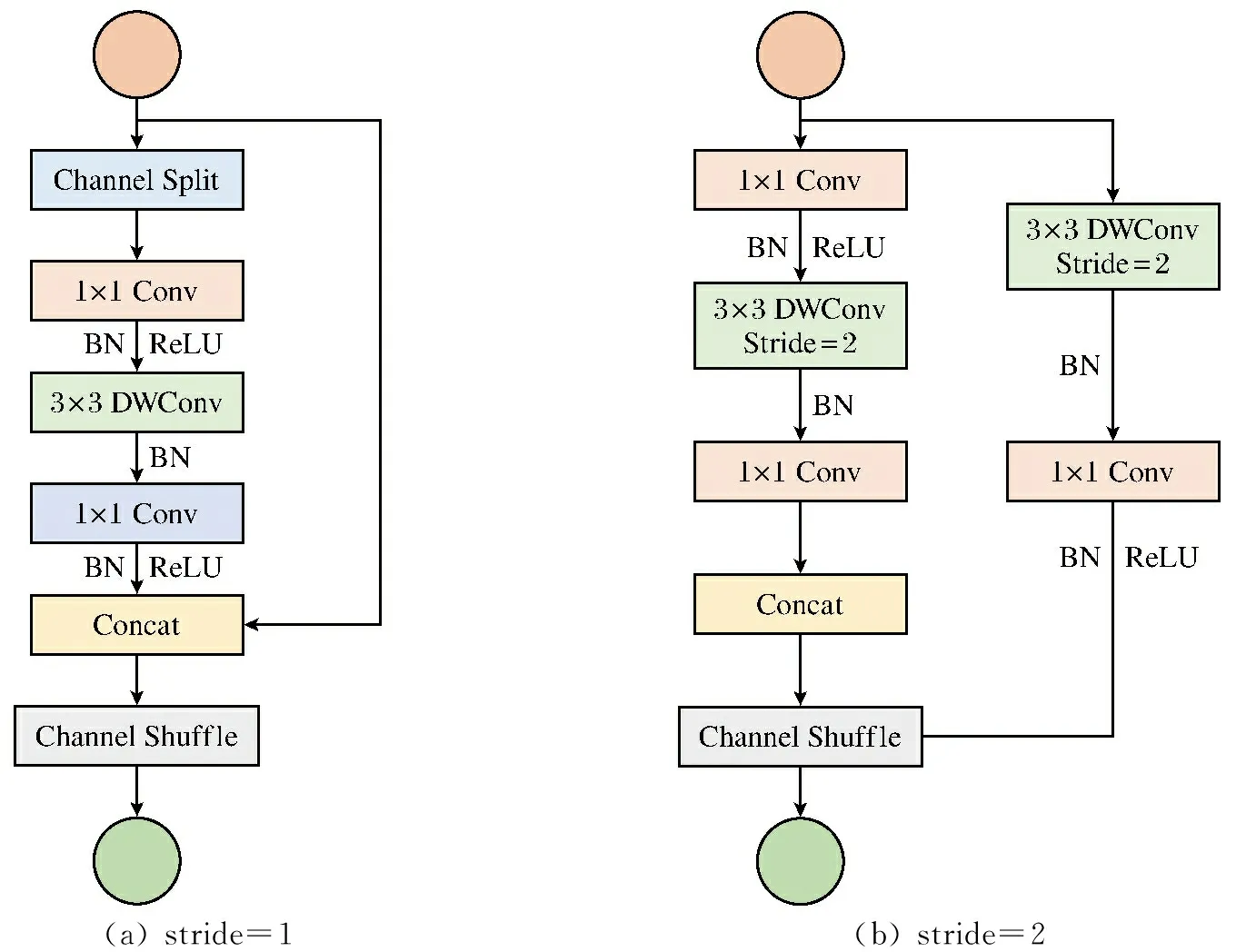
(a) stride=1(b) stride=2

在图2(a)的单元结构(下称a单元结构)中,首先对输入的特征图进行Channel Split(特征层在通道维度划分),把输入特征图的维度分给左、右分支各一半,左分支的经过Channel Split后保持不变;右分支通过3个卷积,分别为步距为1的1×1的普通卷积,3×3的DWConv(深度可分离卷积),1×1的Conv(普通卷积);左右分支的结果通过Concat连接(特征层在通道数维度进行拼接),最终通过Channel Shuffle(通道重洗)使得通道之间的信息充分融合。在图2(b)的单元结构(下称b单元结构)中,一开始没有进行Channel Split,左分支通过步距为2的3×3的深度可分离卷积之后,紧接着经过1×1的普通卷积;右分支通过2个1×1的普通卷积、1个3×3的步距为2的深度可分离卷积。最后通过Channel Shuffle来实现不同组之间的信息融合。

a单元结构左分支从1×1的分组卷积换为1×1的普通卷积满足了准则2分组数过大的分组卷积会增加MAC;右分支没有进行任何操作满足了准则3碎片化程度对并行加速不友好;最后用Concat代替Add(特征层在各自维度进行相加)以及ReLU(激活函数)放在Concat之上满足了准则4的逐元素操作会增加内存访问;左右分支输入输出的Channel数相同满足了准则1的条件。b单元结构同样也满足4条准则。ShuffleNetV2的单元结构设计大大加速了网络的推理速度,适合部署在计算机资源有限的移动终端上。

如图3所示,ShuffleNetV2 0.5x网络结构的输入图片大小为3×224×224,经过卷积核大小为3×3、步距为2的普通卷积后得到24×112×112的特征图,紧接着是卷积核大小为3×3、步距为2的最大池化层得到24×56×56的特征图,然后通过Stage2、Stage3、Stage4。每个Stage都是由ShuffleNetV2的a单元结构以及ShuffleNetV2的b单元结构组成,每个Stage中a单元结构以及b单元结构的重复次数的比例分别为1:3、1:7、1:3。最后,通过1×1的普通卷积以及全局池化层来防止过拟合,提高网络的泛化能力。

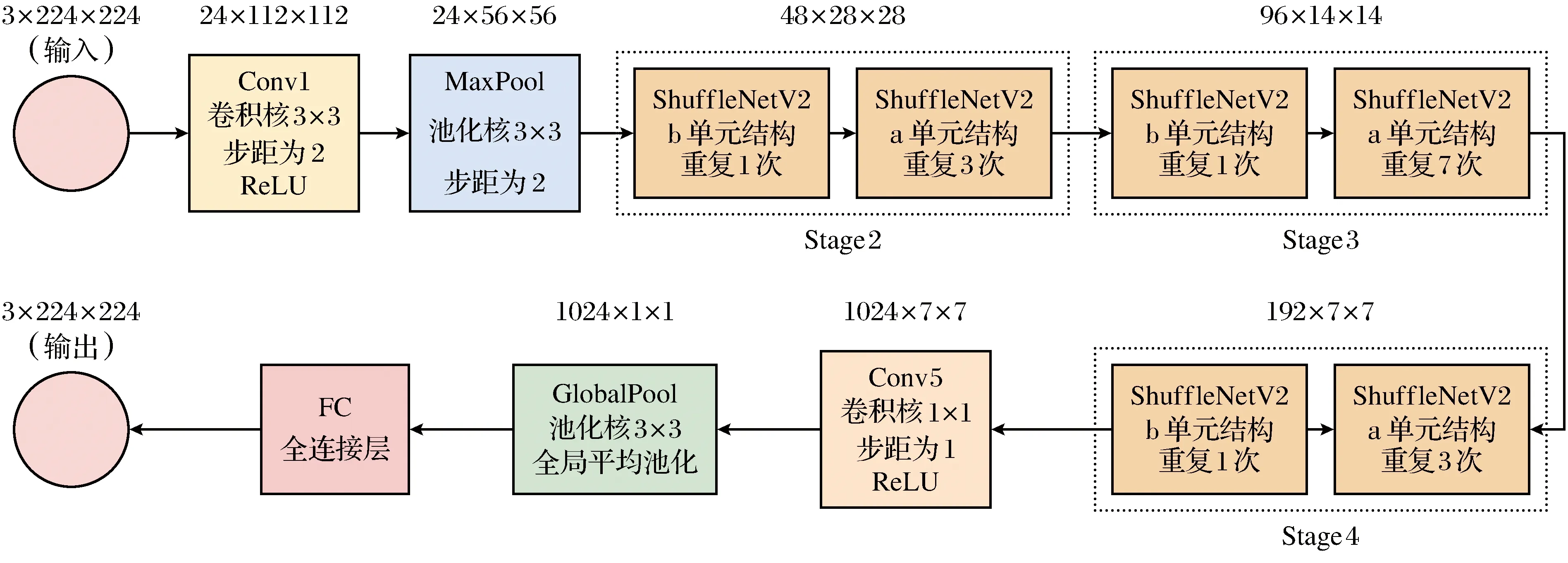
图3 ShuffleNetV2网络结构Fig.3 ShuffleNetV2 network structure

图4为改进后的ShuffleNetV2网络结构图。与分类网络不同的是,颜色恒常性网络结构不需要提取特别复杂的特征信息,仅仅需要中层语义信息。因此,去除Stage4模块,并且把Stage2、Stage3中a单元结构与b单元结构的Repeat的次数比例分别调整为1∶1。同时在每个Stage的ShuffleNetV2单元结构中添加ECA注意力机制模块,来关注明暗、颜色等特征信息。在Conv1中使用H-Sigmoid激活函数代替ReLU激活函数,使得网络结构深度降低的同时仍然可以保证网络的性能。改进的ShuffleNetV2结构经过2个卷积层后得到一个4维特征层,第1维为置信度,剩余3维为估计,置信度与估计进行加权后使得图片的不同局部区域具有不同的权重,进而更加准确的估计出光照颜色。

图4 改进的ShuffleNetV2网络结构Fig.4 Improved ShuffleNetV2 network structure

1.6 ECA注意力机制模块

颜色恒常性网络结构主要是为了进行光照估计,因而提取颜色特征是很关键的。通道注意力机制主要关注的是明暗、颜色等特征,空间注意力机制主要关注的是空间中的某部分物体,因此在网络中增加通道注意力机制可以更好的提取颜色特征。常用的通道注意力机制有ECA和SE。ECA通道注意力机制相当于是SE通道注意力机制的改进版本,它是一种轻量的通道注意力机制模块,模型复杂度小。SE注意力机制对输入的特征图进行了通道压缩,而这样的压缩对学习通道之间的依赖关系有不利影响。其次,SE注意力机制模块捕获所有通道的依赖关系,因而是低效的。ECA注意力机制避免降维,使用一个1D卷积代替原来的全连接层,实现了跨通道信息的获取,提高了通道之间的依赖关系。

ECA注意力机制首先对特征图进行全局平均池化,其次进行卷积核大小为k的1维卷积操作,并使用sigmoid激活函数得到各个通道的权重。权重与原始输入特征图对应元素的乘积得到最终的输出特征图,如图5所示。其中卷积核的大小是根据通道系数自适应选择,公式如下:

图5 ECA注意力机制模块Fig.5 ECA attention mechanism module

(5)

式中:ksize是指卷积核大小;b与Cgamma都是常量,分别等于1和2;a表示通道个数。

2 实验结果与分析

本文的实验环境为英特尔i5CPU,GPU为NVIDIA GeForce RTX3080,12GB显存,操作系统为Ubuntu 20.02的64位系统。本文所提网络是在Python3.7.2、Pytorch1.9.1下搭建的。实验中采用Adam优化器进行网络反向传播的优化,使用余弦淬火学习率进行网络的迭代训练。

2.1 数据集以及预处理

为了验证本文算法的有效性,实验采用Gehler-shi和NUS-8两个常用的颜色恒常性算法公共数据集。Gehler-shi数据集[23]是最经典的1个数据集,它包含室内和室外的场景图片共568张,这些图片分别是由Cannon 1D和Cannon 5D相机进行捕捉得到。NUS-8数据集[24]一共有1 736张图片,该数据集中的图片是由8个相机进行捕捉得到,每张图片包含用于提供光源真实颜色的颜色检查器,进行网络训练的时候,这部分被遮盖。

数据集图片传入神经网络之前需要进行预处理,预处理方式有随机裁剪、去马赛克、去饱和度等一些操作,从而进一步加速网络的推理过程,提高网络的泛化能力。

2.2 角度误差以及性能指标

为了更加准确地估计出光源颜色,得到近乎标准光源下的图片,采用角度误差函数作为网络训练过程中的损失函数。

(6)

为了评估算法的性能,从角度误差的均值、中值、三均值、最好25%、最差25%等5个指标来进行评估。

表1的角度误差统计结果表明,在Gehler-shi数据集上,本文算法在中值、均值、三均值指标上都有最优的结果,在最好25%、最差25%指标上有着竞争性的结果,表明本文算法性能不错。表2的角度误差统计结果表明,在NUS数据集上,本文算法在均值、最好25%、最差25%指标上有着最优的结果,在均值与中值指标上有着竞争性的结果,表明本文算法在面对复杂环境时稳健性以及鲁棒性较好,因此可以处理复杂世界的复杂场景。

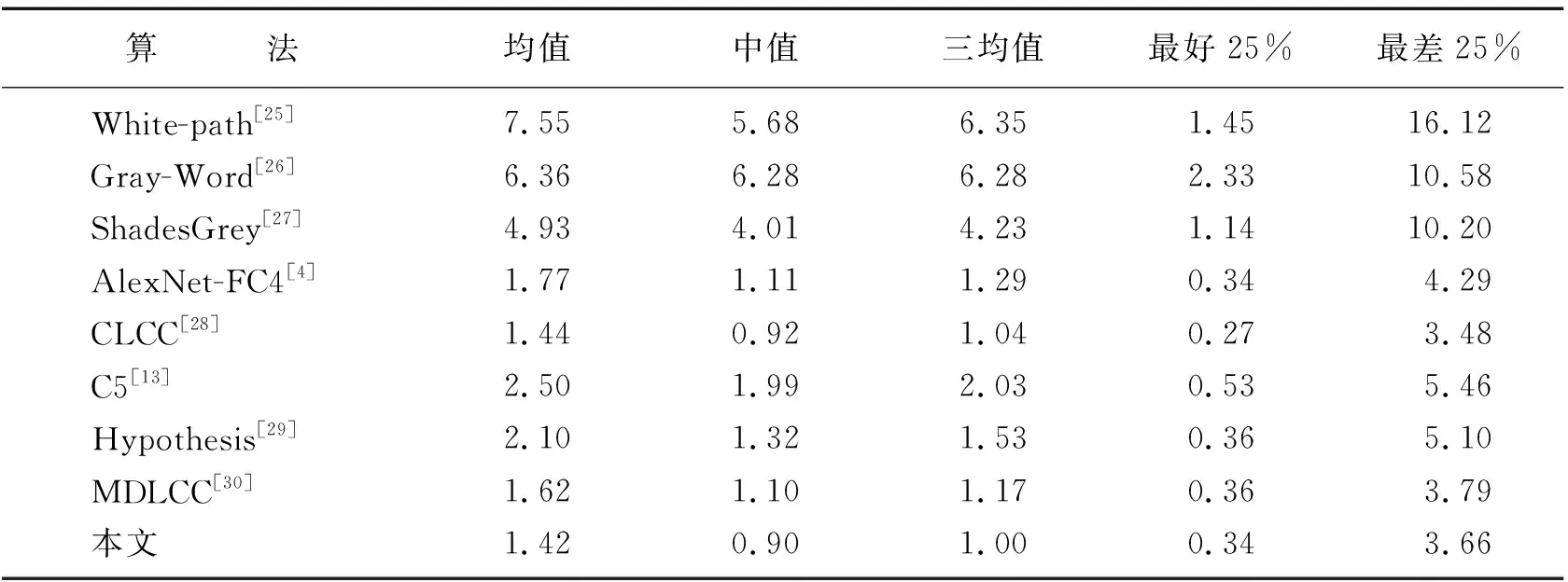
表1 Gehler-shi数据集上角度误差统计结果Table1 Statistical results of angle error on Gehler-shi dataset

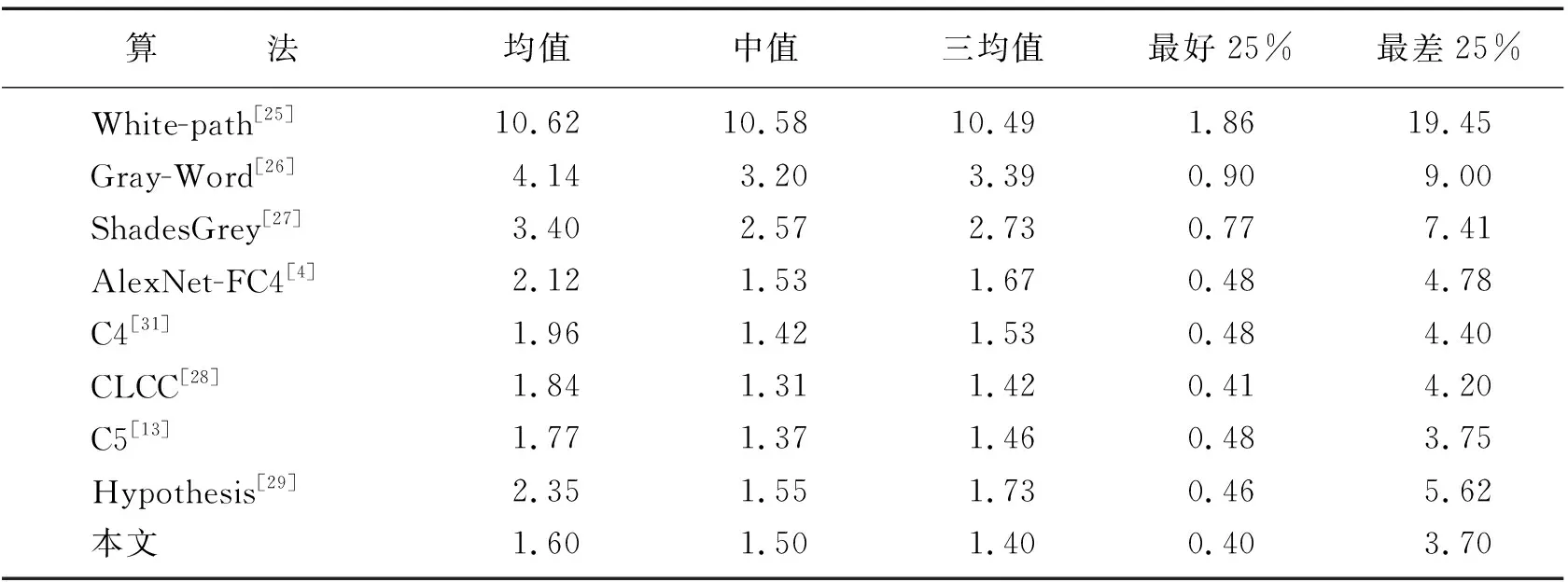
表2 NUS数据集角度误差统计结果Table 2 Statistical results of angle error on NUS dataset

表3的实验结果表明,不同的基于学习的颜色恒常性算法模型复杂度不同,因此,每个模型的参数量不同,一般情况而言,参数量越大,FLOPs(计算量)就越大,从而网络推理每张图片所用时间不同。从实验结果可以看出,本文的算法的参数量最少,因而间接表明网络的推理速度最快,测试一张图片大约需要0.02 s,满足了部署在资源有限的移动终端的性能要求。

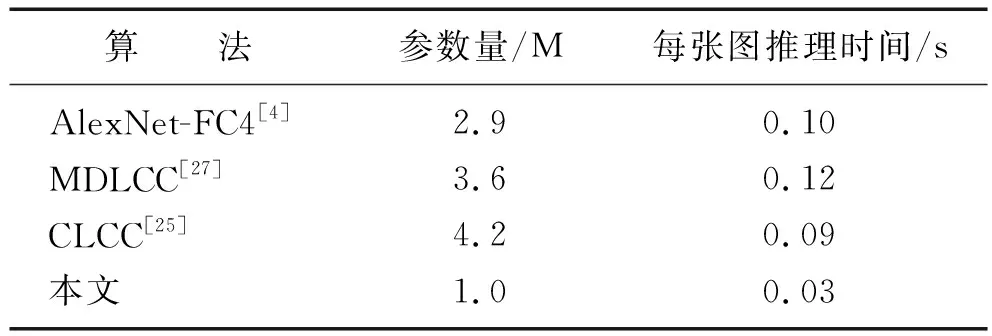
表3 不同算法之间的复杂度对比Table 3 Complexity comparison between different algorithm

2.3 织物的颜色校正

实验平台主要是由电脑、 相机、 光源、 传送带、 可调节支架、 织物等装置组成, 如图6所示。 电脑是i5CPU,GPU为NVIDIA GeForce MX250,2GB显存; 相机选择迈德威视公司的MV-LD-25-5M-K工业镜头, 焦距为0

1—电脑; 2—光源; 3—布匹; 4—传送带; 5—相机; 6—可调支架。图6 织物颜色校正平台Fig.6 Fabric color correction platform

通过调节红、绿、蓝LED光源的亮度为25%、50%、75%及100%的不同比例,得到了不同颜色的光源,如品红色光源、黄色光源等。在这些光源照射的同时,右侧上方也安装了1个标准的白色光源进行照射,以避免室内场景的一些光源亮度不足对实验结果的影响。采集了不同光照下的织物数据集,以在公共数据集上训练的的算法权重作为预训练权重,来训练织物的颜色恒常性网络,其流程如图7所示。实验结果表明,所采集的织物数据集经过本文算法的校正后得到了近似标准光源下照射的织物的结果。

图7 训练流程Fig.7 Training flowchart

NUS数据集的可视化结果如图8所示(见封2)。

图9为织物的颜色校正可视化结果(见封3)。实验结果表明,本文的算法在素布、花布的颜色校正上都得到很不错的效果,对最后1张织物图片的校正结果与标准光照下的结果有些偏差,可能是由于采样的时候相机的曝光度太高所致,其余3张织物的校正结果都与标准光照下的结果近似。

表4是不同织物颜色恒常性算法的色度误差统计结果。从表4可以看出,本文的算法虽然在最小值与平均值上不是最小的,但最大值与标准差是所有算法中最小的,说明算法具有良好的预测性能。同时,标准差最小也表明算法的稳定性比较好。

表4 不同织物颜色恒常性算法的色度误差统计结果Table 4 Chromaticity error statistics of different fabric color constancy algorithms

3 结 论

本文提出了一种基于改进ShuffleNetV2的织物颜色恒常性算法,解决了目前算法部署在计算机资源有限的移动终端的适配性不强、实时准确校正织物的色偏准确率不高的问题。在2个公共数据集结果表明,该算法在FLOPs、参数量较低的情况下,性能保持较高的水平。在NUS数据集上,角度误差的均值、最好25%、最差25%指标上有着最优的结果,在均值与中值指标上有着竞争性的结果。在Gehler-shi数据集上,角度误差的中值、均值、三均值指标上都有最优的结果,在最好25%、最差25%指标上有着竞争性的结果。最后,该算法用于织物的颜色校正取得了满意的效果,不足之处在于一些织物采集曝光度过高导致与矫正过的织物差别较大。下一步将会重点研究多光源下的颜色恒常性,提高算法的实用性。