变电站高耸避雷针风灾易损性分析*
2023-07-05张军锋贾继龙董新胜管品武
张军锋 贾继龙 董新胜 管品武
(1.郑州大学土木工程学院, 郑州 450001; 2.国网新疆电力公司电力科学研究院, 乌鲁木齐 830011)
0 引 言
变电站作为电网的关键节点,其安全性至关重要。为避免雷击现象,变电站内往往建立高耸的独立避雷针,或者是在变电构架上安装避雷针,以保护设备安全。作为典型的高耸结构,避雷针结构的风振效应较为显著,并且偶有风致倒塌事故[1]。结构易损性分析可从概率角度定量地预估结构的受灾情况,该方法首先在抗震分析中提出[2-3],并且逐渐应用到风致破坏分析中[4-5]。但相比丰富的地震易损性研究成果,风荷载作用下结构的易损性分析相对较少。因此,本文尝试对避雷针在风荷载作用下的安全性采用易损性分析方法[6-7]进行评价。
1 工程背景和风振计算方法
本工程位于新疆某750 kV变电站(图1),高度60 m,其中顶部塔尖2 m,下部58 m塔身由7段变截面薄壁钢管组成,采用Q345钢材,每段钢管之间采用插接+法兰盘连接,钢管尺寸和插接长度见图1。建模计算在ANSYS中进行,沿高度划分30个变截面Beam188单元,所得基频为0.751 Hz,详细工程介绍和建模计算可见文献[1]。

a—现场照片; b—尺寸示意。图1 避雷针几何参数 mFig.1 Geometric parameters of the lightning rod
根据GB 50009—2012《建筑结构荷载规范》[8]可知,结构处于B类场地,场地基本风速为V0=35.8 m/s。采用谐波合成法依Davenport谱进行脉动风场模拟,再由准定常气动力假定得各高度位置的脉动风荷载时程进行风振响应计算,计算时取阻尼比为1%,具体过程见文献[9]。图2给出了目标谱与模拟所得4个高度脉动风速样本风谱,可见模拟效果良好。另外,在静力风荷载Pushover分析和风振计算分析中采用BKIN双线性随动强化模型考虑钢材的非线性特征(图3)。
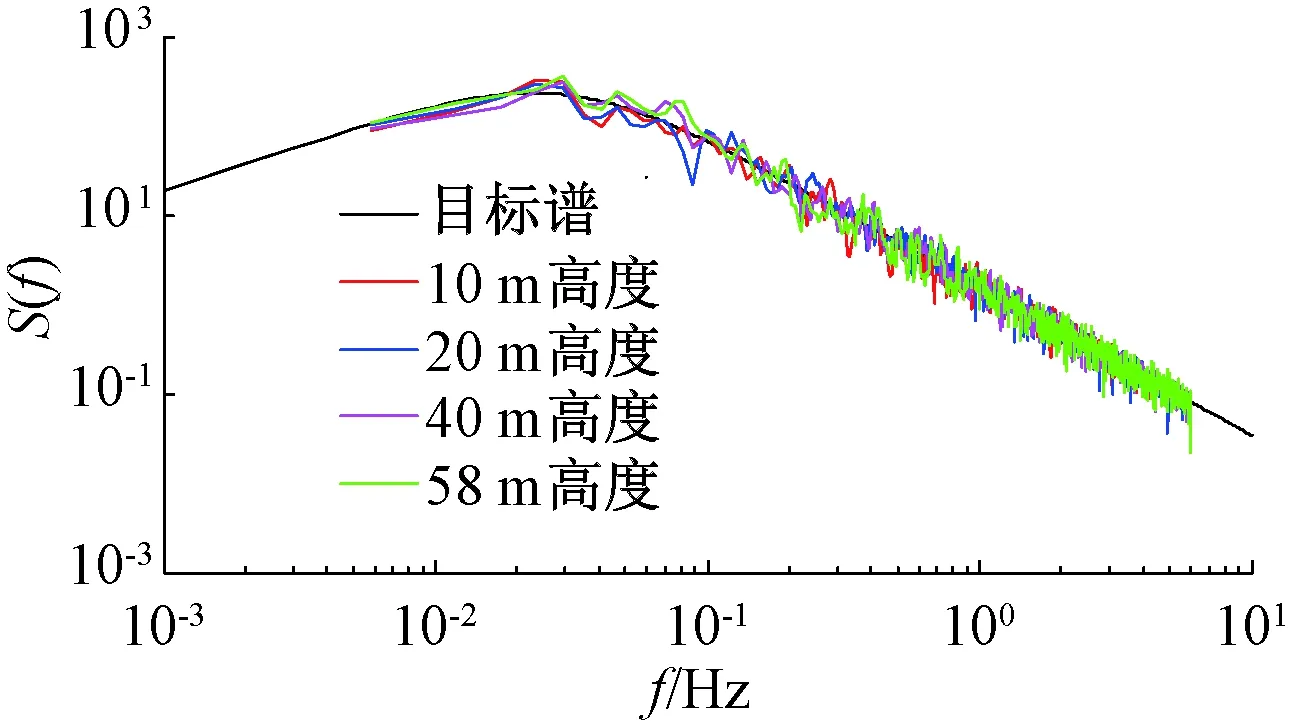
图2 V0=35.8 m/s时目标谱与模拟所得4个高度脉动风速样本风谱Fig.2 The target and simulated fluctuation wind speed spectrum forfour locations at V0=35.8 m/s
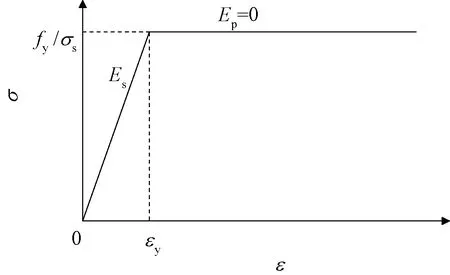
图3 钢材的非线性本构模型Fig.3 The nonlinear constitutive model of the steel
2 基于性能的风灾易损性分析
2.1 易损性分析理论
易损性是在一定荷载强度作用下,结构响应超过某种指定极限状态的条件失效概率(式(1))[10-14]:
Pf=P[R≥LS∣IM=x]=P[Sd≥Sc∣IM=x]
(1)
式中:Pf为结构的失效概率;R为荷载作用下的结构响应,对应结构需求D;LS为结构损伤极限状态,对应结构能力C;在确定了反映结构损伤的指标后,R和LS即为该指标的响应和性能水准量化值,两者可分别通过非线性动力分析和静力Pushover分析得到;IM=x是表征随机荷载强度大小的参数。上述概率分析方法不仅适用于地震易损性分析,也同样适用于风灾易损性分析[6,15],可分别对IM取用地面峰值加速度VPGA或基本风速V10。
考虑到结构和荷载的随机性并根据经典可靠度理论,一般假定R和LS都服从对数正态分布,则式(1)可以转化为式(2)。
(2)
其中k=Sd/Sc
式中:Ф为标准正态分布函数;Sd,Sc分别为需求与能力均值;βd,βc分别为需求与能力的对数标准差;k为需求能力比。这些参数的确定是易损性分析的关键,需要考虑结构和荷载的随机性进行分析。
2.2 结构和荷载随机样本生成
易损性分析实际上考察了结构的需求能力比,荷载和结构的不确定性均会影响易损性分析的结果[6,11]。研究中应同时考虑荷载和结构的不确定性,分析避雷针结构在不同风速下的结构响应,以及可能产生不同水准破坏的概率。根据结构特点,结合GB 50017—2017《钢结构设计标准》[16],以结构钢材的弹性模量、钢材的密度以及设计强度为不确定参数,假定以上参数均服从正态分布且取变异系数5%,采用拉丁超立方抽样法(LHS)进行抽样,得到3种随机参数的10组样本值(表1)。考虑风荷载的随机性,基本风速V0的调整范围为30~85 m/s,对每隔2 m/s一个样本进行脉动风时程模拟和风振计算。

表1 材料参数抽样Table 1 Material parameter sampling
2.3 损伤指标的确定及量化
基于性能的设计方法目前已被国内外众多学者认同,其目标是控制结构在不同强度荷载作用下的破坏程度,以达到预期的结构性能。这就需要首先选择能够合理反映结构能力C与需求D的损伤指标,以量化破坏极限状态[11]。针对建筑结构的抗震设计,确定目标位移是基于性能/位移设计的关键[17],在实际基于性能的地震易损性分析中,能力C与需求D往往都采用位移响应[7,13]或弯矩-曲率关系[14]为指标。在高耸结构的风灾易损性分析中,位移[13,18-20]和顶部位移角[6]也常作为控制指标对结构性能水平进行量化分析。对于风荷载作用下的高耸避雷针结构,其顶点位移u同样具有反映结构整体变形程度、真实反映结构损伤且便于使用的特点,因此选择结构顶点位移u划分性能水准,并将性能表现划分为基本完好、轻微破坏、中等破坏和严重破坏共四种状态。
具体过程如下[6,20]:通过各结构样本在GB 50009—2012静风荷载作用下的Pushover分析,确定结构出现屈服点时对应的顶点位移umo作为轻微破坏和中等破坏的界限,以1.3umo作为中等破坏和严重破坏的界限,以0.8umo作为基本完好和轻微破坏的界限,再通过对各样本界限值取均值来定义结构的性能水准[3,6-7](图4、表2)。
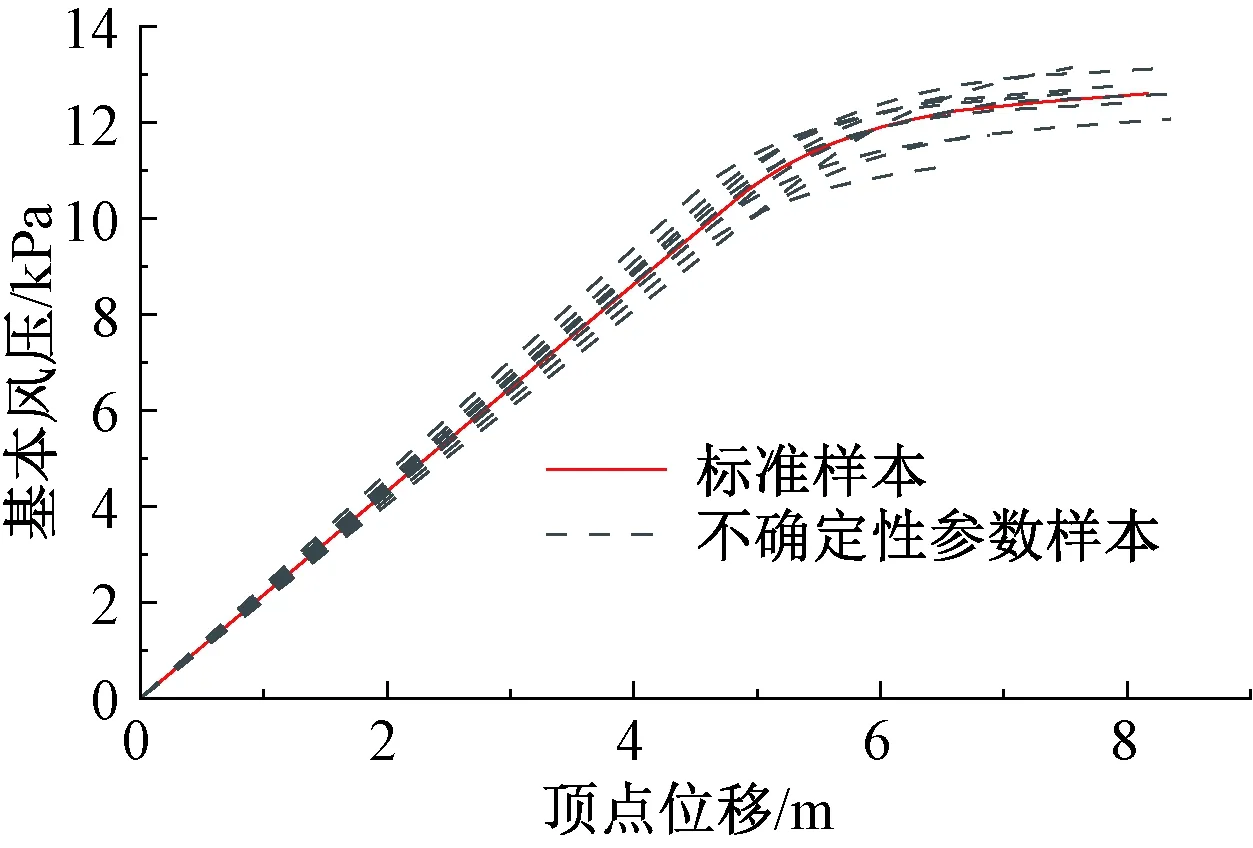
图4 避雷针顶端的荷载-位移曲线Fig.4 The load-displacement curves of the top of rods

表2 不同性能水平量化水准Table 2 Quantitative levels of differentperformance levels m
需要指出,由于各结构样本的随机性服从正态分布,文献[21-22]仅以结构标准样本进行Pushover分析得到界限值来定义性能水准。该方法与前述方法所得界限值较为接近,尤其是对于构件较少的简单结构:本算例采用两种方法得到的界限值偏差不足1%。
2.4 结构响应需求与荷载强度关系拟合
在易损性分析中,还需对大量随机结构和荷载样本动力作用下的结果进行拟合,以明确结构需求Sd与由基本风速V10所表达的荷载强度之间的关系。因Sc为定值,通过分析可采用式(3)进行拟合:
lnk=alnV10+b
(3)
式中:a、b为回归方程待定系数,可用最小二乘法确定,由此还可得回归分析标准差σ:
(4)

2.5 回归分析及易损性曲线
对各结构样本在不同风速下进行非线性动力时程分析并获得塔顶位移峰值,将所得结构需求与不同性能水准的位移限值(表2)根据式(2)计算得到需求能力比k,并对不同性能水准下的结构分别进行对数回归分析,如图5所示。可以看出,lnV10和lnk近似呈线性变化,这也验证了式(3)的合理性。同时也可看出,随着风速的逐渐增大,数据的离散性也愈加明显。这是因为结构在达到一定风速之后会进入屈服阶段,且结构屈服强度亦具有不确定性。
根据上述3种破坏模式(轻微、中等和严重破坏)的回归分析结果和式(2),绘制不同风速下的失效概率,得到避雷针结构风灾易损性曲线如图6所示。可以看出:在V10<60 m/s时,结构处于基本完好状态;当V10>60 m/s时,结构的响应随着风速的增大而增大,结构产生轻微破坏的概率逐渐增加;当V10达到70 m/s时,结构发生轻微破坏的概率接近1.0,并且逐渐开始发生中等破坏,此时结构也开始进入塑性阶段;在V10=80 m/s时,发生中等破坏的概率为0.98;V10=85~90 m/s时,结构发生轻微破坏和中等破坏的概率均到达1.0,此时结构发生严重破坏的概率也迅速增大,说明此时结构已临近倒塌。由此分析可知,在场址常规良态气候下,当风速V10<60 m/s时,结构的抗风安全性是可以保证的。
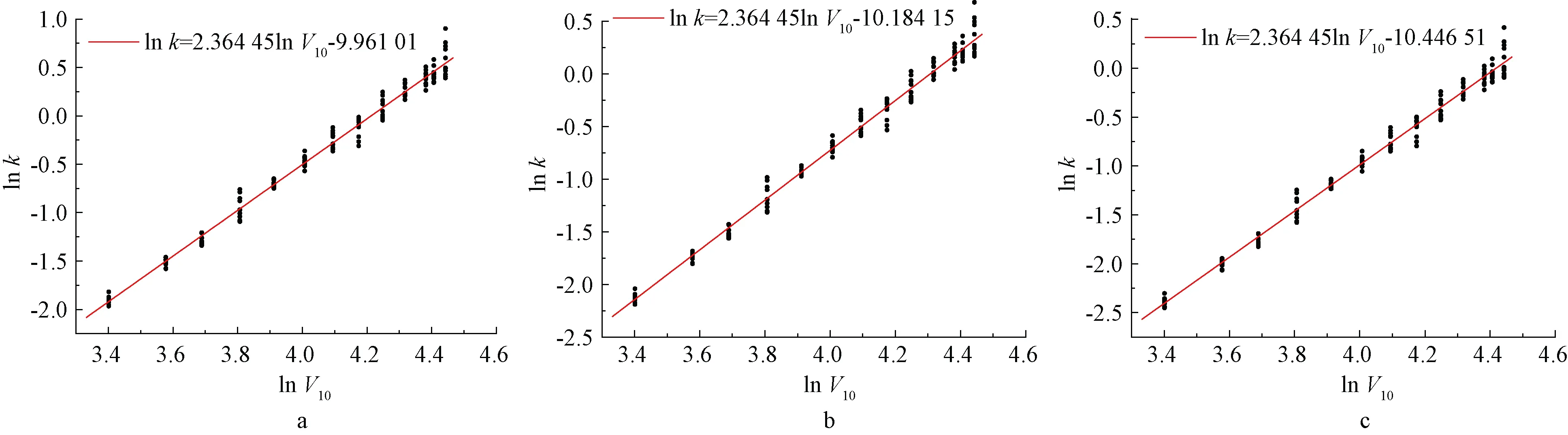
a—轻微破坏模式; b—中等破坏模式; c—严重破坏模式。图5 各性能水平下的回归分析Fig.5 Regression analysis at each performance level
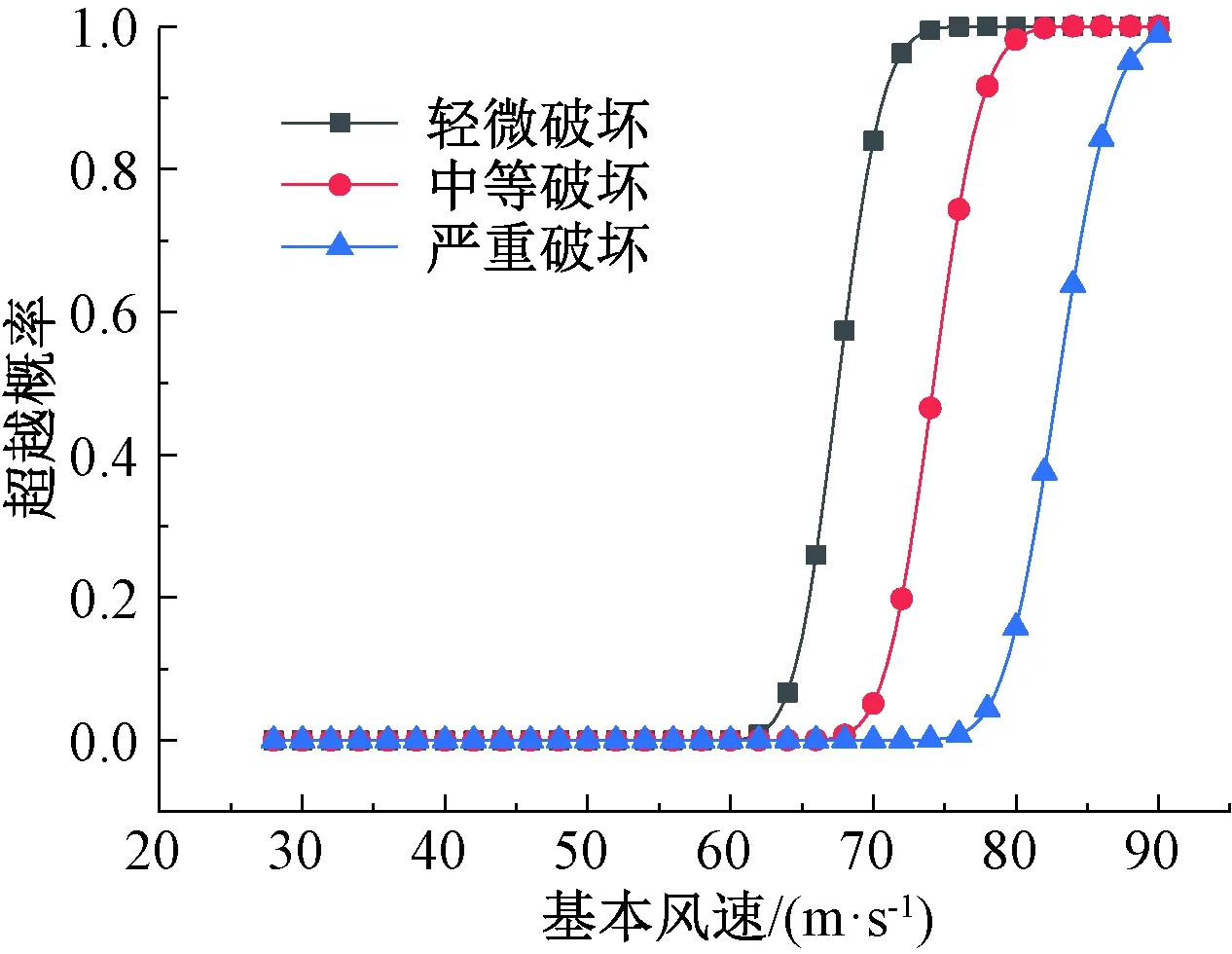
图6 避雷针风灾易损性曲线Fig.6 Wind disaster vulnerability curves of the lightning rod
2.6 回归分析方式的讨论
风灾易损性分析中,结构响应与荷载强度的回归分析多采用地震易损性分析中的双对数拟合方法(式(3)),但亦有文献采用式(5)进行拟合[6,23]。本节就此两种拟合方式进行讨论。
lnk=aV10+b
(5)
地震易损性分析中的双对数拟合方法源于文献[25]的假定,即地震需求参数的均值Sd与地震动强度参数IM呈指数关系(式(6a)),将其变换形式即可得式(3)。结构风工程分析中,在气动准定常假定下,风速与荷载成二次方关系,在结构线弹性分析中,响应与荷载成线性关系,即有式(6b)成立。
Sd=β(IM)a
(6a)
Sd=γ(V10)2
(6b)
式中:a、β和γ为待定参数。
由式(6)可知,两者形式接近,均可变换为式(3),并且对于式(6b),其变换成式(3)后对应的a=2.0。但是,在实际风振分析中,因风致动力效应和材料非线性的参与,结构响应与风速并不满足式(6b):本例回归所得系数a=2.364 5而非2.0。
图7和图8也给出了针对轻微破坏状态分别采用式(3)和式(5)所得拟合结果和易损性曲线。可以看出:式(5)所得拟合结果的偏差随着风速的增大而显著增加,且样本数据的截止风速对拟合斜率有较大影响,从而对易损性曲线也有较大影响,并且随着截止风速的增大,结构响应的塑性程度增大,但易损性曲线却不断后移,结构安全性反倒有所提高,这点与常识相悖。而式(3)拟合结果和易损性曲线受截止风速的影响可以忽略。由此可说明,在风灾易损性分析中应采用式(3)进行拟合。

a—ln k-V10拟合; b—ln k-ln V10拟合。图7 两种拟合方式所得结果Fig.7 Results obtained by two fitting methods
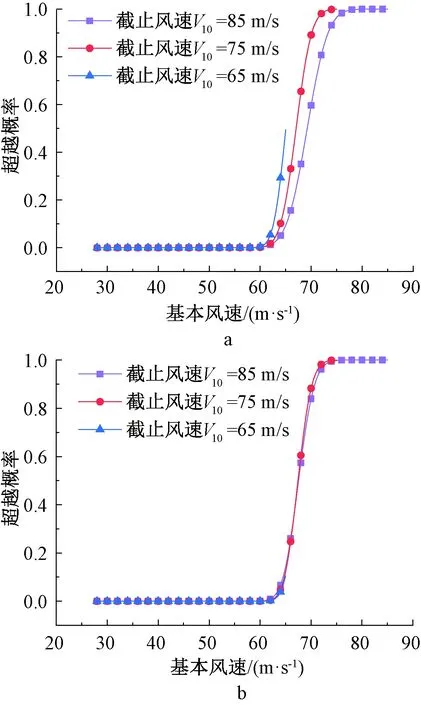
a—ln k-V10拟合; b—ln k-ln V10拟合。图8 两种拟合方式易损性曲线Fig.8 Vulnerability curves of two fitting methods
3 结束语
针对变电站高耸避雷针的风致倒塌事故,以一代表性工程为例展开风灾易损性分析。采用结构拉丁超立方抽样和脉动风场模拟以同时考虑结构和风荷载作用的随机性,通过考虑材料非线性的静力Pushover计算和增量动力时程计算获取结构静动力响应;在基于性能的分析框架下,确定结构顶端位移为损伤指标并给出了4种性能水准的量化值;通过对结构响应需求与荷载强度的回归分析和易损性函数获得易损性曲线。结果表明,在场址常规良态气候下,当基本风速V10<60 m/s时,结构的抗风安全性是可以保证的。另外,对结构响应需求与荷载强度的回归拟合方式也进行了讨论,在风灾易损性分析中,对结构响应需求和荷载强度的回归拟合方式采用双对数形式更为合理。
