基于无限元边界的输水隧洞爆破振动对周边高压输电铁塔的安全评估与优化*

赵 勇 豆红强 王 鹏 孙永鑫

(1.国网山东省电力公司, 济南 250001; 2.福州大学紫金地质与矿业学院, 福州 350108;3.国网山东省电力公司经济技术研究院, 济南 250000)

0 引 言

近年来,随着国内水利水电工程的蓬勃发展,作为水库工程中的一项最为关键和重要的工程组成部分,输水隧洞的建设方兴未艾。当前,输水隧洞的开挖施工仍以钻爆法为主[1-2],由爆破产生的振动将不可避免地对周边建(构)筑物的安全性产生不利影响。与此同时,高压输电铁塔是由杆件构成的空间桁架结构,其具有刚度小、对振动荷载敏感的特点。一旦输水隧洞邻近既有高压输电铁塔采用钻爆法施工时,其对铁塔塔基与塔身的爆破振动效应亟须重点关注。

事实上,国内外众多学者已对爆破开挖施工引起的爆破振动效应及其对临近建(构)筑物的爆破动力响应特征开展了大量研究。如田力等研究了地下隧道内的爆炸冲击对双层柱面网壳结构的动力响应特征[3];Xia等则依托大茂山新建隧道工程探讨了爆破开挖对既有隧道的动力响应规律,并提出了基于损伤控制的质点峰值振速的安全判据[4];邹玉君等依托白鹤滩水电站右岸坝肩以上边坡爆破开挖工程,基于监测数据对爆破振动的影响范围及程度进行分区,针对不同类型的房屋振动响应提出相应的振动控制措施[5]。但总体而言,当前对爆破开挖下的高压输电铁塔这一柔性空间结构的动力响应仍缺乏基本研究,且研究手段仍集中在现场实测分析或基于静力分析的数值模拟。如余顺等针对茶山隧道下穿500 kV的高压输电铁塔工程,通过定性分析爆破参数,提出了全隧道采用短距离三台阶分次爆破开挖方案[6];阳军生等则基于所建的高压输电铁塔与大断面隧道相互作用的三维静力数值模型对施工方案进行了总体优化[7]。

另一方面,随着有限元分析计算软件在爆破领域的逐渐普及[8],动力有限元法为解决爆破振动下结构的动力响应提供了一种有效途径。但在动力分析中,若采用固定边界将使爆破地震波在边界处发生反射和折射,并与岩土体中传播的波相互叠加,势必影响数值计算结果的准确性。为解决上述问题,学者们陆续提出诸如黏性边界[9]、透射边界、黏弹性边界[10]以及无限元边界[11]等。其中,无限元常常与常规有限元同时用来解决更复杂的无界问题,是对有限元方法的一种补充,因而,它与有限元方法的协调与生俱在,相较其他求解无界域问题的边界更具有优势[12-13]。

为此,以采用钻爆法施工的某输水隧洞临近高压输电铁塔为工程依托,建立爆破动荷载下基于无限元边界的动力数值模型,借此研究高压输电铁塔的动力响应特征。同时,以确保输电铁塔的正常运行并兼顾隧洞爆破开挖效率为目标,对爆破施工方案开展安全评估与优化工作。

1 工程概况

1.1 输水隧洞概况与周边高压输电铁塔的位置关系

拟建输水隧道为有压隧洞,隧洞进、出口为盲洞,其开挖断面采用城门型,洞径净截面尺寸为4.00 m×4.25 m(宽×高),洞身全长约712.66 m。沿线为低山丘陵地貌单元,山体雄厚,植被发育,地面高程为46～235 m(采用1985年国家高程基准),未见有滑坡、崩塌、泥石流等不良物理地质现象。隧洞洞身段沿线岩性基本为角砾凝灰熔岩,多呈强-弱风化,地质条件简单,未发现有大的断裂构造。第四纪覆盖层主要为残坡积土,分布厚度较小,约3～5 m。

在该输水隧洞300 m范围内通有3条500 kV输电线路,共有6个基塔。各塔均为500 kV正伞形直线塔,呼高范围在39～69 m,基础均为挖孔灌注桩基础,基底高程范围为92.3～194.8 m。基塔均位于该输水隧洞南侧,塔基底与隧洞高差均超过50 m,水平距离为49～224 m之间。各塔位与输水隧洞的相对位置如图1所示,塔位与隧洞近点相对距离如表1所列。

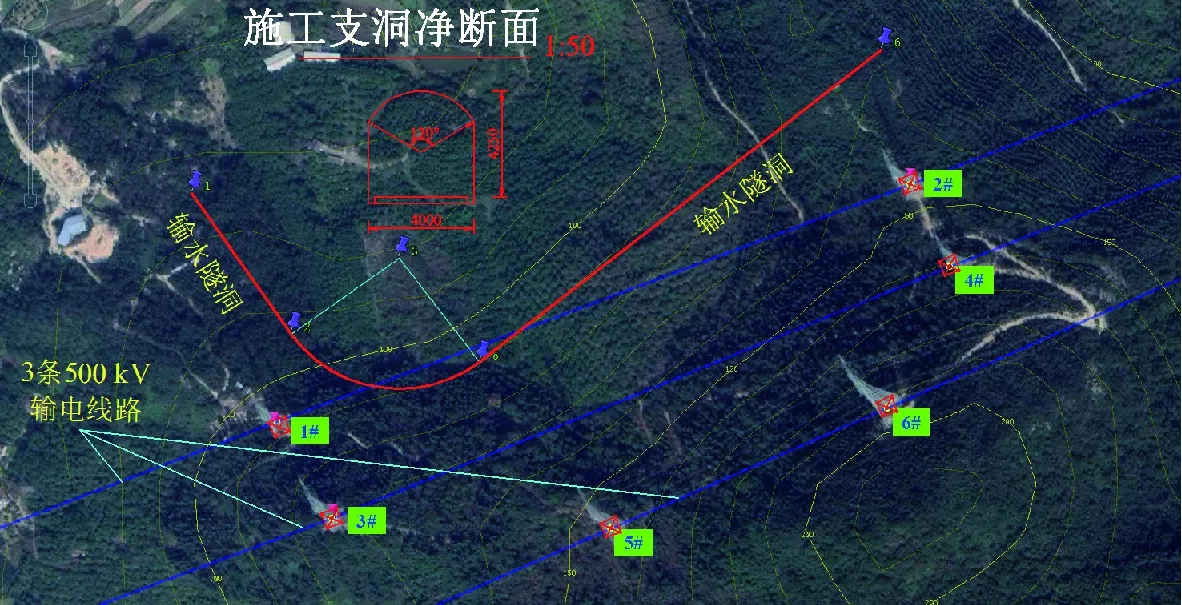
图1 塔位与输水隧洞相对位置平面Fig.1 Relative location plan of towers and the outlet tunnel

表1 塔位与输水隧洞近点距离

1.2 拟订的爆破施工方案

因该输水隧洞断面小,作业空间狭窄,拟采用钻爆法开挖施工,爆破方量约为11 392 m3。根据洞身围岩类别与输电基塔相对位置关系制定了3种施工方案。

1.2.1方案1

进洞段洞室上覆岩体厚度较薄,洞室围岩为强～弱风化,岩体破碎,围岩以Ⅳ类为主。采用全断面爆破开挖,每循环进尺0.8 m,楔形掏槽孔布置在断面中心偏下的位置,孔深为1.2 m,设计最大单次起爆药量为23.5 kg。图2a即为该方案相应的钻爆设计参数与布孔示意。

1.2.2方案2

该方案用于洞室以Ⅱ、Ⅲ类围岩为主的工况,采用全断面爆破开挖,每循环进尺1.8 m,采用复式楔形掏槽,掏槽孔孔深为2.2 m,设计最大单次起爆药量为53.8 kg。其钻爆设计参数与布孔示意如图2b所示。

1.2.3方案3

当输水隧洞下穿高压输电铁塔时,采用小进尺、多循环毫秒延期控制爆破技术,半断面爆破开挖,每循环进尺0.5 m,最大单次起爆药量为8.8 kg。图2c为其钻爆设计参数与布孔示意。

a—方案1; b—方案2; c—方案3。图2 拟订的三种爆破开挖施工方案 mmFig.2 Three proposed blasting excavation schemes

2 基于数值计算模型的安全评估方法

以距输水隧道最近的1号输电铁塔塔位为研究对象,其桩基础直径为0.6 m,桩长为11.2 m。同时依据该输水隧洞平面图、纵断面图、工程勘察报告以及1号塔位与输水隧洞的相对位置,可推断出其地质剖面图,进而可确定输水隧洞爆破开挖(爆破施工方案3)开展数值计算所需的几何模型,如图3所示。

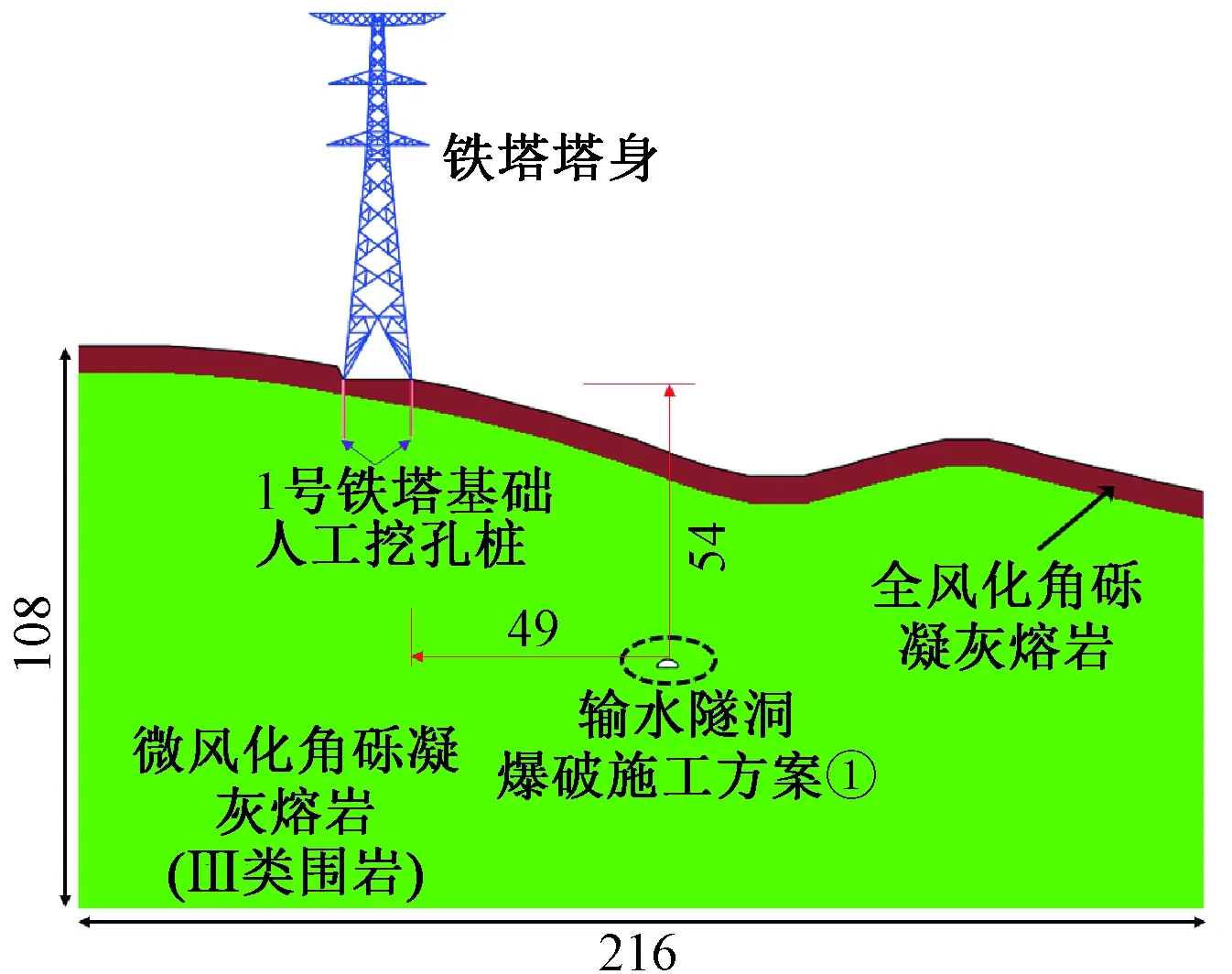
图3 数值计算的几何模型 mFig.3 Geometry of the numerical model

2.1 无限元边界的实现

在动力分析中,固定边界最大的问题就是导致波动在人工边界界面上反射,从而使能量传回分析区域而无法向无穷远传播。为此,基于ABAQUS平台引入无限单元边界,即通过在边界上引入分布阻尼力来吸收平面体波的辐射能量[11],由阻尼所产生的应力可表示为:

(1)

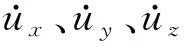
(2)

式中:cp和cs分别为纵波和横波的传播波速。

尽管ABAQUS提供了一阶和二阶无限元单元,但在ABAQUS的前处理中并不能对其予以直接定义。此时,可基于无限单元定义的理论与ABAQUS中单元和节点的定义规则,借助Python语言实现输出无限单元定义的数据行,重新对其节点进行编号,并令无限单元的第一个面为有限单元和无限单元的交界面,以保证无限元单元的延伸方向是从近区到远区。图4即为该输水隧洞爆破开挖对其临近输电铁塔动力响应数值模型的网格单元剖分,其在模型两侧与底部均采用了无限单元以吸收爆炸传递至边界的能量。

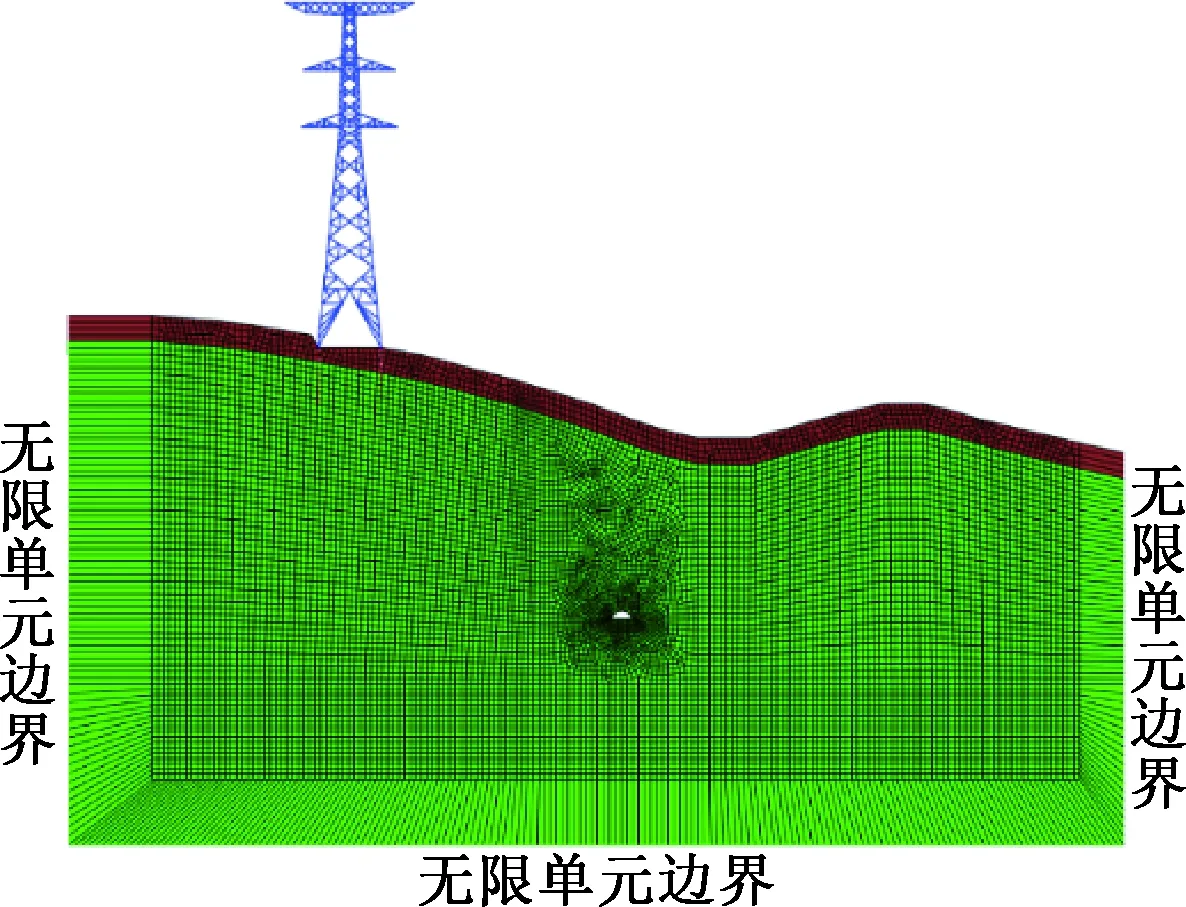
图4 网格划分Fig.4 Meshing of the numerical model

2.2 计算荷载的确定与施加

计算模型中的荷载包括岩土体自重荷载、铁塔自重、铁塔导地线等外荷载以及有爆破所产生的瞬时冲击荷载。其中岩土体自重荷载已形成初始应力场,其可借助Geostatic分析步根据岩土体重度参数自行生成。铁塔自重荷载与导地线等外荷载根据原设计荷载在静力分析步中予以等效施加。

对爆破荷载而言,本文拟采用美国National Highway Institute提及的公式,并认为一般耦合装药爆破的爆破压力均加载在孔壁的垂直方向上,则每千克炸药所产生的爆破荷载如下:

(3)

式中:Pb为孔内压力,MPa;Sge为火药比重;ve为爆破速度,m/s。

在不耦合装药的情况下,爆炸所产生的孔内压力小于耦合装药工况下的压力,两者之间的关系为:

(4)

式中:PbN为不耦合装药时的孔内压力;PbC为耦合装药时的孔内压力;dc为药卷直径,m;dh为炮眼直径,m;n为系数,对于柱状装药,n=2,对于集中装药和球状装药,n=3;υ为绝热系数,突变前取3,突变后取1.4。

岩体中传播的爆炸荷载在装药与岩体的界面上所给予的最大压力荷载与岩体特性有关,其与爆炸孔内压力的关系可近似表达为:

(5)

式中:ρr为岩体密度;vr为岩体的纵波传播速度;ρge为火药密度。

同时,为简化问题,假定所有爆破孔集中在一个位置,荷载压力同时作用在爆破的隧道壁上,作用方向为法向,此即为等效荷载法,相应的转化表达式为:

(6)

式中:a为爆破间距;Pemax为等效后施加在隧道壁上的荷载。

对于爆破荷载作用时间,一般认为炮孔爆轰压力变化历程中爆轰压力作用时间在10-6-10-1s范围,参考前人的处理方法,采用三角型荷载进行爆破作用的模拟[14],从初始无压状态加载到压力峰值的升压时间取为100 μs,正压力作用时间取为600 μs,采用动力隐式分析步在输水隧道上断面洞壁上施加上述爆炸荷载,同时为了模拟爆炸荷载的传递过程,取计算时长为0.6 s。

2.3 模型计算参数

模型中计算参数的选取可依据勘察报告所给的建议值。其中,全风化角砾凝灰熔岩与微风化角砾凝灰熔岩采用Mohr-Coulomb弹塑性模型,并采用CPE4R实体单元予以模拟;输电铁塔基础人工挖孔桩(直径为0.6 m)则采用线弹性模型,并用梁单元模拟其力学性能。同时,铁塔作为柔性空间结构,其构造和受力比较复杂,为简化处理,可将铁塔简化成梁桁混合模型,即:1)将铁塔的4根主材简化成梁单元,截面型式尺寸与实际完全相同,其他斜材、辅材等全部简化成桁架单元;2)假设桁架的节点都是光滑的铰链连接,各杆件的轴线均为直线并通过铰心;3)梁单元与桁架单元假定为理想连接;4)外力都作用在节点上。相应的计算参数如表2所示。

表2 数值模型计算参数Table 2 Calculating parameters for the numerical model

3 数值计算结果分析

3.1 两种边界条件的对比

为验证无限元边界的合理性,现选取输电铁塔基础的桩顶与桩端为特征点,提取其振速时程曲线,并与固定边界的计算结果进行对比,如图5所示。可以看出,当爆破荷载传递至桩顶和桩端处时,基于无限元边界所得的振速陡然增加,此后迅速衰减并趋于零;而基于固定边界所得的振速则表现为波动式的衰减,这是由于爆破所产生的能量无法透过固定边界向远域辐射,在计算区域内引起反复振荡,表明固定边界对内源振动输入的影响较大,而无限元边界则能较好地吸收散射波。因此,基于无限元边界的计算结果相对可靠且具有一定的稳定性。

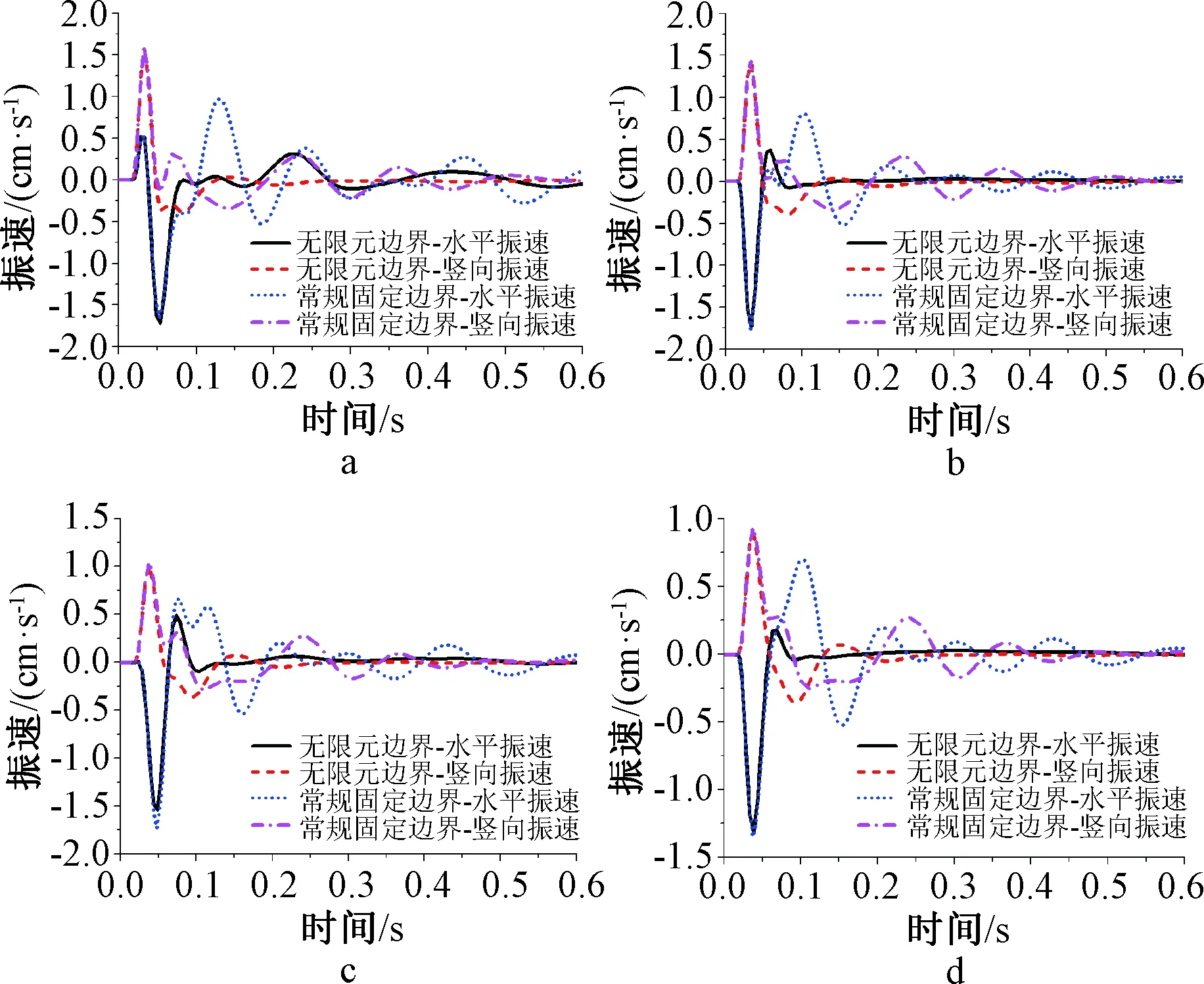
a—右桩桩顶; b—右桩桩端; c—左桩桩顶; d—左桩桩端。图5 振速时程曲线Fig.5 Time-history curves of vibration velocity

3.2 塔基振动的安全评估

GB 6722—2014《爆破安全规程》[15]给出了一般建筑物的爆破振动安全允许质点振动速度,但未明确输电铁塔塔基的安全允许质点振动速度。对于一般民用建筑物,给出的安全允许质点振动速度约为2.5 cm/s,由此可以推断对于高压输电铁塔塔基,其安全允许质点振动速度应不大于2.5 cm/s。文中,为确保爆破冲击波不会严重影响输电线路的正常运行,制定的爆破技术方案选择了2.0 cm/s的峰值振动速度作为输电铁塔塔基的安全判定标准。

由图5可知,当采用爆破施工方案3时,右桩桩顶的最大水平振速约为1.72 cm/s,最大竖向振速约为1.57 cm/s;右桩桩端的最大水平振速约为1.73 cm/s,最大竖向振速约为1.40 cm/s。左桩桩顶的最大水平振速约为1.53 cm/s,最大竖向振速约为1.0 cm/s;左桩桩端的最大水平振速约为1.31 cm/s,最大竖向振速约为0.88 cm/s。同时对比可知,右侧桩达到最大振速的时间稍早于左侧桩,这恰恰反映了爆炸冲击荷载在围岩中的传递过程。综上,输电铁塔塔基的最大振速均小于2.0 cm/s,表明该施工方案可满足GB 6722—2014中关于最大允许振速的规定。

3.3 塔身振动规律与其安全评估

塔身作为一个复杂的柔性结构,在瞬时荷载作用下其最大振速所在位置时刻发生变化。为直观描述铁塔塔身在爆破冲击荷载作用下的振速分布情况,图6给出了不同时刻塔身合振速(水平向振速与竖直向振速的合成)的矢量分布图。

a—t=1.5×10-2 s; b—t=4.8×10-2 s;c—t=6.3×10-2 s; d—t=6.0×10-1 s。图6 不同时刻塔身合振速矢量 m/sFig.6 Resultant vibration velocity of the tower at different times

由图6可知:在t=1.5×10-2s之前,爆破冲击荷载尚未传至塔身,此时其振动速度接近于0;随着时间的推进,由爆破冲击荷载传递所引起的振速率先发生于塔身左侧底部;当t=4.8×10-2s时,爆破冲击荷载已传递至塔身右侧,此时最大振动速度发生于塔身右侧底部,其值约为1.684 cm/s;此后,爆破冲击荷载开始向塔身上部传递,同时由于塔身的放大效应,致使最大振速发生于塔身上部,其值约为1.918 cm/s(t=6.3×10-2s);此后,由于爆破所产生的冲击荷载逐渐衰减,塔身的最大振速也逐渐降低,当t=6.0×10-1s时,其最大振速仅为0.4 cm/s。

可见,在爆破冲击荷载作用下,塔身的最大合振速小于2.0 cm/s,亦表明其水平向最大振速和竖直向最大振速同样小于2.0 cm/s,进一步说明原拟订的输水隧洞下穿输电铁塔的爆破施工方案安全可行。

3.4 不同爆心距下的振速响应

由前所述,该数值模型在考虑爆破作用时是将等效计算的爆破荷载压力作用在隧洞壁上,即为该支洞剖面的上断面位置,类似于点源荷载。同时,由勘察报告可知,该输水隧洞围岩较为均一,则由爆破荷载所引起的围岩振动速度分布大致呈圆形向外扩展。此时,即可以爆破中心为基点,向外任意选取不同距离的点并提取其合振速时程曲线。从其振速时程曲线中选取最大振速,绘制如图7所示的振速-距离曲线。

图7 振速与距离的关系Fig.7 Relations between vibration velocity and distance

4 3种爆破施工方案的分区优化

前述已对下穿输电铁塔爆破施工方案3开展了安全评估,表明以2.0 cm/s的振动速度为控制条件时,施工方案3的安全距离临界值约为60.0 m。但该输水隧洞掘进断面至输电铁塔距离为多大时,可由全面段爆破转换为半断面爆破仍未得到解答,亦即3种爆破施工方案所允许的适用范围还未明确。为此,采用上述同样的无限元边界数值模型来模拟不同爆破施工方案下振动速度的衰减规律。

图8即给出了3种不同爆破施工方案下距爆破中心不同距离特征点的最大合振速分布曲线。可知:在不同的爆破施工方案下,不同位置的最大合振速均随距爆破中心点距离的增加而近似呈指数函数形式的衰减;若以最大振动速度2.0 cm/s为控制条件,当采用施工方案1时,其对应安全距离约为88 m;当采用施工方案2时,其对应安全距离则为116 m。

图8 不同爆破施工方案下振速与距离的关系Fig.8 Relations between vibration velocity anddistance in different schemes

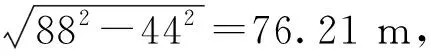
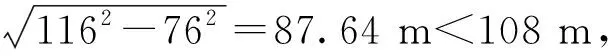
综上,结合场地勘察报告,该输水隧洞洞口0+000～0+043 m段洞室围岩为强～弱风化,岩体破碎,围岩以Ⅳ类为主,则可选择爆破施工方案1;在0+043～0+080 m段洞室围岩多为弱风化,岩体多呈破碎～完整性差,围岩以Ⅲ类为主,则可选择爆破施工方案2;在0+115～+215 m段,为确保1号输电铁塔的安全,该段务必采用施工方案3;在0+080～0+115 m段和0+215～0+247 m段,可采用施工方案1。此外,在0+247-0+663 m段,均可采用施工方案2。具体如图9所示。

图9 爆破方案优化平面Fig.9 Optimized plan of blasting scheme

5 结 论

本文根据拟建输水隧洞与既有高压输电铁塔的空间位置关系及其结构特征,建立了爆破动荷载下基于无限元边界的动力数值模型,采用质点振速作为该输电铁塔的安全评判准则,借此对拟采用的爆破施工方案进行了安全评估与优化分区,并得到以下结论:

1)基于常规固定边界计算所得的桩顶与桩端特征点的振速在计算域内表现为往复震荡式的衰减,而基于无限元边界所得的振速则表现快速衰减至零,表明无限边界可较好地反映爆破能量向半无限介质传播的真实情况,其所得结果相对可靠且具有一定的稳定性。

2)采用爆破施工方案3时,距输水隧洞洞身最近的1号高压输电铁塔的塔基与塔身的最大振速均小于2.0 cm/s,满足GB 6722—2014中的安全控制标准。

3)爆破荷载作用下围岩合振速随距爆破中心点距离大致呈指数级衰减,基于峰值振动速度(2.0 cm/s)的安全判定标准分别确定了3种爆破施工方案的临界安全距离,分别为60,88,116 m。并进一步根据输水隧洞围岩工程特性与高压输电铁塔的相对位置,明确并优化了三种爆破施工方案在该输水隧洞中的分区施工范围。