大跨越输电塔双平臂抱杆的风洞试验研究*
2023-07-05夏顺俊张仁强戴如章李锡民
夏顺俊 赵 俊 马 龙 张仁强 戴如章 李锡民
(江苏省送变电有限公司, 南京 210028)
0 引 言
我国东南沿海经济发达地区是电力需求最旺盛的区域,但当地电力资源往往不足,因此国家大力推进开展“西电东送”“北电南送”等长距离电力输送工程。这些新建的高电压、大容量、长距离的大跨越电力通道,面临着我国高山、大江和海峡等复杂地形地貌的阻隔和挑战,具有电压等级高、档距大和铁塔高等特征,属于技术难度高的超级电网工程。大跨越输电工程高塔施工过程中所采用的特殊吊装设备——抱杆,是组立输电高塔的关键起重机械,具有很好的适用性,已成功应用于舟山西堠门大跨越380 m高输电铁塔等超级输电工程[1-4]。
针对此类抱杆结构,已经开展了相应的现场试验和有限元分析研究工作。周焕林等采用有限元软件建立了舟山大跨越抱杆静力分析模型,并开展了现场试验以分析腰环、塔身等各构件的最大应力[5]。徐城城等建立了双平臂抱杆非线性有限元模型,分析得到了稳定性不利工况[6]。吴凡等针对抱杆与铁塔的耦合模型进行力学性能分析,发现耦合结构抱杆最大位移增大,腰环拉线拉力减小[7]。叶何凯对不同施工阶段的舟山大跨越抱杆及其与钢管塔的耦合体系进行风振响应时程分析,得到了风振系数和等效静力风荷载[8]。
抱杆结构在设计研制时,其风荷载计算可以参考GB 50009—2012《建筑结构荷载规范》[9](简称《规范》)、GB 50135—2019《高耸结构设计标准》[10](简称《标准》)及DL/T 5154—2012《架空送电线路杆塔结构设计技术规定》[11]等。但由于现行规范中不存在与抱杆各组成部件完全一一对应的风荷载取值规定,在实际设计中对抱杆构件体型系数的取值处理较为简化[12]。另外,规范中也没有严格考虑不同部件之间风效应的干扰特性,根据相关规范所确定的抱杆风荷载很可能与实际抱杆所受风力不符。本文通过风洞试验深入研究了抱杆结构的气动力特性和风效应干扰特性,为抱杆结构抗风设计及安全施工提供重要依据。
目前在建的凤城—梅里500 kV线路长江大跨越工程跨越塔高385 m,建成后将再一次刷新输电塔高的世界纪录。应用于该工程的双平臂抱杆在起重重量、作业幅度、起吊高度等指标上也均为世界同类型装备之最。针对该工程的双平臂抱杆开展了多姿态下的风洞试验,获取抱杆标准节、上部结构及整体结构的整体体型系数;同时采用构件总计法,计算得到了抱杆标准节的立体风力干涉系数,为实现抱杆体型系数的快速精细化计算提供参考。
1 工程概况
凤城—梅里500 kV线路长江大跨越工程的江阴长江大跨越工程基本为南北走向,如图1a所示,北岸跨越点位于靖江市新桥镇财神圩附近,南岸跨越点位于江阴市利港镇黄丹村同兴圩附近,两岸跨越塔及锚塔均位于堤内农田中,地形平坦开阔。大跨越耐张段全长4 055 m,跨越档距2 550 m。

a— 江阴长江大跨越位置; b—铁塔与抱杆 (2021年7月)。图1 江阴长江大跨越输电工程Fig.1 Long-span transmission project crossing theYangtze Rivers in Jiangyin
T2T1500双平臂抱杆结构如图1b所示,是为组立江阴长江大跨越385 m高塔设计制作的专业起重机械。该抱杆结构主要由标准节、过渡段、下支座、上支座、回转塔身、塔顶、平臂、平臂拉杆等部件组成,结构形式复杂。图2a~e给出了抱杆整体结构及其各组成部分及其尺寸。抱杆标准节立柱为HW400×400型钢,立柱主材截面及腹杆尺寸如图2f所示。
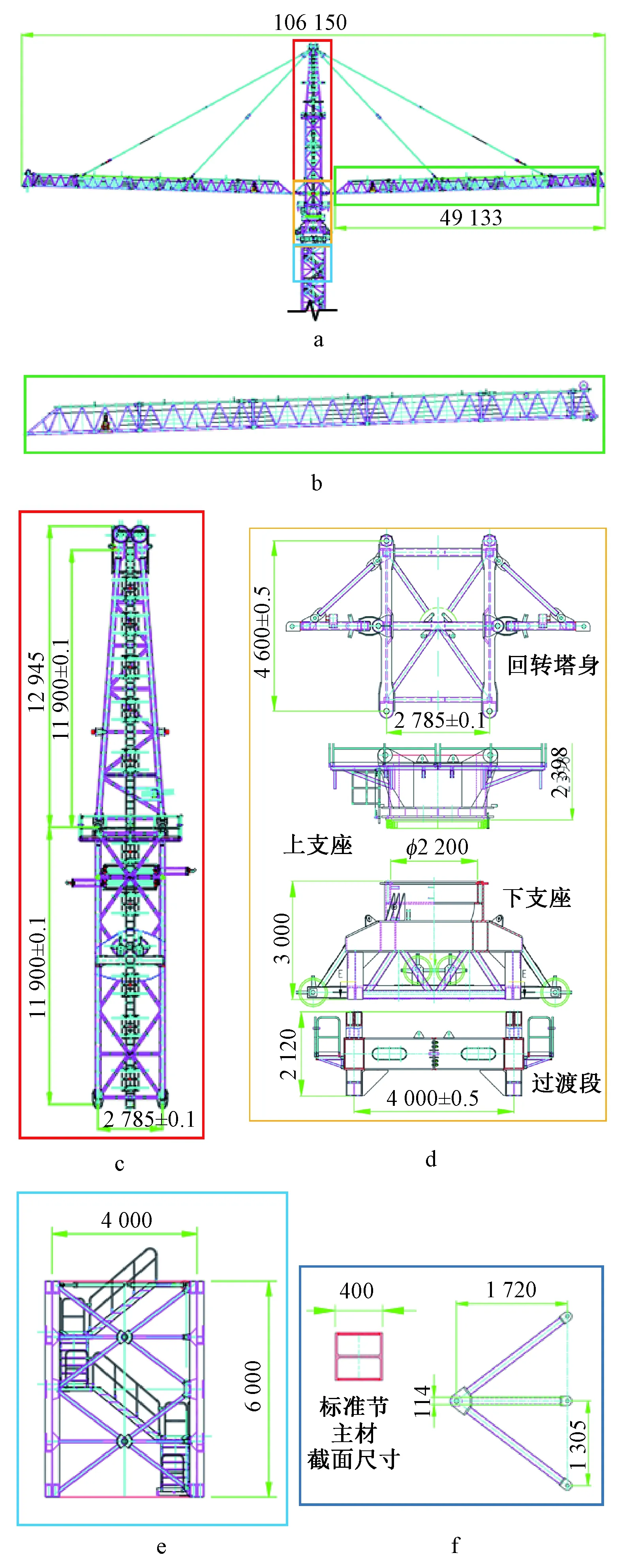
a—抱杆整体; b—平臂结构; c—塔顶结构; d—中段回转结构;e—单节标准节; f—标准节构件截面尺寸图2 抱杆整体及各组分结构 mmFig.2 Overall and component structures of the crane
2 风洞试验
2.1 试验设备
抱杆风洞试验在浙江大学的ZD-1边界层风洞中进行。ZD-1边界层风洞是一座单回流闭口立式边界层风洞。风洞集速压控制系统、转盘系统、三维移测架系统和安全监控系统于一体。风洞试验段尺寸为4 m(宽)×3 m(高)×18 m(长),空风洞试验段风速范围为3~55 m/s,控制精度达到1.0%以上。
试验中使用了高频底座测力天平,用于测量风洞模型所承受的总风力,包括6个分量(Fx、Fy、Fz、Mx、My和Mz),最大量程Fx=Fy=20 N,Fz=40 N,Mx=My=Mz=4 N·m,全量程测量精度为0.3%,采样频率最高可达1 kHz。
依据GB 50009—2012[9]中的规定,T2T1500双平臂抱杆所在的地区为A类地貌,地面粗糙度系数为0.12,大气边界层梯度高度为300 m。
T2T1500双平臂抱杆主要由标准节、过渡段、下支座、上支座、回转塔身、塔顶、平臂、平臂拉杆等组成,可以通过调整标准节的数目来调整抱杆整体的高度。考虑到最不利工作状态下,抱杆整体处于离地超过300 m的高空,位于大气边界层之上,此时风速不随高度发生变化。故本次风洞试验选用均匀流场作为试验风场。相较于高湍流度风速,格构式圆钢塔在低湍流度下测得的高频天平基底反力均值会略微偏大[13],因此在均匀流实验条件下最终计算得到的体型系数也偏向保守。
2.2 抱杆测力模型
T2T1500双平臂抱杆风洞试验模型按几何相似要求,采用ABS工程塑料制作而成。风洞试验模型共有两种,第一种为抱杆标准节节段模型,缩尺比为1∶20,风洞试验模型外观及布置如图3所示;第二种为含有16节标准节的抱杆整体模型,缩尺比为1∶100,如图4所示。两种模型在风洞中阻塞比均小于5%,满足风洞试验要求,因此试验所得的无量纲风力系数可直接应用于原型结构的抗风设计。

图3 抱杆标准节模型Fig.3 Standard segment model of the crane

图4 抱杆整体模型Fig.4 Overall model of the crane
2.3 抱杆标准节整体体型系数
抱杆标准节风荷载体型系数可计算如下[8]:
(1a)
(1b)
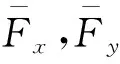
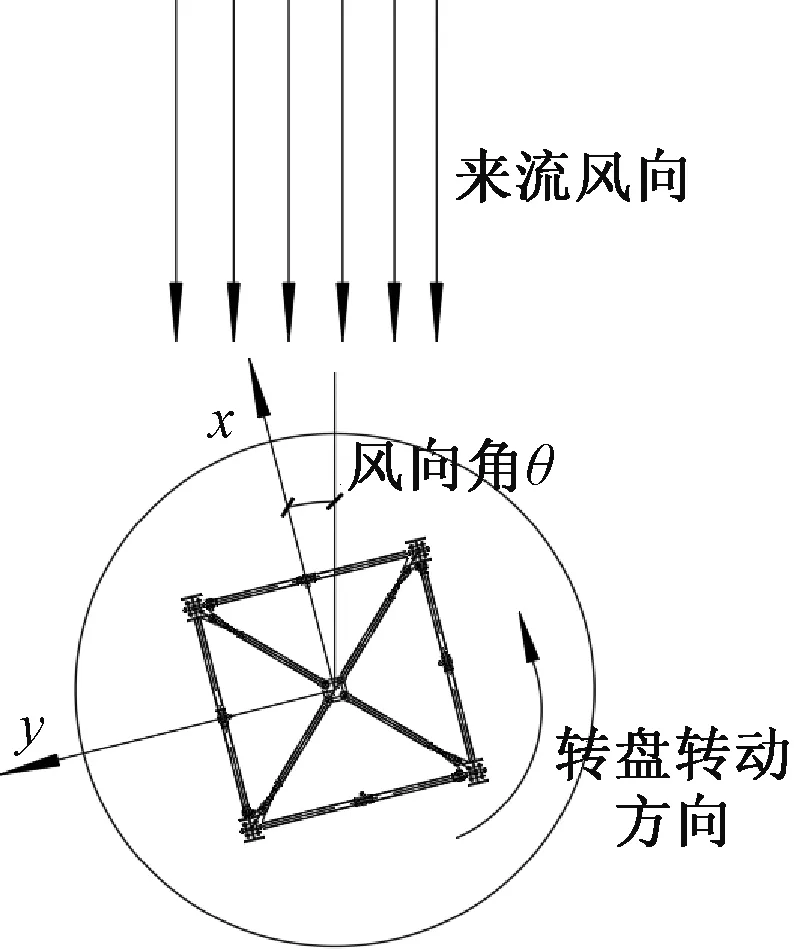
图5 抱杆标准节风力分量坐标系Fig.5 Wind component coordinate system of standard segment
根据x向和y向体型系数可得到抱杆标准节沿来流风向的整体体型系数:
(2)
式中:μs为来流风向抱杆标准节整体体型系数;θ为来流风向与抱杆标准节x向之间的夹角。
由于抱杆标准节x向与y向迎风面净投影面积相等,故式(2)可以简化为:
μs=μsxcosθ+μsysinθ
(3)
2.4 抱杆整体风力系数
T2T1500双平臂抱杆结构形式复杂,主要由塔顶、回转塔身、上支座、下支座、平臂、平臂拉杆、过渡段和多个标准节等组成。抱杆整体风力系数可定义如下:
(4a)
(4b)
式中:Cx,Cy分别为抱杆整体x向和y向风力系数,坐标系如图6所示;S为抱杆平臂位于0°时抱杆x向迎风面净投影总面积;Fx,Fy分别为抱杆沿x向和y向所承受的风力分量。
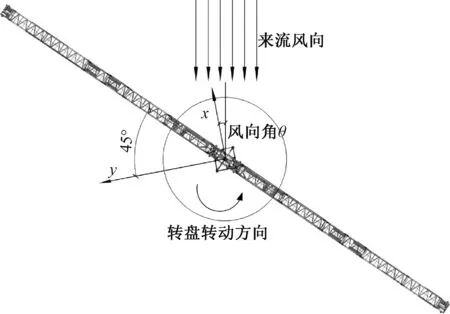
图6 抱杆整体模型姿态及试验风向角(以平臂在45°位置为例)Fig.6 Attitude of the overall crane model and incomingwind angles (with flat arm at 45° for example)
3 试验结果及分析
3.1 节段模型
3.1.1试验布置与测试工况
抱杆标准节节段模型缩尺比为1∶20,模型高0.9 m,共包含3段标准节,外侧宽度为0.22 m。为减少边界层效应可能对气动力测试产生的影响,将试验模型抬高以使其与风洞底面保持一段距离;为尽可能消除三维流效应,试验时在模型上下端布置端板来确保模型四周流场的二维特性,如图7所示。
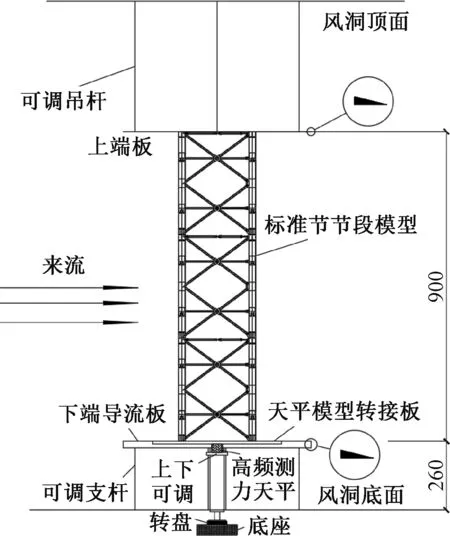
图7 节段模型试验布置 mmFig.7 Experiment set-up of segment model
参考《规范》[9]规定,空气密度取1.25 kg/m3。试验参考点设置在0.7 m高度处,测试风速为10 m/s,流场设置为均匀流。采用高频底座测力天平以500 Hz的采样频率测量模型底部6个分力。
基于平臂与标准节的相对位置关系,试验按逆时针设置0°、15°、22.5°、30°、37.5°、45°、52.5°、60°、67.5°、75°、82.5°、90°、97.5°、105°、112.5°、120°、135°共17个风向角的试验工况,试验风向角规定如图5所示。每个风向角高频天平采样时间为180 s。
3.1.2试验结果
试验所得抱杆标准节整体体型系数随风向角变化关系如图8所示。由于标准节模型各迎风面杆件布置中心对称,因此随着风向角的增大,抱杆标准节整体体型系数呈现出周期性变化态势。

图8 抱杆标准节整体体型系数随风向角变化关系Fig.8 Relations between the overall shape coefficients ofstandard segment and incoming wind angle
风洞试验所得抱杆标准节整体体型系数与《标准》[10]中塔架整体体型系数进行了对比,参见表1。
结果表明,按《标准》选取的抱杆整体体型系数在0°、45°和90°风向角时与风洞试验结果符合很好,误差很小。从图8中可以看出,抱杆标准节整体体型系数最大值出现在37.5°风向角位置,其值为2.78;在风向角为90°时则最小,为2.24;在风向角相对误差=(标准-风洞)/风洞。
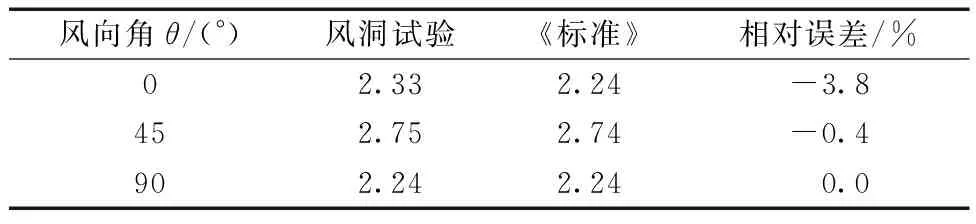
表1 抱杆标准节整体体型系数试验与《标准》的对比Table 1 Comparisons of overall shape coefficients ofstandard segments obtained from test and code
为52.5°时与37.5°时较为接近,为2.77,均略大于45°风向角下的2.74。在0°~45°、45°~90°和90°~135°风向角的范围内,抱杆标准节整体体型系数与风向角θ近似存在着线性变化的规律,对各分段进行线性拟合得到式(5),拟合线段如图8所示。实际工程中可基于式(5)计算抱杆标准节在任意风向角下的整体体型系数。
(5)
3.2 抱杆整体模型
3.2.1试验布置与测试工况
抱杆整体模型包含塔头、双平臂和16节标准节,缩尺比1∶100,模型高1.325 m,最大宽度为1.062 m。上支座以上部位(包括上支座、回转塔身、塔顶、平臂拉杆、平臂)设计成可相对标准节旋转3个角度,即0°、22.5°和45°,抱杆姿态及试验风向角如图6所示。由于整体模型较柔,为减小试验风振影响,测试风速设为6 m/s。考虑3种典型的抱杆相对于标准节的旋转角度,试验共设置21个试验工况,如表2所示。

表2 抱杆整体模型试验工况Table 2 Test conditions of the overall model of the crane
3.2.2试验结果
为了便于试验与《标准》之间进行对比,选用《标准》[10]中风向角的定义,如图9所示。根据文献[12],计算抱杆整体风力系数时,标准节、过渡段、回转塔身以及塔顶部分参考了塔架的体型系数[10],上下支座部分参考了绝缘子的体型系数[10],平臂部分参考了格构式横梁的体型系数[10];平臂拉杆参考了架空线的体型系数。

a—平臂在0°位置; b—平臂在22.5°位置; c—平臂在45°位置。图9 规范验算用风向角的定义Fig.9 Definition of wind angles for code verification
风洞试验得到的平臂在0°、22.5°、45°位置时抱杆整体x向和y向的风力系数随《标准》风向角的变化规律如图10和图11所示。试验与《标准》所得风力系数之间的对比见表3和表4。

图10 各平臂姿态抱杆x向整体风力系数Fig.10 Overall wind coefficients of the crane inx-direction for each flat arm attitude

图11 各平臂姿态抱杆y向整体风力系数Fig.11 Overall wind coefficients of the crane iny-direction for each flat arm attitude
由图10、图11可以得到:对于不同平臂姿态的抱杆整体x向风力系数结果,其值均随《标准》风向角的增加呈现逐渐增大的趋势,其中平臂在0°位置时,x向风力系数在《标准》风向角75°时达到最大值2.48;平臂在22.5°和45°位置时,x向风力系数在《标准》风向角90°时达到最大值,其值分别为2.40和1.69。观察抱杆整体y向风力系数结果可以发现,平臂在0°位置时,其值呈现先增大后减小的变化规律,并在《标准》风向角30°时取得最大值1.99;平臂在22.5°位置时,y向风力系数随《标准》风向角的增加先缓慢上升后快速下降,在《标准》风向角45°时取得最大值2.51;平臂在45°位置时,y向风力系数《标准》范风向角的增加波动上升,在《标准》风向角60°时达到最大值2.56,之后缓慢下降,并在《标准》风向角90°时接近x向风力系数。
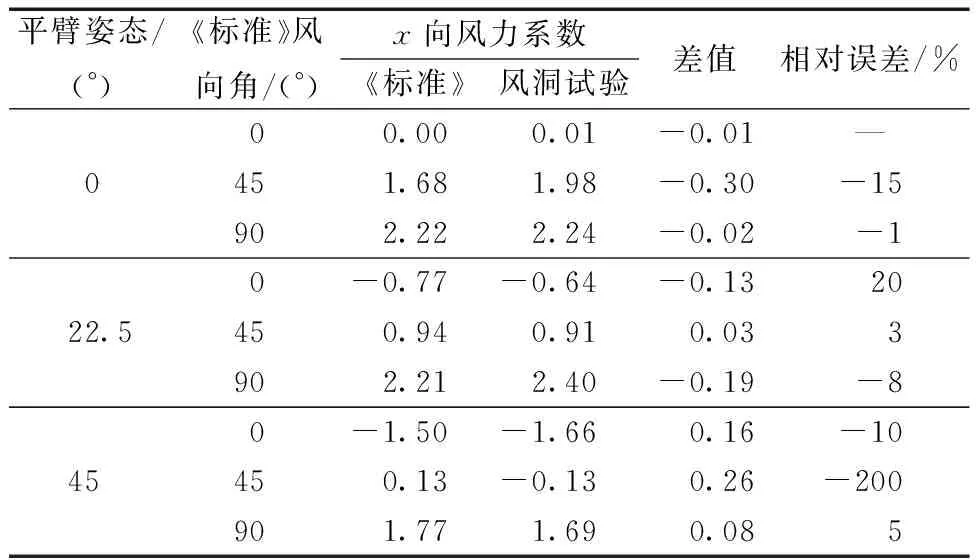
表3 抱杆整体模型x向风力系数与《标准》取值对比Table 3 Comparisons of the x-direction wind coefficientsof overall crane model with the code values

表4 抱杆整体模型y向风力系数与《标准》取值对比Table 4 Comparisons of the y-direction wind coefficientsof overall crane model with the code values
如表3和表4所示,x向风力系数《标准》取值与试验值之间的最大差值出现在0°平臂位置、《标准》风向角为45°时,《标准》取值与试验结果相差-0.3(表3);y向风力系数《标准》取值与试验值最大差值出现在22.5°平臂位置、《标准》风向角为45°时,《标准》取值比风洞试验结果小0.58(表4),严重低估了y向风力。考虑相对误差,在45°平臂位置、《标准》风向角为45°时,由于此时x向风力系数的风洞试验结果为负,因此其相对误差达200%,然而差值绝对值并非特别显著,其值为0.26;y向风力系数的《标准》取值与试验值相对误差最大则出现在0°平臂位置、《标准》风向角为0°时,《标准》取值比试验结果大33%。
抱杆整体风力系数的风洞试验结果与《标准》取值存在一定差异,且在某些风向角下《标准》取值严重低估了抱杆风力,故抱杆抗风结构的抗风验算应采用风洞试验结果。这种差异的主要原因是《标准》取值没有考虑到干扰效应。对于抱杆整体结构而言,平臂属于横向结构,而抱杆其他部分则为竖向结构,其相互之间存在着风效应干扰。
4 抱杆标准节风荷载的精细化计算
利用构件总计法原理[14],开展了抱杆标准节的风荷载精细化计算方法研究。构件总计法能够由单杆阻力系数推导得出格构式结构的整体体型系数。日本JEC-127—1979《送电用杆塔设计标准》(简称“JEC”)提出了构件总计法[14]。该法物理意义明确,与风洞试验结果吻合较好,与通过密实度计算的整体体型系数相比有更高的精度[15-17]。
构件总计法计算步骤为:1)基于杆件的截面形状及长细比计算出迎风面杆件的风荷载;2)基于迎风面和背风面构件的间隔距离计算出背风面杆件风荷载,继而进行总计;3)对杆件之间的风力干涉作用导致的影响进行修正,最后求出结果。除了标准节代表的正方形桁架之外,矩形桁架或桁架横担等的体型系数计算也均可采用此方法。
以图12标准节塔架为例,若该塔架节间的等效体型系数取为μc,则其可表示为[14]:
(6)
式中:μk为杆件k的体型系数;ηkf为杆件k迎风面干扰系数,以杆件迎风面风荷载与其无干扰下单根杆件体型系数之比表示;ηkb为杆件k背风面干扰系数,以杆件背风面风荷载与其无干扰下单根杆件体型系数之比表示;Ak为杆件k迎风面积。
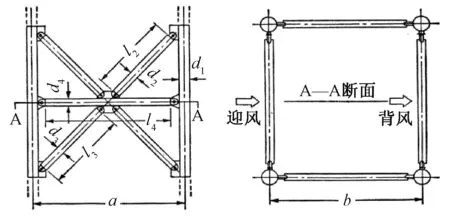
图12 对称塔架示意Fig.12 The schematic diagram of the symmetrical tower
同时定义塔架体型系数风洞试验值为μe并与式(6)得到的等效体型系数μc相比即为立体风力干涉系数K=μe/μc:
(7)
如果已知不同工况下单根杆件体型系数μk、干扰系数ηk以及立体风力干涉系数K,即可以通过式(8)进行简便计算,获取与风洞试验结果相近的体型系数取值。
(8)
式中:μ为构件总计法计算所得的塔架节间体型系数。为方便设计应用并从保守角度出发,不同湍流度及雷诺数下前杆的干扰系数取1,重点考虑后杆受前杆负干扰效应而导致体型系数增大的情形。由此式(8)即可简化为式(9)[14],其中ηk即为后杆的干扰系数,后文中统称为干扰系数。
(9)
其中μk=γμk∝
式中:γ为长细比修正系数,用以修正长细比对其体型系数的影响;μk∝为无限长二维流圆杆体型系数。
赵夏双针对不同长细比杆件模型及不同间距的双杆模型开展了相应的风洞试验并总结出均匀层流场(湍流度Iu=0)下杆件体型系数μk∝、长细比修正系数γ以及背风面荷载降低系数ηk的推荐公式[17],各系数取值如下:
(10a)
(10b)
ηk=-2.20/m+0.99ηk≤1
(10c)
其中m=S/D
式中:λ为杆件长细比;m为间距比;S为前后杆件间距;D为杆件直径。
根据K=μe/μc及式(5)不同风向角下标准节体型系数变化公式可得:
(11)
0°风向角下,基于式(9)、式(10)计算得到标准节等效体型系数μc=2.01。由此得到不同风向角下标准节立体风力干涉系数K(θ)计算公式:
(12)
由此基于μ(θ)=μcK(θ)即可得到基于构件总计法的不同风向角下塔架标准节体型系数。由于构件总计法物理意义明确,因此不同型号的抱杆塔身可通过式(9)、式(10)计算μc并结合式(11)来快速获取相对准确的各风向角体型系数。
此外,构件总计法可推广至抱杆平臂等复杂结构风荷载的精细化计算。构件总计法在计算抱杆构件体型系数的同时还可对关键部位杆件进行验算,以提高抱杆安全系数及优化抱杆用钢量。
5 结 论
以在建的凤城—梅里500 kV线路长江大跨越工程385 m高跨越塔为工程背景,开展了超大型组塔双平臂抱杆的风洞试验研究,为重大工程施工期抗风安全提供了保障。相关结论如下:
1)风洞试验结果表明抱杆标准节整体体型系数在各风向角下的变化存在线性规律,并得到了标准节体型系数随风向角变化的拟合公式。
2)通过对比风洞试验与《标准》所得抱杆结构整体风力系数发现:试验所得x向风力系数与《标准》较为接近,且结果略大于《标准》取值;试验所得y向风力系数与《标准》取值差异较大,主要在于《标准》简化取值无法全面考虑塔顶与平臂之间的干扰效应;抱杆整体结构体型系数的《标准》取值会偏于风险,应在抗风设计验算时予以重视,体型系数取值应结合风洞试验结果综合考虑。
3)基于风洞试验结果,并结合构件总计法,得到了不同风向角下抱杆标准节立体干涉风力系数计算公式。对于不同型号的抱杆塔身,可基于文中方法的简化公式(6)来快速获取相对准确的体型系数。
