基于Q-con非球面的折反射式全景光学系统设计

包晟，刘智颖，黄蕴涵，张禛

（长春理工大学 光电工程学院 光电测控与光信息传输技术教育部重点实验室，长春 130022）

0 引言

折反射式全景成像系统，最早是由SRINIVASAN M V 与Chahl J S 共同提出，在传统光学系统中添加反射镜用于获得全景成像［1］。折反射式全景成像系统的成像方式不同于传统光学系统遵从中心投影法，而是采用平面圆柱投影法，将位于围绕光学系统光轴360°范围内、垂直视场一定角度内的物通过反射镜及中继系统成像到二维平面上的圆环区域［2-3］。由于折反射式全景成像系统具有结构形式简单、视场宽广、畸变较小、成本较低等优势，同时能给人们带来全新的视觉体验和交互感知，从而广泛应用于医疗卫生［4］、无人机遥感［5］、勘测［6］等领域。

早期的反射镜面型单一，仅有球面、圆锥面、抛物面、双曲面等等，存在着视场较小、像质较差、反射镜口径较大、结构较复杂等问题，但是随着折反射式全景成像系统的发展，对于系统简易化与紧凑化有了更高的要求，而达到更高要求一般从反射镜的面型选择出发。相对于球面，非球面可以提供更多的自由度，具有显著的优势。同时由于单点金刚石车削技术的出现使得非球面的加工不再像以往那样困难，于是许多新的面型描述方法引入光学设计领域，比如非均匀有理B 样条、Zernike 多项式［7-8］、XY 多项式、径向基函数［9］、Q-type 多项式［10］和Bernstein［11］多项式等。其中近年来提出的Q-type 非球面引入的斜率约束可以使得非球面易于检测，在设计的同时可以给予加工评价，有利于提高加工效率和检测精度［12］，近年来已被成功应用于鱼眼镜头和全景环带镜头［13］等设计中，并获得很好的设计结果，有效的提升了镜头良率。目前鲜有将Q-type 非球面应用于折反射式全景光学系统设计的有关报道。

本文介绍了Q-type 非球面中的Q-con 非球面，首先确定初始二次曲面反射镜单元模型，并用Q-con 非球面进行拟合替换，再将Q-con 非球面转化为偶次非球面，对比了Q-con 非球面与偶次非球面的参数。最后为了进一步分析Q-con 面型与偶次非球面面型，实际设计了一款与Q-con 非球面折反射式全景系统具有相同参数的偶次非球面折反射式全景系统，结果表明，相对于偶次非球面，采用Q-con 非球面不仅可以提高系统设计效率、加工精度、减小成本，也可以实现畸变更小、像质更高、口径更小的设计结果，体现了将Q-con非球面应用于折反射式全景系统中的优势。

1 Q-con 非球面

幂级数非球面一直以来都是光学领域特别是光学设计领域中最广泛使用的，该面型表达式形式简单、使用方便。但是由于其各项系数之间非正交，尤其在应用高次项系数时，各项系数之间的相互干扰甚至抵消以及系数数量级严重偏小导致光学系统优化效率低下的问题更加突出。2007年，美国的FORBES G W博士提出了一种新型的函数多项式，具体可分为Q-con 型函数多项式（强效型）、Q-bfs 型函数多项式（温和型）与Q-bfs 扩展函数多项式三种表达形式［14-16］，光学领域将其统称为Q-type 函数多项式。这三种函数多项式的优点是表达式中各项偏离基准曲面系数项相互正交，克服了传统幂级数非球面表达式由于各项系数非正交带来的冗余干扰及精度缺失，提高了光学系统的优化设计效率，有利于得到更高质量的设计结果，并且对于加工和检测的难度没有加大。

本文选择Q-con 型非球面进行研究设计，Q-con 型函数多项式是在二次曲面的基础上加上新型多项式构造的，其表征非球面的矢高表达式为

式中，{ρ，θ，z}为圆柱坐标系坐标，c为非球面近轴处曲率半径，ρ为曲面某点到曲面轴心的距离，ρmax为曲面最大口径处到曲面轴心的距离，ρ2=x2+y2，取值范围为0 ≤ρ≤ρmax，k为圆锥系数，新型多项式Dcon(ρ/ρmax)为Q-con 非球面表达式与对应基准二次曲面的偏离，表达式为

式中，u为归一化坐标，−1 ≤u=ρ/ρmax≤1，am为对应的正交多项式系数，Qconm(x) 为正交多项式集｛Qconm(x)；m=0，1，…，M｝，既要满足式（1）使其能够更加准确的描述一个曲面面型，同时也要满足在求解正交项系数时能够最大程度的避免出现数值病态。

对于任意的曲面z=f(ρ)，其与式（1）中的二次曲面的差异即为多次项g(ρ)，将其与（1）式中的多次项进行拟合

进行拟合的过程就是令E2(a1，a2，…，am)的梯度等于0 的过程，式（3）尖括号表示对括号内函数的积分或和的加权平均，此时会得到最优化表达式

由格拉姆矩阵（Gram matrix）的性质得知Gmn为格拉姆矩阵，所以Gmn也是一个半正定的对称矩阵。为了避免曲面拟合时数值病态，出现错误，需要将格拉姆矩阵正交从而转化为对角矩阵，因为对角矩阵的性质为主对角线之外的元素均为0而其余元素不全为0，于是将式（5）构造为如式（6）所示结果从而转化成一个对角矩阵。

又有，雅可比（Jacobi）多项式(x)是在（−1，1）上关于权函数组成正交多项式，有

对比式（6）与式（7），发现两式结构类似，为了让两式能够相互转化，于是将（7）式进行改造，将其积分上下限变换为0～1，变换结果为

再将式（6）与式（8）进行对比，（1−x）次方值为0，x的次方值为4，于是得出α=0，β=4，又有Qconm(x)=(2x−1)，所以(x)推导的最终表达式为

对于(x)的计算，其为特殊的雅可比多项式，于是可以通过计算对应的雅可比多项式(x)而得出，于是有

式中，α=0，β=4，令权函数w(x)=(1 −x)α(1+x)β为零，于是通过计算，前六项可写为

尽管当式（3）的均方根误差计算为一个有限和，基底（10）仍然为一个良好的选择，虽然Gram 矩阵可能不是一个完全精确的对角矩阵，但是其仍能通过保持良好的数值对各项进行约束限制，进而避免数值病态的发生。

综上所述，Q-con 函数多项式的基底多项式相互正交，避免了非正交带来的冗余干扰、精度缺失与数值病态的问题，并且提供了更多的有效数字，提高了光学系统的优化设计效率及可加工性。因此本文将Q-con 非球面应用于折反射式全景光学系统的反射镜单元，以提高系统设计效率的同时获得成像质量更高的设计结果。

2 光学系统设计

2.1 光学系统设计参数

设计的折反射式全景光学系统根据使用要求，光谱范围为可见光波段，视场角为（65°～115°）×360°，拟采用1/1.6 inch CMOS 传感器接收，传感器有效像面尺寸为8 mm×6 mm，像元尺寸5.4 μm×5.4 μm。依据等距投影的映射原理，通过目标视场以及CMOS 传感器尺寸大小，再考虑f-θ畸变，将焦距目标值设置为1.24 mm，具体设计指标参数见表1。

表1 折反射式全景光学系统设计参数Table 1 Specifications of the catadioptric panoramic optical system

2.2 折反射式全景系统尺寸的确定

折反射式全景成像系统主要包括反射镜单元、中继系统、CCD，其中反射镜单元起到扩大系统成像视场的作用，能够将光线转入到后面的中继系统中，进而实现视场角大于180°的全景成像。其系统尺寸主要由中继系统到反射镜单元最大口径处的轴向距离h和反射镜单元口径D所决定。如图1 所示为折反射式全景光学系统的尺寸关系，其中虚线表示该光学系统最大视场的主光线，该系统相对于光轴旋转对称。图中y为系统的全像高，f为中继系统焦距，光线通过反射镜压缩后视场角为θ。则有

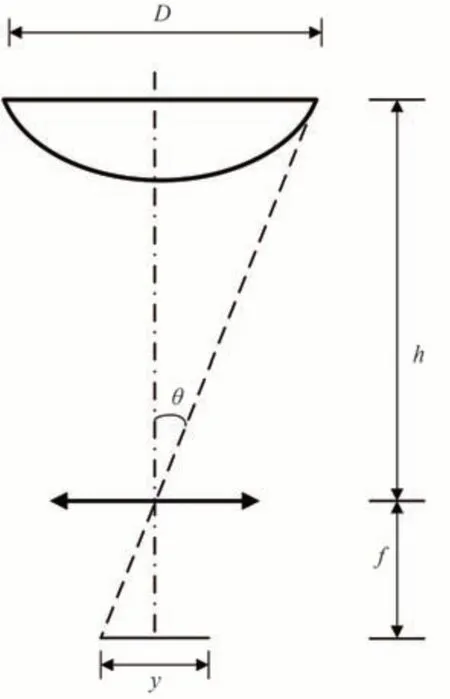
图1 折反射全景成像系统的尺寸关系Fig.1 Calculating size of catadioptric panoramic optical system

式（12）即为该折反射式全景成像系统的系统口径、中继系统视场角与靶面尺寸之间的关系，设计时根据实际应用选择合适的视场角θ、中继系统焦距f及全像高，并确定合理的反射镜口径D和中继系统到反射镜单元最大口径处的轴向距离h。

2.3 反射镜单元初始结构建模

对反射镜单元进行初始结构建模的过程中首先要知道其光线走向，大视场光线通过反射镜反射折转进入中继系统中，中继系统将光线会聚到靶面上。折反射式全景光学系统由中继系统校正场曲，所以在反射镜单元建立的过程中，不考虑场曲的校正，设计时将像面弯曲，在中继系统设计时让像面反方向弯曲，从而让反射镜单元与中继系统的匹兹伐场曲相互抵消从而达到校正场曲的目的，即有

式中，PRelay为中继系统的匹兹伐和，Pmirror为反射镜单元的匹兹伐和，对于含有多个光学表面的光学系统而言，其匹兹伐和可以写为

式中，J是拉氏不变量，ni和n′i分别是表面前后介质的折射率，ci是此面的曲率半径。由于反射镜单元前后介质均为空气，折射率为1，所以反射镜单元的匹兹伐和为

在反射镜单元会产生场曲的情况下，在反射镜单元建模时应将像面弯曲设计，曲率半径为匹兹伐半径，来保证之后整体的场曲补偿。为了实现建模整体性，在进行反射镜单元建模时使用近轴透镜代替中继系统，并将光阑设置在近轴透镜前。建模后的反射镜初始结构如图2 所示。

图2 反射镜单元初始结构建模结果Fig.2 The results of modeling the initial structure of the mirror element

2.4 反射镜单元的Q-con 非球面的拟合替换与优化

初始结构设计完成后，需要将反射镜二次曲面面型拟合为Q-con 非球面。光线在二次曲面反射镜单元反射时的半口径值Y坐标范围为9.75 mm～26.75 mm。通过ZEMAX 将反射镜单元面型替换为Q-con 面型后优化，光线在Q-con 非球面反射镜单元反射时的半口径值Y坐标范围为9.75 mm～26.25 mm。ZEMAX软件中SSAG 操作数可以获取任意表面在半口径值Y坐标下对应的矢高值（Saggital depth，SAG），为了获得二次曲面反射镜单元及Q-con 非球面反射镜单元面型曲线，将半口径Y值步长设置为0.25 mm，得到反射镜单元在半口径值Y坐标下对应的矢高值。将数据导出并以曲线图表示如图3 所示。

图3 二次曲面面型及Q-con 非球面面型的反射镜单元的Y-SAG 曲线Fig.3 H-SAG curves of mirror elements with quadratic surface and Q-con aspheric surface

图4 曲面拟合结果Fig.4 The results of surface fitting.

完成反射镜单元Q-con 非球面的优化与拟合后，将得到的反射镜面型替换为拟合后的Q-con 曲面，替换后的Q-con 反射镜单元点列图、调制传递函数曲线图如图5 所示。Q-con 反射镜单元不考虑场曲的校正，因此其场曲大小可以由像方弯曲程度所体现，该反射镜单元像面半径为10.218 mm。

图5 Q-con 非球面反射镜单元成像性能Fig.5 Performances of Q-con aspheric mirror element

2.5 中继系统的设计

完成反射镜单元设计后，对中继系统的设计进行分析。中继系统的作用是收集反射镜反射的光线会聚到靶面上。由于反射镜单元与中继系统分别设计，最后拼接，所以依据光瞳衔接原则，反射镜单元的出瞳等于中继系统的入瞳，同时将光阑放置在中继系统的最前侧。反射镜单元出瞳直径Dmirror为3 mm，所以中继系统入瞳直径Drelay也设置为3 mm。同时通过Q-con 非球面反射镜单元初始结构建模得知，近轴面焦距fparaxial为9 mm，所以中继系统焦距也为9 mm。再通过像距l′、近轴面口径D、以及近轴面焦距fparaxial可以计算出NAparaxial=0.018 93 后，中继系统物方NArelay大小需要与NAparaxial相同，有如下关系式

中继系统的设计除了满足式（16），匹兹伐场曲还需要满足式（13），即中继系统的像面弯曲要与反射镜设计的像面弯曲大小相等，方向相反，从而使得匹兹伐场曲相互抵消，得到校正。

从像差理论出发，根据消色差原理以及合理的光焦度分配，决定采用经典的H-ZF1、ZK9B，H-ZK9B、ZF7L 消色差玻璃组合，以及低折射率低色散玻璃材料H-FK71 进一步消色差。经过反复的修改优化，最终的中继系统设计结果如图6 所示。点列图、调制传递函数曲线图如图7 所示。

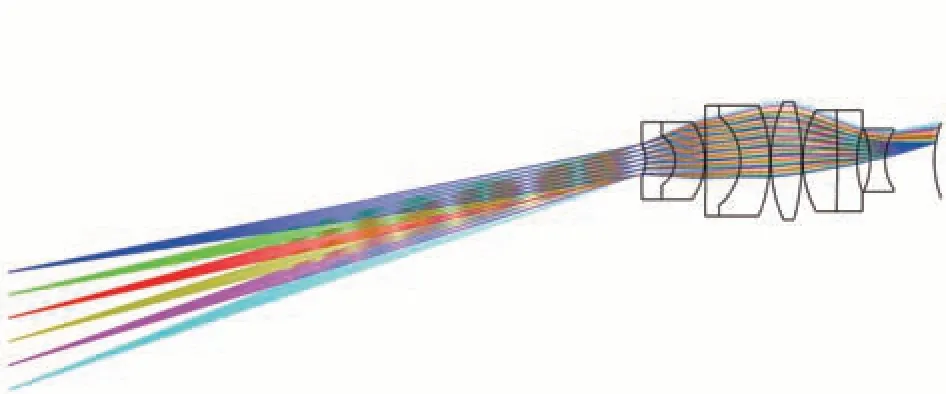
图6 中继系统设计结果Fig.6 Design results of relay system

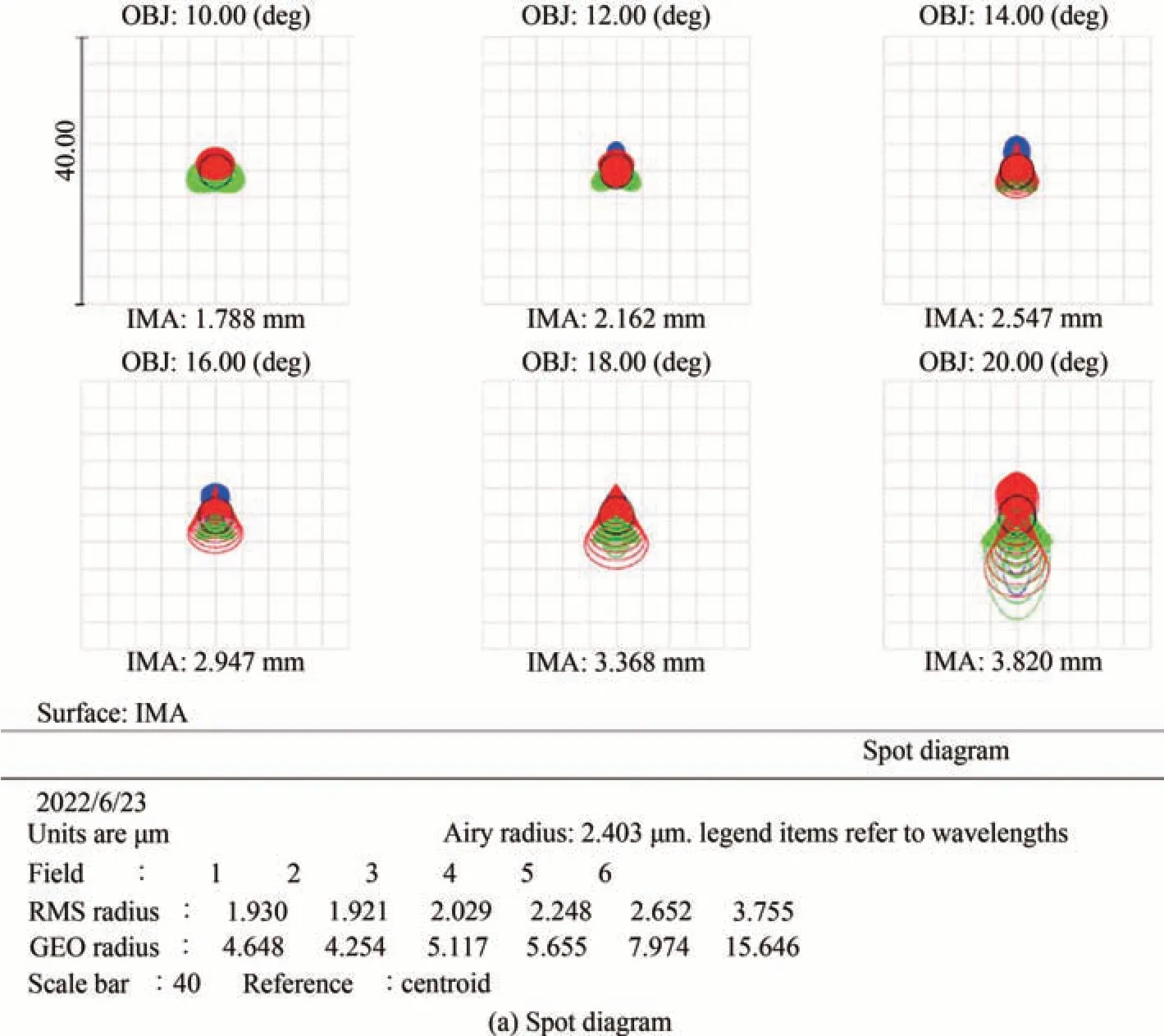
图7 中继系统成像性能Fig.7 Performances of relay system

3 折反射式全景成像系统设计结果与分析

将反射镜单元与中继系统进行拼接，拼接后的折反射式全景成像系统点列图、调制传递函数曲线图及场曲和畸变曲线如图8 所示。

图8 拼接后系统成像性能Fig.8 Performances after system splicing

可以看到，拼接后像质虽然有所下降，但是场曲相互抵消得到校正，其小于±0.1 mm 范围内。为了提高像质，满足设计指标要求，在此基础上对该光学系统进一步优化，为了提高优化效率令透镜厚度保持不变，限制中继系统结构与总长不产生过大变化。再通过TTHI、MNEG、MNCA 等操作数对中继系统间距及边缘厚度进行限制，使得透镜在合理的可加工及装配的范围之内。

通过反复的调整与优化，得到了视场为（65°～115°）×360°，可见光波段，焦距为1.24 mm，F数为3.5，光学系统总长度为99.8 mm，后截距为5 mm 的折反射式全景成像光学系统。系统光学系统结构如图9（a）所示，折反射式全景成像系统中反射镜单元面型为Q-con 型非球面，中继系统由三个双胶合透镜、一个场镜、一个正透镜组成来校正像差。该系统反射镜单元极大的扩大了系统的视场角，同时根据光学设计手册得知，镜组的最小中心厚度以及边缘厚度、边厚比、D/R等均在合理的可加工的范围之内。图9（b）是该折反射式全景系统的环带像面示意图，环带内径为1.318 mm，环带外径2.935 mm，盲区面积占大圆面积20%左右，传感器像元利用率较高。

现代社会，人们在文化习俗、道德理念、价值观念以及行为方式等方面普遍而深刻地存在着差异、分歧和冲突。这些差异、分歧、冲突并没有明确有效的方式使其趋于融合。文化习俗、道德理念、价值观念以及行为方式的多元性意味着存在多种合理的价值以及关于共同的善的合理观念。社会各阶层可以自由地采纳其中一种价值观念，或是从某种利益出发把不同的价值结合在一起，还可以自由地形成本阶层关于良善生活的观念。“不同的生活方式崇尚不同的善和德性这一事实并非不完美的特征，而是人类可以以不同的生活方式很好地生活的标志”。[12]

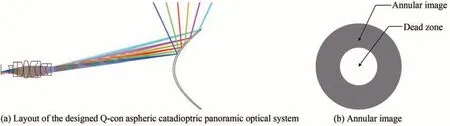
图9 设计结果Fig.9 Design result

图10（a）为折反射式全景系统的点列图，可以看到全视场范围内均方根弥散斑半径为2.093 μm，小于艾里斑半径2.58 μm；图10（b）为系统的调制传递函数曲线图，在尼奎斯特空间频率93l p/mm 处，最大视场调制传递函数大于0.4，其余视场均大于0.5，接近衍射极限；图10（c）为系统的场曲和畸变曲线，可以看到，该系统最大畸变小于12%。

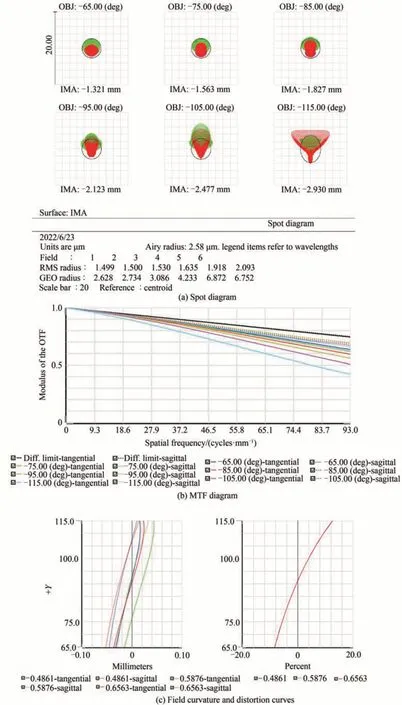
图10 Q-con 非球面折反射式全景系统成像性能Fig.10 Performances of the designed Q-con aspheric catadioptric panoramic optical system

通过ZEMAX 的Surface Conversion Tool 将反射镜单元Q-con 非球面转换为最高级次为14 次的偶次非球面，使其与Q-con 非球面多项式级次相等。反射镜单元Q-con 表达式中的全部8 个参数和转化后的偶次非球面表达式的8 个参数如表2。

表2 反射镜单元Q-con 非球面参数与对应的偶次非球面参数Table 2 Parameters of the designed mirror element Q-con aspheres and corresponding even aspheres

由表可以看出Q-con 多项式系数am（a0～a5）的数量级在10−5以内；而转换后的偶次非球面多项式系数a4～a14数量级达到了10−21，比对应的Q-con 多项式系数小5～16 个数量级，这表明了在同样的的计算平台下，Q-con 多项式系数具有更大的数量级，可以保留更多的有效数字。

进一步对比两种非球面面型，从共同的初始结构模型出发，采用与Q-con 非球面面型的反射镜单元相近的结构设计了偶次非球面面型的反射镜单元。系统中使用的透镜材料、数量、位置均与Q-con 折反射式全景成像系统相同，最终设计的反射镜单元偶次非球面面型数据如表3 所示。从表中数据可知，偶次非球面系数数量级10−6～10−22，比对应的Q-con 多项式系数小5～17 个数量级，验证了表二的分析结果。

表3 反射镜单元偶次非球面面型参数Table 3 Parameters of the designed mirror element even aspheres

一方面，相对于传统的偶次非球面表达式，Q-con 非球面表达式可以保留更多的有效数字从而提高光学元件可加工性与加工精度。另一方面，由于Q-con 多项式各系数项互相正交，避免了传统偶次非球面各项系数相互影响的弱点从而可以提高优化效率，所以采用Q-con 非球面进行优化设计可以在达到更高像质的同时也具有更高的可加工性。

为了更直观的对比两种面型的可加工性，采用反射镜单元面型与其基准二次曲面面型的矢高偏离程度作为衡量加工难易程度的评价指标，计算了两种面型与其基准二次曲面之间的矢高偏离量。如图11 所示即为Q-con 非球面和偶次非球面与其基准二次曲面的矢高偏离量。可以看到Q-con 非球面的矢高偏移量最大为250 μm，而偶次非球面的矢高偏移量最大为806 μm，是Q-con 非球面矢高偏移量最大值的三倍以上。说明采用Q-con 非球面的反射镜单元具有更好的可加工性。

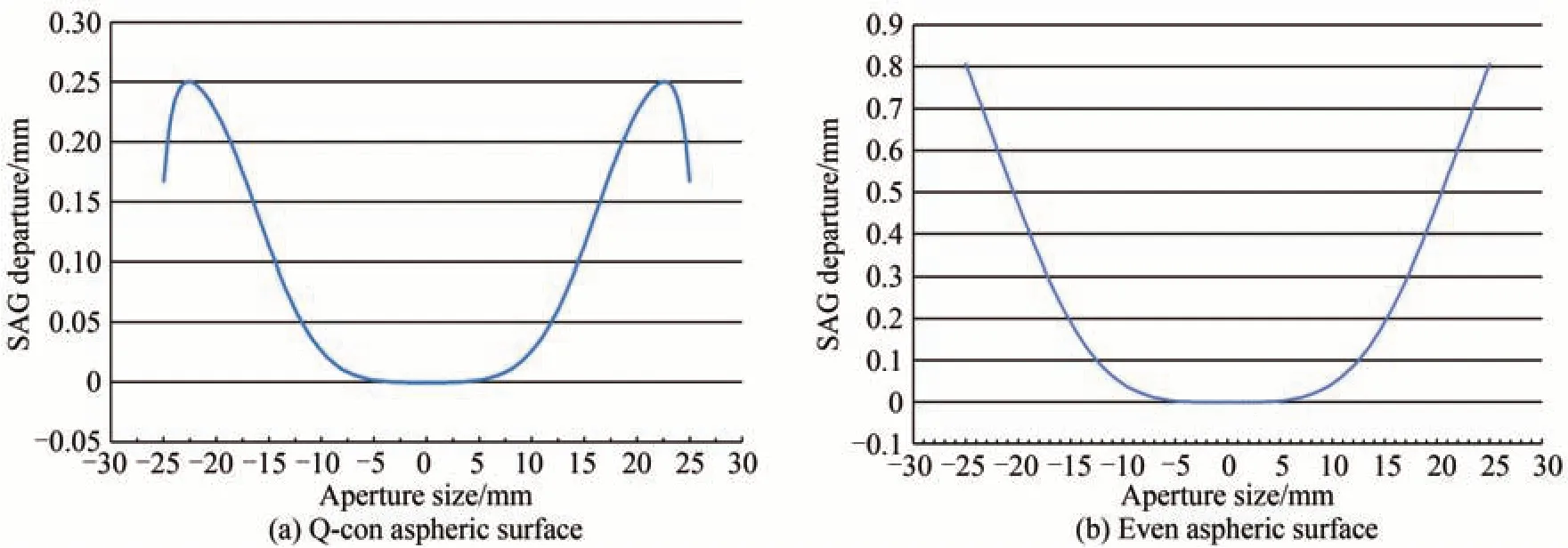
图11 矢高偏离量Fig.11 SAG departure

图12（a）为折反射式全景系统的点列图，可以看到在全视场范围内均方根弥散斑半径为2.675 μm，比Q-con 非球面设计的弥散斑半径2.093 μm 高出27.8%；图12（b）为系统的调制传递函数曲线图，在尼奎斯特空间频率93l p/mm 处，最大视场调制传递函数接近0.4，其余视场均大于0.5，略低于Q-con 非球面设计结果；图12（c）为系统的场曲和畸变曲线，可以看到，该系统最大畸变15%，比Q-con 非球面设计的畸变12%高出25%；同时该反射镜单元尺寸50 mm，比Q-con 非球面设计的反射镜单元尺寸45 mm 高出11.1%。综上所述，采用Q-con 非球面面型在提高系统的设计效率、加工精度、减小成本的同时也可以实现畸变更小、像质更高、口径更小的设计结果。

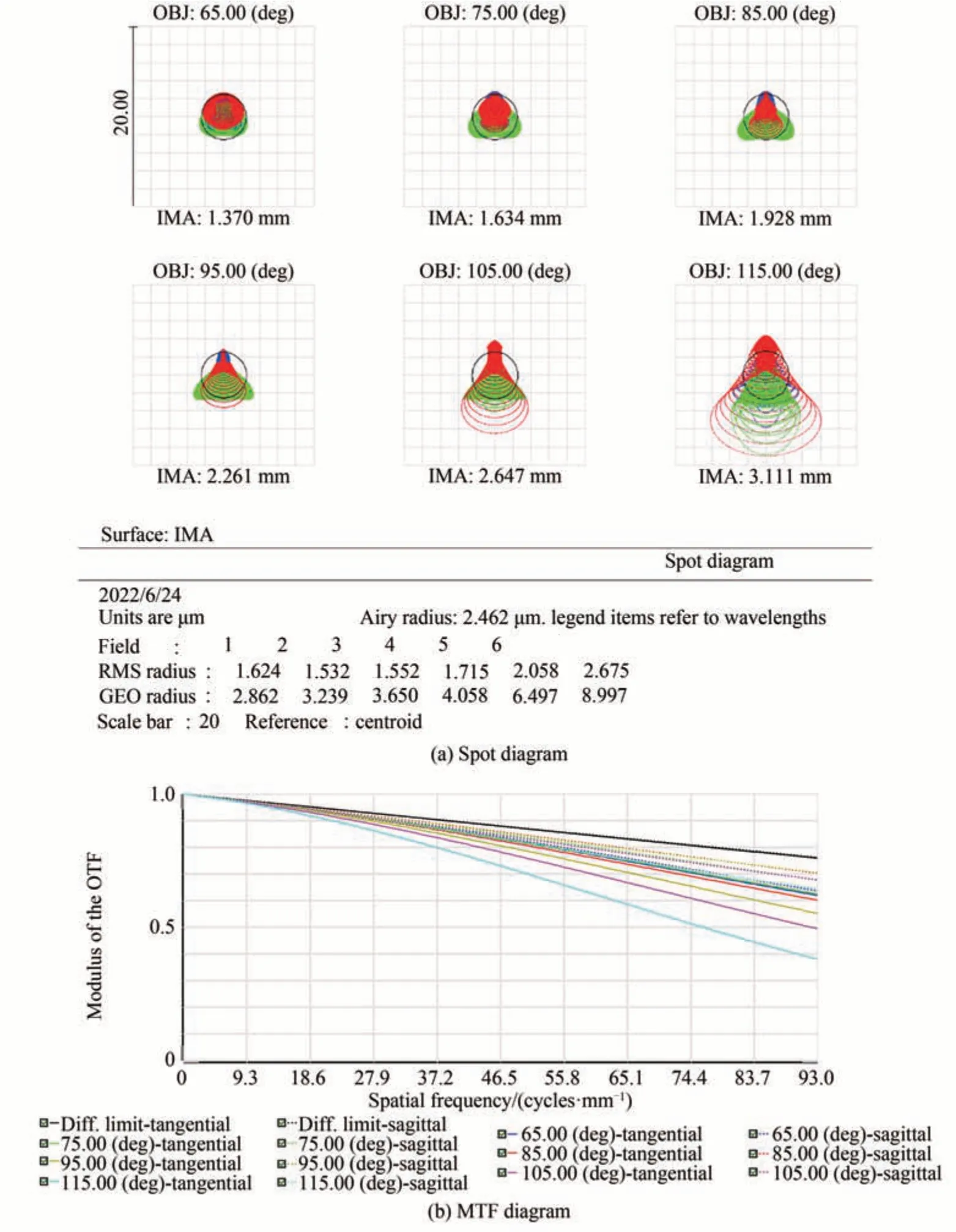
图12 偶次非球面折反射式全景系统成像性能Fig.12 Performances of the designed even aspheric catadioptric panoramic optical system

4 结论

利用Q-con 非球面设计了一款可见光工作波段，视场大小为（65°～115°）×360°，焦距为1.24 mm，F数为3.5，总长为100 mm 的折反射式全景成像系统。该系统反射镜单元采用Q-con 非球面面型，成像质量接近衍射极限。将Q-con 非球面转化为偶次非球面，表明了Q-con 非球面系数相对于偶次非球面系数具有更大的数量级，可以保留更多的有效数字。最后，为了进一步对比Q-con 面型与偶次非球面面型，实际设计了一款与Q-con 非球面折反射式全景系统具有相同参数的偶次非球面折反射式全景系统，对两者进行了分析比较。结果表明，相对于偶次非球面，采用Q-con 非球面不仅可以提高系统设计效率、加工精度、减小成本，也可以实现畸变更小、像质更高、口径更小的设计结果。